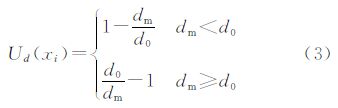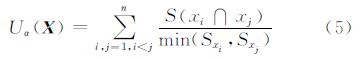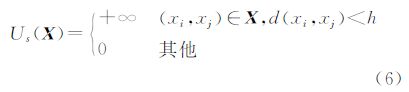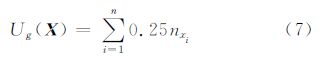2. 武汉大学 时空数据智能获取技术与应用教育部工程研究中心,湖北 武汉 430079
2. Engineering Research Center for Spatio-Temporal Data Smart Acquisition and Application, Ministry of Education of China, Wuhan University, Wuhan 430079, China
激光扫描测量是近十几年快速发展的一种新型测量技术,在三维城市建模、植被检测、通信线路设计、城市规划和灾害处理等领域都有广泛的应用前景[1],现已逐渐成为三维城市数据模型获取的一种重要方法。建筑物、道路和树冠是城市空间中最主要、最重要的空间实体,其三维信息是重要的基础地理信息。因此建筑物和树冠的目标提取对于城市制图和三维建模也就具有极大的研究和实用价值[2]。
近年来,国内外对基于LiDAR数据的建筑物目标提取进行了广泛的研究。主要可以分为两类:一类方法是只使用LiDAR数据提取建筑物目标[3];另一类方法是融合LiDAR数据与IKONOS影像[4]、航空影像[5]以及其他遥感影像或地面规划设计图[6]来提取建筑物。第1类方法,首先根据LiDAR数据得到DSM和DEM,然后利用两者之差分离出地面点和非地面点,最后从非地面点中进一步提取感兴趣的建筑物目标点云。这类方法的缺点是当地形较复杂时生成的DEM精度较差,从而影响最终的提取结果。第2类方法是融合LiDAR数据与IKONOS影像[4]、航空影像[5]以及其他遥感影像或地面规划设计图[6]来提取建筑物。这类方法可以降低处理难度,但是对数据的同时获取提出了更高的要求,并且地面规划设计图对新建房屋不能及时处理[7]。
在目标提取问题中,引入空间信息和空间关系可以显著提高算法的准确性和可靠性。一种引入空间信息和空间关系的有效方法是使用统计几何方法。该方法通过先验模型引入空间特性。这类方法中的一个主要模型是马尔可夫随机场 (MRF)。MRF在很多问题中都得到了较好的效果[8]。但MRF是一种基于像素级随机场的分析方法,对噪声较敏感,且容易陷入局部最小值。而标记点过程是一种基于高层随机场的分析方法,可以很好的解决这些问题,该方法是一种面向对象的统计几何方法。标记点过程方法根据目标的几何特征建立吉布斯自由能变模型,通过目标的一致性建立该模型的数据项,通过目标的拓扑性质等空间特性建立该模型的先验项,然后利用可逆跳转马尔可夫蒙特卡洛算法(RJMCMC)进行采样,并采用模拟退火算法进行优化求解[9]。近年来,基于标记点过程的方法已被广泛用于高分辨率影像处理中,并取得了较好的效果。文献[10, 11]都使用标记点过程方法从DEM中提取建筑物目标。但是,文献[10]的方法参数设置复杂,针对不同的数据,需要对每一个参数进行调试,处理起来非常麻烦。文献[11]则使用目标边缘的梯度信息作为吉布斯自由能变模型的数据项,但当目标的边缘不明显或与其他目标紧密相连时提取结果较差。文献[12]在文献[10]研究的基础上,利用基于标记点过程的方法从DEM数据中进行建筑物三维重建。文献[9]利用标记点过程进行车道线的识别和提取。文献[13]采用标记点过程方法用椭圆模型进行树冠提取,从而统计森林中的树木数量。 但该方法需要对遥感影像进行预处理,把遥感影像转化为二值影像。文献[14]对直线、矩形和圆等模型进行综合,提出基于多标记点过程的目标提取方法,它包括7种随机模型,能适应多种应用,如计数统计,纹理表达,路网提取等。但该方法中吉布斯自由能变模型的参数设置范围较大,调试较困难。
由于激光扫描获取的点云数据量大,难以直接对点云的几何数据进行分类和特征提取。故本文将机载激光扫描点云数据转换成点云特征影像,针对激光扫描数据生成点云特征影像的算法已经比较成熟[15, 16],采用文献[16]中的方法生成点云特征影像,提出基于多标记点过程的建筑物和树冠目标对象的自动提取方法。该方法首先根据目标的几何特征建立吉布斯自由能变模型,通过目标的一致性建立该模型的数据项,通过目标的拓扑性质等空间特性建立该模型的先验项,然后利用RJMCMC算法采样,并采用模拟退火算法进行优化求解,实现建筑物目标和树冠目标几何对象的多目标自动提取,并同时得到建筑物和树木的数量、中心点位置、目标的大小以及目标的方向角等信息。本文算法流程图见图 1。
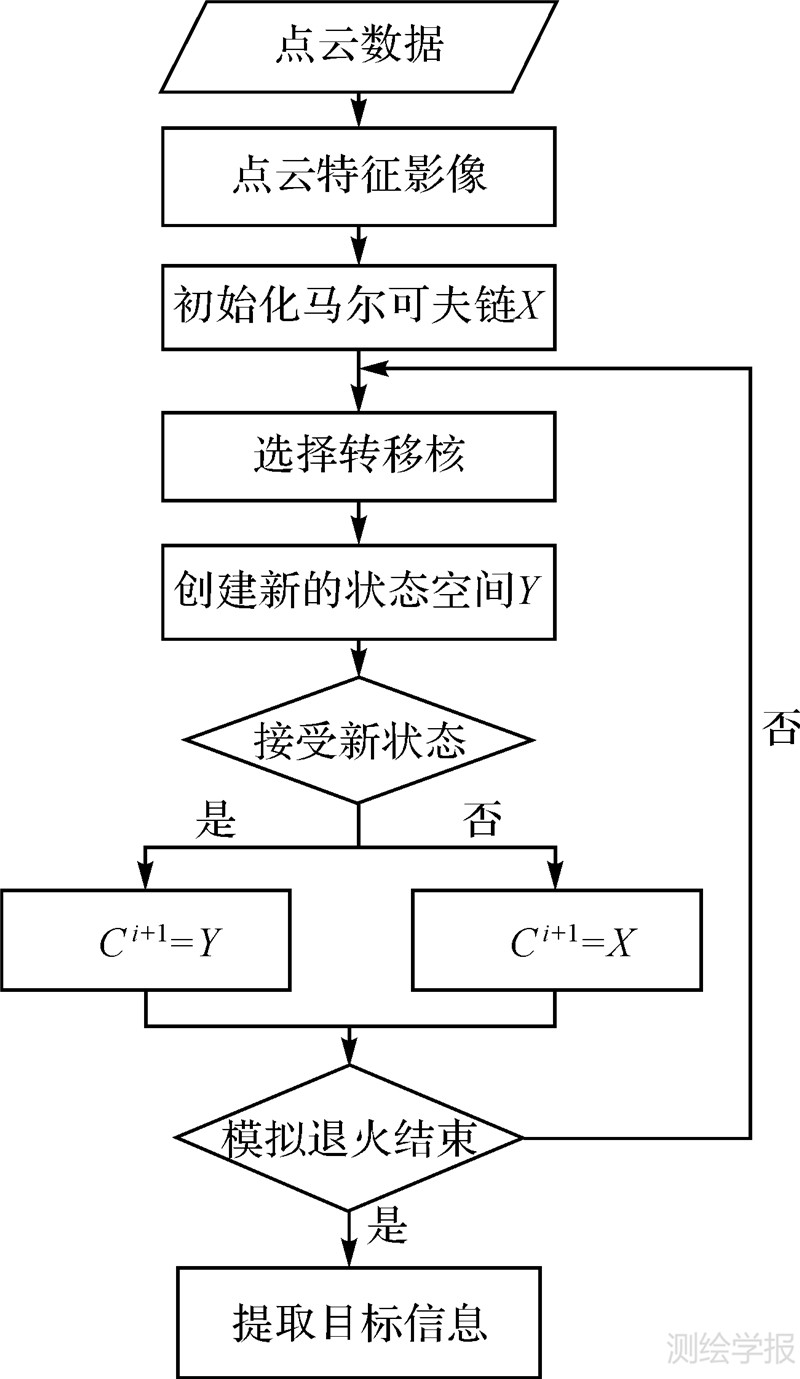
|
| 图 1 目标提取流程图 Fig. 1 The flow chart of object extraction based on marked point process |
在广泛应用于图像分析的随机方法中,标记点过程具有组合全局信息来识别几何形状的优点,该方法是一种面向对象的统计几何方法。一个按一定统计规律在某空间中随机分布的点集就形成一个随机点过程(简称点过程)。随机点过程是描述随机点分布的随机过程[17]。 标记点过程就是带有辅助变量的点过程,这个辅助变量即为联系于每一点的标记。
对点云特征影像上的建筑物、树木等不同目标的提取过程可以看做随机过程(空间点过程)的一种--泊松过程(Poisson process)。需要处理的数据构成的有界区域组成一个框架空间Λ,一个定义在框架空间Λ上具有密度估计μ和密度函数ρ的泊松过程X满足[14]:对任意的有界区域B⊂R2,μ(B)>0,满足N(B)为均值为μ(B)的泊松分布;已知N(B),XB中的点相互独立,且密度与ρ(u),u∈B成比例。因此可利用具有强度ν(·)的齐次泊松分布和框架空间Λ上的非负函数h(·)定义概率密度测度μ(·):μ(B)=∫Bh(x)ν(dx)。
本文结合建筑物和树冠的形状,分别使用矩形和椭圆作为建筑物和树冠的标记(图 2)。
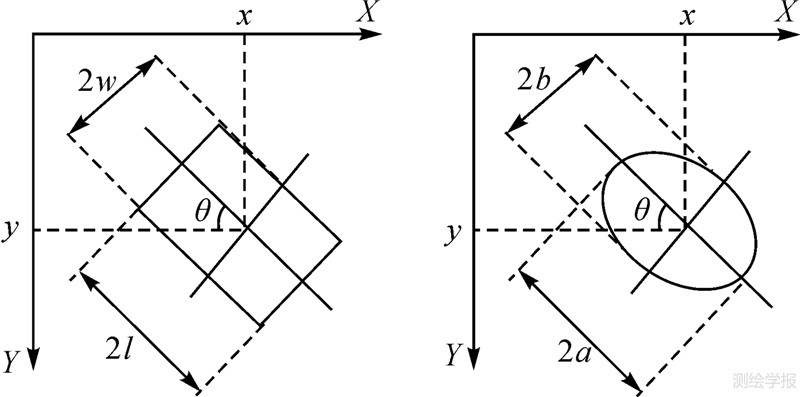
|
| 图 2 矩形和椭圆的位置和标记信息 Fig. 2 Position and marks of rectangle and ellipse |
矩形和椭圆的位置和标记信息如下
SEllipse=[0,xmax]×[0,ymax]×[amin,amax]×[bmin,bmax]×[0,π] a≥b

|
| 图 3 点过程和标记点过程 Fig. 3 A point process and a marked point process |
本文考虑提取目标的标记点过程符合Poisson分布,其概率密度为可以通过两种方式定义:一是在贝叶斯框架下,但是这种情况需要知道数据的DEM;二是通过吉布斯自由能变模型[11]。由于在复杂地形下获取数据的DEM比较困难,且精度较低,因此本文采用第2种方式,通过吉布斯自由能变模型U(X)说明点过程,吉布斯函数的测度定义为
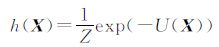
 是一个归一化常数,称为吉布斯配分函数[14]。全局吉布斯自由能变值通常被分解为局部自由能变值之和。为避免复杂的归一化常数的求解,本文采用RJMCMC算法和模拟退火算法求解函数的最优解。
是一个归一化常数,称为吉布斯配分函数[14]。全局吉布斯自由能变值通常被分解为局部自由能变值之和。为避免复杂的归一化常数的求解,本文采用RJMCMC算法和模拟退火算法求解函数的最优解。
对于吉布斯自由能变模型U(X),本文主要考虑数据一致性因子Ud(X)和先验约束因子Up(X)。
本文主要目的是提取建筑物轮廓,同时可以提取树冠轮廓。下面的说明皆以矩形目标为例,同理可得到对椭圆目标的操作。为均衡数据一致性因子和先验约束因子对吉布斯自由能变值的贡献,本文把各类因子的取值范围归一化到[-1, 1]之内。
3.1 数据一致性因子Ud(X)累积目标框架X中每个目标xi的局部吉布斯自由能变值
式中,Ud(xi)是目标xi的吉布斯自由能变模型的数据一致性因子。该因子满足目标之间相互独立且目标的吉布斯自由能变值具有负值两个重要条件[14]。本文认为目标内部区域具有一致性,与外部区域具有差异性。Ud(xi)定义为 式中,dm表示目标内部区域和外部区域之间的马氏距离,(min,σin)、(mout,σout)分别表示内部区域和外部区域的平均像素值和标准偏差;n1和n2分别表示内部区域和外部区域的面积(见图 4)。外部区域的宽度设置为固定值,一般根据影像的分辨率设置为2~4。马氏距离是一种有效的计算两个未知样本集的相似度的方法,它考虑到各种特性之间的联系,并且是尺度无关的。文献[18]使用巴氏距离建立吉布斯自由能变模型的数据一致性因子,但是当巴氏距离的第1项和第2项为同一数量级时,此计算方法会产生较大误差。阈值d0是模型唯一需要调试的参数,调节数据拟合的敏感性,控制吉布斯自由能变模型的数据一致性因子的取值。当矩形目标和特征影像中的目标匹配的较好时,吉布斯自由能变模型的数据一致性因子取值应为负值。

|
| 图 4 目标和数据的一致性测度 Fig. 4 Coherence measure between object and data |
Up(X)引入目标之间的交互作用和目标梯度等先验知识。本文限制目标间的重叠,建立适合非重叠目标的一般模型,并加入强结构信息。
每一区域只能有一种标记,对具有重叠区域的目标进行惩罚。定义两个重叠目标的惩罚因子的计算公式为(见图 5)
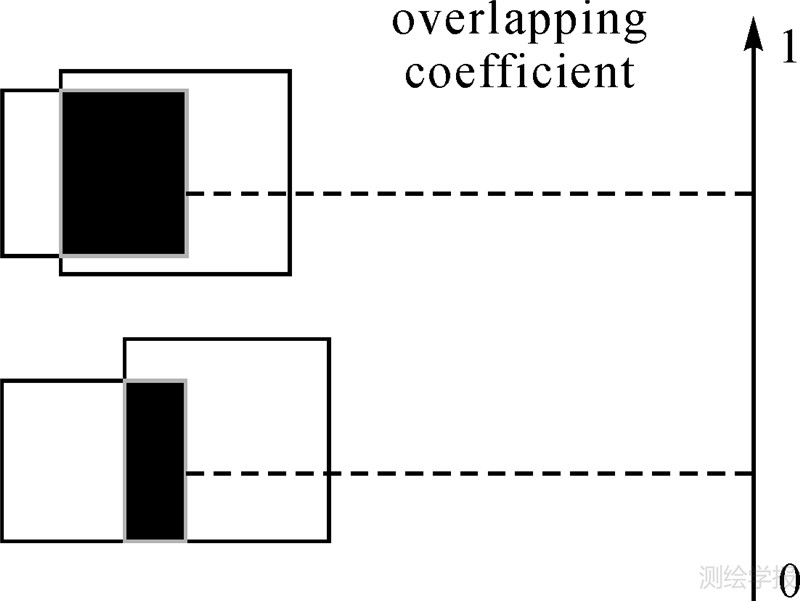
|
| 图 5 重叠目标的量化 Fig. 5 Two overlapping objects and the quality |
该先验知识能够体现目标之间的重叠关系,惩罚有重叠的目标,通过该因子可以对简单模型进行组合,从而提取复杂目标。
本文定义一个强制约束,对中心点距离非常近的目标赋予非常大的吉布斯自由能变值,以杜绝同一区域具有不同的标记。距离阈值h根据具体的数据确定(式6)。
考虑到目标的边缘梯度对目标的确定具有较大作用,本文加入梯度约束。对矩形每条边上的点搜索其八邻域,计算每个点与其八邻域内的点的灰度差的绝对值的最大值,把该值作为该点的灰度梯度值,当一条边的平均灰度梯度值小于一定阈值时对该目标进行惩罚。计算公式为
式中,nxi表示每个目标中小于给定灰度梯度阈值的边的数目。该梯度阈值可以通过生成目标的梯度图像提前确定,不需要进行反复调试。综上所述,计算吉布斯自由能变模型的先验因子的公式为
本算法的实质是求解吉布斯自由能变模型U(X)的全局最小能量,实现实体对象与点云数据的最佳匹配,从而识别出点云数据中蕴含的几何对象。该方法克服了传统方法只能得到局部最优的不足。本文采用RJMCMC算法进行采样,使用模拟退火算法进行优化[9]。下面对RJMCMC算法和模拟退火算法两个关键技术进行说明。
4.1 RJMCMC算法马尔可夫蒙特卡洛(MCMC)算法是一种简单且行之有效的贝叶斯计算方法,该迭代算法并不依赖于初始状态空间[9]。文献[19]提出了RJMCMC方法,该算法是一种特殊的Metropolis-Hastings算法,可以在不同维度之间可逆跳转,被广泛地应用于最大化问题。决定跳转的概率为计算得到的Green比。
RJMCMC算法对目标的参数进行修改,并且改变状态空间的大小。该算法令q(Y|X)为任意一个转移核,假设已经生成状态空间X0、X1、…、Xi,为了生成状态空间Xi+1,进行如下步骤:
(1) 产生一个转移核,并根据转移核得到新的状态空间Y~q(Y|Xi)。
(2) 计算Green比r=r(Xi,Y),其中

(3) 设定
对于接受率r(Xi,Y)的计算需保证该跳转是可逆跳转。实际上,转移核由不同建议的转移核组成,不同的转移核对应不同的Green比r(Xi,Y)。本文中各种转移核的Green比的计算见文献[13, 14, 19]。
为保证马尔可夫链可逆并收敛到最优解,本文采用7种转移核,分别为:生、灭、平移、旋转、缩放、分裂和合并。均匀生灭转移核保证马尔可夫链收敛到最优解,非跳跃变换转移核和分裂合并转移核加速马尔可夫链的收敛[9]。为加速马尔可夫链的收敛,本文对不同转移核的选择赋予不同的概率。实际中,一般对平移、旋转和缩放3种转移核赋予较大的概率[13]。
均匀生灭转移核是指在当前状态空间中随机添加或移除一个目标,这一变换对应于高维状态空间和低维状态空间之间的跳转。向高维跳转相当于生的过程,而向低维跳转则相当于灭的过程。图 6(a)中黑色目标表示在原来的状态空间中随机加入一个目标,该目标的位置和形状参数都是随机生成的,灰色目标则表示在原来的状态空间中随机的移除一个目标。
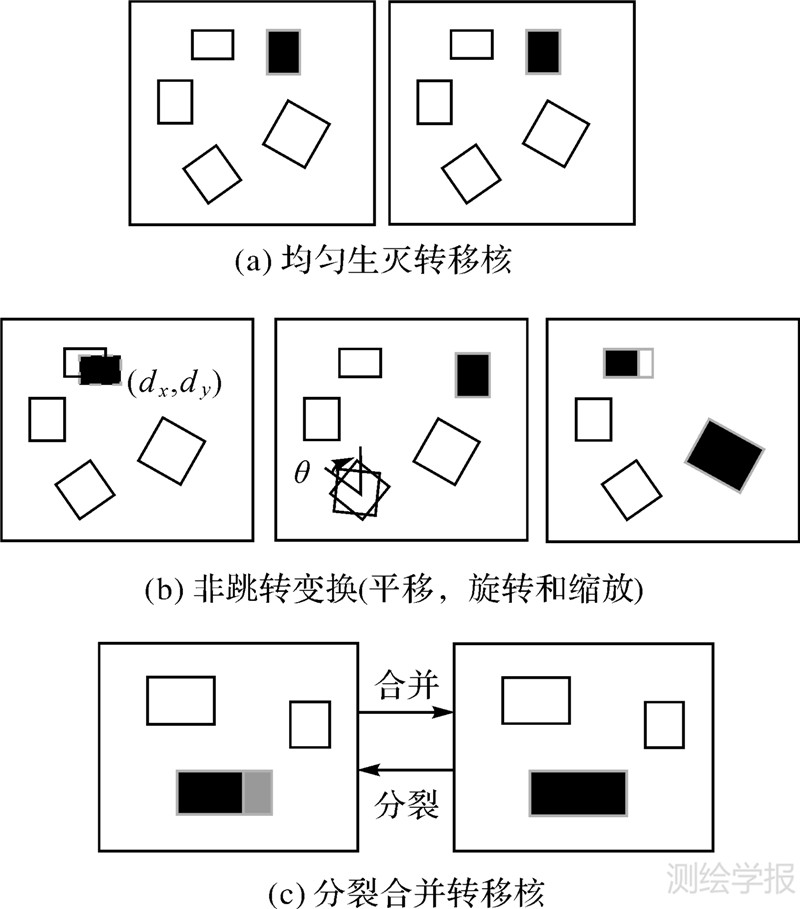
|
| 图 6 RJMCMC转移核 Fig. 6 Transition kernels of RIMCMC |
因为平移、旋转和缩放3种转移核不改变目标的数量,只是对当前目标的参数进行修改,故称之为非跳跃变换转移核。这3种转移核是为了使矩形更好的拟合目标。图 6(b)中黑色目标表示对选取目标进行平移、旋转和缩放的结果,每一次缩放只对目标的一条边进行修改。
分裂合并转移核避免对提取的目标探测不足或过探测。 在有些情况下,状态空间陷于局部吉布斯自由能变最小值,均匀生灭转移核和非跳跃变换转移核不能解决该问题,从而提出分裂合并转移核(见图 6(c)),该转移核可以有效地解决这一问题。
4.2 模拟退火算法
模拟退火算法是一种通用概率演算法,用来在一个大的搜寻空间内找寻命题的最优解[20]。该算法可以确保在任何初始状态空间下收敛于全局最优解。模拟退火算法具有渐近收敛性,已在理论上被证明是收敛于全局最优解的全局优化算法。模拟退火算法的应用很广泛,但其参数难以控制。实际应用中,由于必须考虑计算复杂度的切实可行性等问题,常采用如下的降温方式
本文采用ISPRS的机载激光扫描测试数据进行试验,其中包含树木、建筑物、道路等目标。分别对两组不同的数据进行试验。第1组数据的区域扫描范围约为247 m×179 m,共146 235个激光点。点云及生成的0.25 m分辨率的点云特征影像见图 7(a)、(b)。点云特征影像的大小为:988像素×715像素。第2组数据的区域扫描范围约为275 m×320 m,共351 692个激光点。点云及生成的0.25 m分辨率的点云特征影像见图 8(a)、(b)。点云特征影像的大小为:1098像素×1280像素。第1组数据的建筑物结构相对比较简单,第2组数据的建筑物结构比较复杂。

|
| 图 7 点云特征影像及多目标提取结果 Fig. 7 Point cloud feature image and multi-objects extraction result |

|
| 图 8 点云特征影像及多目标提取结果 Fig. 8 Point cloud feature image and multi-objects extraction result |
由于两组数据属于同一区域,本文对两组数据的试验参数进行相同的设置。根据建筑物及树冠的大小,设定矩形的长和宽的取值范围分别为[30, 200]和[30, 100],椭圆的长短半轴的取值范围为[16, 32],避免目标中心点重叠的距离阈值设置为椭圆短半轴的最小值;对于模拟退火的参数,一般初始温度为1000,最低温度为0.000 1,降温因子0.999 5,每一温度下运行次数100;泊松分布强度为提取目标的大体数量,与最终提取目标的数量无关,本文设置为70;通过对点云特征影像的梯度影像测试,梯度阈值为15时,目标的边缘较明确,且较完整。图 7(c)和图 8(c)分别展示了点云特征影像中建筑物和树冠的提取结果,其中椭圆形目标为树冠,矩形目标为建筑物(不考虑具有椭圆形等特殊形状的建筑物和特殊形状的树木)。图 7(d)、图 8(d)和图 7(e) 、图 8(e)则分别为提取建筑物和树冠的点云以及提取建筑物和树冠后的点云。试验结果见表 1。
由于第2组数据中建筑物的结构比较复杂,因此第2组数据中目标的马氏距离要比第1组数据中目标的马氏距离小一些,因此数据一致性因子阈值d0的取值也就小一些。通过图 7(c)、(d)、(e)和图 8(c)、(d)、(e)可以看出,该方法对于比较规则的、可分离的建筑物和树冠提取效果很好,且边界精确;对于比较复杂的建筑物和树冠也能粗略的提取出其轮廓,可根据该结果进行进一步的精细处理,确定目标的具体边缘。在第1组数据中可以提取出所有建筑物,并且提取的目标的边缘比较精确。对于第2组数据,结构比较简单的建筑物能得到较精确的提取结果,对比较复杂的建筑物也能粗略的提取出其轮廓。该方法也可以提取出大部分树冠,但是少部分树冠无法提出。总体来说,该试验结果达到了预期的目的。部分树冠无法提取出的原因如下:目标处于点云特征影像的边缘(无法计算数据一致性自由能变值)、目标较小或较大(超出提取目标给定的大小范围)、目标形状不规则、树冠与建筑物或树冠之间距离太近(不具有可分性)等因素。当树冠的形状接近于矩形时,可能被错误地提取为矩形目标,这主要是因为本文中的吉布斯自由能变模型只是考虑目标内部具有一致性,而没有加入目标的特征分析,仅依靠吉布斯自由能变模型不能对这类目标进行区分。对于建筑物和树冠的详细区分可以根据目标点云的空间密度分析等方法进行进一步区分。本文采用正确率和完整率对提取目标进行评价,对两组数据进行目标提取的正确率与完整率见表 2。
| 试验数据 | 正确 | 错误 | 遗漏 | 正确率 | 完整率 |
| 数据1 | 83 | 4 | 18 | 95% | 82% |
| 数据2 | 151 | 6 | 40 | 96% | 79% |
通过试验分析可知,数据一致性因子阈值d0用于归一化目标的数据一致性因子的取值。马氏距离的计算为目标内部区域和外部区域的均值差的平方与协方差的比,是一种相对关系,与点云特征影像的分辨率和提取目标的大小无关;与目标边缘的规则度以及与目标相邻的区域是否有其他目标存在相关。针对本文处理的数据,d0的取值范围为[1,1.5]。
本文算法只有一个参数需要调试,并把目标的梯度信息作为先验信息,可以克服文献[10, 11]方法的不足,能够有效地提取出建筑物和树冠。同时把吉布斯自由能变模型的数据一致性因子归一化到[-1, ]内,解决了文献[12]方法中吉布斯自由能变模型参数设置阈值范围过大、调试比较困难的问题。另外,本文算法不需要对点云特征影像进行预处理,消除了对影像进行预处理时造成目标及其边缘模糊的影响,提取结果更加精确。
与所有基于采样的方法一样,该方法的缺点是运行时间相对较长。该方法的效率和很多因素相关:数据大小、提取目标大小、目标间差异、目标数量、提取结果精度、背景复杂度、模拟退火中参数设置等。提高算法的效率,引入布朗运动等一些高效的优化算法是下一阶段的重点研究内容。
利用本文中的算法,可以同时得到建筑物和树木的数量、中心点位置、目标的大小以及目标的方向角等信息,可以用于估计城区的建筑物和植被绿化面积、确定和标注建筑物和树冠的位置和大小,对于城建部门掌握管理城市的建筑物及绿化状况、地图测绘人员丰富城市地图信息和三维建模等方面有着非常重要的使用价值。
6 结 论本文利用多标记点过程方法,从根据机载激光扫描数据生成的点云特征影像中自动提取建筑物和树冠。本文算法的优点为:① 本方法是一种基于对象的统计几何方法,可以较好地消除噪声对目标提取结果的影响;② 在点云特征影像中无需进行预处理,直接提取目标;③ 构建新的、能准确提取目标的吉布斯自由能变模型。试验证明该方法可以效地提取建筑物和树冠及其相应信息,并具有较强的稳健性。缺点为比较费时。下一步可以利用蛇形算法等方法跟踪出不规则建筑物和树冠的具体形状,使提取结果更加精确。同时,提高算法的效率也是本方法需要解决的问题之一。
| [1] | XIA Bing, SU Guozhong, ZHOU Mei, et al. Algorithms Study of High Precision Building Segmentation on LiDAR Data[J]. Microcomputer Information, 2010,26(11): 210-211. (夏冰, 苏国中, 周梅,等. LiDAR点云中高精度建筑物分割算法研究[J]. 微计算机信息, 2010,26(11): 210-211.) |
| [2] | LI Yunfan,MA Hongchao. New Method for Building Planar Objects Extraction from LiDAR Data[J]. Computer Engineering and Applications, 2011, 47(10): 5-7. (李云帆, 马洪超. 从LiDAR数据中提取建筑物平面目标的新方法[J]. 计算机工程与应用, 2011, 47(10): 5-7.) |
| [3] | KIM K, SHAN J. Building Roof Modeling from Airborne Laser Scanning Data Based on Level Set Approach[J]. 7ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(4): 1-14. |
| [4] | SOHN G, DOWMAN I. Data Fusion of Highresolution Satellite Imagery and LiDAR Data for Automatic Building Extraction[J] . ISPRS Journal of Photogrammetry and Remote Sensing, 2007( 62): 43-63. |
| [5] | CHENG Liang, GONG Jianya, LI Manchun, et al. 3D Building Model Reconstruction from Multi-view Aerial Images and LiDAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(6): 494-501. (程亮, 龚健雅, 李满春,等. 集成多视航空影像与 LiDAR数据重建 3维建筑物模型[J]. 测绘学报, 2009, 38(6): 494-501.) |
| [6] | VOSSELMAN G, DIJKMAN S. 3D Building Model Reconstruction from Point Clouds and Ground Plan[J].International Archives and Remote Sensin, 2001, 4(3W4): 37-43. |
| [7] | ZENG Qihong, MAO Jianhua, LI Xianhua, et al. Building Reconstruction from Airborne LiDAR Points Cloud Data[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 321-324. (曾齐红,毛建华, 李先华,等. 机载LiDAR点云数据的建筑物重建研究[J]. 武汉大学学报:信息科学版, 2011, 36(3): 321-324.) |
| [8] | LIU Linlin. The Application of Marked Point Process in Road Extraction[D]. Beijing: Institute of Electronics, Chinese Academy of Sciences, 2007. (刘琳琳. 标记点过程在道路提取中的应用[D]. 北京: 中国科学院电子学研究所, 2007.) |
| [9] | TOURNAIRE O, PAPARODITIS N. A Geometric Stochastic Approach Based on Marked Point Processes for Road Mark Detection from High Resolution Aerial Images[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2009, 64 (6): 621-631. |
| [10] | ORTNER M, DESCOMBES X, ZERUBIA J. Building Outline Extraction from Digital Elevation Models Using Marked Point Processes[J]. International Journal of Computer Vision, 2007, 72 (2): 107-132. |
| [11] | TOURNAIRE O, BREDIF M, BOLDO D, et al. An Efficient Stochastic Approach for Building Footprint Extraction from Digital Elevation Models[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(4): 317-327. |
| [12] | LAFARGE F, DESCOMBES X. ZERUBIA J, et al. Automatic Building Extraction from Dems Using an Object Approach and Application to the 3D-city Modeling[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63(3): 365-381. |
| [13] | PERRIN G, DESCOMBES X, ZERUBIA J. Point Processes in Forestry: An Application to Tree Crown Detection[R]. Sophia Antipolis: INRIA, 2005. |
| [14] | LAFARGE F, GIMELFARB G, DESCOMBES X. Geometric Feature Extraction by a Multi-marked Point Process[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1597-1609. |
| [15] | LI Bijun , FANG Zhixiang, REN Juan. Extraction of Building’s Feature from Laser Scanning Data[J]. Geomatics and Information Science of Wuhan University, 2003, 28(1): 65-70. (李必军, 方志祥, 任娟. 从激光扫描数据中进行建筑物特征提取研究[J] . 武汉大学学报:信息科学版, 2003, 28(1): 65-70.) |
| [16] | YANG Bisheng, WEI Zheng, LI Qingquan, et al. A Classification-oriented Method of Feature Image Generation for Vehicle-borne Laser Scanning Point Clouds[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 540-545. (杨必胜, 魏征, 李清泉, 等. 面向车载激光扫描点云快速分类的点云特征图像生成方法[J]. 测绘学报, 2010, 39(5): 540-545.) |
| [17] | SNYDER D L. Random Point Processes[M]. New York: John Wiley & Sons, 1975. |
| [18] | XUAN Guorong, CHAI Peiqi. Feature Selection Bhattacharyya Distance[J]. Pattern Recognition and Artificial I, 1996, 9(4): 324-329. (宣国荣, 柴佩琪. 基于巴氏距离的特征选择[J]. 模式识别与人工智能, 1996, 9(4): 324-329.) |
| [19] | GREEN P. Reversible Jump Markov Chains Monte Carlo Computation and Bayesian Model Determination[J]. Biometrika, 1995, 82(4): 711-732. |
| [20] | LAM J. An Efficient Simulated Annealing Schedule[D]. New Haven: Yale University, 1988. |