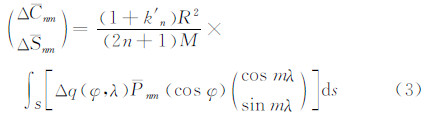2. 中国科学院 研究生院，北京 100049
2.Graduate University of Chinese Academy of Sciences, Beijing 100049, China
1 前 言
地球是一个复杂的动力学系统，其大气、海洋、冰雪融化、水循环、板块运动以及地震活动等因素导致地球系统内部质量变化，这些变化又会引起地球重力场变化，因此地球重力场是反映地球物质分布与运动的基本物理场。人卫激光测距技术(SLR)是目前研究低阶重力场系数变化最有效的技术手段，SLR得到的J2随时间的变化尺度从几小时到上百万年不等，存在着长期变化、季节性变化、年际变化和不规则变化等特性，国内外多位研究人员利用多颗或者单颗激光卫星的观测资料对J2的各种变化特性进行了分析研究[1, 2, 3, 4, 5, 6]。地球重力场变化是由地球内部质量变化引起的，因此利用大气表面气压、海底压和陆地水储量的全球网格数据，基于最新地球物理模型，可以从理论上模拟质量分布变化及其对地球重力场变化的影响，为研究地球重力场变化提供了另外一种独立的方法。文献[7,8,9]认为大气质量分布变化能较好地解释J2变化的周年项；文献[10]认为大气和陆地水是引起J2周年变化的主要原因，而J2的半年变化则主要是由海洋引起的；文献[11]通过研究认为大气是引起J2变化的主要原因。 GRACE (gravity recovery and climate experiment)计划是美国NASA和德国DLR联合研制项目，已于2002年发射，科学目标包括反演高精度高时空分辨率的静态及时变地球重力场等。到目前为止已经有9a多的观测数据，GRACE RL04已经提供一组地球重力场的系数值，时间间隔大约为30d[12]。文献[13,14],已将GRACE结果应用于研究地球内部质量变化。因此为了了解3种方法得到的地球重力场变化情况，本文将综合利用2002年4月至2010年10月Lageos1和Lageos2的SLR最新观测数据、最新的地球物理模型以及GRACE 3种独立方法来研究J2的季节性变化。
2 方 法 2.1 SLR数据分析本文利用上海天文台的SHORDE软件,采用数值积分方法，求出高精度的卫星星历和待求参数对卫星位置的偏导数，然后根据观测量的残差平方和最小准则估计参数。所有激光观测资料每15d为一个弧段，每个弧段估算的参数包括卫星位置和速度、地球重力场系数、太阳光压和大气类阻力，其中太阳光压每15d解算一组参数，大气类阻力每3d解算一组参数。
2.2 地球物理模型方法地球内部质量变化引起的地球外部某一点P处的引力变化，用n阶m次的Stokes球谐系数可以表示如下
式中，R为赤道半径；M为地球质量；ρ(r,φ,λ)为地球V内的密度；
为归一化量。
质量块ΔρdV的重新分配会引起地球惯性张量的变化，因此式(1)变为
如果Δρ(r,φ,λ)发生变化，则主要是发生在地球系统内部的大气、海洋和陆地水，表现为固体地球表面负荷的变化Δq(φ,λ)，因此有
考虑到地球是非刚体的，固体地球弹性形变可以通过Love数k′n来描述，因此式(2)可变为
式中，k′n为n阶Love数；k′2=－0.301[15]；Δq(φ,λ)为(φ,λ)处的表面负荷变化，对于大气、海洋和陆地水来说，Δq(φ,λ)分别为
(1) 大气：
式中，ΔP(φ,λ)为φ,λ表面气压变化；g为地球重力加速度。
此部分计算时，本文考虑大气压和海平面的相互作用，即分别按照反变气压计(IB)和不采用反变气压计(NIB)两种假设进行计算[16]。采用IB假设时，海洋上方气压变化则为海洋上所有观测时刻气压平均值。采用NIB假设时，海洋上方的气压变化则为测量值。
(2) 海洋(非潮汐)：
式中，ΔP(φ,λ)为(φ,λ)处的洋底压力的变化；g为地球重力加速度。
(3) 陆地水：
式中,ηi为土壤湿度; i为层数; h1=10cm; h2=190cm; ρ0=1g/cm3为水的密度；ΔN为雪、冰的等价水量。
2.3 GRACE方法GRACE RL04是基于新的重力场模型(GGM02C[17]和EGM96[18]两种重力场模型的组合)、新的周日和半周日海潮模型FES2004以及最新的SEPT模型。GRACE提供的重力场系数是经过潮汐改正之后的，包括固体潮、海潮以及固体地球极潮的改正。非潮汐的大气和海洋对重力场变化的贡献在Level-2产品中已经被扣除，因此在与SLR以及地球物理资料进行比较时，需要把已经扣除的非潮汐大气和海洋对重力场的贡献(GAC文件)加回到Level-2产品(GSM文件)中。
3 数 据 3.1 SLR数据本文采用的是2002年4月至2010年10月的Lageos1和Lageos2卫星的最新观测数据。
3.2 地球物理模型数据 3.2.1 海洋数据海洋数据采用的是estimating circulation and climate of the ocean(ECCO)模型，由jet propulsion laboratory(JPL)提供。该模型是基于Massachusetts Institute of Technology(MIT)的全球环流模型[19]和用于同化的Kalman滤波器。模型覆盖区域从-79.5°S~78.5°N，在赤道附近(-25.5°S~25.5°N)纬度方向分辨率为(1/3)°，在高纬度地区的纬度方向分辨率为1°，经度方向分辨率一直为1°。垂直方向分为46层，海面附近150m内垂直方向分辨率为10m。ECCO海洋模型数据包括10d平均的温度、盐度、海平面高(SSH)以及三维速度场和每12h的瞬时海平面高和海底压强数据。本文采用的是每12h的海底压强数据，数据可以从http://www.ecco-group.org网站下载，数据格式为NetCDF格式。
3.2.2 大气数据本文大气数据采用national centers environmental prediction(NCEP)再分析数据，空间分辨率为2.5°×2.5°经纬度网格，气压数据包括海平面气压和表面气压。 NCEP数据时间从1948年至今，数据的时间间隔有6h、1d和月均值3种，可以从http://www.ersl.noaa.gov/psd/data/reanalysis 网站下载得到。本文采用的是时间间隔6h的表面气压数据，数据格式为NetCDF格式。
3.2.3 陆地水数据采用由GSFC和NOAA共同研发的global land data assimilation system(GLDAS)数据[20]。GLDAS利用先进的模型和同化技术对最新的空间和地面观测系统提供数据进行计算。空间分辨率有1°和0.25°两种。本文采用的土壤湿度和冰雪数据可以从ftp://agdis.gsfc.nasa.gov 中下载，数据格式为GRIB格式。
3.3 GRACE数据从2002年至2010年底，GRACE RL04包括了大约100个月解，计算中需要的数据可以从ftp://podaac-ftp.jpl.nasa.gov/allData/grace/L2/CSR/RL04/中下载。
4 结果分析本文采用
，
。图 1(a)为大气质量变化引起J2变化的时间序列；图 1(b)为海洋和陆地水的质量变化引起J2变化的时间序列。从图 1(a)中可以看出，在IB假设下，大气质量变化引起的ΔJ2 值比其在NIB假设下引起的ΔJ2值小，前者ΔJ2时间序列变化范围大约在±2.0×10－10之间，而后者ΔJ2时间序列变化范围大约在±6.0×10－10之间，为前者的3倍左右。从图 1中还可以看出，大气、海洋和陆地水质量变化引起的ΔJ2各时间序列中存在着明显的季节性。图 2所示为SLR、GRACE以及地球物理模型(以AOW表示)计算得到的ΔJ2时间序列，从图中可以看出几种方法得到的ΔJ2彼此之间吻合得较好，同样都存在明显的季节特性。
|
| 图 1 大气、海洋和陆地水模型得到的ΔJ2时间序列 Fig. 1 Monthly ΔJ2 calculated from data of atmospheric surface pressure, ocean and surface water |
|
| 图 2 SLR、GRACE和AOW得到的ΔJ2时间序列 Fig. 2 The time series of ΔJ2 from SLR, GRACE and AOW |
文中对SLR和地球物理模型数据序列分别进行30 d的平滑，然后根据GRACE的时间通过内插进行统一。对GRACE、SLR以及AOW得到的ΔJ2时间序列进行周年和半年的拟合，振幅和相位结果如表 1所示，表中振幅A和相位φ的表示形式为Asin[ω(t－t0)+φ]，其中ω为频率，t0为参考历元，取值为2002-01-01。
对于ΔJ2的周年项而言，本文SLR得到的ΔJ2周年振幅为2.50×10-10，在NIB假设下大气引起的ΔJ2周年振幅为1.86×10-10，占SLR结果的70%左右，两者相位相差8°；在IB假设下大气引起的ΔJ2周年振幅为0.57×10-10，占SLR结果的23%，相位差59°。通过这两种假设得到的结果比较可得：采用NIB假设大气变化引起的ΔJ2周年振幅比其采用IB假设引起的ΔJ2周年振幅大3倍左右，相位相差47°。分析海洋数据可得海洋引起ΔJ2周年振幅占SLR观测结果的15%左右，相位相差9°，显然大气和海洋的质量变化还不能够完全解释SLR得到的J2季节变化，因此剩余的部分可能是由于陆地水引起的，通过分析陆地水的数据得到陆地水引起ΔJ2的周年振幅占SLR观测周年振幅的40%左右，两者相位相差28°。对于大气、海洋和陆地水质量变化引起ΔJ2的周年相位来说，在IB假设下大气引起ΔJ2的相位最小，海洋引起的相位最大，两者相位差异达到68°。通过以上的分析结果综合来看，大气、海洋和陆地水的质量变化基本上是可以解释SLR得到的ΔJ2季节变化，而且从大气、海洋和陆地水分别与SLR观测得到的ΔJ2相比较可得出：对ΔJ2周年影响主要是大气和陆地水的贡献，海洋贡献相对较小。
表 1还列出了其他文献通过地球物理模型和GRACE得到的周年项结果，可以看出本文地球物理模型得到的结果与文献[7, 10, 21]得到的周年振幅和相位结果比较吻合。本文GRACE得到的周年结果无论是振幅还是相位也都与文献[21]得到的结果接近，存在的差异是由于两者数据时间段不同，如果采用与文献[21]相同的时间数据，两者的结果有望吻合得更好。通过比较本文SLR、GRACE和AOW得到的ΔJ2周年项的结果可以看出，SLR得到的周年振幅与AOW结果吻合的相对更好，其振幅值介于AOW(IB)和AOW(NIB)的值之间，分别相差0.62×10-10和0.55×10-10。AOW与SLR振幅之间的差别可能主要是由于采用的地球物理模型存在误差，例如如果采用不同的陆地水模型得到的振幅可以差别1倍以上[22]。从表 1中的周年振幅值还可以看出，GRACE得到的周年振幅值最大，比SLR得到的振幅大50%左右。从图 2中ΔJ2时间序列也可以看出，GRACE得到的ΔJ2明显大于其他几种情况，尤其是在2006年之后，GRACE结果更大，这可能主要是由于本文采用的是Center for Space Reaseach(CSR)提供的GRACE数据，其与潮汐模型误差有较大的关系，尤其是海潮模型中的S2潮波(周期大约为161d)和K2潮波(周期大约为3.73a)误差，使得GRACE得到的ΔJ2变化存在着较大的年际变化[21]。对于ΔJ2周年相位而言，SLR、GRACE和AOW得到的相位相互之间符合较好，最大相差17°。
| 周年 | 半年 | |||
| 振幅(×10-10) | 相位/(°) | 振幅(×10-10) | 相位/(°) | |
| GRACE | 3.76 | 220 | 1.01 | 353 |
| GRACE[21] | 3.31 | 224 | 0.40 | 318 |
| SLR | 2.50 | 228 | 1.01 | 332 |
| Atmosphere(IB) | 0.57 | 169 | 0.09 | 64 |
| Atmosphere(NIB) | 1.86 | 216 | 0.27 | 19 |
| Ocean | 0.44 | 237 | 0.27 | 340 |
| Water | 1.10 | 200 | 0.25 | 345 |
| AOW(IB) | 1.88 | 211 | 0.49 | 7 |
| AOW(IB)[7] | 2.70 | 214 | 1.32 | 292 |
| AOW(IB)[10] | 2.26 | 233 | 0.16 | 230 |
| AOW(NIB) | 3.05 | 219 | 0.72 | 6 |
| AOW(NIB)[7] | 3.85 | 201 | 1.59 | 297 |
| AOW(NIB)[10] | 3.00 | 210 | 0.13 | 215 |
| AOW[21] | 3.06 | 230 | 0.22 | 343 |
对于本文得到的ΔJ2半年项，在NIB假设下的大气、海洋和陆地水3项引起ΔJ2的半年振幅值相当，占SLR得到的半年的振幅25%左右，而在IB假设下大气引起的ΔJ2振幅值则比在NIB假设下大气、海洋和陆地水的结果都小，占三者振幅值的30%左右，占SLR结果的10%左右。海洋、陆地水分别与SLR得到的半年相位吻合较好，最大相差13°，而大气变化引起的ΔJ2半年相位值相对较大，尤其是在IB假设下得到的结果，与SLR得到的半年相位值相差达到92°。海洋和陆地水的变化引起的ΔJ2半年相位值吻合较好，仅相差5°，在NIB和IB假设下大气变化引起的ΔJ2半年相位值与海洋、陆地水的质量变化引起ΔJ2相位值分别相差36°和82°左右。
本文AOW得到ΔJ2的半年的振幅与文献[7, 10, 21]结果相互之间差别相对稍大，本文得到的半年振幅小于文献[7]结果，大于其他两篇文献结果，而本文得到的半年的相位则大于3篇文献结果。本文GRACE得到的半年振幅和相位与文献[21]结果的差别也是由于本文与文献[21]采用的数据时间段不同，如果本文采用同样时间内的数据得到的结果值就与文献[21]得到半年振幅和相位值更相符。通过比较本文GRACE、SLR和AOW得到的ΔJ2半年的振幅和相位结果可得：GRACE与SLR得到的ΔJ2半年的振幅相同，而且都大于AOW结果；AOW(IB)得到的ΔJ2半年振幅占SLR结果的48%左右，AOW(NIB)得到的ΔJ2振幅值占SLR结果的70%左右，因此与AOW(IB)得到的ΔJ2半年振幅相比，AOW(NIB)得到的ΔJ2半年振幅更接近于SLR得到的半年振幅。对于相位来说，GRACE、SLR和AOW 3种方法得到的ΔJ2半年的相位最大相差35°。从本文通过各种方法得到的结果以及本文与其他文献得到的结果来看，ΔJ2半年的振幅和相位不稳定，这主要是由于半年周期信号受到噪声影响较大，因而就会产生大的误差[23]。
表 2所示为SLR、GRACE以及AOW 3种方法得到的ΔJ2时间序列之间的相关系数，其中GRACE/SLR代表GRACE与SLR，AOW(IB)/SLR代表在IB假设下AOW与SLR，其他亦相同表示方法。从表中可以看出：在NIB假设下，AOW与SLR结果之间具有最大的相关性，相关系数为0.67；而GRACE与SLR结果之间的相关性则最小，相关系数为0.54。通过以上各结果周年、半年振幅和相位的比较以及相互之间的相关性来看，可以说SLR是目前检验地球物理模型和GRACE结果的一种有效方法。
| 相关系数 | ||
| AOW(IB)/GRACE | 0.63 | |
| AOW(NIB)/GRACE | 0.65 | |
| AOW(IB)/SLR | 0.64 | |
| AOW(NIB)/SLR | 0.67 | |
| GRACE/SLR | 0.54 | |
本文利用2002年4月至2010年10月的Lageos1和Lageos2激光卫星观测、GRACE以及地球物理模型3种独立的方法计算地球低阶重力场J2的变化，重点分析了ΔJ2的季节特性，通过结果分析表明：
(1) AOW、SLR和GRACE 3种方法所得到的ΔJ2变化都存在明显的季节特性。
(2) 在NIB假设下大气质量变化引起的ΔJ2周年振幅比其在IB假设下引起的ΔJ2周年振幅大3倍左右，相位相差47°，SLR得到的ΔJ2周年振幅介于两种假设下大气得到的结果之间；大气和陆地水对ΔJ2周年变化的贡献占主导地位，海洋的影响较小。
(3) 大气、海洋和陆地水质量变化引起的ΔJ2半年振幅与SLR得到的半年振幅和相位差异较大，尤其在IB假设下大气变化引起的ΔJ2相位值与SLR得到的结果相差92°，振幅占SLR结果的10%左右。
(4) SLR、GRACE以及地球物理模型3种方法得到的ΔJ2周年振幅和相位相互之间吻合的较好，3种方法得到的相位值相差最大仅17°； SLR得到的周年振幅与AOW得到的结果相对更吻合，而且介于AOW(IB)和AOW(NIB)2种情况得到的振幅值之间；GRACE得到的周年振幅值最大，比SLR得到的振幅大50%左右； GRACE与SLR得到的半年振幅相同，AOW(IB)得到的半年振幅和相位与SLR结果相差最大。
致谢：本项研究在武汉大学地球空间环境与大地测量教育部重点实验室完成。| [1] | YODER C F,WILLIAMS J G,DICKEY J O,et al.Secular Variation of Earth's Gravitational Harmonic J2 Coefficient from Lageos and Nontidal Acceleration of Earth Rotation[J].Nature,1983,303(10):757-762. |
| [2] | COX C M,CHAO B F.Detection of a Large-scale Mass Redistribution in the Terrestrial System Since 1998[J].Science,2002,297(5582):831-833. |
| [3] | CHENG M K,SHUM C K,TAPLEY B D.Determination of Long-term Changes in the Earth's Gravity Field from Satellite Laser Ranging Observations[J].Journal of Geophysical Research,1997,102(B10):6216-6236. |
| [4] | CHENG M K,TAPLEY B D.Variations in the Earth's Oblateness during the Past 28 Years[J].Journal of Geophysical Research,2004,109(B9):3028-3036. |
| [5] | PENG Bibo,WU Bin,XU Houze.Determination of Long Term Variations of Low Degree Geopotential Field[J].Acta Geodaetica et Cartographica Sinca,2000,29(S1):38-42.(彭碧波,吴斌,许厚泽.低阶地球引力场长期变化的确定[J].测绘学报,2000,29(S1):38-42.) |
| [6] | QU Weijing,WU Bin.Analysis of the Characteristics of the Harmonics Coefficient J2 of the Earth's Gravity Field in Different Periods[J].Chinese Science Bulletin,2012,57(14):1626-1630. |
| [7] | CHAO B F,EANES R J.Global Gravitational Changes due to Atmospheric Mass Redistribution as Observed by the Lageos Nodal Residual[J].Geophysical Journal International,1995,122(3):755-764. |
| [8] | CHAO B F,AU A Y.Temporal Variations of the Earth's Low-degree Zonal Gravitational Field Caused by Atmospheric Mass Redistribution:1980-1988[J].Journal Geophysical Research,1991,96(B4):6569-6575. |
| [9] | GEGOUT P,CAZENAVE A.Temporal Variations of the Earth Gravity Field for 1985-1989 Derived from Lageos[J].Geophysical Journal International,1993,114(2):347-359. |
| [10] | DONG D,GRINS R S,DICKEY J O.Seasonal Variations of the Earth's Gravitational Field:An Analysis of Atmospheric and Ocean Tidal Excitation[J].Geophysical Research Letter,1996,23(7):725-728. |
| [11] | WU Bin.Variations of Earth Rotation and Geopotential[J].Acta Geodaetica et Cartographica Sinca,2001,30(1):6-9.(吴斌.地球引力场与地球自转变化[J].测绘学报,2001,30(1):6-9.) |
| [12] | TAPLY B D,BETTADPUR S,WATKINS M M,et al.The Gravity Recovery and Climate Experiment:Mission Overview and Early Results[J].Geophysical Research Letter,2004,31(9):1029-1034. |
| [13] | CHEN J L,WILSON C R,TAPLAY B D,et al.Low Degree Gravity Changes from GRACE:Validation and Interpretation[J].Geophysical Research Letter,2004,21(11):1-5. |
| [14] | CHEN J L,WILSON C R.Low Degree Gravity Changes from GRACE,Earth Rotation,Geophysical Models,and Satellite Laser Ranging[J].Journal Geophysical Research,2008,113(B6):1-9. |
| [15] | FARRELL W E.Deformation of the Earth by Surface Loads[J].Reviews of Geophysical,1972,10(3):761-797. |
| [16] | YAN Haoming.Inverted Barometer Response and It's Affect on the Earth's Rotation[D].Wuhan:Institute of Geodesy and Geophysics of CAS,1999.(闫昊明.反变气压计响应及其对地球自转的影响[D].武汉:中国科学院测量与地球物理研究所,1999.) |
| [17] | TAPLEY B D,RIES J,BETTADPUR S,et al.GGM02:An Improved Earth Gravity Field Model from GRACE[J].Journal of Geodesy,2005,79(8):467-478. |
| [18] | LEMOINE F G,KENYON S C,FACTOR J K,et al.The Development of the Joint NASA GSFC and the NIMA Geopotential Model EGM96:NASA/TP-1998-206861[R].Greenbelt:Goddard Space Flight Center,1998. |
| [19] | FUKUMORI I,LEE T,MENEMENLIS D,et al.A Dual Assimilation System for Satellite Altimetry[R].Miami Beach:Joint TOPEX/POSIDON and Jason-1 Science Working Team Meeting,2000. |
| [20] | RODELL M.The Global Land Data Assimilation System[J].Bulletin of American Meteorologycal Society,2004,85(3):381-394. |
| [21] | CHEN J L,WILSON C R.Assessment of Degree-2 zonal Gravitational Changes from GRACE,Earth Rotation,Climate Models,and Satellite Laser Ranging[C]//Gravity,Geoid and Earth Observation:International Association of Geodesy Symposia:135.Chania:Springer,2010:669-676. |
| [22] | YAN Haoming.Oceanic Roles in the Variations of Earth's Rotation and Gravity Field[D].Wuhan:Institute of Geodesy and Geophysics of CAS,2005.(闫昊明.海洋在地球自转和重力场变化中的作用[D].武汉:中国科学院测量与地球物理研究所,2005.) |
| [23] | TAPLEY B D,CHAMBERS D P,SHUM C K,et al.Accuracy Assessment of the Large-scale Dynamic Ocean Topography from TOPEX/Poseidon Altimetry[J].Journal Geophysical Research,1994,99(C12),24605-24618. |