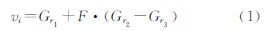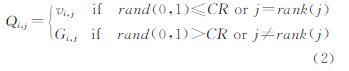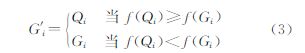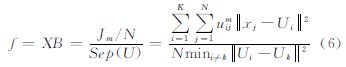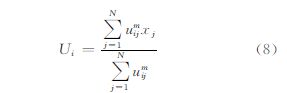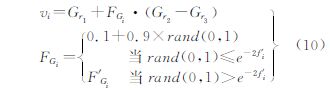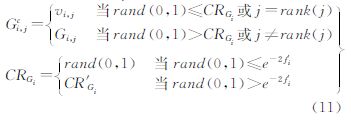1 引 言
遥感影像因其分辨率的限制存在着大量混合像元,混合像元现象制约了遥感影像的提取精度和应用范围[1, 2, 3]。传统的遥感影像聚类方法,如k均值[4]和ISODATA[5]等,大多属于硬聚类方法,该类方法直接将像元归属到某个类别,由于未考虑到同一像元中可能包含不同类别地物的情况,难以解决地物混合问题[6]。传统的模糊聚类方法(如模糊k均值)因采用隶属度表示像元属于各个类别的程度,能够获得比传统的硬聚类方法更好的分类结果,被广泛应用于遥感影像分类中[1, 2, 7, 8],但其仍然存在以下3个难点问题有待解决:① 无法自动地确定类别数[9, 10];② 容易陷入局部最优解[6],其聚类精度仍有待提高;③ 分类结果受初始聚类中心位置的影响较大[11]。
针对以上难点,近年来国内外学者开始尝试利用进化算法进行影像自动聚类的研究[10],提出了不同的影像自动聚类方法。文献[12]提出了一种利用PSO算法,通过硬聚类有效性指标来确定影像类别数的影像自动分类方法;文献[9]提出了基于差分进化算法(DE)来寻找影像的类别数的硬聚类算法。之后,文献[6]和文献[10]分别将模糊聚类有效性指标引入自动聚类,实现了对遥感影像的自动模糊聚类。但是这些方法由于搜索空间巨大,往往仅适用于较小的模拟数据,在处理波段较多的遥感影像时需要对影像进行降维处理才能得到较好的效果。
为了提高自动模糊聚类方法的性能,解决当搜索空间过大时进化自动聚类算法无法有效寻找到聚类中心的合理位置等问题,本文提出一种基于自适应差分进化的遥感影像自动模糊聚类方法(automatic fuzzy clustering based on self-adaptive differential evolution for remote sensing imagery,AFCDE)。该方法能够在无需先验类别数目信息的情况下,自动获取最优遥感影像聚类结果。差分进化算法由文献[13]于1995年提出,因其具有编码简单、搜索速度快等优点,已广泛应用于信号处理、数值优化、模式识别等多个领域[14]。然而传统差分进化算法也存在依赖先验知识,需要人工选择控制参数的问题。为了充分利用差分进化最优化能力和避免其参数选择问题,本文算法以Xie-Beni指数[15, 16]作为适应度指标,利用自适应变异方法对DE算法的主要参数步长因子F以及交叉率CR进行自适应选择,构建自适应DE方法,在对聚类中心进行实数和二进制掩码(1表示该聚类中心被选择,0表示不选择)编码后,通过自适应DE算法进行聚类数目自动搜索,并针对遥感影像自动聚类空间较大的特点,结合局部搜索操作以减小算法搜索范围,获取合理类别数及最优聚类结果。
2 差分进化算法差分进化算法(differential evolution,DE)是近年来快速发展的一种简单而有效的进化算法,已被成功应用于求解无约束单目标和多目标优化问题[12, 13]。该算法在保留基于种群的全局搜索方式的基础上,采用实值编码,通过差分变异与交叉产生后代。子代个体与父代个体之间进行一对一的淘汰选择,保留适应度高的个体,从而在迭代过程中实现进化,最终达到搜索全局最优解的目的。具体过程如下:
首先,对种群进行随机初始化。之后,进行变异操作,变异公式如式(1)所示,其中,vi为新产生的个体;F是步长因子,0<F≤1;Gr1、Gr2、Gr3代表从种群中随机选取的3个个体;r1、r2、r3为1到NP之间的随机整数,且r1≠r2≠r3
将vi与其对应的父代个体Gi按式(2)进行交叉,得到候选个体Qi={Qi,1,Qi,2,…,Qi,j…Qi,d} 式中,CR∈[0,1]为交叉率因子。rand(0,1)是一个[0,1]范围内的随机数,j表示个体Gi第j维的数值,rank(j)为0到d的随机整数。通过式(3)进行新旧个体间的选择,淘汰掉适应度低的个体 式中,G′i表示下代种群中的第i个个体。在得到新一代的种群之后,重复以上计算步骤,直到满足算法终止条件,最后记录下全局最优个体Gbest。DE算法具有计算简单等优点,已在影像处理[17]、电力系统设计[18]、生物信息[19]、传感网优化[20]、信号处理[21]等领域得到了广泛应用,但主要控制参数 F和CR通常需要人工指定,依赖于先验知识,这也限制了其适用范围,特别是对于数据量较大的遥感影像聚类,其参数的选择往往需要耗费很多的时间。
3 AFCDE方法为了提高DE的自适应性,并利用差分进化稳健的全局搜索能力进行遥感影像聚类,本文提出了AFCDE。该方法对聚类中心进行实数编码,在聚类过程中以模糊聚类类别判决函数Xie-Beni指数作为适应度函数,通过差分进化的变异、交叉、选择等算子自动确定类别数目,同时为了减少算法对于DE参数的影响,采用自适应方法更新DE参数值以获得最优聚类结果。其具体过程如下。
3.1 种群初始化为了实现遥感影像自动聚类,首先对初始种群中的NP个个体进行聚类编码。对于每个个体,其编码为Gi=[Gi,1,G,i2,…,Gi,j,…,Gi,l],其中,l=C×d;C为聚类中心的最大个数;d代表着每个聚类中心的维数。对于遥感影像,d表示遥感影像的波段数。为了自动选择聚类中心的个数,每个个体都对应一个长度为C的二值掩膜,MaskerGi=[B1,B2,…Bt…,BC],表示C个聚类中心中哪些被选择,当Bt的取值为1时,代表第t个聚类中心被选择;而当Bt为0时,表示第t个聚类中心未被选择。种群个体Gi的初始化采用随机赋值的方式,如式(4)所示
式中,Gmax,j和Gmin,j分别表示个体Gi在第j位上的最大值和最小值。个体Gi对应的二值掩膜通过0到1的随机概率函数rand()来初始化,如式(5)图 1以波段数为2,最大聚类数为4的遥感影像进行聚类为例,显示其编码及掩码的结果,其中,个体的长度l=2×4,类别1和3的二值掩码为1,表示该聚类中心被选择。

|
| 图 1 AFCDE算法个体编码 Fig. 1 Individual encoding of AFCDE algorithm |
为了进行适应度的计算,需要将个体Gi中掩码值为1的部分解码成遥感影像的聚类中心Ui,i为聚类中心的序号,0<i≤K,0<K≤C,C为个体Gi包含的最大类别数,K为通过3.1节二值掩码被选中的聚类中心的总数。以图 1中所示个体Gi为例,解码后成为U1和U2两个聚类中心,如图 2所示。

|
| 图 2 AFCDE算法个体解码 Fig. 2 Individual decoding of AFCDE algorithm |
为了获得最优聚类数,本文利用文献[15]中 (XB)系列指数作为DE的适应度函数f。Xie-Beni系列指数是一种遥感影像模糊聚类有效性评价指标[22],能够有效地获得遥感影像最优分类数,计算如式(6)
式中,K代表类别数;N为遥感影像像元的总数;xj为遥感影像中的第j个像元;Ui和Uk分别表示第i和第k类的聚类中心;uij代表隶属度;m为模糊度指数;‖·‖表示欧几里得距离;f为适应度函数。uij和Ui的计算公式见式(7)和式(8) 从式(6)可知,分子Jm/N衡量的是各个像素到聚类中心距离的加权平均值。Jm/N较小时,表示聚类效果良好,类别内部紧凑;分母Sep(U)表示的是聚类中心之间距离的最小值,Sep(U)较大表示不同的类别之间有着更好的分离度。因此,较好的聚类效果应该具有较小的XB值。在AFCDE中计算适应度时,只有被选择的聚类中心才会用于计算XB值。在每次计算适应度前,使用式(7)和式(8)对聚类中心进行更新,加快算法的运算速度[6, 23]。
3.4 个体的自适应变异交叉为了提高AFCDE的自适应性,本文方法采用自适应变异方法对步长因子F以及交叉率CR进行自适应选择[24],提高算法搜索的性能。
首先,在每一代计算的开始,求出每个个体的归一化适应度f′i
式中,fi表示的是第i个个体的适应度,通过式(6)计算; fmax为每代种群适应度的最大值。适应度函数值越低,表示该值越好,变异的可能性则越大。为实现该过程,在AFCDE中每个个体Gi均有自己的步长因子FGi和交叉率CRGi,且以一定的概率遗传至下一代。具体如下:通过式(10)求得每个个体的FGi,并进行差分变异操作,产生新的个体vi,再利用式(11)计算个体的CRGi,将vi与对应父代个体进行交叉,得到候选个体Gic ={Gi,1c,Gi,2c,…,Gi,jc,…,Gi,lc}
式中,r1、r2、r3为1到NP之间的随机整数,且r1≠r2≠r3。F′Gi和CR′Gi为个体Gi上一代的步长因子和交叉率。通过自适应地选择F和CR,表现好的个体拥有更多的更新参数的机会,使得计算资源在种群中进行合理的分配,从而提高整个算法的搜索性能。
3.5 选 择根据式(12),将候选个体与相应的父代中的个体进行一对一地比较,淘汰掉适应度低的个体,保留适应度高的个体
3.6 最优类别数的搜索在进行完以上步骤之后,需要对个体以及个体的掩膜进行更新。若满足条件rand(0,1)<(f′)2,则使用式(6)对个体的掩膜进行重置。
3.7 局部搜索由于遥感影像的波段数较多,搜索空间较大,其进化结果往往难以收敛。为了提高AFCDE的搜索效率和结果,本文采用局部搜索算子提高算法的效率,即当最优个体Gbest在进化过程中连续g代不发生变化时,认为程序已搜索到最佳的类别数,将Gbest的掩膜所激活的类别个数认为是最优类别数,把Gbest的掩膜赋给种群中的其余个体MaskerGi=MaskerGbest,停止掩膜更新,再进行类别数固定下的最优聚类中心搜索,以减小算法的搜索空间,提高优化效率。
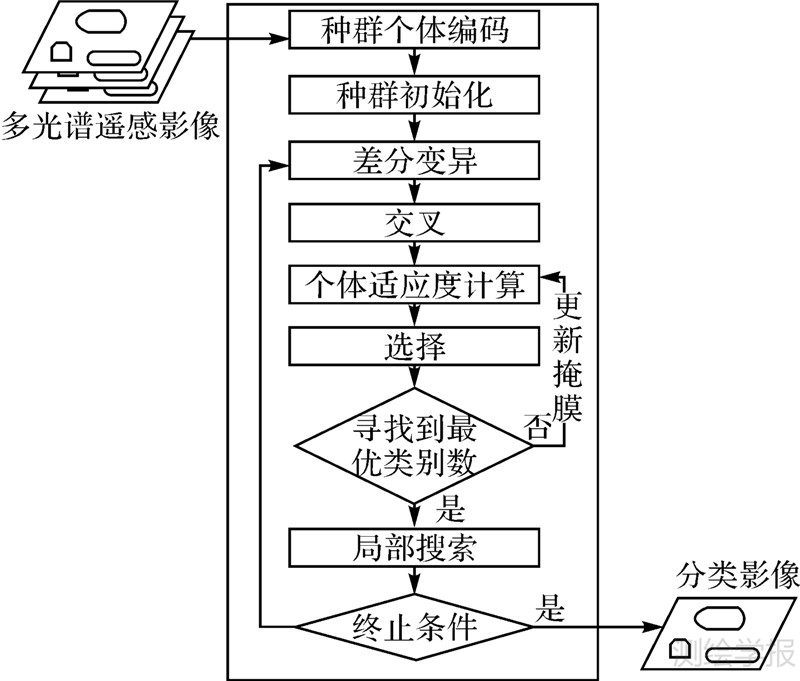
3.8 终止条件两代最优个体Gbest之间适应度的差值在给定的阈值范围之内或迭代次数达到最大迭代次数Tmax时算法终止。算法的流程图如图 3所示。
|
| 图 3 AFCDE算法流程图 Fig. 3 Flow chart of AFCDE |
为了验证AFCDE算法的有效性,本文选了两幅真实遥感影像进行分类试验,并与k均值、模糊k均值、ISODATA算法以及自动聚类算法FCIDE[10] (fuzzy clustering with an improved differential evolution)进行了结果对比。分类过程中对于XB指数中的模糊度指数m,在试验1中设置为3,试验2中设置为2。
4.1 Flightline C1数据本试验影像为机载扫描仪获取的Flightline C1 (FLC1)数据中的一部分,如图 4(a)所示,该数据共12波段,大小为92像素×107像素。影像为美国印第安纳州Tippecanoe县南部的一个农业区。其真实地物类型分布情况如图 4(b)所示。测试样本数据均通过实测获得,共包含玉米、燕麦、红苜蓿和小麦4个类别,各类地物的样本数目分别为1743、715、1700、1472,共计5630。

|
| 图 4 FLC影像分类结果图 Fig. 4 Classification result of FLC image |
图 4(c)~(g)分别表示k均值、ISODATA、模糊k均值、FCIDE和AFCDE的分类结果。ISODATA和k均值算法在分类时对聚类的数目进行了人工的指定。从目视效果上可以看出,k均值和ISODATA的分类结果较为相似。两者无法正确地将燕麦类进行区分,并且将苜蓿类以及玉米类中的一部分像素错分成其他类别的作物;模糊k均值算法、FCIDE和AFCDE算法在目视效果上比较接近,明显优于k均值和ISODATA算法,三者对于燕麦和小麦类的划分情况基本相同,但在光谱特征较为接近的红苜蓿以及玉米类的划分中,AFCDE的错分现象要少于模糊k均值算法。
表 1和表 2描述了各分类器的混淆矩阵和精度的定量比较结果。AFCDE算法在无需指定类别数的情况下,其总体精度比需要事先指定类别信息的k均值、ISODATA、模糊k均值算法分别提高了14.62%、14.62%和0.25%。与同样具有搜索类别能力的FCIDE算法相比,AFCDE由于在确定类别数目之后利用局部搜索算子有效地缩小了算法的搜索空间,精度提高了1.34%。AFCDE算法能够比其他算法表现得更优异的原因,在于其利用了自适应差分进化全局搜索能力,并通过自适应调整参数提高算法的性能,摆脱了由于聚类中心初始化以及在迭代过程中陷入局部最优解对结果所造成的影响,从而在处理较为复杂地物的分类问题上取得了最优的结果。
| 算法 | 类别 | 玉米 | 燕麦 | 红苜蓿 | 小麦 | 总计 |
| k均值 | 玉米 | 1715 | 159 | 606 | 0 | 2480 |
| 燕麦 | 15 | 0 | 76 | 0 | 91 | |
| 红苜蓿 | 5 | 0 | 1018 | 0 | 1203 | |
| 小麦 | 8 | 556 | 0 | 1472 | 2036 | |
| ISODATA | 玉米 | 1715 | 159 | 606 | 0 | 2480 |
| 燕麦 | 15 | 0 | 76 | 0 | 91 | |
| 红苜蓿 | 5 | 0 | 1018 | 0 | 1203 | |
| 小麦 | 8 | 556 | 0 | 1472 | 2036 | |
| 模糊k均值 | 玉米 | 1702 | 8 | 560 | 0 | 2270 |
| 燕麦 | 30 | 707 | 0 | 7 | 744 | |
| 红苜蓿 | 11 | 0 | 1140 | 9 | 1151 | |
| 小麦 | 0 | 0 | 0 | 1465 | 1465 | |
| FCIDE | 玉米 | 1620 | 7 | 472 | 0 | 2099 |
| 燕麦 | 73 | 633 | 0 | 7 | 706 | |
| 红苜蓿 | 50 | 1 | 1228 | 0 | 1279 | |
| 小麦 | 0 | 74 | 0 | 1472 | 1546 | |
| AFCDE | 玉米 | 1632 | 12 | 451 | 0 | 2095 |
| 燕麦 | 34 | 677 | 0 | 2 | 713 | |
| 红苜蓿 | 77 | 1 | 1249 | 0 | 1327 | |
| 小麦 | 0 | 25 | 0 | 1470 | 1495 | |
| 总计 | 1743 | 715 | 1700 | 1472 | 5630 |
| 精度 | k均值 | ISODATA | 模糊 k均值 | FCIDE | AFCDE |
| 总精度/(%) | 74.689 2 | 74.689 2 | 89.058 | 87.97 | 89.31 |
| Kappa系数 | 0.644 6 | 0.644 6 | 0.849 8 | 0.834 9 | 0.853 |
在对FLC数据进行分类的试验中,AFCDE所获得的XB指数值最低,为0.108,优于FCIDE的0.123 5及模糊k均值的0.271。另外,在独立运行的30次试验中,AFCDE找到正确类别数的次数为21,而FCIDE则仅有7次,其原因在于FCIDE方法在原始搜索空间中进行全局搜索,由于遥感影像波段较多,其搜索空间范围太大,降低了搜索到最优类别数的概率。而AFCDE方法采用了局部搜索算子,在保持算法精度的同时,减少了算法的搜索空间,并提高了算法的搜索效率。
4.2 武汉地区TM影像本试验采用了一幅武汉地区的TM影像。如图 5(a)所示,该影像共有6个波段,大小为1000像素×1000像素,空间分辨率为30 m,影像的采集时间为2002年7月。其测试样本数据如图 5(b)所示,主要通过实地调查,并结合人工解译的方法获得。该测试数据包含了46 475个样本,主要包含5类地物,分别是树木、道路、农田、水体以及城区,各类地物的测试样本数目分别为 8396、2105、6318、16 675、12 981,各种地物的测试数据均分布广泛,具有较好的代表性。

|
| 图 5 武汉TM影像分类结果及测试数据 Fig. 5 Classification image of Wuhan TM and test samples |
图 5(c)~(g)分别为k均值、ISODATA、模糊k均值、FCIDE、AFCDE的分类影像图。此幅影像地物复杂性较高,地物混合分布情况较为严重,而k均值算法和ISODATA算法处理存在大量混合地物的分类能力较弱,因此在指定了正确类别数的情况下仍然出现了较为严重的错分现象,未能区分出道路类别,且水体和城区之间存在着大量的错分现象。FCIDE算法对水体和城区之间做出了正确的划分,但将城区中的部分道路地物错分为了植被。模糊k均值算法在视觉效果上明显优于之前的3种算法,有效地将水体与城区以及道路与植被之间区分开来。AFCDE算法与模糊k均值算法相比,不仅对水体与城区、道路与植被进行了有效的区分,同时显著提高了城区和道路之间分类的准确性。
为了进一步验证AFCDE算法的准确性,将分类结果之间进行了定量的精度比较,比较采用的指标分别为混淆矩阵、总精度和Kappa表 3对各算法的混淆矩阵进行了对比,表 4利用测试样本对5种算法的总精度与Kappa系数进行了比较。在处理武汉地区遥感影像的分类问题时,AFCDE算法在自动获取类别数的同时取得了85.63%的精度,比k均值、ISODATA、模糊k均值以及FCIDE分别提高了23.84%、23.84%、3.38%、3.86%的精度。
| 算法 | 树木 | 道路 | 农田 | 水体 | 城区 | 总计 | |
| k均值 | 树木 | 4 686 | 37 | 75 | 0 | 1 493 | 6 291 |
| 道路 | 40 | 2 004 | 5 | 0 | 5 977 | 8 026 | |
| 农田 | 3 556 | 1 | 6 222 | 2 | 535 | 10 316 | |
| 水体 | 61 | 1 | 16 | 10 860 | 31 | 10 969 | |
| 城区 | 53 | 62 | 0 | 5 813 | 4 945 | 10 873 | |
|
ISO- DATA | 树木 | 4 698 | 37 | 75 | 0 | 1 496 | 6 291 |
| 道路 | 40 | 2 204 | 5 | 0 | 5 977 | 8 026 | |
| 农田 | 3 556 | 1 | 6 222 | 2 | 535 | 10 316 | |
| 水体 | 61 | 1 | 16 | 10 860 | 31 | 10 969 | |
| 城区 | 53 | 62 | 0 | 5 813 | 4 945 | 10 873 | |
|
模糊 k均值 | 树木 | 6 954 | 3 | 1 158 | 0 | 100 | 8 215 |
| 道路 | 61 | 1 952 | 5 | 0 | 3 732 | 5 750 | |
| 农田 | 1 022 | 14 | 5 125 | 124 | 1 353 | 7 638 | |
| 水体 | 42 | 2 | 0 | 16 541 | 46 | 16 631 | |
| 城区 | 317 | 134 | 30 | 10 | 7 750 | 8 241 | |
| FCIDE | 树木 | 6 263 | 0 | 928 | 0 | 54 | 7 245 |
| 道路 | 802 | 1 861 | 16 | 0 | 2 794 | 5 473 | |
| 农田 | 1 282 | 4 | 5 366 | 7 | 773 | 7 432 | |
| 水体 | 46 | 2 | 0 | 15 239 | 86 | 15 373 | |
| 城区 | 3 | 238 | 8 | 1 429 | 9 274 | 10 952 | |
| AFCDE | 树木 | 7 139 | 5 | 1 245 | 0 | 168 | 8 557 |
| 道路 | 41 | 1 825 | 2 | 0 | 2 139 | 4 007 | |
| 农田 | 987 | 12 | 5 052 | 50 | 1 439 | 7 540 | |
| 水体 | 44 | 2 | 0 | 16 596 | 49 | 16 691 | |
| 城区 | 185 | 261 | 19 | 29 | 9 186 | 9 680 | |
| 总计 | 8 396 | 2105 | 6 318 | 16 675 | 12 981 | 46 475 |
| 精度 | k均值 | ISODATA | 模糊 k均值 | FCIDE | AFCDE |
| 总精度/(%) | 61.79 | 61.79 | 82.25 | 81.77 | 85.63 |
| Kappa系数 | 0.514 8 | 0.514 8 | 0.769 8 | 0.760 2 | 0.809 4 |
在30次的运行中,AFCDE有26次得到了正确的类别数,高于FCIDE的24次。另外,在分类试验中,AFCDE获得了最低的XB指数,为0.144,优于FCIDE的0.149及模糊k均值的0.231。
4.3 算法复杂度分析AFCDE算法的计算复杂度,主要由以下几部分构成:
(1)初始化。AFCDE算法需要的时间为O(NP·l),其中,NP代表的是种群中的个体数;l代表的是个体向量的长度,l= K·D。其中,K为最大聚类数目;D为遥感影像的波段数。
(2)适应度的计算。① 计算N个点对应于K个聚类中心的时间复杂度为O(N·l),N代表的是遥感影像中像元的个数;② 更新K个聚类中心的复杂度为O(l);③ 对应种群中单个个体适应计算的时间复杂度为O(N·l)。因此,计算适应度的总时间复杂度为O(NP·N·l)。
(3)交叉变异操作。每代交叉变异的时间复杂度为O(NP·l)。
(4)个体淘汰。进行新旧个体之间淘汰选择的复杂度为O(NP)。
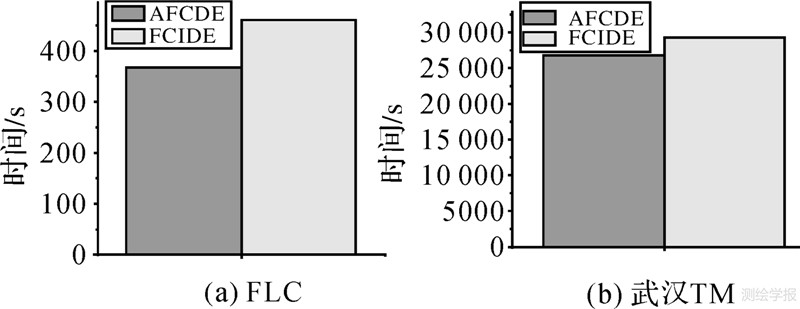
因此,将以上步骤的所有时间复杂度为O(l·N·NP·G)。其中,G为总的进化代数。文中试验部分FCIDE算法与AFCDE算法的运行时间对比如图 6所示。
|
| 图 6 AFCDE与FCIDE算法计算时间对比 Fig. 6 Comparison of time consuming between FICDE and AFCDE |
图 6(a)和图 6(b)分别为FLC数据以及武汉TM影像分类试验时,FCIDE算法与AFCD算法的运行时间对比。由图 6可知,在进行分类试验时,AFCDE算法耗时小于FCIDE算法。这是因为AFCDE算法通过局部搜索增进了搜索的效率,减少了总迭代次数,所以算法效率优于FCIDE算法。
5 结 论利用差分进化搜索效率高、效果稳定、操作简便的特点,本文提出的算法采用自适应策略对差分进化的参数进行优化,摆脱了传统方法在进行参数选择时需要经验的状况;同时,本算法将XB指数作为优化的适应度值,通过给个体添加掩膜的方式,实现了遥感影像类别个数的自动选择。通过试验表明,本文算法能够在自动寻找类别数目的同时,合理地寻找到每类的聚类中心。该算法与传统聚类算法相比不仅能够获得更高的分类精度,而且具有较高的稳定性。本文提出的算法以XB指数作为唯一的聚类有效性指标,在未来的工作中,将考虑采用多个聚类有效性指标(如XB值、Jm值等)作为适应度函数,利用多目标优化算法进行同时优化[25],进一步提升自动聚类方法的稳定性。
| [1] | LAHA A, PAL N R, DAS J. Land Cover Classification Using Fuzzy Rules and Aggregation of Contextual Information through Evidence Theory [J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(6): 1633-1641. |
| [2] | GHOSH A, MISHRA N S, GHOSH S. Fuzzy Clustering Algorithms for Unsupervised Change Detection in Remote Sensing Images [J]. Information Sciences, 2011, 181(4): 699-715. |
| [3] | WANG Xuhong, GUO Jianming, JIA Baijun, et al. Mixed Pixels Classification of Remote Sensing Images Based on Cellular Automata [J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 42-48.( 王旭红, 郭建明, 贾百俊, 等. 元胞自动机的遥感影像混合像元分类[J]. 测绘学报, 2008, 37(1): 42-48.) |
| [4] | JAIN A K. Data Clustering: 50 Years beyond k-means [J]. Pattern Recognition Letters, 2010, 31(8): 651-666. |
| [5] | BALL G H, HALL D J. A Clustering Technique for Summarizing Multivariate Data [J]. Behavioral Science, 1967, 12(2): 153-155. |
| [6] | MAULIK U, SAHA I. Automatic Fuzzy Clustering Using Modified Differential Evolution for Image Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(9): 3503-3510. |
| [7] | CANNON R L, DAVE J V, BEZDEK J C, et al. Segmentation of a Thematic Mapper Image Using the Fuzzy c-Means Clustering Algorithm [J]. IEEE Transactions on Geoscience and Remote Sensing, 1986, GE-24(3): 400-408. |
| [8] | LIU Xiaofang, HE Binbin, LI Xiaowen. Classification for Beijing-1 Micro-satellite's Multispectral Image Based on Semi-supervised Kernel FCM Algorithm [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 301-306. (刘小芳,何彬彬,李小文. 基于半监督核模糊c均值算法的北京一号小卫星多光谱图像分类[J]. 测绘学报,2011,40(3):301-306.) |
| [9] | DAS S, ABRAHAM A, KONAR A. Automatic Clustering Using an Improved Differential Evolution Algorithm [J]. IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 2008, 38(1): 218-237. |
| [10] | DAS S, KONAR A. Automatic Image Pixel Clustering with an Improved Differential Evolution [J]. Applied Soft Computing, 2009, 9(1): 226-236. |
| [11] | ZHONG Y F, ZHANG L P. A New Fuzzy Clustering Algorithm Based on Clonal Selection for Land Cover Classification [J]. Mathematical Problems in Engineering, 2011: 21. |
| [12] | OMRAN M, ENGELBRECHT A P, SALMAN A. Particle Swarm Optimization Method for Image Clustering [J]. International Journal of Pattern Recognition and Artificial Intelligence, 2005, 19(3): 297-322. |
| [13] | STORN R, PRICE K. Differential Evolution: A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces [J]. Journal of Global Optimization, 1997, 11(4): 341-359. |
| [14] | DAS S, SUGANTHAN P N. Differential Evolution: A Survey of the State-of-the-art [J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4-31. |
| [15] | XIE X L, BENI G. A Validity Measure for Fuzzy Clustering [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(8): 841-847. |
| [16] | PAKHIRA M K, BANDYOPADHYAY S, MAULIK U. A Study of Some Fuzzy Cluster Validity Indices, Genetic Clustering and Application to Pixel Classification [J]. Fuzzy Sets and Systems, 2005, 155(2): 191-214. |
| [17] | SEMNANI A, REKANOS I T, KAMYAB M, et al. Two-dimensional Microwave Imaging Based on Hybrid Scatterer Representation and Differential Evolution [J]. IEEE Transactions on Antennas and Propagation, 2010, 58(10): 3289-3298. |
| [18] | YANG G Y, DONG Z Y, WONG K P. A Modified Differential Evolution Algorithm with Fitness Sharing for Power System Planning [J]. IEEE Transactions on Power Systems, 2008, 23(2): 514-522. |
| [19] | CONG A, CONG W, LU Y, et al. Differential Evolution Approach for Regularized Bioluminescence Tomography [J]. IEEE Transactions on Biomedical Engineering, 2010, 57(9): 2229-2238. |
| [20] | BOUSSA D I, CHATTERJEE A, SIARRY P, et al. Hybridizing Biogeography Based Optimization with Differential Evolution for the Optimal Power Allocation in Wireless Sensor Networks [J]. IEEE Transactions on Vehicular Technology, 2011, 60(5): 2347-2353. |
| [21] | ROCCA P, OLIVERI G, MASSA A. Differential Evolution as Applied to Electromagnetics [J]. IEEE Antennas and Propagation Magazine, 2011, 53(1): 38-49. |
| [22] | ZHONG Yanfei, ZHANG Liangpei, LI Pingxiang. Fuzzy Cluster Validation for Remote Sensing Image Classification[J]. Geomatics and Information Science of Wuhan University, 2009, 34(4): 391-394. (钟燕飞,张良培,李平湘. 遥感影像分类中的模糊聚类有效性研究[J]. 武汉大学:学报信息科学版,2009, 34(4): 391-394.) |
| [23] | MAULIK U, BANDYOPADHYAY S. Genetic Algorithm-based Clustering Technique [J]. Pattern Recognition, 2000, 33(9): 1455-1465. |
| [24] | BREST J, GREINER S, BOSKOVIC B, et al. Self-adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems [J]. IEEE Transactions on Evolutionary Computation, 2006, 10(6): 646-657. |
| [25] | BANDYOPADHYAY S, MAULIK U, MUKHOPADHYAY A. Multiobjective Genetic Clustering for Pixel Classification in Remote Sensing Imagery [J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5): 1506-1511. |