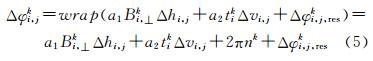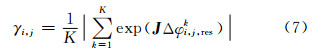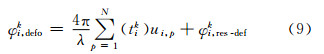2. 防灾科技学院防灾工程系,河北 三河065201
2. Department of Diseaster Prevention Engineening,Institute of Disaster Prevention, Sanhe 065201,China
基于重复轨道的差分合成孔径雷达干涉测量(differential interferometric SAR,DInSAR)技术始于1989年[1],由于在测量1992年Landers地震形变场[2, 3]的成功应用而受到广泛关注。但是,该技术易受空间失相干、时间失相干[4]和大气干扰[5]等因素的影响,难以进行常态化的实际应用。为了克服D-InSAR技术的这些限制,自20世纪90年代末,一些时间序列InSAR技术被提出。它们总体上可以概括为两类:以永久散射体干涉(permanent scatterer[6, 7, 8]、persistent scatterer interferometry[9]或PS-InSAR)为代表的单一主影像时间序列InSAR技术和以小基线集技术(small baseline subset interferometry或SBAS InSAR)[10, 11, 12]为代表的多主影像时间序列InSAR技术。时间序列InSAR技术对上述3种制约因素均有良好的免疫力,目前已经取代传统的D-InSAR技术在火山、地震、滑坡等领域得到大量应用[13, 14, 15, 16]。由于城市地区拥有密集的天然点目标,时间序列InSAR技术在城市地面沉降测量方面已经逐步实现工程化应用。国外最典型的例子是欧空局的Terrafirma项目[17]。在国内,时间序列InSAR技术也被应用于多个城市的地面沉降监测[18, 19, 20, 21, 22, 23]。
但是,时间序列InSAR技术中仍有一些问题有待完善,其中之一就是形变模型。现有的时间序列InSAR处理中,都将形变模式假设为以线性形变为主,然后在后续处理中再恢复出残余的非线性形变分量。事实上,当点目标的形变呈现高度的非线性且在空间不相关的时候,形变反演结果会有很大误差[7]。目前国内外关于形变模型的研究较少,文献[24—26]曾采用三角函数模型对一类特殊的形变——周期性形变进行了研究[24, 25, 26]。本文将对现有时间序列InSAR处理中的形变模型问题展开研究。首先从原理上分析线性形变模型的不足;然后根据魏尔斯特拉斯逼近定理,提出基于多项式的形变模型,并给出相应的时间序列InSAR形变解算方法;最后介绍多项式形变模型的试验结果及分析。
1 线性形变模型解算的原理分析 1.1 时间序列InSAR相位模型时间序列InSAR处理中,第i个点目标上的干涉相位(假定地形相位已经通过已有的DEM除去了)可以表示为[7, 8]
式中,wrap(·)表示相位缠绕算子;φik表示点目标上的干涉相位观测值;φi,atmok表示大气不均匀引起的干涉相位;φi,orbk为基线误差引起的干涉相位;φi,topo-resk为DEM残差引起的干涉相位;φi,noisek表示失相干噪音。φi,topo-resk与DEM残差Δhi之间具有线性关系[8] 式中,Bi,⊥k是第k个干涉图的垂直基线距,系数a1由该点的斜距、入射角以及雷达波长决定。地表位移引起的干涉相位φi,defok可以分解为线性形变相位和非线性形变相位,如下式所示 式中,vi为线性形变速率;tik为第k个干涉图的影像时间差。这样,干涉相位模型可进一步表示为 式中,非线性形变相位Δφi,,non-lineark、基线误差相位φi,orbk和大气相位φi,atmok都具有较强的空间相关特性,通过两个相邻点目标i、j间的相位差分运算可以基本消除这3项的贡献,此干涉相位差为 式中,Δhi,j表示两点目标间的高程残差之差;Δvi,j表示两点目标间的线性形变速率之差异;nk为相位缠绕因子,残差相位 是相邻点目标间的大气贡献相位、基线误差相位、非线性沉降相位和噪声贡献相位的差分之和。联立全部干涉图(假设共有K个)上i、j点目标间的如式(5)所示的干涉相位差方程可以组成一个方程组,形成时间序列InSAR的干涉相位模型。 1.2 相位模型的求解原理干涉相位模型是一个不定方程组,没有确定解。求解方法有二维周期图法[7]和空间搜索法[11, 23]。二者在本质上等价的[11],都是基于以下的时态相干因子取得最大值来确定得到了Δhi,j、Δvi,j的最佳解
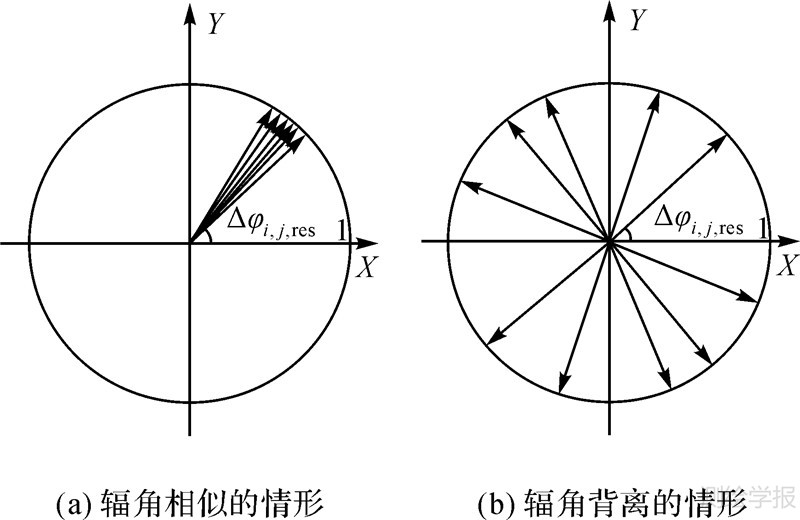
式中,J为虚数单位。这个求解方法的原理是:时态相干因子对应着复平面内K个单位矢量之和,当这些单位矢量有相似的幅角主值时(如图 1(a)所示),其矢量和有较大的模,极限情况是这些矢量的辐角主值Δφi,j,resk 完全相等,此时γi,j取得最大值1;当这些辐角主值完全背离时(如图 1(b)所示),这些矢量相加可能相互抵消,当完全抵消时γi,j取得最小值0。辐角主值相似意味着相位方程解的取值Δhi,j,Δvi,j使相位模型与观测值的契合度最佳。
|
| 图 1 K个单位矢量相加 Fig. 1 K unit vectors summation |
上述求解原理隐含着一个重要的假设,即
只有这个条件成立,Δφi,j,resk才能成为单位矢量exp(JΔφi,j,resk)的幅角主值,而不仅是幅角。若式(8)不满足,如Δφi,j,resk=1.5π,则按照式(6)使干涉相位残差等于1.5π的一组解(Δhi,j,Δvi,j)和使干涉相位残差等于-0.5π的另一组解将取得同样的γi,j值,此时利用时态相位相干因子最大化得到的模型解将不唯一。因此,式(8)是干涉相位模型能够得到唯一最佳解的一个关键必要条件。同时,从图 1可以看到,相位模型得到唯一最佳解的另一个必要条件是:在所有干涉图上的相邻点目标残差相位Δφi,j,resk的值相近。这个条件在时间序列InSAR处理中通常被当做检验点目标质量的判据,即将相位模型解算出的Δhi,j、Δvi,j代回式(6)可以计算出每个干涉图的残差相位Δφi,j,resk,所有干涉图上的残差相位的标准差必须小于某个预设的阈值。如果某一对相邻点目标的残差相位不满足此条件,则可判断其中的一个点目标质量不高,须将此点去掉[18] 。一般情况下,式(8)是容易满足的。按式(6)定义的残差相位的4个分量中,由于点目标的特性,噪声相位很小。 由于大气相位和基线误差相位的高度空间相关性,邻近点的Δφi,j,atmok及Δφi,j,orbk也会很小。 但是,如果真实形变的非线性非常强烈,则相邻点目标之间的非线性形变相位之差可能会较大,从而导致条件式(8)不满足。这就是形变模型的重要性之所在,也是线性形变模型的主要弱点。
2 时间序列InSAR的多项式形变模型 2.1 多项式形变模型的表达针对上述的以线性为主的形变模型的不足,提出如下多项式形变模型
式中,ui,p分别对应着N阶多项式形变模型中的线性速率、加速度、三次速度项等;φi,res-defk表示N阶多项式模拟后的残余形变引起的干涉相位。 这个改进的形变模型基于著名的魏尔斯特拉斯逼近定理[27]:在有界区间上定义的任何连续函数,在此区间内都可以用多项式一致逼近。而地面形变完全可以看成是一个定义于研究时段上的连续函数。因此,从理论上它可以被多项式一致逼近。相应的,两个邻近点目标i、j之间的干涉相位之差可表示为
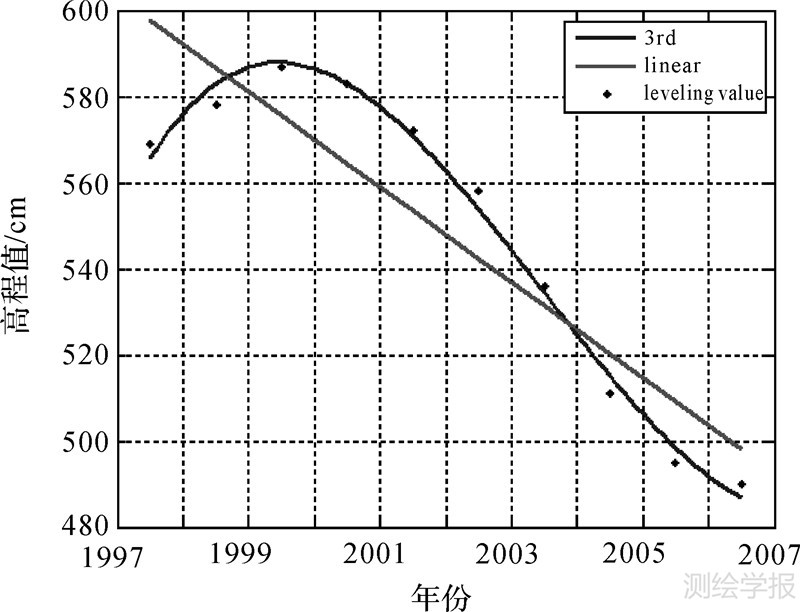
式中,残差相位Δφi,j,resk为由于多项式模型能比线性模型更精确地逼近真实形变,式(9)中的残余形变相位φi,res-defk将会是一个很小的量,因而此时的残差相位将更容易满足式(8)。 图 2显示某水准点观测到的1997—2006年间的地面沉降量(每年1个记录),以及分别用一次多项式和三次多项式进行拟合的状况。对于这种非线性比较明显的形变,相邻点目标之间的非线性形变相位之差可能较大,从而导致式(8)不成立。而用高次多项式对形变过程进行模拟,由于残余形变相位会很小,则会确保式(8)成立从而得到正确的模型解。
|
| 图 2 某水准点测量到的地表形变时间序列及分别用一次多项式和三次多项式进行拟合的结果 Fig. 2 Subsidence measurement records from 1997 to 2006 of a leveling point, and the fitting curves using the linear and 3rd polynomial respectively |
采用多项式形变模型后,干涉相位方程中的形变参数从线性形变速率差扩展为N阶多项式的系数Δui,j,1,…,Δui,j,N。解算方法也可以采用类似的空间搜索法。首先通过关于形变和DEM精度的先验知识给定待求解参数的变化范围,然后让待求解参数(Δui,j,1,…,Δui,j,N,Δhi,j)在各自的变化范围内按照一定的步长进行遍历,对每一组取值计算由式(7)定义的时态相干因子γi,j,对应于γi,j最大值的取值即为待求参数的最佳解。
计算完相邻点目标之间形变模型参数和高程残差之间的增量Δui,j,1,…,Δui,j,N,Δhi,j后,利用一个形变状态和高程残差已知的点作为参考点,通过基于不规则三角网建立的最小二乘增量集成方法[22]或以时态相干因子作为权重的加权平均法[11]可以计算得到每一个点目标的多项式形变模型和高程残差的绝对量。然后,需要对残余形变相位和大气相位进行估计。PS-InSAR和SBAS InSAR对此步骤采用的是非常相似的处理,详细处理可参考文献[7, 11, 19]。
3 应用实例分析以山西省太原市地面沉降为例,进行多项式形变模型的应用研究。所用的SAR数据为2003-08-17—2009-02-01的23景ENVISAT ASAR影像,具体时间和空间基线分布见表 1。 研究区范围为太原市,覆盖面积约为40 km×30 km=1200 km2(图 3(a))。
| 成像日期 | 时间基线/d | 垂直基线/m | |
| 1 | 2003-08-17 | 0 | 0 |
| 2 | 2003-11-30 | 105 | 725 |
| 3 | 2004-01-04 | 140 | 1252 |
| 4 | 2004-05-23 | 280 | 1005 |
| 5 | 2004-10-10 | 420 | 971 |
| 6 | 2004-11-14 | 455 | 111 |
| 7 | 2005-01-23 | 525 | 496 |
| 8 | 2005-02-27 | 560 | 627 |
| 9 | 2005-07-17 | 700 | 1425 |
| 10 | 2005-08-21 | 735 | 944 |
| 11 | 2006-02-12 | 910 | 208 |
| 12 | 2006-11-19 | 1190 | 33 |
| 13 | 2007-01-28 | 1260 | 153 |
| 14 | 2007-03-04 | 1295 | 967 |
| 15 | 2007-05-13 | 1365 | 483 |
| 16 | 2007-09-30 | 1505 | 431 |
| 17 | 2007-11-04 | 1540 | 851 |
| 18 | 2007-12-09 | 1575 | 156 |
| 19 | 2008-01-13 | 1610 | 611 |
| 20 | 2008-02-17 | 1645 | 206 |
| 21 | 2008-08-10 | 1820 | 883 |
| 22 | 2008-12-28 | 1960 | 603 |
| 23 | 2009-02-01 | 1995 | 336 |

|
| 图 3 太原市区23景ASAR影像的振幅平均图像以及反演的三次多项式形变模型 Fig. 3 The average amplitude and the 1st, 2nd and 3rd order coefficients of the polynomial deformation model |
太原市是我国最缺水的省会城市之一,大规模的地面沉降开始于20世纪70年代,20世纪80年代为地面沉降快速发展阶段,形成了4个沉降中心,90年代地面沉降持续急剧扩张,进入21世纪,地面沉降呈现出不均衡发展的态势[28]。
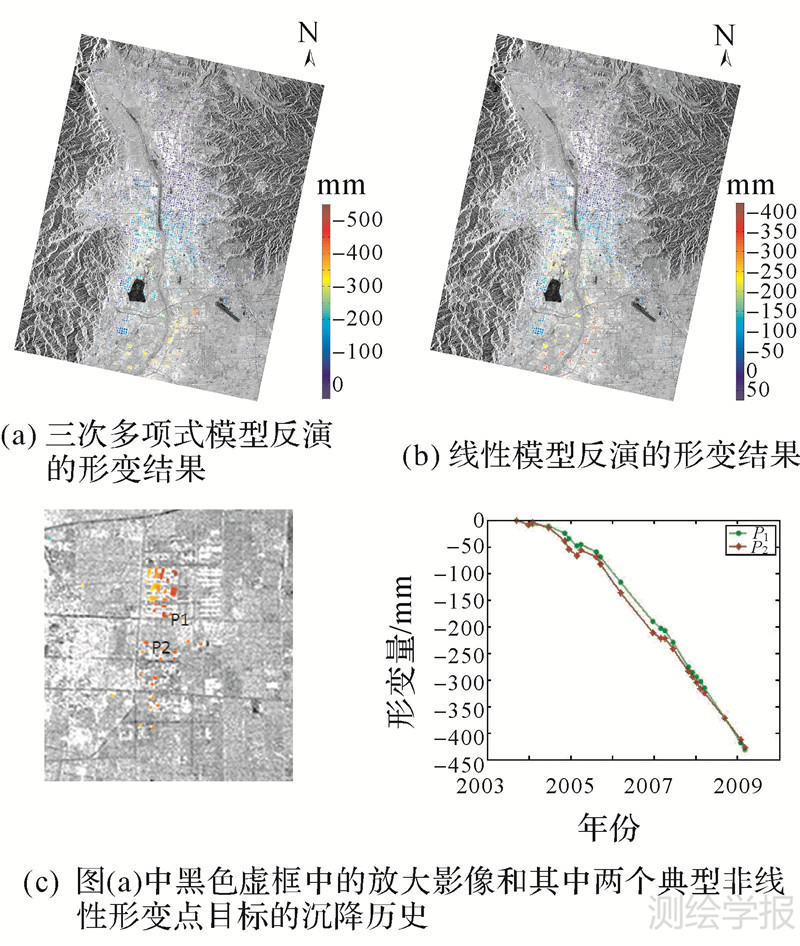
采用小基线集InSAR技术反演太原市地表形变。按照时间间隔小于3年、垂直基线小于400 m的原则,形成了93个小基线干涉图。利用SRTM DEM去除了地形相位。按照93个干涉图的相干系数平均值高于设定阈值(本例中为0.3)的条件进行点目标初选。在相邻点相位模型解算中,通过对时间序列残差相位的均方差及时态相干因子分别设定阈值(本例中设定残差相位均方差小于1.0 rad,时态相干因子大于0.7),进一步去掉质量不高的点目标。为了对比分析,分别采用三次多项式形变模型和线性模型进行了计算,两种方法进行高相干点相位模型解算的时间分别为296.3 min及92.7 min。图 3(b)、(c)、(d)分别显示了不同阶多项式系数值(分别对应于线性速率、加速度、三次速度项)。将三阶多项式形变和残余形变累加在一起可以得到点目标在整个时段内的平均形变速率或累计形变量。图 4(a)、(b)分别显示了采用两种形变模型得到的总形变量。比较发现,采用线性形变模型,最终获得8111个点目标,而三次模型得到了8755个点目标。如图 4(a)下部黑色虚线方框中包含的点目标(形变量均在400 mm以上),线性模型方法都没有检测出来。为了进一步说明,将图 4(a)黑色虚线方框区域及其中两个点目标的沉降历史一并显示在图 4(c)中。可以看出,这两个点的形变演化曲线均呈现明显的非线性。在采用线性形变模型的解算中,这些点因其残差相位不满足条件式(8)无法得到正确的模型解而被去掉了。三次形变模型能更精确地模拟这些点的形变,因此能正确解算出这些点的形变量。另一方面,两种模型中绝大部分点重合的事实也表明,研究区内绝大部分点目标的形变状况符合线性模型。
|
| 图 4 太原市区2003—2009年累计形变量对比 Fig. 4 The comparison of cumulative subsidence of Taiyuan from 2003 to 2009 derived from linear and 3rd polynomial deformation models respectively |
为了进行定量的精度评价,利用从太原市有关部门得到的30个红色水准点(如图 3(a)所示)2004—2006年的实测沉降数据为参考,将两种模型分别得到的同一时段内的形变量(已投影到竖直方向)进行了比较,结果列于表 2。可以看到,仅在5个点(第5、6、13、15、30号点),三次多项式模型得到的形变量稍不如线性模型得到的形变量准确,而在其他的点目标上,三次多项式模型都更准确,在某些点目标上(如第16、21、26号点),三次多项式模型更是大幅提高了形变测量的精度。 从这30个水准点上统计,线性模型的形变中误差为6.11 mm,而三次模型的中误差缩小到了3.17 mm。
| 水准 点号 |
水准形变 测量值 |
基于三次多 项式模型的 形变结果 |
误差 | 基于线性 模型的形 变结果 |
误差 |
| P1 | 1 | 2.46 | 1.46 | 5.95 | 4.95 |
| P2 | 7 | 5.34 | -1.66 | 11.53 | 4.53 |
| P3 | 8 | 7.06 | -0.94 | 10.26 | 2.26 |
| P4 | -4 | -0.43 | 3.57 | 1.64 | 5.64 |
| P5 | 10 | 5.6 | -4.4 | 8.45 | -1.55 |
| P6 | 22 | 19.08 | -2.92 | 23.38 | 1.38 |
| P7 | 6 | 10.09 | 4.09 | 11.85 | 5.85 |
| P8 | 8 | 6.81 | -1.19 | 10.65 | 2.65 |
| P9 | 13 | 15.69 | 2.69 | 19.18 | 6.18 |
| P10 | -7 | -3.75 | 3.25 | -1.26 | 5.74 |
| P11 | -4 | -4.65 | -0.65 | -1.86 | 2.14 |
| P12 | -31 | -28.26 | 2.74 | -27.79 | 3.21 |
| P13 | -76 | -78.20 | -2.2 | -74.03 | 1.97 |
| P14 | -6 | -5.75 | 0.25 | -3.49 | 2.51 |
| P15 | -1 | -5.85 | -4.85 | -5.48 | -4.48 |
| P16 | -58 | -58.61 | -0.61 | -49.54 | 8.46 |
| P17 | -53 | -47.56 | 5.44 | -47.11 | 5.89 |
| P18 | -8 | -6.38 | 1.62 | -9.82 | -1.82 |
| P19 | -34 | -38.65 | -4.65 | -39.22 | -5.22 |
| P20 | -100 | -94.40 | 5.6 | -92.89 | 7.11 |
| P21 | -38 | -41.82 | -3.82 | -59.40 | -21.4 |
| P22 | -15 | -14.03 | 0.97 | -10.17 | 4.83 |
| P23 | -104 | -102.62 | 1.38 | -97.24 | 6.76 |
| P24 | -27 | -23.41 | 3.59 | -18.86 | 8.14 |
| P25 | -94 | -97.79 | -3.79 | -85.87 | 8.13 |
| P26 | -134 | -129.68 | 4.32 | -122.35 | 11.65 |
| P27 | -133 | -129.65 | 3.35 | -125.20 | 7.8 |
| P28 | -131 | -130.89 | 0.11 | -123.60 | 7.4 |
| P29 | -17 | -20.28 | -3.28 | -19.18 | -2.18 |
| P30 | -16 | -17.99 | -1.99 | -15.44 | 0.56 |
| 均方根误差 | 3.17 | 6.11 | |||
理论上,高阶多项式总能比低阶的多项式更精确地逼近时间序列观测值。但这不意味着在时间序列InSAR形变监测中,多项式形变模型的阶数越高越好。模型阶数越高,相位模型中需要求解的未知数越多,求解中容易出现解的发散,而且计算速度也会大大降低。在对研究区的形变状况有一定先验知识的情况下,可以根据该区典型的形变曲线确定合适的多项式阶数,阶数等于该形变曲线的拐点数加1。 一般情况下,认为三阶多项式是一个稳健的选择。但是,对于如文献[25]所研究的周期性形变,必须采用正弦或余弦函数模型。在采用更高阶的形变模型时,如何进行模型参数的稳定、快速求解是未来需要进一步研究的问题。
| [1] | GABRIEL K,GOLDSTEIN R M,ZEBKER H A.Mapping Small Elevation Changes over Large Areas:Differential Radar Interferometer[J].Journal of Geophysical Research,1989,94(B7):9183-9191. |
| [2] | MASSONNET D,ROSSI M,CARMONA C,et al.The Displacement Field of the Landers Earthquake Mapped By Radar Interferometry[J].Nature,1993,364:138-142. |
| [3] | ZEBKER H A,ROSEN P A,GOLDSTEIN R M,et al.On The Derivation of Coseismic Displacement Fields Using Differential Radar Interferometry:The Landers Earthquake[J].Journal of Geophysical Research,1994,99:19617-19634. |
| [4] | ZEBKER H A,VILLASENOR J.Decorrelation in Interferometric Radar Echoes[J].IEEE Transactions on Geoscience and Remote Sensing,1992,30:950-959. |
| [5] | ZEBKER H A,ROSEN P A,HENSLEY S.Atmospheric Effects in Interferometric Synthetic Aperture Radar Surface Deformation and Topographic Maps[J].Journal of Geophysical Research,1997,102:7547-7563. |
| [6] | FERRETTI A,PRATI C,ROCCA F.Permanent Scatterers in SAR Interferometry[C]//Proceedings of IEEE Geoscience and Remote Sensing Symposium 1999.Hamburg:IEEE,1999:1528-1530. |
| [7] | FERRETTI A,PRATI C,ROCCA F.Non-Linear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,2000,38:2202-2212. |
| [8] | FERRETTI A,PRATI C,ROCCA F.Permanent Scatterers in SAR Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,2001,39:8-30. |
| [9] | HOOPER A,ZEBKER H,SEGALL P,et al.A New Method for Measuring Deformation on Volcanoes and Other Natural Terrains Using Insar Persistent Scatterers[J].Geophysical Research Letters,2004,31(23):611. |
| [10] | MORA O,MALLORQUI J J,DURO J,et al.Long-term Subsidence Monitoring of Urban Areas Using Differential Interferometric SAR Techniques[C]//Proceedings of IEEE Geoscience and Remote Sensing Symposium 2001.Sydney:IEEE,2001:1104-1106. |
| [11] | MORA O,MALLORQUI J J,BROQUETAS A.Linear and Nonlinear Terrain Deformation Maps from a Reduced Set of Interferometric SAR Images[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41:2243-2253. |
| [12] | BERARDINO P,FORNARO G,LANARI R,et al.A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential Interferograms[J].IEEE Transactions on Geoscience and Remote Sensing,2002,40:2375-2383. |
| [13] | BERARDINO P,CASU F,FORNARO G,et al.Small Baseline DIFSAR Techniques for Earth Surface Deformation Analysis[C]//Proceedings of Fringe Workshop 2003.Franscati:[s.n.],2003. |
| [14] | PAPOUTSIS I,KONTOES C,MASSINS B A,et al.Assessing The Pre-Seismic and Post-Seismic Displacement in The Athens Metropolitan Area by SAR Interferometric Point Target Analysis,Using ERS and Envisat Datasets[C]//Proceedings of Fringe Workshop 2009.Frascati:[s.n.],2009. |
| [15] | FARINAA P,COLOMBOB D,FUMAGALLIB A,et al.Permanent Scatterers for Landslide Investigations:Outcomes from The ESA-SLAM Project[J].Engineering Geology,2006,88:200-217. |
| [16] | VILARDO G,VENTURA G,TERRANOVA C,et al.Ground Deformation Due to Tectonic,Hydrothermal,Gravity,Hydrogeological,and Anthropic Processes in the Campania Region (Southern Italy) from Permanent Scatterers Synthetic Aperture Radar Interferometry[J].Remote Sensing of Environment,2009,113:197-212. |
| [17] | ADAM N,PARIZZI A,EINEDER M,et al.Practical Persistent Scatterer Processing Validation in the Course of the Terrafirma Project[J].Journal of Applied Geophysics,2009,69:59-65. |
| [18] | ZHANG Yonghong,ZHANG Jixian,GONG Wenyu,et al.Monitoring Urban Subsidence Based on SAR Interferometric Point Target Analysis[J].Acta Geodaetica et Cartographica Sinica,2009,38(6):482-487.(张永红,张继贤,龚文瑜,等.基于SAR干涉点目标分析技术的城市地表形变监测[J].测绘学报,2009,38(6):482-487.) |
| [19] | WU Tao,ZHANG Hong,WANG Chao,et al.Retrieval of Urban Slow Deformation by Using Mutibaseline DInSAR Technique[J].Chinese Science Bulletin,2008,53(15):1849-1857.(吴涛,张红,王超,等.多基线距DInSAR技术反演城市地表缓慢形变[J].科学通报,2008,53(15):1849-1857.) |
| [20] | GONG Huili,ZHANG Youquan,LI Xiaojuan,et al.Research on The Land Subsidence of Beijing Based on PS-InSAR Technology[J].Progress in Natural Science,2009,19(11):1261-1266.(宫辉力,张有全,李小娟,等.基于永久散射体雷达干涉测量技术的北京市地面沉降研究[J].自然科学进展,2009,19(11):1261-1266.) |
| [21] | HE Xiufeng,ZHONG Haibei,HE Min.Ground Subsidence Detection of Nantong City Based on PS-InSAR and GIS Spatial Analysis[J].Journal of Tongji University:Natural Science,2011,39(1):129-134.(何秀凤,仲海蓓,何敏.基于PS-InSAR和GIS空间分析的南通市区地面沉降监测[J].同济大学学报:自然科学版,2011,39(1):129-134.) |
| [22] | LIU Guoxiang,CHEN Qiang,DING Xiaoli.Detecting Ground Deformation with Permanent-Scatterer Network in Radar Interferometry:Algorithm and Testing Results[J].Acta Geodaetica et Cartographica Sinica,2007,36(1):13-18.(刘国祥,陈强,丁晓利.基于雷达干涉永久散射体网络探测地表形变的算法与实验结果[J].测绘学报,2007,36(1):13-18.) |
| [23] | FAN Jinhui,GUO Huadong,GUO Xiaofang,et al.Monitoring Subsidence in Tianjin Area Using Interferogram Stacking Based on Coherent Targets[J].Journal of Remote Sensing,2008,12(1):111-118.(范景辉,郭华东,郭小方,等.基于相干目标的干涉图叠加方法监测天津地区地面沉降[J].遥感学报,2008,12(1):111-118.) |
| [24] | LANARI R,LUNDGREN P,MANZO M,et al.Satellite Radar Interferometry Time Series Analysis of Surface Deformation for Los Angeles,California[J].Geophysical Research Letters,2004,31:613. |
| [25] | KAMPES B M,HANSSEN R F.Ambiguity Resolution for Permanent Scatterer Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(11):2446-2453. |
| [26] | COLESANTI C,FERRETTI A,NOVALI A,et al.SAR Monitoring of Progressive and Seasonal Ground Deformation Using the Permanent Scatterers Technique[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41(7):1685-1701. |
| [27] | KLAMBAUER G.Mathematical Analysis[M].ZHUANG Yadong,Translate.Shanghai:Shanghai Science and Technology Press,1983.(G.克莱鲍尔.数学分析[M].庄亚东,译.上海:上海科学技术出版社,1983.) |
| [28] | YAN Shilong,WANG Yanxin,MA Teng,et al.Mechanism and simulation of land subsidence in the Cenozonic inland faulted basin:a case study of Taiyuan City,Shanxi Province,China[M].Wuhan:China University of Geosciences Press,2006.(闫世龙,王焰新,马腾,等.内陆新生代断陷盆地区地面沉降机理及模拟-以山西省太原市为例[M].武汉:中国地质大学出版社,2006.) |