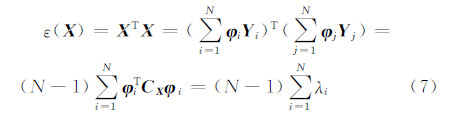2. 北京师范大学遥感科学国家重点实验室，北京 100101；
3.武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079；
4. 卫星海洋环境动力学国家重点实验室，浙江 杭州 310012
2.State Key Laboratory of Remote Sensing Science, Beijing Normal University,Beijing 100101, China;
3. State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
4. State Key Laboratory of Satellite Ocean Environment Dynamics, Hangzhou 310012, China
1 引 言
合成孔径雷达(synthetic aperture radar,SAR)图像会受到其自身固有的相干斑噪声的影响，相干斑噪声严重影响图像的质量，给图像的自动解译造成很大的困难[1]。因此，相干斑抑制成为SAR图像处理的关键步骤，也是后继SAR图像特征提取、分割、识别的基础。为了有效去除相干斑噪声，国内外学者进行了大量的研究，分别提出了基于核独立成分分析[1]、基于线性多通道最优滤波求和[2]以及基于小波分解[3, 4]等多种SAR图像滤波算法。利用经验模态分解(empirical mode decomposition,EMD)进行相干斑抑制为SAR图像去噪提供了一种新的思路[5, 6]，EMD是文献[7]提出的一种新的时频分析工具，此方法将信号分解成有限个内蕴模态函数(intrinsic mode function，IMF)和一个均值趋势函数之和。EMD通过筛选的迭代程序来取得基底IMF，IMF会随信号的不同而改变，它是一组完全数据驱动的自适应基底，不需要事先设定基底和分解层数。近年来，EMD算法被逐渐应用到了SAR图像的相干斑抑制中，并取得了很好的去噪效果。文献[8—10]对含乘性噪声的SAR图像进行4个方向的EMD分解，根据边缘所在的方向从IMF中选择相应数据进行部分重构，有效地去除了相干斑噪声；文献[11—12]应用EMD分解对相干条纹噪声进行了有效去除；文献[13]利用EMD对SAR的干涉相位图像进行分解，然后通过部分重构的方法有效去除了干涉相位图像中的相干斑噪声；文献[14]应用复数EMD(complex EMD,CEMD)同时分解SAR图像实部和虚部，根据阈值确定噪声项IMF，对非噪声项IMF进行部分重构以去除窄带相干噪声，也取得了很好的去噪效果。
在文献[8—14]的EMD相干斑抑制算法中，都是采用部分重构的方法进行。在部分重构去噪算法中，对EMD分解后的前几项IMF认为全部由噪声构成直接去除，对剩下的IMF进行累加重构，以达到去噪的目的。文献[15]研究表明，含噪信号经EMD分解后，前几项IMF中仍含有较多的细节信息，而且在后面的IMF中也分布有不同程度的噪声，因此采用直接部分重构的方法对SAR图像去噪时，会损失大量的细节信息，噪声也不能得到彻底的去除。为了克服EMD部分重构去噪算法的不足，本文采用PCA对SAR图像的IMF作进一步处理，提出了一种改进的EMD部分重构去噪算法。首先利用PCA对SAR图像的IMF进行分解，然后根据IMF中所含噪声的能量自适应选择合适的主分量重构IMF，进一步去除IMF中的噪声；最后对处理后的所有IMF进行累加重构，得到去噪SAR图像。
2 经验模态分解
经验模态分解算法基于以下假设：任何信号都是由一系列幅度和相位都随时间变化的基本模式分量构成，这种基本模式分量必须满足两个条件，即它的零点数与极点数相等或至多相差1个，以及由它的极大值和极小值确定的上下包络线关于时间轴局部对称,文献[7]将这种基本模式分量定义为内蕴模态函数，EMD方法可以将多分量信号的各阶IMF分别筛选出来。信号x(t)经 EMD分解后x(t)可表示为[2]：x(t)=
+rN(t)，其中dj表示内蕴模态函数IMF；N表示内蕴模态函数IMF的个数；rN是分解后的余项。如果x(t)是一个被高斯白噪声污染的信号，则经EMD分解后噪声主要集中在前几项IMF中[10]。
将SAR图像进行对数变换并进行均值调整后，乘性相干斑噪声近似变为零均值的加性高斯白噪声[16]。设对数SAR图像为I0，设I0经EMD分解后，第k层IMF为imfk=[d1 d2 … dN]，定义imfk的能量ε(imfk)为
式中，N表示imfk的长度。为了方便讨论，令fk=imfk，假设fk=gk+Vk，其中gk表示fk中所包含的信号成分；Vk表示fk中的噪声成分。设Vk的能量为ε(Vk)，根据含噪信号经EMD分解后的噪声能量模型[17]，可对imfk中噪声的能量ε(Vk)进行近似计算
式中，β≈0.719；ρ≈2.01。但简单的令ε(V1)=ε(imf1)，不考虑imf1中所含的细节信息，会导致噪声能量估计偏大，不利于信号细节信息的保留。本文首先利用PCA对imf1进行去噪，再估计各层IMF中噪声的能量。 3.2 利用PCA对各层IMF进行去噪
对数SAR图像经EMD分解后，各层IMF中都含有不同程度的噪声，希望利用PCA进一步去除各层IMF中的噪声。记
则CX=E{(X－mX)(X－mX)T}为fk的协方差矩阵。设λ1≥λ2≥…≥λN是CX的特征值，φ1、φ2、…、φN是对应的特征向量，记Φ=[φ1 φ2 … φN]T，则Φ是一个正交矩阵。定义 Y=[Y1 Y2 … YN]T=Φ(X－mX)，根据PCA的分解特性可知，X中的噪声分布在所有的成分分量Yi中，而信号主要集中在前几层的成分分量中。如果选择前H个特征向量构成新的变换矩阵 ΦH=[φ1 φ2 … φH 0 … 0]T，定义新的变换YH=ΦH(X－mX)，则通过反变换，可以由YH得到原信号X的近似值
因此，
即为fk去噪后的信号，而从fk中删除的噪声为
在利用PCA去除imfk中噪声时，必须要选择合适个数的成分分量进行重构，通常根据前H个主成分的累计贡献率
来确定保留的成分分量的个数。但成分分量的选择并不是一个简单的事情：累计贡献率r取得太大，会残留较多的噪声，导致噪声不能完整的去除；累计贡献率r取得太小，又会损失较多的信号细节信息。本文通过imfk中所含噪声的能量，自适应的确定对imfk去噪时应保留的主分量个数。
3.2.1 利用PCA对imf1去噪时主分量的选择方法
由EMD对噪声信号的分解特性可知[17, 18]，imf1基本由噪声构成，只含有少量的信号细节信息，该类信号经PCA分解后，信号基本只集中在第一个成分分量中[19, 20]。因此本文中在利用PCA对f1进行去噪时，仅保留第一个主成分分量进行重构。即令X=f1，X利用PCA去噪后的信号为
，此时从X中所删除的噪声为
从而可求出f1中所含噪声的能量ε(V1)=ε(ΔX)。根据EMD分解中噪声能量分布模型式(2)和ε(V1)的值，可对fk(k≥2)中所含噪声的能量进行计算。 3.2.2 利用PCA对imfk(k≥2)去噪时主分量的选择方法
以下讨论利用PCA对fk(k≥2)进行去噪时，主成分分量的选择方法。如果在PCA重构时，通过选择合适的H，使得式(3)中删除的噪声ΔX的能量与fk中所包含噪声Vk的能量相同，也即在选择H时，使得 ε(ΔX)=ε(Vk)，则可认为噪声被全部去除，保留下来的主成分分量就是理想的不含噪声的信号gk。 为了方便计算并减小误差，对上式进行一定的变形，上式等价于
由式(3)可知，所删除的噪声ΔX的能量为 而信号X的能量为
因此在利用PCA对fk进行去噪时，如果选择前H个主成分分量进行重构，则删除的噪声ΔX的能量与原信号X的能量之比为
。从式(5)可知，为了使删除的噪声的能量与fk中所含噪声的能量相等，应选择合适的H，使得
，此时可认为fk中的噪声全部被去除，剩余部分不再含有噪声，全部由信号信息组成。但在选择H时，很难保证使得恰好成立，本文中对H按照以下方法进行取值,如果存在β使得式(8)成立，则令H=β
3.3 基于PCA的EMD相干斑抑制的步骤
本文提出的联合PCA和EMD进行相干斑抑制的步骤如下。
步骤1 计算SAR图像I的边缘方向[8]。
步骤2 对I进行对数变换和均值处理，设处理后的对数SAR图像为IL。
步骤3 对IL按照4个方向分别进行EMD分解，对各分解结果按以下方式进行去噪：① 令X=fk，求X协方差矩阵CX的特征根λ1≥λ2≥…≥λm 和对应特征向量{φi}；② 对于f1，取H=1，进行重构去噪得到f1d，根据式(4)计算f1 中噪声的能量ε(V1)，并根据公式(2)估计fk(k≥2)中的噪声能量ε(Vk)；③ 对于fk(k≥2)，根据式(8)、式(15)确定H值，进行重构去噪得到fkd；④ 令imfkd=fkd，则imfkd即为imfk去噪后的结果，对imfkd(k≥1)进行累加重构，得到去噪后的对数图像。
步骤4 对4个方向去噪后的对数图像进行指数变换，结合边缘方向计算最终去噪图像Id。
4 试验结果及分析
为了客观评价SAR图像的相干斑抑制效果，本文采用以下3个标准对去噪结果进行评价[21]：① 等效视数(ENL)；② 均值比MR；③ 边缘保持指数ESI。为了验证本文算法的有效性，试验中采用两幅SAR图像作为测试图像：英国Bedford-shire地区，X波段，2视SAR图像，大小为 256像素×256像素图 1(a)；来自美国Sandia国家实验室的3视X-SAR图像，大小为512像素×512像素图 2(a)。 在试验中，分别采用传统的EMD部分重构去噪算法 (conventional EMD partial reconstruction,EMD-CPR )[17]、改进的EMD阈值去噪算法 (clear iterative EMD interval-thresholding,EMD-CIIT)[15]和本文方法(improve EMD partial reconstruction,EMD-ICPR)进相干斑抑制。在EMD-ICPR算法中，对各层IMF进行PCA处理时，采用以下方式：对IMF进行分块PCA分解;采用文献[19]中的方法进行训练样本集选择,试验中去噪模块的尺寸设为6×6，样本集训练模块的尺寸设为30×30。图 1(a)和图 2(a)由不同算法去噪后的结果分别如图 2(b)～图 2(d)和3(b)m～图 3(d)所示。
|
| 图 1 SAR图像1相干斑抑制结果 Fig. 1 Speckle reduction comparison of SAR image 1 |
|
| 图 2 SAR图像2相干斑抑制结果 Fig. 2 Speckle reduction comparison of SAR image 2 |
从图 1和图 2的视觉效果上分析可知，EMD-CPR方法去噪后，边缘保持较好，比较清晰，但有大量噪声未能去除而且有较多的细节信息损失；EMD-CIIT方法的去噪效果要好于传统部分重构算法，在噪声去除和细节保持两方面都有较好改进。EMD-ICPR方法得到的结果的整体清晰度更高，与EMD-CIIT的去噪结果相比可以看出：EMD-ICPR方法在平滑区域噪声去除的更彻底；在边缘和纹理细节区域细节损失更少，较多的细小边缘都能够被保留，而EMD-CIIT的去噪结果中，一些细小的边缘和纹理无法得到有效保持。为了定量对比各个算法的抑制平滑效果，在图 1(a)和图 2(a)中分别选择3个同质区域，图 1(a)中所选区域的大小为25像素×25像素、35像素×35像素、50像素×50像素，图 2(a)中所选区域的大小为59像素×93像素、46像素×72像素、25像素×33像素，计算去噪后这些区域的ENL，试验结果由表 1所示。由表 1的试验数据可知，EMD-ICPR方法对同质区域相干斑的抑制能力最优，与EMD-CPR算法相比ENL平均提高约60.474，与EMD-CIIT相比平均提高约22.462。
|
| 原始图像 | 2.884 | 3.226 | 2.743 | 8.324 | 8.165 | 9.104 |
| EMD-CPR | 28.622 | 61.322 | 33.327 | 55.897 | 44.859 | 59.455 |
| EMD-CIIT | 31.757 | 73.390 | 99.426 | 94.362 | 89.436 | 110.876 |
| EMD-ICPR | 62.149 | 91.524 | 108.214 | 123.367 | 117.327 | 143.443 |
试验结果的均值比MR和边缘保持指数ESI分别由表 2和表 3给出。从表 2和表 3中的数据可知，EMD-ICPR方法去噪后，图像的均值比也是最优，很好地保持了图像的辐射特性，与EMD-CPR和EMD-CIIT相比，MR分别平均降低了0.136和0.076；而且EMD-ICPR方法去噪后的SAR图像，在水平和垂直方向的边缘保持指数ESI均高于另外两种方法，与EMD-CPR相比ESI平均提高了0.122 8，与EMD-CIIT相比边缘保持指数ESI平均提高0.056 7。这说明本文方法在消除噪声的同时，有效地保持了图像的边缘细节信息。通过以上分析可以看出，不论是从视觉效果，还是从定量的客观评价指标来看，EMD-ICPR方法都具有一定的优势，与现有EMD去噪算法相比，有较好的改进。
| 均值比 | 边缘保持指数 | ||
| 水平方向 | 垂直方向 | ||
| EMD-CPR | 1.245 | 0.4388 | 0.4846 |
| EMD-CIIT | 1.116 | 0.4993 | 0.5428 |
| EMD-ICPR | 1.043 | 0.5745 | 0.6135 |
| 理想值 | 1.000 | 1.0000 | 1.0000 |
| 均值比 | 边缘保持指数 | ||
| 水平方向 | 垂直方向 | ||
| EMD-CPR | 1.193 | 0.5349 | 0.5567 |
| EMD-CIIT | 1.104 | 0.6242 | 0.6132 |
| EMD-ICPR | 1.025 | 0.6534 | 0.649 |
| 理想值 | 1.000 | 1.0000 | 1.0000 |
EMD分解是一种完全数据驱动的自适应多尺度分解算法，与传统的多尺度分解如金字塔或小波分解不同，EMD不需要预先给定基地和分解层数，而是根据数据本身特性自适应地确定基地和分解层数，特别适用于非线性、非稳态数据的分析与处理。本文分析和研究了对数SAR图像经EMD分解后各层IMF中噪声的分布特性和噪声能量的估计方法，给出了利用PCA对各层IMF进行去噪处理时主成分分量的选择方法，在此基础上提出了一种改进的EMD相干斑抑制方法。本文方法在一定程度上克服了EMD部分重构去噪算法细节信息损失较大且噪声不能完全去除的缺点，通过两组SAR图像进行了试验比较，结果表明本文提出的利用PCA和EMD进行相干斑抑制的方法具有良好的去噪效果。由于EMD分解是一个迭代计算的过程，计算复杂度较高，因此本文提出的相干斑抑制算法的计算效率较低，在今后的研究中如何采用并行算法提高计算效率是一个重要问题。此外，由于EMD方法本身的理论还不成熟，如何从理论上证明对数SAR图像的IMF中噪声仍为加性噪声，并结合试验构造IMF系数比较精确的分布模型，也是今后EMD相干斑抑制中需要重点研究的问题。
| [1] | ZHANG Zhongshan, YU Jie, YAN Qin, et al. Research on Polarimetric SAR Image Speckle Reduction Using Kernel Independent Component Analysis[J]. Acta Geodaetica et Cargographica Sinica, 2011, 40(3):290-295.(张中山, 余洁, 燕琴, 等. 基于核独立成分分析的极化SAR图像相干斑抑制[J]. 测绘学报, 2011, 49(3): 290-295.) |
| [2] | YANG Shenbing, LI Bingbai, SHEN Shuanghe, et al. Structure Retaining Linear Multi-channel SAR Image Speckle Filter[J]. Acta Geodaetica et Cargographica Sinica, 2006, 35(4):364-370. (杨沈斌,李秉柏,申双和,等. 基于特征保持的线性多通道最优求和SAR图像滤波算法. 测绘学报, 2006, 35(4):364-370.) |
| [3] | ZHANG Jun, LIU Jian. A Speckle Reduction Algorithm by Soft-thresholding Based on Wavelet Filters for SAR Images[J].Acta Geodaetica et Cargographica Sinica, 1998, 27(2):119-124.(张俊,柳健. SAR图像斑点噪声的小波软门限滤除算法[J]. 测绘学报, 1998, 27(2): 119-124.) |
| [4] | STIAN S, ELTIFT T. A Stationary Wavelet-Domain Wiener Filter for Correlated Speckle[J]. IEEE Transactions on Geosciences and Remote Sensing, 2008, 46(4):1219-1230. |
| [5] | ELGAMEL S A, SORAGHAN J. Empirical Mode Decomposition-Based Monopulse Processor for Enhanced Radar Tracking in The Presence of High-Power Interference[J]. LET Radar, Sonar and Navigation, 2011,5(7):769-779. |
| [6] | OLUFEMI A, VLADIMIR A, AUROOP R. Empirical Mode Decomposition Technique With Conditional Mutual Information for Denoising Operational Sensor Data[J]. IEEE Sensors Journal, 2011,11(10):2565-2575. |
| [7] | HUANG NE, SHEN Z, LONG SR, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[C]//Proceedings of the Royal Society of London.London:[s.n.],1998:903-995. |
| [8] | HAN C M, GUO H D, CHANG L W, et al. A Novel Method to Reduce Speckle in SAR Images [J]. International Journal of Remote Sensing , 2002, 23: 5095-5101. |
| [9] | HAN Chunming, GUO Huadong, WANG Chanlin. Speckle Suppression Using the Empirical Mode Decomposition[J]. Journal of Remote Sensing, 2002,6(4):266-271. (韩春明,郭华东,王长林. 利用经验模态分解方法抑制SAR 斑点噪声[J]. 遥感学报,2002,6(4):266-271.) |
| [10] | HAN Chuming. The Study of SAR Image Speckle Filter[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2003.(韩春明. SAR 图像斑点滤波研究[D]. 北京:中国科学院研究生院,2003.) |
| [11] | MESSINA A, VITTAL V, HEYDT G. Nonstationary Approaches to Trend Identification and Denoising of Measured Power System Oscillations[J]. IEEE Transactions on Power Systems, 2009, 20(4):1798-1807. |
| [12] | BERNINI B, GALIZZI E, FEDERICO A, et al. Evaluation of The 1D Empirical Mode Decomposition Method to Smooth Digital Speckle Pattern Interferometry Fringes[J]. Optics and Lasers in Engineering, 2007, 45: 723-729. |
| [13] | YUE H Y, GUO H D, HAN C M, et al. A SAR Interferogr-am Filter Based on The Empirical Mode Decomposition Method[J]. Geoscience Remote Sensing Symposium,2001,5: 2061-2063. |
| [14] | FENG Zhou, XING Mengdao, BAI Xueru, et al. Narrow-Band Interference Suppression for SAR Based on Complex Empirical Mode Decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 423-427. |
| [15] | KOPSINIS Y, MCLAUGHLI S. Development of EMD-Based Denoising Methods Inspired by Wavelet Thresholding[J]. IEEE Transactions on Signal Processing, 2009, 57(4):1351-1362. |
| [16] | HUA X, LELAND E P, FAWWZA T U. Statistical Properties of Logarithmically Transformed Speckle[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(3):721-727. |
| [17] | FLANDRIN P, RILLING G, GONCALVES P. Empirical Mode Decomposition as a Filter Bank[J]. IEEE Signal Processing Letters, 2004, 11(2): 112-114. |
| [18] | WU Z , HUANG N E. A Study of The Characteristics of White Noise Using The Empirical Mode Decomposition Method[C]//Proceedings of the Royal Society of London.London:[s.n.],2004:1597-1611. |
| [19] | ZHANG Lei, RASTISLAV L, WU Xiaolin. PCA-based Spatially Adaptive Denoising of CFA Images for Single-sensor Digital Cameras[J]. IEEE Transactions on Image Processing, 2009,18(4): 797-812. |
| [20] | MURESAN D D, PARKS T W. Adaptive Principal Components and Image Denoising[C]//Proceedings of International Conference on Image Processing.[S.l.]:IEEE,2003:14-17. |
| [21] | HUANG Shiqi, LIU Daizhi. Research on Method and Application of Speckle Noise Reduction of SAR Image[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3): 245-250.(黄世奇, 刘代志. SAR图像斑点噪声抑制方法与应用研究[J]. 测绘学报, 2006, 35(3): 245-250. |