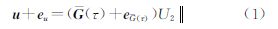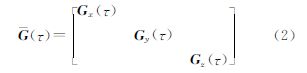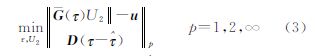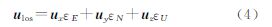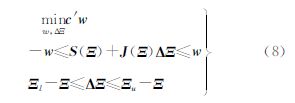2. 武汉大学 测绘学院,湖北 武汉 430079;
3. 江西省数字国土重点实验室,江西 抚州 344000
2. School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;
3. Jiangxi Province Key Lab for Digital Land,Fuzhou 344000,China
1 引 言
地震的发生通常伴随着断层位错的产生,或者说,地震的发生主要是由于介质内应变累积达到极限后介质破裂,应变能突然释放使得断层两侧发生位错。断层位错模型是地球物理模型中描述断层运动的主要模型[1, 2, 3, 4, 5]。该模型是一个复杂的非线性模型。断层参数的反演本质上是一个最优化问题,主要有线性化迭代方法和遗传算法等非线性优化算法。非线性方法由于随机策略等问题一般比较耗时,而且也有可能陷入局部极小。在线性化迭代方法中,线性化后的系数矩阵容易受到结构性扰动和误差影响。总体最小二乘方法是一种可以同时顾及系数矩阵误差和观测值误差的参数估计方法[6, 7, 8, 9, 10, 11, 12, 13]。LN算法[14, 15]是求解结构总体最小范数(structured total least norm,STLN)问题的有效方法,且该算法具有较好的收敛性;同时,在反演过程中通常也会有参数的一些先验信息,一般以参数上下界(不等式)的形式表示[16]。
InSAR测量是获取地壳形变的有效手段,其中有许多误差源影响了干涉相位测量值的质量,包括仪器噪声、轨道误差、大气干扰、时间去相关、差分干涉图中残余的地形信号以及数据处理过程中引入的误差等[17, 18]。统计学家根据大量数据指出,在生产和科学实验中,粗差的出现约占观测总数的1%~10%[19];由于记录和抄写错误、图像配准建模和基线估计中的粗差以及控制点数据和相位解缠中存在的错误,都将使InSAR获取的形变观测值存在粗差[18, 20];控制点粗差产生的原因主要有[21]成像区域存在大面积水域或光滑地面、雷达系统本身成像特点造成的透视收缩、顶底倒置、图像阴影、斑点噪声等、各种因素引起的影像去相关以及数据处理中匹配窗口选择太小等;相位解缠失败将导致不可靠的模糊度值,从而产生粗差,且无论采用何种解缠方法都可能产生粗差[20]。
2008年11月10日青海省大柴旦发生了Mw6.3级地震。本文将采用LN算法和加上模拟污染正态分布[19, 22]粗差的InSAR数据反演该地震断层位错模型参数,同时为了顾及粗差的影响采用具有抗差能力的1范数进行求解,并利用地质构造背景、已有文献对该次地震的反演结果作为先验信息。
2 断层位错模型和LN算法 2.1 Okada矩形位错模型在均匀弹性半无限介质空间中,任一断层待反演Okada矩形位错模型的10个参数为[1, 2]:3个位错分量(走滑分量U1、倾滑分量U2、张裂分量U3)、断层中心位置(a,b)、断层深d以及断层几何参数(断层长L、宽W、倾角δ、走向α)。走滑分量、倾滑分量和张裂分量都会引起相应的地表水平位移ux、uy和垂直位移uz,因此可以根据地表位移反演断层参数;反演时为了计算的方便往往需要将地表位移从地面测量坐标系(某大地测量坐标系)转换到以断层中心点为原点的断层坐标系。
2.2 断层参数反演STLN问题的LN算法下面以倾滑断层位错引起的地表位移为例说明本文采用的STLN算法。
令
τ=[dδLWabα]T
根据Okada位错模型,则有
式中,u是倾滑断层位错引起的地表位移,u=[uxuyuz]T;eu是地表位移的观测误差;eG(τ)是格林函数矩阵G(τ)的误差;G(τ)是由参数τ决定的非线性结构的格林函数,即 式中,Gx(τ)、Gy(τ)和Gz(τ)分别对应于Okada位错模型中的非线性部分。式(1)的表示方式将Okada位错模型中的参数分成了两部分:与观测值呈线性关系的参数U2和非线性关系的参数τ。未知参数τ的变化必将引起矩阵G的结构性扰动,同时该问题的线性化迭代解法如Gauss-Newton法和Levenbeg-Marquardt法需要求解G(τ)的雅可比矩阵,线性化必然使得求导得到的系数矩阵含有误差,应该将此误差与观测值误差一同考虑,由此得到该问题的结构总体最小范数(STLN)解的目标函数为
式中,D为正定对称权阵; 为参数的先验信息;p的选择取决于误差特性,当误差属于高斯或近似高斯分布时p=2,当误差未知但有界时采用最小最大估计方法可以得到好的结果取p=∞,当观测值含有少量的粗差时取p=1。
为参数的先验信息;p的选择取决于误差特性,当误差属于高斯或近似高斯分布时p=2,当误差未知但有界时采用最小最大估计方法可以得到好的结果取p=∞,当观测值含有少量的粗差时取p=1。
利用InSAR数据监测地震同震形变场,对于视线方向观测值有
式中,ulos表示InSAR在视线方向的位移观测值;ux、uy和uz分别表示地表位移在x、y和z 3个方向上的分量;εE、εN和εU表示InSAR观测值与地表位移之间的转换系数。Envisat卫星IS2波段InSAR观测值与地表位移的转换关系为[23]:在升轨时εE、εN和εU分别为-0.385、-0.068和0.921;在降轨时εE、εN和εU分别为0.385、-0.068和0.921。InSAR观测值除了包含视线方向的位移观测值外,还包括方位向观测值;方位向观测值同样与地表观测值之间存在着一定的转换关系。
因此,由式(1)、式(2)和式(4)得
式中,G(τ)=Gx(τ)εE+Gy(τ)εN+Gz(τ)εU。则InSAR数据STLN解的目标函数变为 令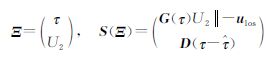
S(Ξ)的雅可比矩阵为J(Ξ),本文采用的解算STLN问题的LN算法如下[14]:
(1) 初始值:Ξ=Ξ0
(2) 迭代计算:
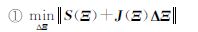
② υ=||S(Ξ)||-||S(Ξ)+J(Ξ)ΔΞ||
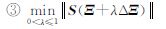
④ Ξ=Ξ+λΔΞ
⑤ 计算S(Ξ)、J(Ξ)、S(Ξ)
(3) 迭代终止:υ≤tol。
当p=2时,LN算法等价于Gauss-Newton法的线性搜索,而当p=1时,LN算法在于重复求解一个线性规划问题[15]。在求解反演问题中,一般会有一些断层参数的先验信息,常以不等式的形式给出,即
在LN算法的(2)—①中包含了可以加入式(7)的线性规划问题解,文献[15]在GiT中将这一问题通过变量代换变为求解线性规划问题,具体如下:令c′=11…1为代价向量(cost vector),线性规划问题为
因为
通过如下变量代换
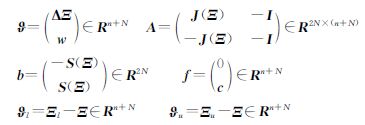
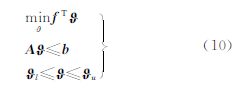
则线性规划问题式(8)变为线性规划问题的标准形式,即
3 大柴旦Mw 6.3级地震构造背景及InSAR同震位移场 3.1 地质构造背景2008年11月10日青海省大柴旦Mw6.3级地震发生在大柴旦—宗务隆山南缘断裂带上。该断裂带位于祁连地震带的南边界,由多条次级断裂组成,是夹持在西侧NE向的阿尔金大型走滑断裂与东侧NNW向的鄂拉山右旋走滑断裂带之间构造转换的过渡断裂;该断裂带长300 km,东起大柴旦北缘,经泽令沟农场、道勒根木、铅矿、过巴音河,向西经红山煤矿、库克浩尔格到夏尔恰达;该断裂带东段由3条次级断裂段组成,第四纪时期经历了多次逆冲活动[24]。
大柴旦Mw6.3级地震可能是对2008年汶川Mw8.0级地震在青藏块体内部应力调整的响应,该次地震主要以逆冲为主并兼有走滑特性[24]。综合国家地震台网中心和USGS等研究机构给出的大柴旦地震参数,发现这次地震震源深度约为10 km左右;虽然地震面波的振幅比较大,且对地表建筑有一定的破坏,但是地震断层在地表的破裂不明显[24]。根据USGS、哈佛大学等给出的地震参数,通过震源机制解分析得知[24],该次地震P轴仰角25°、方位角192°;T轴仰角59°、方位角46°,表明了该地震区域的受力是以北北东向为主,与邻近地区震源机制解反应的情况基本一致。
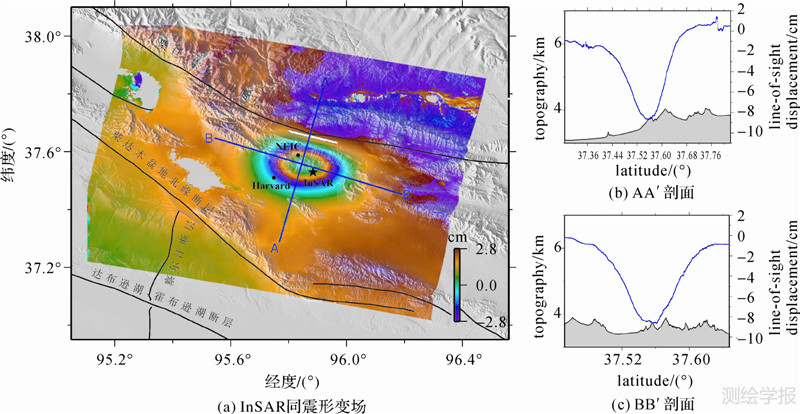
3.2 InSAR同震位移场本文所用InSAR数据为[25]:大柴旦地震发生后,项目组通过中国科技部和欧空局(ESA)联合资助的“龙计划”二期国际合作项目收集了覆盖此次地震的Envisat/ASAR雷达影像,经过筛选对比,最终选取了2008-11-05和2009-01-14的两景影像(表 1),并采用二通法来获取此次地震的同震地表形变场。本研究中所使用的InSAR处理平台为Caltech/JPL的ROI_PAC3.0.1 软件,处理过程中采用了ESA提供的DOR精密轨道来修正轨道误差以及利用90 m分辨率的SRTM DEM来去除地形影响;为进一步降低干涉相位的噪声,提高干涉图质量,采用了基于能量谱的局部自适应滤波方法对干涉图进行滤波;最后采用枝切法来解缠得到了差分干涉相位[25]。完成整个干涉处理后,得到了经过地理编码后的大柴旦地震同震形变场(图 1)。
从图 1中可以看到[25],形变区覆盖了大柴旦地震的整个震中区域;除了部分被湖泊和冰雪所覆盖区域外,整个干涉图相位连续,条纹光滑清晰,差分干涉图上出现了两个干涉条纹,表现为一个清晰的椭圆状,NNE向长35 km,NEE向长45 km。LOS向的最大位移量为8 cm,远场形变量接近于0。在InSAR差分干涉图中,同时包含有大气效应、卫星轨道、DEM误差和热噪声等多种误差,这些误差对干涉相位的影响方式和量级是各不相同的,常规的误差估计方法难以确定干涉图的误差大小。本文假定差分干涉图中的误差(主要包括大气效应和卫星轨道误差)的统计特征在整个影像中具有相同的空间结构,则可以使用1D协方差函数来描述干涉图中误差的特征(包括量级和空间尺度)[25]。从表 1中可以看出,得到的InSAR同震形变场的中误差为0.52 cm,方差-协方差衰减距离为5.9 km。为了提高反演计算效率采用四叉树采样法获得540个采样点的LOS向形变量和相应的观测矢量[25](如图 2所示)。

|
| 图 2 采样后的InSAR数据形变场 Fig. 2 The InSAR coseismic deformation field after sampling |
从干涉图的条纹分布(图 1)中可以看出,大柴旦地震的发震断层结构比较简单,因此可以采用单一断层模型来获取地震的断层几何参数。文献[25]采用单一均匀滑动模型和单纯形法来反演断层参数,通过蒙特卡洛方法的100次随机选取初始参数的反演,最终确定了反演模型的解,具体为:断层中心经度为95.884 7°、断层中心纬度为37.650 5°、断层长度为15.496 5 km、断层宽度为6.697 1 km、断层上端深度为11.859 6 km、断层下端深度为17.448 5 km、断层的方位角为107.186 6°、断层的倾角为56.566 4°、断层的滑动角为101.891 1°、断层的滑动量为0.928 7 m。本文在LN算法计算过程中以此解为参考值设置参数的范围,并将本文结果与该参考值进行比较。
已发表文献中给出的有关大柴旦地震断层参数主要有:2008年大柴旦地震震中为(95.80°E,37.55°N)[26];文献[24]给出震源深度为10 km左右,且该次地震主要以逆冲为主并兼有走滑特性,同样由断层参考值的滑动量0.928 7 m和滑动角101.891 1°计算得到该断层的倾滑分量为0.908 8 m和走滑分量为0.191 4 m。因此,为了简化计算,本文在断层参数反演时仅计算倾滑分量。
利用采样后的InSAR同震位移数据(如图 2所示)和LN算法[14]求解大柴旦Mw6.3级地震断层参数反演的STLN问题。为了显示算法处理粗差的有效性,在观测数据中人为给位移数据加上均值为0、较大标准偏差的高斯噪声作为粗差,被加粗差的观测值都是随机选取的。在反演之前首先进行坐标转换,将经纬度坐标转换成直角坐标。在坐标转换中以地震震中经度(95.884 7°E)为投影的中央子午线,在迭代过程中根据先验信息设断层参数的上下界范围分别是:10 km≤深≤25 km、50°≤倾角≤75°、10 km≤长≤30 km、5 km≤宽≤15 km、0 m≤倾滑分量≤2 m、4000 km≤中心坐标x≤4200 km、-50 km≤中心坐标y≤50 km、100°≤方位角≤130°,迭代计算次数最大值为500。为了比较粗差个数的不同对反演结果的影响,设计了多个方案,即位移观测值加上相同的粗差(均值为0、标准偏差为40 mm的高斯噪声),粗差个数分别为n=5、n=10、n=15、n=20、n=25和n=30,计算结果见表 2和图 3。另外,为了比较粗差大小的不同对反演结果的影响,设计了多个方案,即位移观测值加上相同个数(n=10)的粗差,仍以大标准偏差的高斯噪声作为粗差,均值为0,标准偏差分别为σ=40、σ=45、σ=50、σ=55、σ=60和σ=65,计算结果见表 3和图 4。
| n=5 | n=10 | n=15 | n=20 | n=25 | n=30 | 参考值 |
| d | 16.903 4 | 23.520 4 | 20.240 5 | 23.601 3 | 22.887 5 | 10.995 9 | 17.448 5 |
| δ | 61.505 6 | 58.517 4 | 55.598 0 | 50.177 5 | 65.514 1 | 50.041 4 | 56.566 4 |
| L | 19.204 5 | 11.766 3 | 11.725 0 | 23.763 4 | 10.044 3 | 22.492 5 | 15.496 5 |
| W | 9.602 3 | 5.232 8 | 5.000 2 | 5.002 1 | 5.000 2 | 11.290 9 | 6.697 1 |
| U2 | 0.920 5 | 0.894 2 | 0.342 9 | 0.890 6 | 0.796 5 | 1.151 0 | 0.908 8 |
| 经度 | 95.884 7 | 95.884 6 | 95.884 8 | 95.884 9 | 95.884 5 | 95.884 8 | 95.884 7 |
| 纬度 | 37.079 5 | 37.894 5 | 37.222 1 | 37.826 7 | 37.856 3 | 37.297 6 | 37.650 5 |
| α | 115.827 5 | 104.454 5 | 113.920 8 | 123.565 6 | 121.503 2 | 119.197 6 | 107.186 6 |
| Δ | 1.160 7 | 0.470 0 | 0.344 0 | 0.228 8 | 0.612 9 | 2.137 0 | - |
| φ | 128.645 1 | 273.902 8 | 426.848 5 | 512.561 6 | 699.740 3 | 927.360 0 | - |
| T | 1.059 7 | 1.076 9 | 1.067 9 | 1.055 2 | 1.068 9 | 1.051 7 | - |

|
| 图 3 固定粗差大小(σ=40)时断层参数的反演结果 Fig. 3 Parameter inversion results(σ=40) |
| σ=40 | σ=45 | σ=50 | σ=55 | σ=60 | σ=65 | 参考值 |
| d | 23.520 4 | 23.523 0 | 23.523 6 | 23.526 9 | 23.529 9 | 23.532 0 | 17.448 5 |
| δ | 58.517 4 | 58.459 5 | 58.439 9 | 58.534 1 | 58.581 6 | 58.499 6 | 56.566 4 |
| L | 11.766 3 | 11.823 6 | 11.835 8 | 11.863 6 | 11.885 2 | 11.936 8 | 15.496 5 |
| W | 5.232 8 | 5.258 8 | 5.257 2 | 5.269 5 | 5.286 9 | 5.332 5 | 6.697 1 |
| U2 | 0.894 2 | 0.895 5 | 0.896 1 | 0.897 4 | 0.898 7 | 0.899 6 | 0.908 8 |
| 经度 | 95.884 6 | 95.884 6 | 95.884 6 | 95.884 6 | 95.884 6 | 95.884 6 | 95.884 7 |
| 纬度 | 37.894 5 | 37.894 6 | 37.894 7 | 37.894 9 | 37.895 1 | 37.895 2 | 37.650 5 |
| α | 104.454 5 | 104.750 3 | 104.842 4 | 105.046 9 | 105.213 8 | 105.487 4 | 107.186 6 |
| Δ | 0.470 0 | 0.467 7 | 0.467 6 | 0.468 0 | 0.467 5 | 0.463 8 | - |
| φ | 273.902 8 | 306.785 1 | 339.671 2 | 372.558 2 | 405.443 6 | 438.323 9 | - |
| T | 1.076 9 | 1.049 0 | 1.029 2 | 1.085 2 | 1.061 6 | 1.060 0 | - |

|
| 图 4 固定粗差个数(n=10)时断层参数的反演结果 Fig. 4 Parameter inversion results(n=10) |
在表 2和表 3中,断层中心经度和纬度是将反演得到的直角坐标转换成经纬度坐标的。表中各符号的含义分别为:深度d(km),倾角δ(°),长度L(km),宽度W(km),倾滑分量U2(m),走向方位角α(°);Δ表示迭代计算终止时前一个目标函数1范数值与终止时目标函数1范数值的差值,即Δ=||S(Ξ)||-||S(Ξ)+J(Ξ)ΔΞ||;φ=||S(Ξ)||1表示迭代计算终止时目标函数1范数值;T(104 s)表示迭代计算所耗费的时间。
为检验观测值不含粗差情况下LN1算法求解大柴旦地震断层参数的结果,进行L1范数迭代计算500次,断层参数的上下界范围与表 2和表 3反演时相同,反演结果为:d=10.000 5 km、δ=50.311 5°、L=30.000 0 km、W=4.999 6 km、U2= 12.999 4 m、中心经度为95.884 3°、中心纬度为36.704 5°、α= 119.672 2°、Δ= 0.206 2、||S(Ξ)||1= 10.686 6,计算所需时间为1.037 6×104 s,迭代1000次的计算结果与500次的结果相差不大,在此不再列出。
5 讨论与结论虽然青藏高原恶劣的自然条件使野外调查和传统大地测量技术难以完全展开,但是在没有地面观测数据的情况下,通过文献[25]利用欧空局提供的Envisat/ASAR卫星雷达影像数据获取的2008年11月10日青海大柴旦地震同震地表形变场可以看出,该形变场表现为一个清晰的椭圆状分布,NNE向长约35 km,NEE向长约45 km,LOS向的最大位移量达到8 cm。
通过本文反演结果及已有文献[24,25]可以看出,2008年青海大柴旦Mw6.3级地震是以逆冲为主兼有少量走滑特性的地震,该次地震发生在大柴旦—宗务隆山断裂带南缘。由于该地震发生于2008年5月12日汶川地震之后的2008年11月10日,因而该次地震可能是青藏高原块体内部应力调整引起的。该次地震断层没有出露地面,将表 2中的多次反演结果取平均值得到的断层参数作为大柴旦地震的断层参数,断层深度为19.691 5 km,断层倾角为56.892 3°,断层长度为16.499 3 km,断层宽度为6.854 8 km,倾滑量为0.832 6 m,断层中心经度为95.884 7°,断层中心纬度为37.529 5°,断层走向方位角为116.411 5°。USGS给出的断层中心坐标为(95.317°,37.543°),断层埋深22 km,断层走向方位角为115°,倾角为72°;Harvard给出的断层中心坐标为(95.75°,37.51°),断层埋深27.2 km,断层走向方位角为108°,倾角为67°。在观测值含有各种粗差的情况下,本文采用LN算法在L1范数下求解STLN问题得到的大柴旦地震断层参数仍与文献[24,25]的结果符合的比较好,说明该方法是有效的,可以较好地抵抗粗差的干扰。本文计算得到的地震矩为3.108 4×1018 Nm(Mw6.295 0),与文献[25]单一均匀断层模型反演得到的地震矩3.1×1018 Nm(Mw6.294 2)相同,比Harvard给出的地震矩4.1×1018 Nm(Mw6.375 2)和USGS给出的4.0×1018 Nm(Mw6.368 0)小。具体结果比较见表 4。
| 断层参数 | 本文 | 文献[25] | USGS | Harvard |
| 深度/km | 19.691 5 | 17.448 5 | 22 | 27.2 |
| 倾角/(°) | 56.892 3 | 56.566 4 | 72 | 67 |
| 长度/km | 16.4993 | 15.496 5 | - | - |
| 宽度/km | 6.854 8 | 6.697 1 | - | - |
| 倾滑量/m | 0.832 6 | 0.908 8 | - | - |
| 中心经度/(°) | 95.884 7 | 95.884 7 | 95.317 | 95.75 |
| 中心纬度/(°) | 37.529 5 | 37.650 5 | 37.543 | 37.51 |
| 走向/(°) | 116.411 5 | 107.186 6 | 115 | 108 |
| 地震矩/(1018Nm) | 3.108 4 | 3.1 | 4.1 | 4.0 |
| 矩震级/Mw | 6.295 0 | 6.294 2 | 6.375 2 | 6.368 0 |
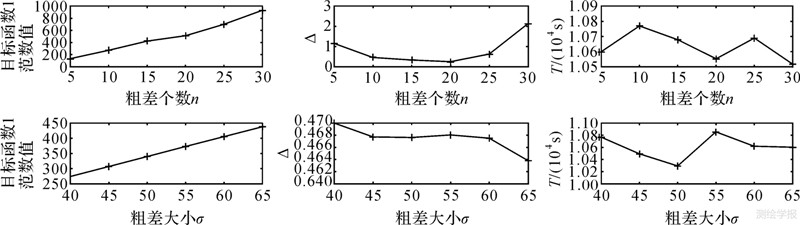
由表 2、表 3、图 3、图 4和图 5可以看出,粗差个数对参数反演结果影响比粗差大小对参数反演结果的影响大。图 3中参数上下波动比图 4中参数上下波动大,图 3中参数的连线为凸凹不平的折线,而图 4中参数的连线几乎为与横坐标(粗差大小)平行的直线。
|
| 粗实线为固定粗差大小的计算结果,计算值用“+”表示;细实线为固定粗差个数的计算结果,计算值用“+”表示;“△”表示迭代终止时与前一次迭代的目标函数1范数值之差值;“T”表示迭代计算所需的时间 图 5 迭代终止时目标函数1范数、差值和时间 Fig. 5 1 Norm and difference of objective function and time when iterations stop |
由表 2和图 5可以看出,当观测值所含粗差大小固定(σ=40)时,随着粗差个数由5个逐渐增加到30个时,迭代计算终止时目标函数的1范数值也逐渐由128.645 1增大到927.360 0,但是迭代计算所需的时间相差不大。
由表 3和图 5可以看出,当观测值所含粗差个数固定(n=40)时,随着粗差的增大(由σ=40逐渐增加到σ=65),迭代计算终止时目标函数的1范数值也逐渐由273.902 8增大到438.323 9,同样,迭代计算所需的时间相差不大。
当观测值不含粗差时,采用L1范数下用LN算法求解大柴旦Mw6.3级地震断层参数得到的结果较差,除断层走向方位角参数外,其它断层参数反演结果取值于所给的参数上下界,说明观测值仅含偶然误差时采用L1范数并不能得到最优解,只有在观测值含有粗差时采用L1范数可以取得较好的结果。
LN算法在1范数下求解断层参数的迭代计算收敛性较好。文献[14]给出了该算法收敛性的证明;LN算法充分、有效地利用各种先验信息,可以不等式约束或上下界的形式对参数进行约束。同时,该算法顾及了系数矩阵的结构性误差,是求解结构总体最小二乘问题的有效方法。
青海大柴旦地震发生之前,在大柴旦—宗务隆山断裂带及其周边发生过两次6级左右的地震,分别为2003年4月17日青海德令哈6.6级地震和2004年5月11日德令哈5.9级地震。这两次地震均发生在该断裂带的中西部,其中2003年以前的地震主要发育在断裂带的北盘,这可能意味着大柴旦—宗务隆山断裂带的地震活动向南迁移[24]。此外,近50年来,该地区进入了长时间的7级地震平静期,随着2008年汶川Mw 8.0级地震所带来的青藏块体内部的应力持续调整,青藏高原东北缘,尤其是祁连山地震带的东南部地区应该受到重点关注[25]。
| [1] | OKADA Y. Surface Deformation due to Shear and Tensile Faults in a Half-space[J].Bulletin of the Seismological Society of America, 1985,75(4):1135-1154. |
| [2] | OKADA Y.Internal Deformation due to Shear and Tensile Faults in a Half-space[J].Bulletin of the Seismological Society of America,1992,82(2):1018-1040. |
| [3] | OKUBO S.Potential and Gravity Changes due to Shear and Tensile Faults in a Half-space[J].Journal of Geophysical Research,1992,97(B5):7137-7144. |
| [4] | XU Caijun,LIU Yang,WEN Yangmao.Mw7.9 Wenchuan Earthquake Slip Distribution Inversion from GPS Measurements[J].Acta Geodaetica et Cartographica Sinica,2009,38(3):195-201.(许才军,刘洋,温扬茂.利用GPS资料反演汶川Mw7.9级地震滑动分布[J].测绘学报,2009,38(3):195-201.) |
| [5] | WANG Leyang.Research on Theory and Application of Total Least Squares in Geodetic Inversion[D].Wuhan:Wuhan University,2011.(王乐洋.基于总体最小二乘的大地测量反演理论及应用研究[D].武汉:武汉大学,2011.) |
| [6] | GOLUB G H,LOAN C F V.An Analysis of the Total Least Squares Problem[J].SIAM Journal on Numerical Analysis,1980,17(6):883-893. |
| [7] | HUFFEL S V.VANDEWALLE J.The Total Least Squares Problem:Computational Aspects and Analysis[M].Philadelphia:SIAM,1991. |
| [8] | SCHAFFRIN B.FELUS Y A.On the Multivariate Total Least-squares Approach to Empirical Coordinate Transformations: Three Algorithms[J].Journal of Geodesy,2008,82(6)373-383. |
| [9] | SCHAFFRIN B,WIESER A.On Weighted Total Least-squares Adjustment for Linear Regression[J].Journal of Geodesy,2008,82(7):415-421. |
| [10] | WANG Leyang,XU Caijun,LU Tieding.Inversion of Strain Parameter Using Distance Changes Based on Total Least Squares[J].Geomatics and Information Science of Wuhan University,2010,35(2):181-184.(王乐洋,许才军,鲁铁定.边长变化反演应变参数的总体最小二乘方法[J].武汉大学学报:信息科学版,2010,35(2):181-184.) |
| [11] | SHEN Yunzhong,LI Bofeng,CHEN Yi.An Iterative Solution of Weighted Total Least-squares Adjustment[J].Journal of Geodesy,2010,85(4):229-238. |
| [12] | TONG X H,JIN Y M,LI L Y.An Improved Weighted Total Least Squares Method with Applications in Linear Fitting and Coordinate Transformation[J].Journal of Surveying Engineering,2011,137(4):120-128. |
| [13] | XU Caijun,WANG Leyang,WEN Yangmao,et al.Strain Rates in the Sichuan-Yunnan Region Based upon the Total Least Squares Heterogeneous Strain Model from GPS Data[J].Terrestrial,Atmospheric and Oceanic Sciences,2011,22(2):133-147. |
| [14] | ROSEN J B,PARK H,GLICK J.Signal Identification Using a Least L1 Norm Algorithm[J].Optimization and Engineering,2000,1(1):51-65. |
| [15] | BIFULCO I,RAICONI G,SCARPA R.Computer Algebra Software for Least Squares and Total Least Norm Inversion of Geophysical Models[J].Computers & Geosciences,2009,35(7):1427-1438. |
| [16] | WANG Leyang,XU Caijun,WANG Jianjun.Research on Equality Constraint Inversion with Ill-posed Constraint Matrix[J].Acta Geodaetica et Cartographica Sinica,2009,38(5):397-401.(王乐洋,许才军,汪建军.附有病态约束矩阵的等式约束反演问题研究[J].测绘学报,2009,38(5):397-401.) |
| [17] | LI Zhenghong,LIU Jingnan,XU Caijun.Error Analysis in InSAR Data Processing[J].Geomatics and Information Science of Wuhan University,2004,29(1):72-76.(李振洪,刘经南,许才军.InSAR数据处理中的误差分析[J].武汉大学学报:信息科学版,2004,29(1):72-76.) |
| [18] | SONG Xiaogang,WANG Shang,XI Guangyong.Error Analysis and Reliability Theory in InSAR[J].Geotechnical Investigation & Surveying,2007(2):57-60.(宋小刚,王尚,席广永.InSAR中的误差分析和可靠性理论[J].工程勘察,2007(2):57-60.) |
| [19] | ZHOU Jiangwen,HUANG Youcai,YANG Yuanxi,et al.Robust Least Squares Method[M].Wuhan:Huazhong University of Science & Technology Press,1997.(周江文,黄幼才,杨元喜,等.抗差最小二乘法[M].武汉:华中理工大学出版社,1997.) |
| [20] | LIU Guoxiang.Mapping of Earth Deformations with Satellite SAR Interferometry:A Study of Its Accuracy and Relia- bility Performances[D].Hong Kong:Hong Kong Polytechnic University,2003. |
| [21] | HUANG Qihuan,HE Xiufeng.The Gross Error Removing Methods for Control-point Selection in SAR Registration[J].Remote Sensing Technology and Application,2007,22(1):75-78.(黄其欢,何秀凤.SAR影像配准中控制点粗差剔除方法研究[J].遥感技术与应用,2007,22(1):75-78.) |
| [22] | TUKEY W.A Survey of Sampling from Contaminated Normal Distributions[C]//Contributions to Probability and Statistics:Essays in Honor of Harold Hotelling.Standford:Stanford University Press,1960:448-485. |
| [23] | WEN Yangmao.Coseismic and Postseismic Deformation Using Synthetic Aperture Radar Interferometry[D].Wuhan:Wuhan University,2009.(温扬茂.利用InSAR资料研究若干同震和震后形变[D].武汉:武汉大学,2009.) |
| [24] | LI Zhimin,TU Hongwei,TIAN Qinjian,et al.The 2008 Mw6.3 Earthquake in the Dacaidan Region,Qinghai Province and Its Seismotectonic Setting[J].Progress in Geophys,2010,25(3):768-774.(李智敏,屠泓为,田勤俭,等.2008年青海大柴旦6.3级地震及发震背景研究[J].地球物理学进展,2010,25(3):768-774.) |
| [25] | WEN Yangmao,XU Caijun,LIU Yang,et al.Source Parame-ters of 2008 Qinghai Dacaidan Mw 6.3 Earthquake from InSAR Inversion and Automated Fault Discretization Method[J].Geomatics and Information Science of Wuhan University,2012,37(4):458-462.(温扬茂,许才军,刘洋,等.利用断层自动剖分技术的2008年青海大柴旦Mw6.3级地震InSAR反演研究[J].武汉大学学报:信息科学版,2012,37(4):458-462.) |
| [26] | LI Tao,MA Jianxin.Analysis of Earthquake Optimization Mimesis before Dacaidan Ms6.6 Earthquake[J].Plateau Earthquake Research. 2010,22(2):25-31.(李滔,马建新.大柴旦6.6级地震前的地震拟合相关系数异常分析[J].高原地震,2010,22(2):25-31.) |