2. 海岛(礁)测绘技术国家测绘局重点实验室, 山东 青岛 266510;210093
3. 中国科学院 测量与地球物理研究所,湖北 武汉 430077
2. Key Laboratory of Surveying and Mapping Technology on Island and Reef, State Bureau of Surveying and Mapping, Qingdao 266510, China;
3. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China
1 引 言
惯性导航系统(inertial navigation system) 的定位误差随时间积累发散,无法长时间保持高精度,为了满足潜艇长期隐蔽潜航的要求,有必要借助另外一种无源的辅助导航手段对INS位置进行校正。重力匹配辅助惯性导航是一种利用地球重力场特征信息对惯性导航系统位置漂移误差进行修正的导航新技术[1,2]。重力匹配辅助导航系统由惯性导航系统、重力图、重力传感器、匹配计算机等组成。载体在运动过程中,重力传感器可准实时测得重力数据,同时根据INS的位置信息,可以从重力图中读取重力数据。将这2种数据输入匹配解算计算机,利用匹配定位软件进行解算,即可求得最佳匹配位置[3, 4, 5, 6]。利用匹配位置信息对INS系统进行校正,即可起到抑制INS定位误差,延长INS重调周期的作用。重力匹配辅助惯性导航系统中代表性产品包括美国Lockheed Martin公司研制的由通用重力模块(UGM)所组成的重力导航系统(NGS)和贝尔实验室研制的重力辅助导航系统(GAINS)。
重力异常图一般是以规则格网形式预先存储在匹配计算机中,如何获取高精度、高分辨率重力异常图是进行准确匹配的关键所在。目前国内外主要采用逆Stokes公式、逆Vening-Meinesz公式对Geosat、Seasat、ERS-1和T/P等卫星测高数据进行反演获取海洋格网重力异常模型[7, 8, 9, 10],分辨率达到了2′×2′。为了进一步提高重力异常图分辨率,许多学者采用二维插值的方法对原重力异常图进行精化[11, 12],二维插值常用方法有最近邻法、最小曲率法、距离倒数加权法、多项式回归法、Kriging法、改进的Shepard方法以及径向基函数法等[13, 14]。采用函数逼近对重力异常图进行解析重构使重力异常图的应用不受分辨率限制,在重力异常函数逼近方面,相关学者也做出了大量有价值的研究[15, 16, 17, 18]。文献[15]对各种函数模型逼近及统计模型逼近的特性进行了分析,提出由函数模型逼近与统计逼近组合起来的综合逼近法,克服了2种逼近方法的不足,达到了较好的效果。文献[16]系统地建立了地球重力场逼近中的B样条表示理论和算法。文献[17]则采用快速傅里叶变换方法对局部地球重力场模型进行逼近。文献[18]提出了1种利用Fourier级数展开表示的局部地球重力场模型,该方法获得的最终解析表达式是连续的。综合来看,B样条函数逼近及傅里叶级数逼近两种方法都具有很高的精度,但由于B样条函数逼近最终解析表达式不统一,因而不适用于连续场匹配导航,而傅里叶级数逼近涉及大量参数计算,限制了连续场匹配算法实时性。高斯样条函数在医学影像、数字地形构建、计算机图形学及地球物理等领域有较为广泛的应用,文献[19]讨论了一维高斯样条在协方差函数代数确定中的应用,并对平稳随机过程逼近中一维高斯样条最优参数确定进行了研究。本文考虑到高斯函数具有局部支撑的良好特性(其函数特性与B样条函数非常接近),采用高斯函数作为样条基函数对计算区域重力异常进行二维整体逼近,因此能在保证重力异常局部特性不失真的前提下获取计算区域重力异常的统一解析式,同时考虑到高斯样条函数逼近局部重力异常的相关影响因素,采用斐波那契寻优方法获取样条函数最优参数[20]。采用高斯样条函数逼近局部重力异常运算简单且最终解析式是统一的,因此可以较好的满足了连续场匹配导航的要求,具有一定的应用价值。
2 一维高斯样条函数插值 2.1 一维高斯样条函数插值数学原理设高斯样条函数表达式为G(x)=exp(-x2/a2)。高斯函数衰减很快,它可以看作局部支撑的基函数,但它的局部支撑区间受到了参数a的控制,局部支撑区间随a增大而增大。在一维函数y=f(x)的X方向上以Δx等距采样获得离散点集合{(xi,yi)|i=1,…,n},则在X方向上的高斯样条函数表达式为 ,在已知离散点处满足插值条件:{L(xi)=f(xi)|i=1,…,n},则根据插值条件有如下线性方程:
,在已知离散点处满足插值条件:{L(xi)=f(xi)|i=1,…,n},则根据插值条件有如下线性方程:
易知A是非奇异的,即上式有唯一解,解方程即得到高斯样条函数一维插值解析式。参数a对插值影响很大,当a过小时,由于局部支撑区间很小,使得插值曲线刚度小,容易出现锯齿状;当a过大时,由于局部支撑区间很大,插值曲线刚度大,插值曲线过于平滑甚至使插值解析式在已知点的插值误差很大。由上述论述可以知道,a太大或太小均失去插值意义,因此有必要对参数a进行寻优。由上式可以看出插值由A与b唯一确定,而A由矩阵的阶数和a决定,而在求解方程的过程中存在数值计算误差,如A阶数过高或a过大,对A的求逆存在较大误差。下面计算对不同阶数和a值时A矩阵求逆数值计算误差,设I为单位矩阵,B=inv(A)A,误差计算公式如式(2),误差分析如图 1所示。

|
| 图 1 A矩阵求逆误差分析图 Fig. 1 The matrix inversion error analysis of A |
由A矩阵求逆误差分析图可以看出,当A矩阵阶数小于5或a值小于5时,A矩阵求逆运算误差较小。考虑到实际应用中对局部重力场逼近时用到的格网区域远大于5×5,这里仅对a∈[1,5]范围内进行一维变量寻优。
斐波那契数列方法是一种经典的一维寻优方法,它能以较少的迭代次数获取精度较高的最优解,且只需计算和比较函数值,算法简单易于实现,因此采用斐波那契数列方法对参数a进行寻优。为了保证插值函数与已知数据点保形性良好,采用式(3)准则函数进行寻优。
2.2 一维高斯样条函数插值仿真试验及结果分析设原函数曲线为f(x)=10sin(x)+10,x∈[0,6],以Δx=0.2在该曲线上进行等距采样获得已知离散点集,由已知数据点通过准则函数斐波那契数列寻优获得a最优值为2.8909。为说明对参数a寻优的有效性。分别令a=1、2、2.890 9、4、4.5对Δx=0.1等距离散点处进行插值并与该点原函数值相比,插值误差如图 2所示。由仿真误差分析图可以看出,当a值较小时插值曲线刚度小,在区域边缘龙格现象明显;当a较大时,曲线刚度变大,虽龙格现象得到有效抑制但整体误差变大。综合来看,取a为最优值时的插值误差及龙格现象均得到有效抑制。一维高斯样条函数插值误差数值分析结果如表 1所示,从误差分析结果可以看出a取最优值时其插值绝对误差均值及绝对误差均方差均为5组试验中的最小,从而说明对参数a进行寻优是有效的。最后采用B样条函数对已知数据进行仿真试验,从图 2及表 1可以表明采用B样条函数进行插值边缘误差较大,总体精度较好,但其精度远低于最优高斯样条函数插值。

|
| 图 2 一维高斯样条函数插值仿真误差分析图 Fig. 2 The analysis of 1-D Gauss spline interpolation simulation errors |
| 仿真试验条件 | a=1 | a=2 | a=2.890 9 | a=4 | a=4.5 | B-spline |
| 绝对误差均值 | 0.029 096 | 0.004 964 | 0.000 280 | 0.000 526 | 0.122 100 | 0.065 745 |
| 绝对误差均方差 | 0.011 166 | 0.000 236 | 0.000 002 | 0.000 000 2 | 0.010 832 | 0.063 222 |
下面在一维高斯样条函数插值基础上讨论二维高斯样条插值。已知XY平面上等分离散格网点集合{(xi,yj)|i=1,…,m;j=1,…,n}及其对应函数值zi,j(i=1,…,m;j=1,…,n),则其X方向一维高斯样条函数解析式为Lx=Span{Gx((x-xi)/Δx)},Y方向一维高斯样条函数解析式为Ly=Span{Gy((y-yj)/Δy)},XY平面的二维高斯样条函数可以写成Lx与Ly的张量积形式:
即有 不妨设 则上式可以简化为矩阵形式: 则根据插值条件{L(xi,yj)=zi,j |i=1,…,m;j=1,…,n},有如下线性方程:易知X、Y均为非奇异矩阵,即上式有唯一解,解方程即得到高斯样条函数二维插值解析式。由上一节论述可知参数a对插值影响很大,因此有必要在二维高斯样条函数插值前对X,Y方向的ax、ay进行寻优。同上考虑到求逆计算误差,仅需对ax∈[1,5],ay∈[1,5]区间内进行寻优,理论上必须对ax、ay进行二维联合寻优。考虑到二维准则函数构建复杂且需进行二重积分影响算法速度,将二维寻优模型解耦为X方向的ax寻优模型及Y方向的ay寻优模型。解耦方法为:将格网点划分为n行,对每行分别进行一维高斯样条函数插值,将这n次一维插值准则函数之和作为二维高斯样条函数插值X方向的ax寻优准则函数;将格网点划分为m列,同样对每列分别进行一维高斯样条函数插值,将这m次一维插值准则函数之和作为二维高斯样条函数插值Y方向的ay寻优准则函数;二维高斯样条函数插值准则函数解耦后表达式如式(9)、式(10)所示。根据准则函数解耦模型我们即可采用斐波那契数列方法对ax、ay分别进行寻优。
3.2 二维高斯样条函数逼近仿真试验为方便仿真验证,直接采用MATLAB里的高斯合成曲面函数peaks函数组合成局部连续重力异常场作为仿真用真实背景场,该重力异常场解析表达式如式(11),其3D示意图如图 3所示。

|
| 图 3 局部连续重力异常场3D示意图 Fig. 3 The 3D map of local continuous gravity anomaly field |
以分辨率0.2×0.2在该曲面上进行等距采样获取31×31标准离散格网点集,该区域重力异常变化范围为-51.185~86.1819mGal,在已知离散格网点集的基础上采用斐波那契数列方法以10-2精度对二维高斯样条函数插值解耦准则函数分别进行寻优得到ax的最优值为3.5391及ay的最优值为2.5272。按表 2给定的5组ax、ay值对仿真区域0.1×0.1等距离散格网点进行高斯样条函数二维插值,插值结果与对应点的函数值之差作为该点的插值误差,5组试验插值误差图如图 4所示。

|
| 图 4 二维样条函数逼近仿真误差分析图 Fig. 4 The analysis of 2D spline approximation simulation errors |
| 试验1 | 试验2 | 试验3 | 试验4 | 试验5 | |
| ax | 1 | 2.5272 | 3.5391 | 3.5391 | 4 |
| ay | 1 | 2.5272 | 2.5272 | 3.5391 | 4 |
从前4组仿真试验插值误差区域分布来看,当ax、ay值较小时,插值曲面刚度小,较大误差都分布在边缘很小的一块区域内(约1~2原始格网点宽),在内部区域的插值精度都非常高,且ax、ay值越小边缘效应明显,因此在构建整个海区的高精度重力异常基准图时,有必要剔除边缘区域的异常误差数据。由后2组仿真试验插值误差图可以看出,当ax、ay值较大时,插值曲面刚度大,虽边缘效应得到有效抑制,但在内部区域误差过大甚至导致插值算法发散。由第3组仿真试验插值误差图可以看出,当ax、ay值为斐波那契数列寻优最优值时,插值误差及边缘效应均得到有效抑制。综合来看,由于已知数据沿X方向与Y方向的数据特征不同,ax、ay一般是不等的;ax、ay取过大或过小均可能导致较大误差,因此在插值前对ax、ay进行寻优是非常有必要的。5组试验的误差分析结果如表 3所示,从误差分析结果也可以看出ax、ay取最优值时其插值绝对误差均值为5组试验中的最小,从而说明在二维高斯样条函数插值时对参数a进行解耦寻优是有效的。最后设计试验6对B样条函数二维逼近进行仿真,仿真误差分析见图 4(f)及表 3。从试验结果可以看出,采用B样条对格网数据进行函数逼近时精度较好,但与最优二维高斯样条逼近有相当大的差距,从而进一步说明了最优二维高斯样条逼近的有效性。
| 试验1 | 试验2 | 试验3 | 试验4 | 试验5 | 试验6 | |
| 包含边缘区域的插值绝对误差均值 | 0.1504 | 0.0061 | 0.0026 | 0.0503 | 229.5544 | 0.6903 |
| 剔除边缘区域的插值绝对误差均值 | 0.0270 | 0.0015 | 0.00069 | 0.0643 | 298.5817 | 0.0288 |
为了验证该方法在实际重力异常数据处理中的有效性,取范围为λ:122°E~126°E,φ:20°N~24°N,分辨率为2′×2′的卫星测高反演重力异常数据作为仿真用真实重力异常基准图进行二维高斯样条逼近计算。由于在除格网点外其它位置真实重力异常并不知道,为了方便进行逼近误差分析,采用该方域4′×4′格网处重力异常数据作为已知数据点进行二维高斯样条函数逼近,获得该范围局部重力异常基准图解析表达式,在此基础上计算2′×2′格网点处重力异常逼近值,然后与已知的2′×2′格网处重力异常值进行比对分析。如图 5(a)及图 5(b)所示,二维高斯样条函数逼近的局部重力异常基准图解析式能较好的描述这一范围的重力异常基准图。从图 5(c)、图 5(d)及对应的误差分析可以得出,试算区域4′×4′格网点处二维高斯逼近计算值绝对误差均值为0.229 6

|
| 图 5 局部重力异常基准图二维高斯逼近仿真试验 Fig. 5 The simulation of local gravity anomaly map’s approximation with 2D Gauss spline |
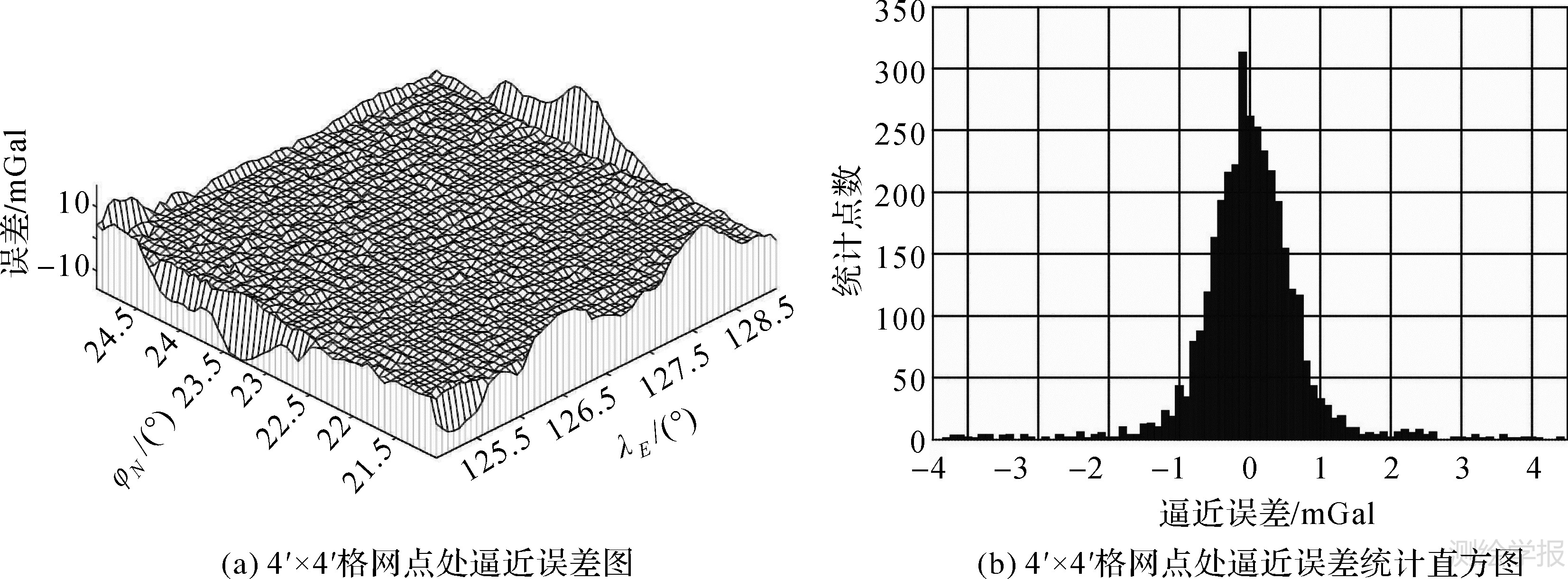
|
| 图 6 局部重力异常基准图B样条逼近仿真试验误差分析< Fig. 6 Error analysis for the simulation of local gravity anomaly map’s approximation with B-spline |
对局部离散格网重力异常场进行解析重构是研究连续场重力匹配导航的前提条件。为了适应重力匹配导航的实际应用,本文提出了利用高斯样条函数采用张量积算子对离散重力异常场进行逼近。分析表明该方法能获得局部范围内统一解析式且计算简单。需要强调的是,重力场解析重构的最终精度与原始数据分辨率及数据质量是密切相关的,而本文提出的重构方法无法消除由原始数据分辨率及其精度带来的影响。本文最后对仿真数据及实际数据进行了试算,结果表明高斯样条逼近法所获得的精度能够满足匹配导航的要求,如何在高斯样条逼近模型的基础上展开重力匹配算法解析建模有待进一步研究。
| [1] | BEHZAD K P, BEHROOZ K P.Vehicle Localization on Gravity Maps[C] //Proceedings of SPIE:3693:Unmanned Ground Vehicle Technology.[s.L.]:SPIE, 1999:182-191. |
| [2] | BISHOP C.Gravitational Field Maps and Navigational Errors[J].IEEE Journal of Oceanic Engineering, 2002, 27(3):726-737. |
| [3] | WANG Zhigang, BIAN Shaofeng.ICCP Algorithm for Gravity Aided Inertial Navigation[J].Acta Geodaetica et Cartographica Sinica, 2008, 37(2):147-157.(王志刚, 边少锋.基于ICCP算法的重力辅助惯性导航[J].测绘学报, 2008, 37(2):147-157.) |
| [4] | RICE H, MENDELSOHN L, AARONS R, et al.Next Generation Marine Precision Navigation System[C] //IEEE 2000 Position Location and Navigation Symposium.San Diego:IEEE, 2000:200-206. |
| [5] | WANG Zhigang, BIAN Shaofeng.A Local Geopotential Model for Implementation of Underwater Passive Navigation[J].Progress in Natural Science, 2008, 18(9):1139-1145. |
| [6] | XIAO Shenghong, BIAN Shaofeng.Research on Regional Model of Continuous Fourier Series of Marine Magnetic Anomaly Field Using for the Geomagnetic Navigation[C] //IIS 2010:The 2nd International Conference on International Conference on Industrial and Information System:11.Dalian:IEEE, 2010:437-440. |
| [7] | ANDERSON O, KNUDSEN P.Global Marine Gravity Field from the ERS-1 and Geosat Geodetic Mission Altimetry[J].Journal on Geophysical Ressearch, 1998, 103(C4):8129-8137. |
| [8] | HWANG C W, KAO E C, PARSONS B.Global Derivation of Marine Gravity Anomalies from Seasat, Geosat, ERS-1 and TOPEX/Poseidon Altimeter Data[J].Geophysical Journal International, 1998, 134(2):449-459. |
| [9] | SANDWELL D, SMITH W.Marine Gravity Anomaly from Geosat and ERS-1 Satellite Altimetry[J].Journal of Geophysical Research, 1997, 102(D10):10039-10054. |
| [10] | HUANG Motao, ZHAI Guojun, GUAN Zheng, et al.On the Recovery of Gravity Anomalies from Altimeter Data[J].Acta Geodaetica et Cartographica Sinica, 2001, 30(2):179-184.(黄谟涛, 翟国君, 管铮, 等.利用卫星测高数据反演海洋重力异常研究[J].测绘学报, 2001, 30(2):179-184.) |
| [11] | LI Shanshan, WU Xiaoping, ZHAO Dongming.Coons Curved Surface Reconstruction Method of Marine Gravity Anomaly Map for Navigation[J].Acta Geodaetica et Cartographica Sinica, 2010, 39(5):508-515.(李姗姗, 吴晓平, 赵东明.导航用海洋重力异常图的孔斯曲面重构方法[J].测绘学报, 2010, 39(5):508-515.) |
| [12] | WU Taiqi, HUANG Motao, LU Xiuping, JIN Jihang.Gravity Map Creating Technology in Gravity Matching Navigation[J].Journal of Chinese Inertial Technology 2007, 15(4):438-441.(吴太旗, 黄谟涛, 陆秀平, 等.重力场匹配导航的重力图生成技术[J].中国惯性技术学报, 2007, 15(4):438-441.) |
| [13] | CARLSON R E, FOLEY T A.The Parameter R2 in Multiquadric Interpolation[J].Computers Math Application, 1991, 21(9):29-42. |
| [14] | NIELSON G M, FOLEY T A, HAMANN B, et al.Visualization and Modeling Scattered Multivariate Data[J].IEEE Computer Graphics and its Applications, 1991, 11(3):47-55. |
| [15] | YANG Yuanxi, LIU Nian.A Kind of Approximation Method on Gravity Anomaly[J].Acta Geodaetica et Cartographica Sinica, 2001, 30(3):192-196.(杨元喜, 刘念.重力异常的一种逼近方法[J].测绘学报, 2001, 30(3):192-196.) |
| [16] | BIAN Shaofeng.Numerical Solution for Geodetic Boundary Value Problem and the Earth's Gravity Field Approximation[D].Wuhan:Wuhan Technical University of Surveying and Mapping, 1992:49-65.(边少锋.大地测量边值问题数值解法与地球重力场逼近[D].武汉:武汉大学, 1992:49-65.) |
| [17] | HARRISON J C, DICKINSON M.The Fourier Methods in Local Gravity Modeling[J].Journal of Geodesy, 1989, 63(2):149-166. |
| [18] | MENZ J, BIAN S.Implementing the Fourier Series as a Local Geo-potential Model in The Local Gravity Field Modeling[J].Bollettino Di Geodesia E Scienze Affini, 1998, 57(3):293-306. |
| [19] | BIAN Shaofeng, MENZ J.Determining the Parameter of a Covariance Function by Analytical Rules[J].ZFV, 1999(7):212-216. |
| [20] | OVERHOLT K J.Efficiency of the Fibonacci Search Method[J].BIT, 1973, 13(1):92-96. |













