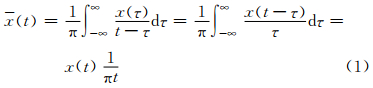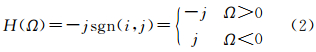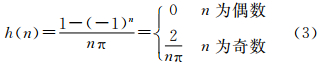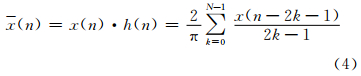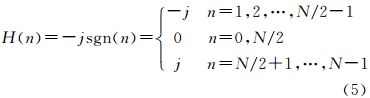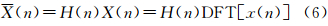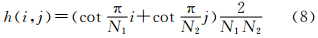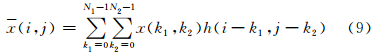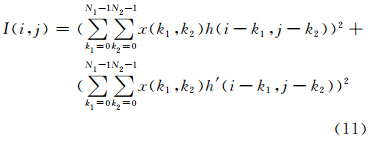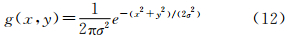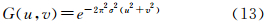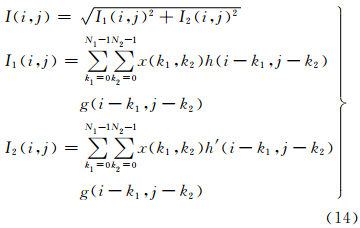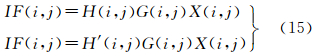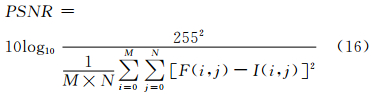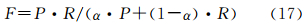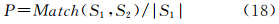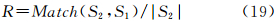2. 中国科学院 遥感应用研究所，北京 100101
2. Institute of Remote Sensing Applications, Chinese Academy of Sciences, Beijing 100101, China
1 引 言
图像边缘的检测和提取在图像处理中占据着重要地位。学者们已经提出了很多图像检测算子，如Roberts算子[1]、Sobel算子[2]，Canny算子[2]等。此外Morrone在研究马赫带中，发现相位在图像特征处具有高度的一致性，从而提出了相位一致性原理[4]。随后的研究中，Kovesi利用Log Gabor小波[5]很好地实现了图像检测[6, 7]。此外学者们在小波域[8, 9]、神经网络[10]、水平集[11]以及区间值模糊集[12]等领域也对图像边缘检测作了大量的研究。这些边缘检测方法被广泛用于各个专业领域，如遥感图像处理[13, 14]、医学图像处理[15]、面部识别[16]等领域。
希尔伯特变换被证明是一种有效的图像边缘检测的方法。Livadas和Constantinides借助一维希尔伯特变换实现图像边缘的检测和分割[17]。文献[18, 19]通过构建一维高阶伪希尔伯特变换来检测地震资料的边缘。文献[20]利用二维希尔伯特变换来检测角点[20]。
本文在一维希尔伯特变换的边缘检测基础上，提出以二维希尔伯特变换进行边缘检测工作。借由二维离散希尔伯特变换和高斯函数的频域表达，经由傅里叶变换后，生成空域检测算子。为弥补二维希尔伯特变换的方向性缺陷，通过将算子作90°旋转得到正交算子，并通过计算两算子的卷积的平方和来实现图像边缘特征的检测。其中高斯函数可以在边缘检测的过程中有效抑制图像噪声的影响。最后以DSBS图像及高空间分辨率IKONOS图像为试验数据进行边缘特征提取评价和分析。
2 希尔伯特变换 2.1 一维离散希尔伯特变换希尔伯特变换仅仅改变信号的相位值，而对信号的幅度不作任何改变。经过希尔伯特变换后，其频域信号的负频率成分作+90°相移，而正频率成分作-90°相移。设x(t)为一连续时间信号，则希尔伯特变换
(t)可定义为
由傅里叶变换可知，希尔伯特变换器h(t)=1/πt的频率响应为符号函数sgn(Ω)
对于离散时间信号x(n),希尔伯特变换器h(n)可表达为
则离散信号x(n)与希尔伯特变换器h(n)卷积得
式中，n=0,1,2,…,N-1。
由式(2)和式(4)可得
则有(n)傅里叶变换后得
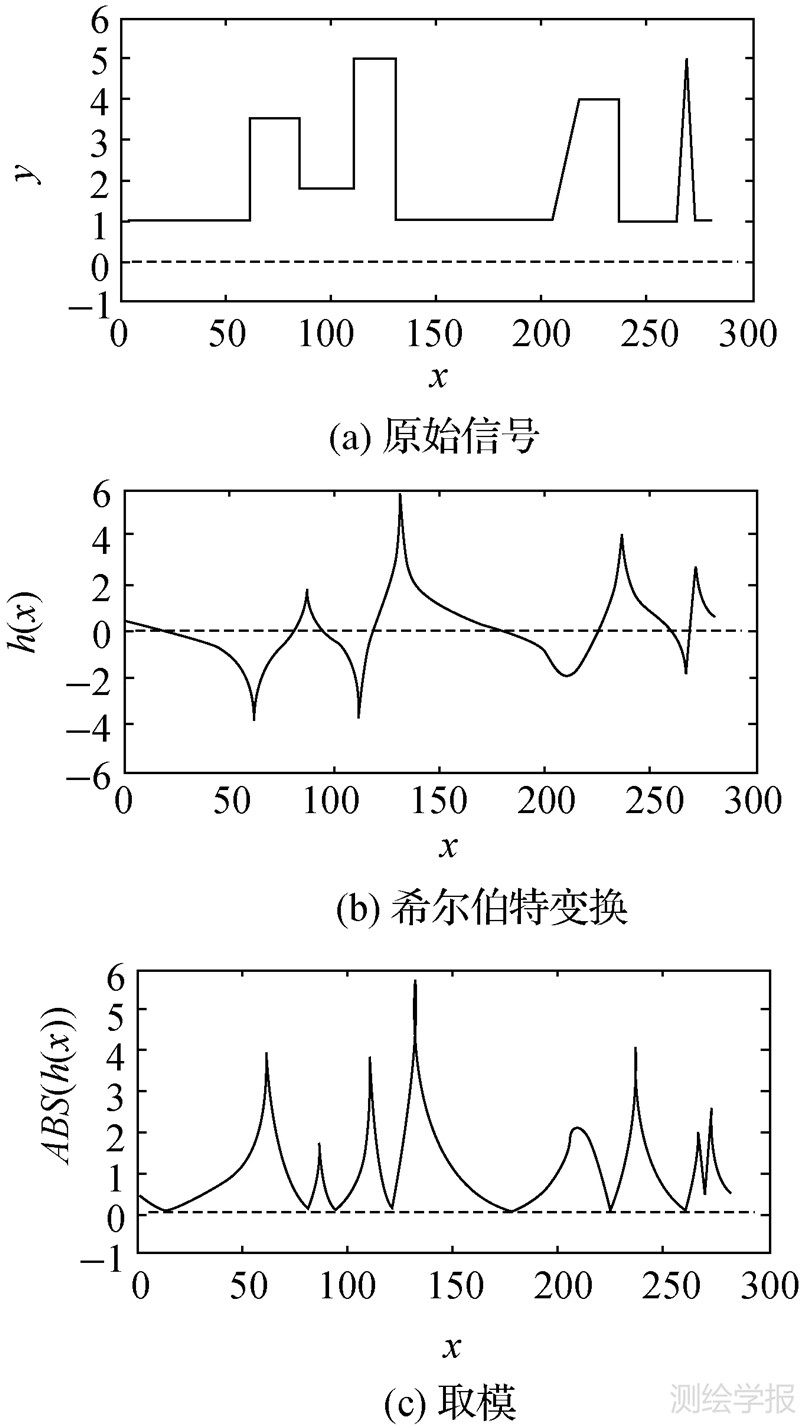
本文以一维离散信号(图 1(a))为例验证希尔伯特变换的信号边缘特征检测的效果。
|
| 图 1 信号经1-D希尔伯特变换后的结果 Fig. 1 The result of Hilbert transform of original signal |
图 1(a)为一维信号，经希尔伯特变换后得到图 1(b)，在原始信号的特征处x=60,90,115,135,210,225,240,270,275均有峰值出现，其中在梯度为负的特征处的峰值小于零。取模后得图 1(c)，灰度级差越大，则希尔伯特变换后的峰值越大。由图 1可知希尔伯特变换可用于边缘特征识别和提取。
2.2 二维离散希尔伯特变换在频域和空域中，文献[21, 22]给出了二维离散希尔伯特变换的定义。在频域中，通过定义二维离散希尔伯特变换并将其公式在频域展开来完成。对于一个N1×N2矩阵的二维信号，其二维离散希尔伯特变换定义如下
式中，Pe(i,j)和Po(i,j)均为两正交滤波器的频域表达式；Po(i,j)为奇滤波器；Pe(i,j)为偶滤波器；sgn(i,j)为符号函数；bdy(i,j) 被用来校正边界。由此H(i,j)可用来对频域图像进行希尔伯特变换。
在空域中，二维希尔伯特变换器的余切空域表达如下
式中，i=0,1,2,…，N1-1； j=0,1,2,…，N2-1。
给定图像x(i,j)，经二维傅里叶变换后，其频谱为X(i,j)。图像x(i,j)的希尔伯特变换可表达为
式中，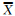
(i,j)=DFT[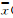(i,j)]。
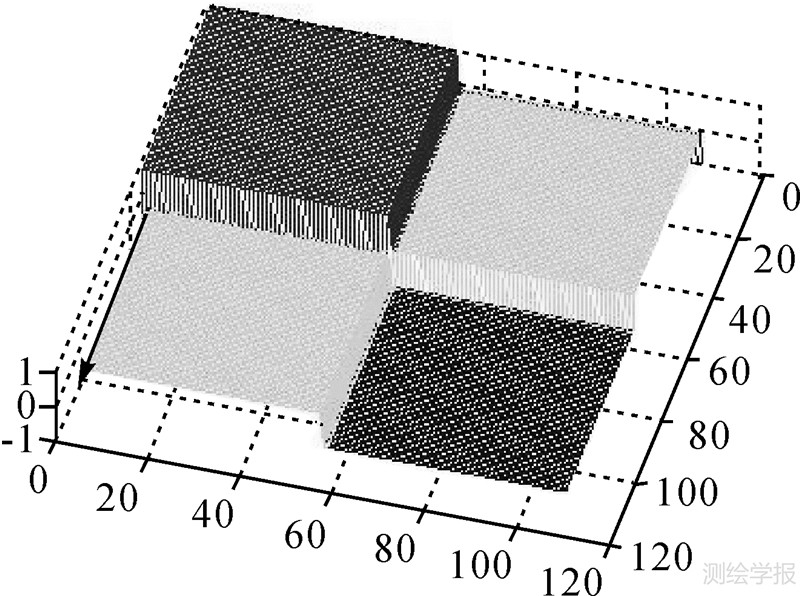
利用二维希尔伯特变换直接进行边缘检测时，检测结果具有方向性，即该方法对不同方向上分布的特征具有不同的响应值。根据二维希尔伯特变换的频域表达形式(图 2)对其进行解释。
|
| 图 2 二维离散希尔伯特变换的频域表达 Fig. 2 2-D discrete Hilbert transform in frequency domain |
在二维信号的行列数一致的前提下，空域图像的某一特征经傅里叶变换后，其频域响应分布与空域分布呈90°夹角。图 2中分布有4个区域，一个区域幅值为1，另一个幅值为-1，剩下两个区域的幅值为0。而希尔伯特变换则主要针对分布于幅值为1和-1的区域(此两区域的频域响应值呈中心对称)。
由此说明，基于二维希尔伯特变换的检测，对频域响应分布于幅值为1和-1的区域的特征具有更强的边缘响应。在检测结果中(图 3(b))，分布方向为45°左右的边缘响应值很弱，尤其是图右下角的45°分布的边缘特征。而分布方向为135°左右的边缘特征则有很强的响应。这种特点在图 3(b)中的圆环的边缘检测结果中尤为突出。
|
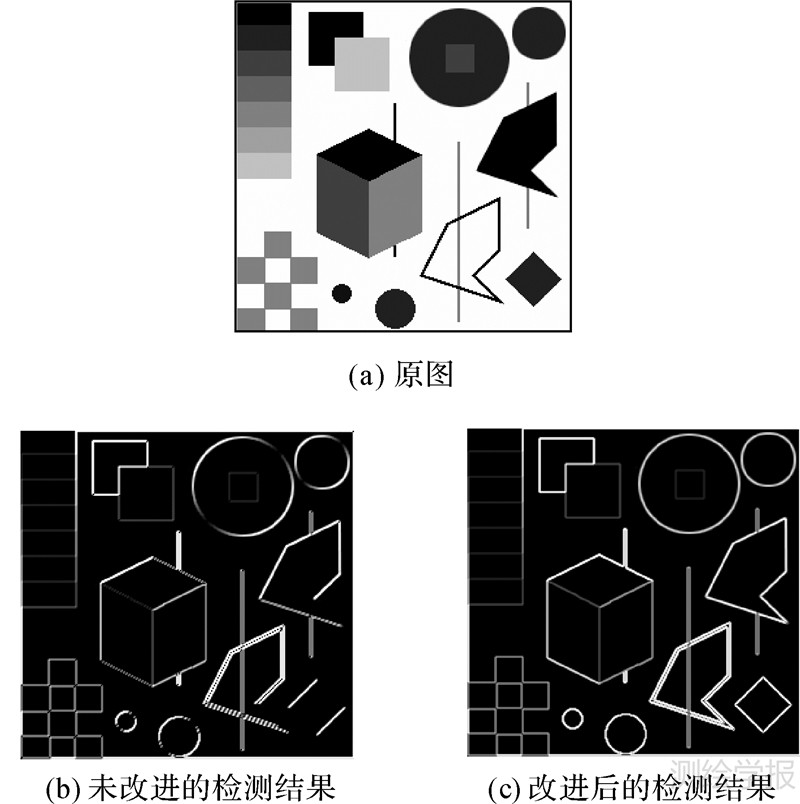
| 图 3 算法改进前后的边缘检测结果对比 Fig. 3 The comparison of the edge detection from the 2-D discrete Hilbert transform and the modified one |
因此，本文利用希尔伯特变换算子以及旋转90°后的算子之和作为边缘检测的算子，其表达式为
式中，h′为旋转90°的希尔伯特变换算子。
根据本文提出的方法，从图 3(a)所示的图像的检测结果可明显看出，经过改进后的方法(图 3(c))可以正确地提取45°方向上的边缘特征。
3.2 噪声抑制根据式(11)，可以直接对图像进行卷积运算得到边缘检测结果，但是图像和信号中的噪声无法有效地抑制。因此该方法需作进一步改进以得到更好的边缘检测效果。
Marr已经证明高斯函数与人类视觉系统非常接近的效果[23]。DoG滤波器、Canny算子等均用到高斯函数来优化边缘检测结果和抑制噪声。二维高斯函数的空域表达式为
式中，σ为标准差。经傅里叶变换后，得
式中，G(u,v)为高斯函数的频域响应，u、v分别表示水平和垂直方向的频率。
将高斯低通滤波核引入希尔伯特变换器中，可得边缘响应强度为
式中，I(i,j)为检测结果；I1(i,j)为希尔伯特算子检测结果；I2(i,j)为旋转90°的希尔伯特算子检测结果；x(i,j)为原图像。而检测结果的频域表达为
式中，IF(i,j)为频域滤波后的频谱图像；G(i,j)、H(i,j)和H′(i,j)分别为高斯函数、希尔伯特变换和旋转90°的希尔伯特变换的频域响应。
根据时域相关定理，两个频域函数相乘的结果为其相对应的空域函数的卷积结果的频域表达。所以本文利用式(14)中的H(i,j)和G(i,j)通过频域相乘后，再经傅里叶变换后生成一个算子以代替式(13)中的h(i,j)和g(i,j)，从而方便图像边缘特征的检测运算。图 4为引入高斯函数的二维离散希尔伯特变换函数的频域和空域表达。
|
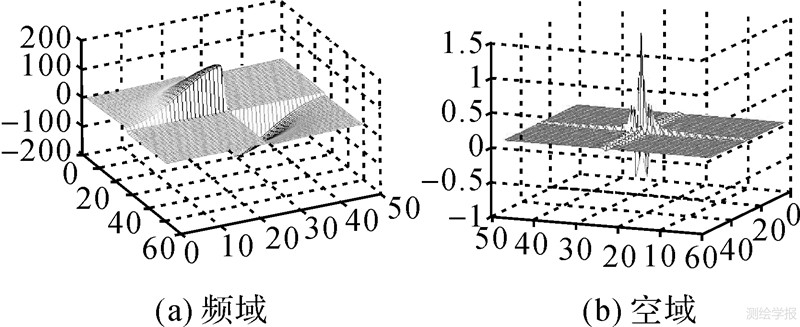
| 图 4 引入高斯函数的二维离散希尔伯特变换函数的频域和空域表达形式 Fig. 4 The description of 2-D discrete Hilbert transform with Gaussian function in frequency domain and spatial domain |
以图 1(a)给出的一维信号加噪后为例，来说明引入高斯低通滤波器后的希尔伯特变换方法在边缘特征检测过程中对噪声抑制的效果。
图 5中，将图 1(a)中的一维信号加入随机噪声得图 5(a)中信号。在此基础上，直接由希尔伯特变换得来的图像边缘检测结果(图 5(b))噪声过多。而经高斯滤波后，可以获得更好的信号边缘特征检测结果(图 5(c))。由此可知，加入高斯核函数的希尔伯特变换可以得到更好的检测结果。
|
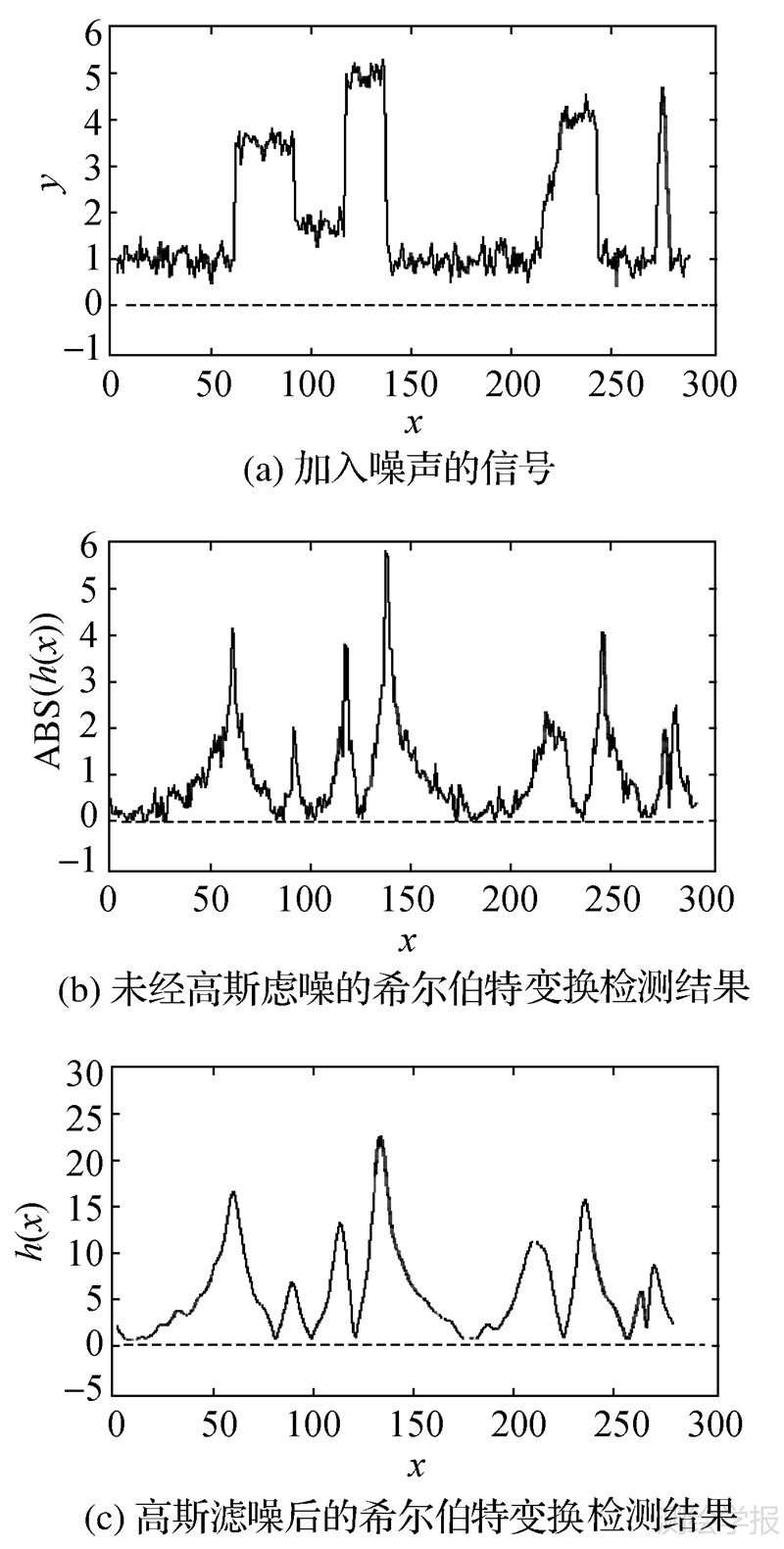
| 图 5 高斯滤波后的希尔伯特变换 Fig. 5 The result of Hilbert transform after filtering with Gaussian function |
因为高斯函数被用来抑制图像的噪声，所以参数σ的取值大小对边缘检测结果有直接的影响。本文利用PSNR(峰值信噪比)来确定最佳的参数σ。
式中，图像的灰阶为0~255；M和N分别为图像的行列数；F(i,j)为未加噪声时的边缘检测结果；I(i,j)为加噪声后，不同参数σ下的边缘检测结果。
图 6(a)为加入信噪比为18的高斯白噪声后的图像；图 6(b)为未加噪声时的边缘检测结果。利用本文所提方法，图 6(c)和(d)分别为σ取0.09和0.3时的边缘检测结果。可以明显看出σ=0.09时的边缘检测效果也高于σ=0.3。
|
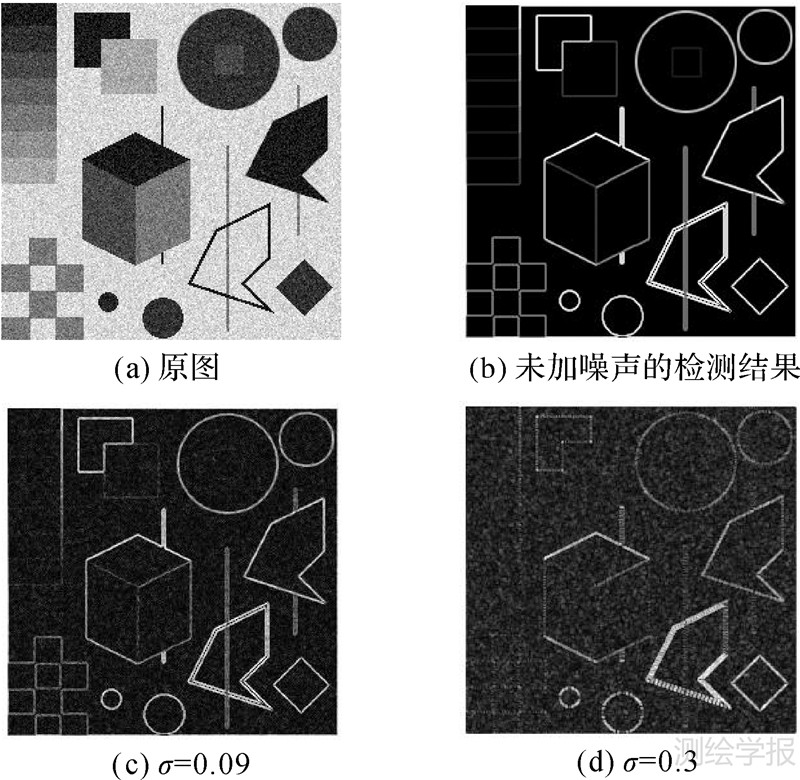
| 图 6 不同σ值下的边缘检测结果 Fig. 6 The edge detection with different σ |
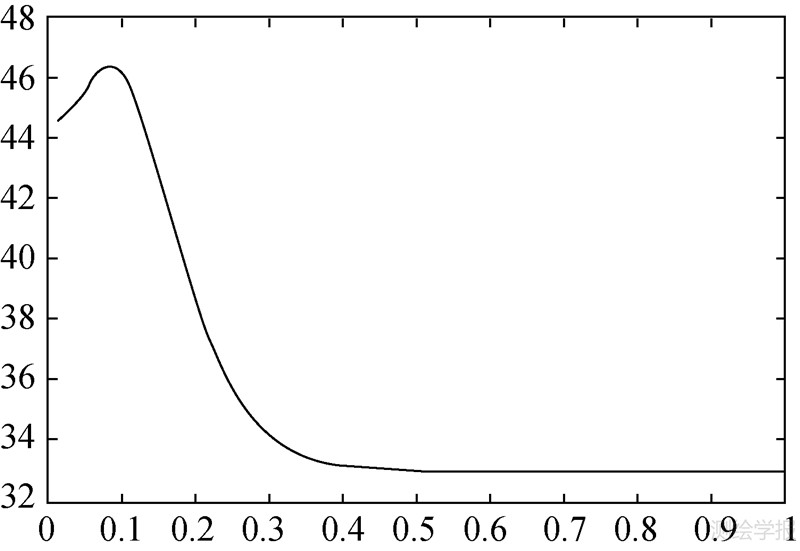
根据式(16)，计算不同参数σ下边缘检测结果的峰值信噪比(如图 7所示)。
|
| 图 7 不同σ值下的边缘检测结果的峰值信噪比 Fig. 7 The PNSR of edge detection with different σ |
从图 7可以看出，方差σ的取值区间为(0,1)时，PSNR随着σ的增大而先上升随后下降。最大值出现在σ=0.09处。即当σ=0.09时，可以得到最好的边缘检测效果(图 6(c))。
图 7说明，当σ增大时，滤噪效果更明显，因此边缘检测结果也更好；但是σ越大，其原图像中的边缘特征也会随之变得模糊，从而使得边缘变得模糊，尤其是线型的边缘特征甚至会消失。图 6(d)为σ=0.3时的检测结果，左下角的边缘特征已经变得非常模糊。
为了说明边缘检测结果的定位精度，则将图 6(c)中所示的边缘幅度图通过选定阈值以及细化操作得到单像素的边缘图像。然后利用F测度[24](式(17))来验证其边缘检测结果的定位精度。
式中，P和R计算公式如下
这里定义当检测边缘(S1)和标准参考图(S2)中边缘距离小于等于两个像素值时两边缘匹配。取α=0.5，最终F测度值结果为0.9695。边缘提取结果较理想，满足要求。
4 图像边缘检测结果评价及分析以下本文选取美国加州大学伯克利分校图像分割数据库(BSDS)中的图像为试验图像进行边缘检测，并与Canny 和Sobel算子的边缘检测结果进行评价分析。评价方法仍是通过PSNR值来实现。
图 8(a)为试验图像，图 8(b)为本文所提方法的边缘检测结果，其窗口大小为3像素×3像素，而方差σ=0.15。原图像左部的树枝的左右两侧与背景的灰度差异程度不同，导致其边缘检测响应的不同(右侧边缘检测响应值高于左侧边缘)。图 8(b)中，除了树枝和鸟的轮廓被很好地检测出来，爪子和枝芽等细节也有明显的检测效果。
|
| 图 8 BSDS图像及本文所提方法、Canny算子和Sobel算子的边缘检测结果 Fig. 8 Images in BSDS and edge features detection from the proposed algorithm, the algorithm of Canny and Sobel |
从图 8中可以看出，这几个方法的最终检测结果均达到了较为理想的视觉效果，Canny算子的检测结果中边缘信息宽度更大，但边缘响应值相对较大；而Sobel算子响应值相对较暗；本文方法的检测结果在边缘更加尖锐的同时，边缘响应值也较Sobel算子高。为了从定量的角度对边缘检测结果进一步分析，利用检测结果与标准参考图计算峰值信噪比来对本文所提方法进行比较评价。
从表 1可知，本文方法的PSNR高于Canny和Sobel算子，因此表明本文所提方法可有效应用于边缘检测工作中。
| 方法 | 本文方法 | Canny算子 | Sobel算子 |
| PSNR | 41.554 9 | 34.810 4 | 38.390 5 |
以上所用数据为自然图像，为验证该方法的适用广泛性，选取IKONOS卫星遥感图像(图 9)进行边缘检测试验。图 9(a)中主要地物有农田、池塘、建筑物、道路等，而图 9(b)则包括了道路、桥梁、河道、建筑物以及部分绿地。遥感图像中地物类型多，且不同地物类型间灰度差异较小，如图 9(a)中道路与邻近的绿地以及农田间的灰度差异不大。
|
| 图 9 IKONOS 图像 Fig. 9 IKONOS images |
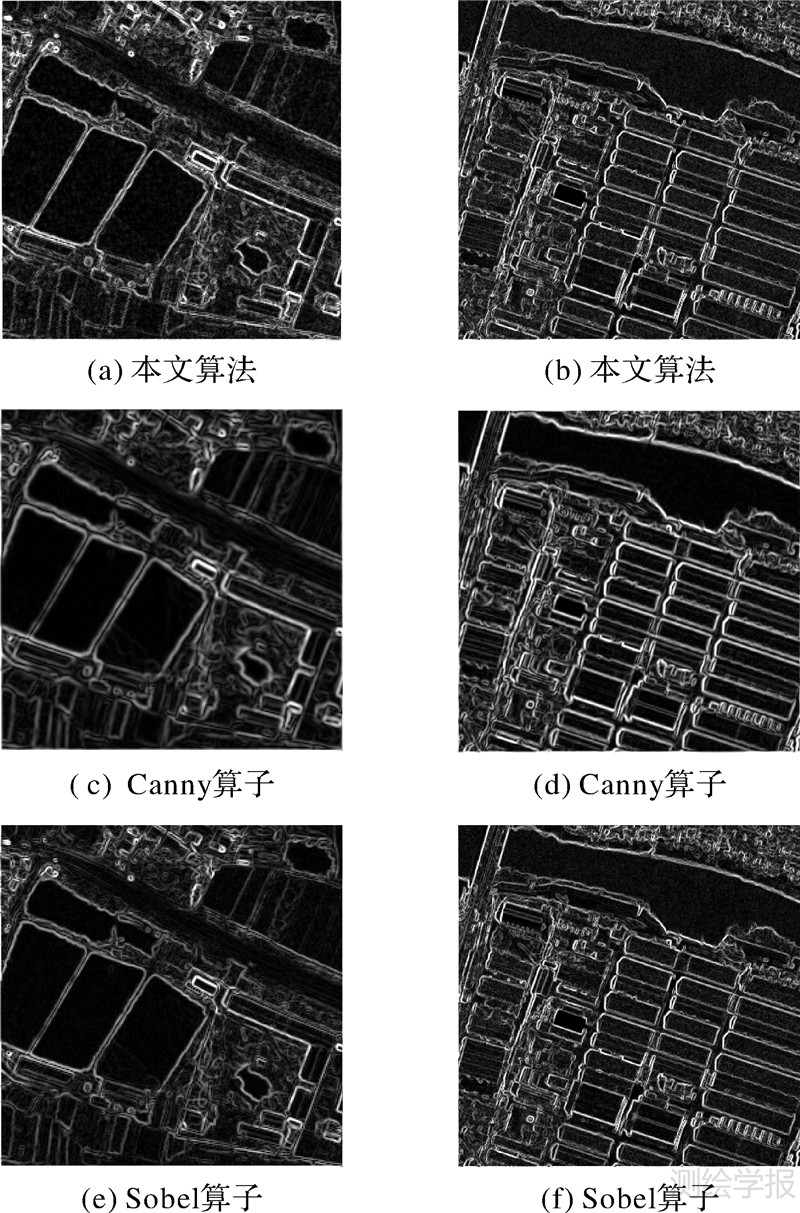
图 10(a)和10(b)给出了本文方法的检测结果，其中σ设置为0.1。图 10(a)中的水塘、建筑物边缘特征响应明显，农田内部的纹理也得到了很好的检测，而道路边缘由于与其周围地物间的灰度差异不大，造成边缘响应不够明显。图 10(a)和10(b)中主要的地物如河道、桥梁及建筑物边缘特征均被很好地检测。由于左侧建筑物比较细碎，且灰度差异偏小，所以其检测结果没有右侧建筑物边缘特征明显。
|
| 图 10 IKONOS 图像特征检测结果 Fig. 10 Features detection on IKONOS images |
图 10(c)、(d)、(e)和(f)分别为Canny和Sobel方法边缘检测结果。本文仍然利用峰值信噪比来对本文所提方法对遥感图像边缘检测结果进行比较评价(表 2)。峰值信噪比结果表明，本文所提的方法在遥感图像中的边缘检测结果优于Canny和Sobel算子。
| IKONOS图像 | 本文方法 | Canny算子 | Sobel算子 |
| 图9(a) | 63.621 4 | 32.835 2 | 38.786 4 |
| 图9(b) | 55.066 5 | 24.308 5 | 30.468 6 |
从BSDS的数据和遥感图像的检测结果可知，本文提出的引入高斯滤波的二维希尔伯特变换的检测方法可以很好地完成图像边缘特征检测。其检测效果的优劣取决于高斯函数中σ的值以及二维希尔伯特变换的卷积窗口。
5 结 论本文从希尔伯特变换对一维信号的边缘特征的明显表征出发，提出基于二维离散希尔伯特变换的边缘检测改进方法。首先针对二维离散希尔伯特变换的方向性特点，利用两个互呈90°分布的二维希尔伯特变换分别进行边缘检测，并将两者之和作为最终边缘检测结果。其次将高斯核函数引入到二维希尔伯特变换器中，从而获得具有除噪效果的边缘特征检测算子。同时为了获得最优边缘检测效果，提出利用PSNR来确定算子中的参数σ，并利用F测度对最优参数下的边缘检测结果进行了评价。最后，本文以BSDS图像数据和高分辨率遥感图像作为验证数据，对比分析了所提算法与Canny和Sobel算子的边缘检测结果，证明本文所提出的方法可有效地应用于图像边缘检测工作中。
| [1] | ROBERTS L G. Machine Perception of Three Dimensional Solids[C]//Optical and Electro-optical Information Processing. Cambridge: Massachusetts Institute of Technology Press, 1965:159-197. |
| [2] | SOBEL I. Neighborhood Coding of Binary Images for Fast Contour Following and General Array Binary Processing [J]. Computer Graphics and Image Processing, 1978, 8:127-135. |
| [3] | CANNY J F. A Computational Approach to Edge Detection [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(6):679-698. |
| [4] | MORRONE M C, OWENS R A. Feature Detection from Local Energy [J]. Pattern Recognition Letters, 1987, 6 (5):303-313. |
| [5] | FIELD D J. Relations between the Statistics of Natural Images and the Response Properties of Cortical Cells [J]. Journal of the Optical Society of America A, 1987, 4(12): 2379-2394. |
| [6] | KOVESI P. Invariant Measures of Image Features from Phase Information [D]. Perth: The University of Western Australia, 1996. |
| [7] | KOVESI P. Image Features from Phase Congruency [J]. A Journal of Computer Vision Research, 1999, 1(3): 1-26. |
| [8] | DUCOTTET C, FOURNEL T, BARAT C. Scale-adaptive Detection and Local Characterization of Edges Based on Wavelet Transform [J]. Signal Processing,2004, 84 (11): 2115-2137. |
| [9] | YI S, LABATE D, EASLEY D, et al. A Shearlet Approach to Edge Analysis and Detection [J]. IEEE Transactions on Image Processing, 2009, 18(5): 929-941. |
| [10] | TOIVANEN P J, ANSAMAKI J, PARKKINEN J P S, et al. Edge Detection in Multispectral Images Using the Self-organizing Map[J]. Pattern Recognition Letters, 2003, 24 (16): 2987-2994. |
| [11] | SHEN J, CASTAN S. An Optimal Linear Operator for Edge Detection[J]. CVGIP: Graphical Models and Image Processing, 1992,54(2):112-133. |
| [12] | BUSTINCE H, BARRENECHEA E, PAGOLA M, et al. Interval-valued Fuzzy Sets Constructed from Matrices: Application to Edge Detection [J]. Fuzzy Sets and Systems, 2009, 160 (13): 1819-1840. |
| [13] | XIAO Pengfeng, FENG Xuezhi, ZHAO Shuhe, et al. Segmentation of High-resolution Remotely Sensed Imagery Based on Phase Congruency [J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 146-152. (肖鹏峰, 冯学智, 赵书河, 等. 基于相位一致的高分辨率遥感图像分割方法[J]. 测绘学报, 2007, 36(2): 146 - 152.) |
| [14] | ZHAO Xi’an, LI Deren. Constructing Two Dimension Symmetric Wavelets for Extracting Edge Features of Image at Multiscales[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 113 - 119. (赵西安,李德仁. 2维对称小波与多尺度影像边缘特征提取[J].测绘学报,2003,32(4):113-119.) |
| [15] | KARANDE K J, TALBAR S N. Independent Component Analysis of Edge Information for Face Recognition [J]. International Journal of Image Processing, 2009,3(3):120-130. |
| [16] | RAMAMURTHY B, CHANDRAN K R. Content Based Image Retrieval for Medical Image Using Canny Edge Detection Algorithm [J]. International Journal of Computer Applications, 2011, 17(6):32-37. |
| [17] | LIVADAS G M, CONSTANTINIDES A G. Image Edge Detection and Segmentation Based on the Hilbert Transform [C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. New York: IEEE Computer Society, 1988: 1152-1155. |
| [18] | CHEN Xuehua, HE Zhenhua, HUANG Deji. Seismic Data Edge Detection Based on Higher-order Pseudo Hilbert Transform[J]. Progress in Geophysics, 2008, 23(4):1106-1110.(陈学华, 贺振华, 黄德济. 地震资料的高阶伪希尔伯特变换边缘检[J]. 地球物理学进展, 2008, 23(4):1106-1110.) |
| [19] | CHEN Xuehua, HE Zhenhua, HUANG Deji. High-order Pseudo Hilbert Transform and Application in Edge Detection [J]. Journal of Data Acquisition and Processing,2008,23(2):224-227.(陈学华, 贺振华, 黄德济. 高阶伪希尔伯特变换在边缘检测中的应用[J].数据采集与处理, 2008, 23(2):224-227.) |
| [20] | KOHLMANN K. Corner Detection in Natural Images Based on the 2-D Hilbert Transform [J]. Signal Processing, 1996, 48:225-234. |
| [21] | READ R R, TREITEL S. The Stabilization of Two-dimensional Recursive Filters via the Discrete Hilbert Transform [J]. IEEE Transactions on Geoscience Electronics, 1973, 11:153-160. |
| [22] | BOSE N K, PRABHU K A. Two-dimensional Discrete Hilbert Transforms and Computational Complexity Aspects in Its Implementation [J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1979, 27(4):356-360. |
| [23] | MARR D, HILDRETH E C. Theory of Edge Detection [C]//Proceedings of the Royal Society of London: Series B, Biological Sciences. London: the Royal Society, 1980:187-217. |
| [24] | Van RIJSBERGEN C J. Information Retrieval[M]. 2nd ed. London: Butterworths, 1979. |