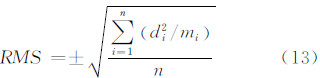2. 同济大学 空间信息科学及可持续发展应用中心，上海 200092
2. Center for Spatial Information Science and Sustainable Development, Tongji University，Shanghai 200092, China
1 引 言
GLONASS预计将在2011年年底达到满星座运行状态。GPS/GLONASS组合定位，可以成倍地提高卫星可用数量，改善卫星几何分布，提高卫星导航定位的可用性、可靠性、精确性及系统的自主完备性，弥补单一系统在某些情况下无法定位的缺陷。因此，GPS/GLONASS组合定位具有重要的应用前景。
GPS采用码分多址(CDMA)的方式调制卫星信号，所有卫星的频率相同；而GLONASS采用频分多址(FDMA)的方式调制卫星信号，不同卫星的频率不同，因此，所有涉及两颗GLONSS卫星观测值组合的问题都要比GPS复杂。例如，GLONASS双差观测值模糊度不能直接采用已有的GPS双差处理方法进行解算。在以周为单位的GLONASS双差观测方程中，无法消除接收机钟相对偏差的影响；在以距离为单位的双差观测方程中，不能构成GPS那样的双差模糊度。第1种情况可以先根据伪距单差求出接收机相对钟差，然后再固定双差模糊度[1,2,3]，但对伪距精度要求较高，一般的伪距测量精度无法满足要求。第2种情况将GLONASS双差观测方程的模糊度分解成参考卫星的单差模糊度和双差模糊度，先根据伪距求出参考卫星的单差模糊度，然后进行基线解算[4,5,6]，但是如果参考卫星的单差模糊度解算结果不准确，会引入一个系统性偏差。文献[7]提出先根据参考卫星的单差模糊度来固定双差模糊度，再根据固定后的双差模糊求参考卫星单差模糊度的整数解[8]，然后进行基线解算，这样计算显得非常繁琐，也增加了计算工作量。组合定位时，由于涉及两种类型的观测值，需要合理确定二者的权比[9,10,11,12,13]。
本文将GLONASS参考卫星的单差模糊度按实参数，双差模糊度按整参数进行估计，并将方差分量估计用于确定GPS和GLONASS观测值的权比，通过算例对GPS/GLONASS组合静态相对定位的结果进行分析。
2 时间与坐标系统的统一GPS采用GPST，以UTC(USNO)为时间度量基准，GLONASS采用GLONASST，以UTC(SU)为时间度量基准。GPST与UTC相差为整数跳秒，GLONASST与UTC相差3h，需要进行时间的转换。但在实测的GLONASS星历文件(G文件)中，采用的时间系统并非GLONASST，而是UTC，故在与GPS组合定位的数据处理中，两者之间只相差一个整数跳秒[14]。
GPS采用WGS-84坐标系，GLONASS采用PZ-90坐标系，在数据处理时要进行坐标系统的转换。据文献[15]介绍，GLONASS坐标系统于2007年由PZ-90更新到PZ90.02，与ITRF差异保持在分米量级，PZ90.02与ITRF2000的差异只有原点平移，在X、Y、Z方向分别为：-36 cm、+8 cm、+18 cm。而WGS-84与ITRF2000差异很小，其误差可以忽略。因此，本文只考虑PZ90.02与WGS-84之间的平移参数。
3 GPS/GLONASS组合静态相位相对定位模型假设参考站r、流动站u在某一历元同时对GPS卫星i、m和GLONASS卫星j、n进行观测，卫星i和j是参考卫星，则可得GPS、GLONASS的载波相位双差观测方程分别为
以距离为单位，式(1)与式(2)可表示为 式中，Δ表示单差算子；∇Δ表示双差算子；Φ为载波相位观测值；ρ为卫地距离；N是载波相位模糊度；λ为载波波长；f为卫星频率；δt为接收机钟差。
由上式可知，载波相位双差观测方程消除了卫星钟差，减弱了卫星星历误差、对流层和电离层延迟误差的影响。GPS的双差观测值也消除了接收机钟差的影响，而GLONASS的双差观测方程，由于不同卫星采用不同的频率，接收机钟差无法消除，其双差模糊度不具有整周特性，因此GLONASS双差观测值的模糊度处理要比GPS复杂得多。
需要说明的是，在上式中，GPS和GLONASS各选了一颗参考卫星，组成的是单系统双差。实际上，也可以选择一颗GPS或GLONASS卫星作为参考卫星，组成双系统双差，双系统卫星双差较单系统卫星双差多形成一个观测方程，更加充分地利用观测值。但系统间差分时，如果系统间系统误差处理不好，反而会降低定位结果的精度[16]。因此，组合定位通常采用系统内差分，提高定位精度。
对定位结果的精度评定采用如下方法进行计算，单位权中误差估值为
式中，V为观测值的残差；P为权矩阵；t为未知参数个数；n为观测值总数。
基线向量中任一分量的精度估值为
式中，Qxx为未知数x的协因数元素。 4 GPS/GLONASS组合静态相位相对定位关键问题 4.1 GPS/GLONASS模糊度解算
对于GPS卫星，站星双差可以消除接收机钟差，且双差模糊度保持整数特性。 GPS模糊度解算采用文献[17,18]提出的LAMBDA(least-square ambiguity decorrelation adjustment)方法。
对于GLONASS卫星以周为单位的观测方程式(2)，由于残余钟差的影响，破坏了双差模糊度的整数特性。如果利用伪距计算残余钟差，要使钟差误差引起的GLONASS双差模糊度的误差小于0.1周，则对应于7.31 MHz的最大载波频率差，残余钟差的精度要求达到1.37×10-8 s，一般GLONASS接收机无法满足这一要求。
以距离为单位的双差观测方程式(4)，尽管没有接收机残余钟差项，但不同GLONASS卫星的频率不一样，不能形成类似于GPS的双差模糊度，需要对式(4)的模糊度项变换如下[4,5,6,7,8]
式中，Δλnj=λn－λj，则式(4)可表示为
这样，将原来的两个单差模糊度变换成一个双差模糊度和一个与参考卫星有关的单差模糊度。由式(8)可见，单差模糊度项
的影响与两颗卫星的波长Δλnj之差有关，若要求bnj的误差不影响双差模糊度
的解算，其误差对双差模糊度的影响应小于0.1周(对应误差为2 cm)，则不同卫星组合对单差模糊度的最大误差要求如表 1所示(采用2005年之后的频段)。
| 卫星组合 | 相对于参考卫星 的波长之差/m | 单差模糊度最大 允许误差/周 |
| GLONASS-GLONASS(min) | 0.000 066 | 303 |
| GLONASS-GLONASS(max) | 0.000 85 | 23 |
| GPS-GLONASS(max) | 0.003 55 | 5 |
由表 1可知，当对波长之差最大的两颗GLONASS卫星求双差时，单差模糊度的最大允许误差为23周，若根据伪距和相位的关系用下式进行计算
考虑到其他误差的影响，假设P码的精度为1 m，载波相位的精度为0.1周，而GLONASS的最小波长为18.67 cm，根据误差传播定律公式
可得到单差模糊度的精度约为8周，多个历元的单差模糊度取平均，可进一步提高精度，完全能满足固定双差模糊度的要求。而且，单差模糊度只需按实参数估计，而双差模糊度必须按整数进行求解。
4.2 GPS/GLONASS的方差分量估计GPS/GLONASS组合定位时，由于涉及两个系统的观测值，需要合理确定两者的权。文献[19]用单历元观测值进行方差分量估计定权，但是单历元多余观测数太少，因此其估值不可靠。本文根据 GPS/GLONASS一个时段的所有观测数据进行方差分量估计，确定两类观测值之间的权比[9]。
确定不同类观测值的权通常采用方差分量估计。常用的方法有Helmert估计法、最小范数二次无偏估计法(MINQUE)等，理论上，当不同类观测值不相关时，这两种方法是等价的。本文采用Helmert估计法估计两类观测值之间的权比。
GPS、GLONASS的Helmert方差分量估计过程如下[20]：
(1) 第一次最小二乘平差时，根据经验给GPS、GLONASS观测值先验定权P1、P2。
(2) 进行最小二乘平差，求得
。
(3) 按下式进行方差分量估计
式中，
；n1为GPS观测值的个数；n2为GLONASS观测值的个数；N1、N2分别为GPS与GLONASS的法方程系数阵，N=N1+N2。
(4) 按下式重新定权
式中， c 为任意常数，一般取
中的某一个值。
(5) 反复进行步骤(2)～(4)，直到
为止，或通过必要的检验认为各类单位权方差之比等于1为止。在本文中，迭代终止的条件为
，其中
为绝对值算子。
以某工程GPS控制网为例，共37条基线，组成24个最小独立闭合环，基线边长207 m～2189 m，基线观测时间均大于60 min，观测数据类型有C1、P1、P2、L1和L2。
采用以下3种方案进行基线解算，并计算最小独立环闭合差和基线精度，分别用来评定3种方案的外符合精度和内符合精度。
方案1：GPS静态相对定位。
方案2：GLONASS静态相对定位。
方案3：GPS/GLONASS方差分量估计静态相对定位。
图 1为3种方案的24个最小独立环3个方向的闭合差。其中，图 1(a)～(c)分别为X、Y、Z方向的环闭合差。由图 1知，从环闭合差结果来看，GLONASS短基线解算的外符合精度在毫米级水平，和GPS解算结果处于同一量级，但精度和稳定性均低于GPS。采用Helmert方差分量估计定权解算时，求得GLONASS与GPS观测值的权比在0.323 3~1.785 9之间，基线的外符合精度与GPS相当，这是因为GPS卫星数量较多，GLONASS卫星数量较少，加入GLONASS对外符合精度的提高有限。
|
| 图 1 24个最小独立环3个方向的闭合差 Fig. 1 Misclosure of 24 independent loops |
根据n个闭合环各个方向的环闭合差di(i=1,2,…,n)，按公式(13)计算3个方向环闭合差的均方根误差RMS。
式中，mi为第i个闭合环的基线数。RMS计算结果如表 2所示，由表 2可知，GPS/GLONASS组合定位的RMS较GPS和GLONASS都要小，这也说明了组合定位的外符合精度较单一GPS系统有所提高，但提高得并不明显，较单一GLONASS系统有较大提高。
| 方案 | RMS | ||
| X | Y | Z | |
| 1 | 0.310 0 | 0.565 5 | 0.320 2 |
| 2 | 0.885 5 | 1.649 7 | 0.899 5 |
| 3 | 0.272 9 | 0.521 5 | 0.314 5 |
图 2为根据式(6)计算的3种方案的基线精度。其中图 2(a)～(c)分别为X、Y、Z方向的精度估值。由图 2可知，GLONASS短基线解算结果任一方向的内符合精度能达到毫米级，但是一般比GPS精度要低，采用Helmert方差分量估计定权时基线精度较单一GPS或GLONASS有较大提高，提高幅度最大超过50%。由此可见，加入GLONASS后，可以显著提高定位结果的内符合精度。
|
| 图 2 37条基线3个方向的基线精度 Fig. 2 Precision of 37 baselines |
对其中的一条基线边进行单历元解算，用GPS/GLONASS整体方差分量估计得到的权作为GPS和GLONASS观测值之间的权比进行联合解算，同时采用单系统GPS进行单历元解算。图 3为两种方法单历元解算的基线与整体解算基线3个方向偏差(ΔXi,ΔYi,ΔZi)平方和的平方根，根据式(14)进行计算。
|
| 图 3 单历元解算基线偏差 Fig. 3 Baseline bias of single epoch solution |
图 4为两种方法单历元解算的基线精度比较，图 5为单历元的PDOP值比较。由图 3、4、5可知，采用GPS/GLONASS组合静态相对定位可以显著改善可见卫星几何强度，降低PDOP值。和单一GPS系统相比，单历元解算的基线精度和可靠性都有明显提高，稳定性也大大增强。
|
| 图 4 单历元解算基线精度 Fig. 4 Baseline precision of single epoch solution |
|
| 图 5 单历元PDOP值 Fig. 5 PDOP of single epoch |
根据图 3单历元解算的基线偏差Δi，按公式(15)计算两种方案的RMS。
其结果如表 3所示，GPS/GLONASS组合定位单历元解算基线偏差的RMS较单一GPS小，基线精度约提高了10%。
在城市、山区等某些特殊地区，受高楼或其他障碍物的遮挡，有时单一GPS系统的可用卫星数难以达到4颗，导致定位的精度和可靠性均比较低，甚至出现不能定位的情况。为了展示GPS/GLONASS组合定位的优越性，从观测文件中选取3颗GPS卫星和3颗GLONASS卫星，观测时间为30 min，采样间隔15 s，共120个历元，对21条基线进行解算。其解算结果与采用所有卫星解算结果的偏差如图 6所示，其统计结果见表 4。由此可见，当GPS卫星数较少且观测时间较短时，GPS/GLONASS组合基线解算的精度明显高于单一GPS系统，表明了在遮挡比较严重的情况下，GPS/GLONASS组合定位具有明显的优势。
|
| 图 6 GPS、GPS/GLONASS解算3个方向基线偏差 Fig. 6 Baseline bias of 3 directions |
当同步观测3颗GPS卫星和3颗GLONASS卫星时，单一GPS或GLONASS系统已经无法进行单历元基线解算，但利用GPS/GLONASS组合观测值仍可进行联合解算。图 7为3颗GPS卫星和3颗GLONASS卫星组合单历元解算基线与采用所有卫星解算基线3个方向偏差平方和的平方根，其根据式(14)进行计算。由图 7可知，即使在GPS可用卫星数较少时，GPS/GLONASS组合基线解算在大部分情况下仍能达到厘米级精度。
|
| 图 7 3颗GPS+3颗GLONASS卫星单历元解算基线偏差 Fig. 7 Baseline bias of single epoch solution with 3 GPS+3 GLONASS satellites |
将GLONASS参考卫星的单差模糊度按实参数求解是合理的，可以得到精度较高的定位结果；GPS/GLONASS组合定位时，采用Helmert方差分量估计确定两类观测值的权比，其组合静态相对定位较单一系统解算的基线精度均有提高，尤其比GLONASS有显著提高，比GPS也有一定提高，其中单历元解的基线精度提高达到10%；当单一GPS或GLONASS系统可用卫星数较少时，GPS/GLONASS组合定位更能体现出优势。
| [1] | LEICK A.Aspects of GLONASS Carrier-phase Differencing[J].GPS Solutions,1998,2(1):36-41. |
| [2] | HAN S,DAI L, RIZOS C.A New Data Processing Strategy for Combined GPS/GLONASS Carrier Phase-based Positioning[C]//Proceedings of the ION GPS-99.Nashville:[s.n.],1999:1619-1628. |
| [3] | HU Guorong,CUI Weihong.Combined GPS/GLONASS Precise Positioning for Long-distance Baselines[J].Geo-spatial Information Science,2001,4(1):24-27. |
| [4] | WANG J.An Approach to GLONASS Ambiguity Resolution[J].Journal of Geodesy, 2000, 74:421-430. |
| [5] | ZHANG Yongjun,XU Shaoquan,WANG Zemin,et al.Ambiguity Processing Approach in Combined GPS/GLONASS Positioning[J].Geomatics and Information Science of Wuhan University,2001,26(1):58-63.(张永军,徐绍铨,王泽民,等.GPS/GLONASS组合定位中模糊度的处理[J].武汉大学学报:信息科学版,2001,26(1):58-63.) |
| [6] | GAO Xingwei,LI Yulin,GE Maorong.Data Processing of GPS/GLONASS Carrier-phase Difference[J].Science of Surveying and Mapping,2004,29(2):22-24.(高星伟,李毓麟,葛茂荣.GPS/GLONASS相位差分的数据处理方法[J].测绘科学,2004,29(2):22-24.) |
| [7] | HABRICH H.Geodetic Applications of the Global Navigation Satellite System(GLONASS) and of GLONASS/GPS Combinations[D].Switzerland:University of Berne,1999. |
| [8] | WANG J,RIZOS C,STEWART M,et al.GPS and GLONASS Integration:Modeling and Ambiguity Resolution Issues[J].GPS Solutions,2001,5(1):55-64. |
| [9] | DUAN Juju,SHEN Yunzhong.GPS/GLONASS Combined Point Positioning Using Variance Component Estimation[J].Bulletin of Surveying and Mapping,2011(4):4-6.(段举举,沈云中.基于方差分量估计的GPS/GLONASS组合点定位[J].测绘通报,2011(4):4-6.) |
| [10] | YANG Yuanxi,GAO Weiguang.Integrated Navigation by Using Variance Component Estimates of Multi-sensor Measurements and Adaptive Weights of Dynamic Model Information[J].Acta Geodaetica et Cartographica Sinica,2004,33(1):22-26. (杨元喜,高为广.基于方差分量估计的自适应融合导航[J].测绘学报,2004,33(1):22-26.) |
| [11] | YANG Yuanxi,ZENG Anmin.Fusion Modes of Various Geodetic Observations and Their Analysis[J].Geomatics and Information Science of Wuhan University,2008,33(8):771-774.(杨元喜,曾安敏.大地测量数据融合模式及其分析[J].武汉大学学报:信息科学版,2008,33(8):771-774.) |
| [12] | WANG Guangding,ZHANG Shengkang,YANG Ruliang.User Position Computation Based on Passive Beidou and GLONASS Navigation System Combination[J].Acta Geodaetica et Cartographica Sinica,2007,36(4):377-382.(王光鼎,张升康,杨汝良.基于北斗无源与 GLONASS导航系统的卫星组合导航用户位置计算[J].测绘学报,2007,36(4):377-382.) |
| [13] | YANG Yuanxi.Adaptive Kinematic Navigation and Positioning[M].Beijing:Publishing House of Surveying and Mapping,2006.(杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006.) |
| [14] | SUN Hongrui,SHEN Yunzhong,ZHOU Zebo.Integrated GPS/GLONASS Point Positioning Model and Its Accuracy Analysis[J].Engineering of Surveying and Mapping,2009,18(1):8-10.(孙洪瑞,沈云中,周泽波.GPS/GLONASS点定位模型及其精度分析[J].测绘工程,2009,18(1):8-10.) |
| [15] | ENGELSBERG V,BABAKOV V,PETROVSKI I.GLONASS Business Prospects[J].GPS World,2008,19(3):12-15. |
| [16] | PRATT M, BURKE B, MISRA P.Single-epoch Integer Ambiguity Resolution with GPS-GLONASS L1-L2 Data[C]//Proceedings of the ION GPS-98.Nashville:[s.n.],1998:389-398. |
| [17] | TEUNISSEN P.The Least-squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation[J].Journal of Geodesy,1995,70:65-82. |
| [18] | TEUNISSEN P.The Least-squares Ambiguity Decorrelation Adjustment:Its Performance on Short GPS Baselines and Short Observation Spans[J].Journal of Geodesy,1997,71:589-602. |
| [19] | HU Guorong,CUI Weihong.Method of Weighted GPS/GLONASS Single Point Positioning[J].Acta Armamentarii,2002,23(1):59-63.(胡国荣,崔伟宏.组合GPS/GLONASS加权单点定位方法[J].兵工学报,2002,23(1):59-63.) |
| [20] | CUI Xizhang,YU Zongchou,TAO Benzao,et al.Generalized Surveying Adjustment [M].Wuhan:Press of Wuhan University,2005.(崔希璋,於宗俦,陶本藻,等.广义测量平差 [M].武汉:武汉大学出版社,2005.) |