2. 武汉大学 测绘遥感国家重点实验室,湖北 武汉430079
2. State key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
1 引 言
城市是GIS的运用与研究领域的一个重要方面,三维城市模型是许多应用领域迫切需要的,已被广泛运用于城市规划、建筑设计、无线通信等领域[1, 2]。在诸多城市地物中,立交桥作为一种由主体桥面、空间交叉以及空间连接部分等多种构造物组成的多层三维地物,是城市交通网络的重要部分,也是城市道路中最复杂的环节[3]。而城市立交桥的可视化已成为数字化城市建设的重要课题。
在已有城市地物建模的研究中,地理实体的可视化表达包括以下手段:3DFDS拓扑空间数据模型[4],基于4面体的三维数据模型[5],基于表面剖分的3DCM空间数据模型[6],SSM简化空间模型[7, 8]。这些数据模型试图用通用的方式来表达所有地理空间实体,并没有考虑立交桥自身的几何特点以及实体之间的空间关系。除此之外,一些学者通过将影像与DSM叠加构造城市地区的景观模型[9],但是将立交桥当做地形表面上的构造物同样无法体现其空间关系。文献[10]提出利用规则的几何体基元(如长方体,圆柱体,椎体)进行地物重建,然而其作用仅限于表达城市建筑物、格网状道路等规则地物,无法适用于立交桥等不规则地物。一些商业化软件针对立交桥有单独的表示,有代表性的如Arc/Info软件将立交作为点来处理,通过对该点的一系列相关数据的设置来表达立交桥的属性。这种通过数据来描述立交的方式在相关数据处理时比较方便,但缺乏形象性且数据结构复杂,无法提供用户直观的感受以及相关的交互式的处理。目前为止,对于城市大型立交桥的可视化建模只能依靠人工方式在CAD环境下手动建立三维模型,而这样将耗费大量的人力资源,制作周期较长。因此,高效、自动化的立交桥可视化建模一直以来是三维城市建模中难以解决的问题。
机载激光雷达系统作为一种新型的对地观测传感器近十几年来取得飞速的发展和广泛的应用。LiDAR系统能够直接获取地物表面的高精度、高密度的三维点云,同时提供激光脚点的回波次数以及强度信息,除此之外,多数设备还能够提供全波形数据(如Leica,Toposys等)。这其中,高精度的表面点云数据为空间地物的三维可视化建模提供了可靠条件[11, 12]。许多研究成果基于此进行城市地物的提取与三维建模[13, 14, 15, 16],取得了不错的效果。这也推动了利用LiDAR数据进行立交桥可视化建模的进一步研究。
笔者提出一种基于机载LiDAR点云数据的城市大型立交桥建模的方法与流程,建立完整的立交桥可视化模型。
2 方 法 2.1 立交桥脚点提取立交桥建模的基础工作是将立交桥脚点从LiDAR点云中分离出来。立交桥具有特殊的几何特征,多层次的空间结构,主要部分位于地面之上,而引桥部分则与地面平缓相连,基于这种特殊结构,立交桥的提取需要有效的点云滤波算法(将非地面点与地面点分离)作为前提。文献[17]提出一种滤波算法,基于剖面点集分割的思想,以多角度扫描线的方式对点集进行分割,分割按照坡度阈值,在分割后的同一区域内点之间建立连接,由此形成多个独立连通区域。通过判断区域的特性实现地面点集与非地面点集的分离。该方法完整性较好,且对于多个层次、不同地物形状具有抗差性,适用于立交桥地物,但算法在局部区域由于判断标准单一造成错误分割的情况。针对这个问题,笔者对文献[17]的算法进行改进。不同于单一的阈值划分,利用局部平面约束对剖面点集进行分割,将处于不同平面的点集分离,然后将坡度变化平缓的相邻点集进行合并,由此实现更为精细的分割。结合非地面点的判断准则,能够避免错误分割的出现,进一步提升了算法的效果。
完成滤波后的非地面点集由多个城市地物的数据点集所组成,同一地物的数据点相互聚集,不同地物之间形成多个具有一定距离的子集,这其中包含有立交桥形成的子集。将滤波后所有的非地面点集作为立交桥种子点,首先求取点集中每一个子集的精确轮廓。城市立交桥由于其跨越了较长距离,与城区中的其他地物相比,立交桥的尺寸应大于一般的城市建筑物以及人造地物。通过筛选多个子集形成的轮廓集合中含有最大长度线段的轮廓,由此准确的锁定立交桥位置,轮廓内的点即是立交桥点。
其中轮廓求取采用Alpha-Shape算法[19, 20]。该算法的优势在于可以重建无序点集的边缘形状。其原理可以比作一个半径为alpha的圆在点集外部滚动,如果存在空洞与间隙大于alpha值,还可以滚动到点集内部,将其分割为多个独立子集,滚动的轨迹既是各个子集的精确边缘[21],这刚好能满足种子点区域分割和轮廓筛选的要求。
2.2 基于轮廓分析的立交桥区段自动分割立交桥含有多个交汇与分叉的结构,不同区段在路面宽度以及高程上均有较大差别。对于此种结构,统一的建模方法可能难以进行,而且数据采集中由于多层次结构遮挡的而缺失的部分也难以恢复。
如果将边缘平行、路面宽度稳定的较短区域作为单一区段,立交桥结构可以看做是多个不同高程、宽度的单一区段的交汇与分叉组合。基于以上特点,提出分割后建模的策略,提出基于轮廓分析的自动分割方法将立交桥整体分割成结构简单的单一区段后单独建模。这样既能保证立交桥整体和局部的几何特征,又为后续建模等算法处理提供基础和前提。
区段分割方法基于区域增长过程中的点集轮廓分析,分两种情况对立交桥中的分叉和交汇结构进行检测,从而进行分割。其思想如下,将轮廓中连续的边的集合称为段,在区域增长中,轮廓由不同类型的段所组成,其中包括增长开始的起始段。除此之外,一种称为S段(static段),意为在两次以及两次以上区域增长的迭代过程中保持位置不变的轮廓边的集合。另一种为G段(growing段),是轮廓中除去起始段以及S段后剩下的部分,在每一次迭代过程中位置不断变换,如图 1。在区域增长迭代的过程中可以发现,对于路面宽度保持稳定,迭代过程处于某个简单结构的路段内时,点集轮廓中S段末尾的长度会不断增加,而G段的长度保持稳定。当遇到分叉或交汇结构时,轮廓的组成和不同段的状态就会发生变化,如图 2、图 3所示,由此作为检测的依据。这里还需要定义一种DS段(duo-static段)。DS段与S段特征相同,但在迭代过程中轮廓中DS段的两端长度都会增长。在分割算法中存在一些回滚(rollback)操作,需要在完成检测后回溯到之前的某个状态。
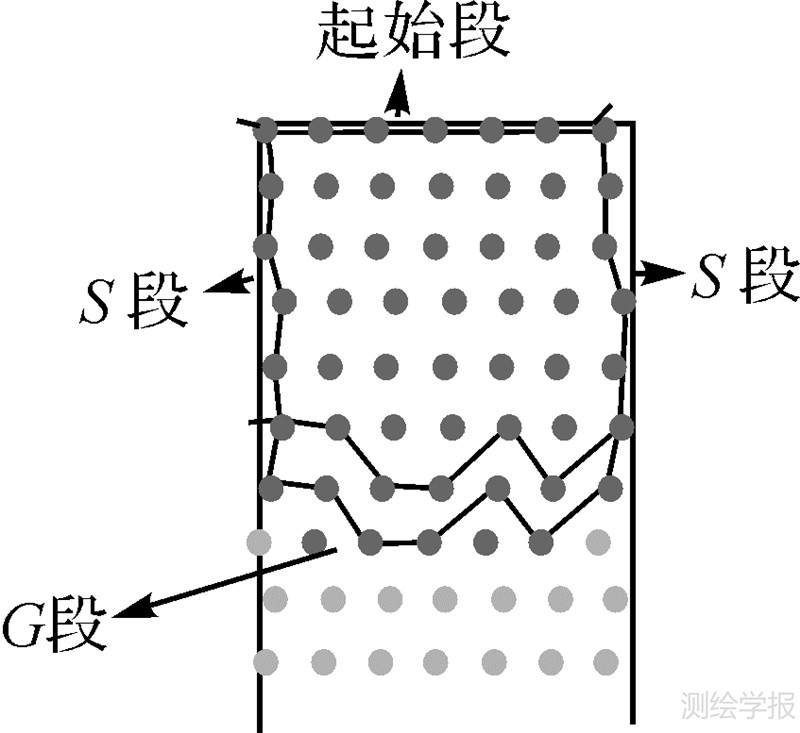
|
| 图 1 轮廓分析 Fig. 1 The contour analysis |

|
| 图 2 分叉结构检测 Fig. 2 The bifurcate structure detection |

|
| 图 3 交汇结构检测 Fig. 3 The joint detection |
具体步骤如下:
(1) 选取立交桥上桥处的边缘点区域增长的起始点集P,其连成的边为起始段,标记为区段i。
(2) 利用Alpha-shape算法计算区段i的轮廓(算法初始时的轮廓就为起始段本身)。对于轮廓上的每一点,以该点为中心取半径为R的邻域,计算轮廓范围之外落入邻域内的数据点,选择距离该点最近的点作为新增长的点纳入到点集P中。若该点已被轮廓上的相邻点选中,则计算除去该点之外的最近点,由此直到轮廓上所有点的新增长点选取完毕,更新点集P并重新计算区段i轮廓。
(3) 计算步骤2前后S段的长度,并检测轮廓中的段落成分与状态。若轮廓中S段长度变长且在G段中检测出DS段,将区域增长算法回滚到区段的轮廓中第一次含有属于该DS段的数据点时的状态,将第一次包含的DS段中的数据点标记为D点(图 2(b))。结束该区段点集的增长,将G段划分为D点到两个S段的末结点之间的两段,分别作为区域i+1,i+2的起始段进行区域增长(图 2(c))。
(4) 若在区域增长轮廓中,有一端的S段长度变短且在G段中检测出DS段,如图 3(b)。记录D点,回滚到该S段达到最长长度时的状态。结束区段i的增长,取D点与该S段的末节点,计算两点间直线的两侧距离最近的点集g。由D点与该S段末节点作为起点和终点与g组成的边为起始段1,标记新区段i+1,以起始段1加上轮廓中两个S段末节点之间的段落作为起始段2,标记区段i+2,分别进行区域增长,如图 3(c)。由于这种情况下的两个区域的起始段有部分重合,故在选择增长点时需要加入方向判断(数据点在左侧或者右侧),避免错误方向的区域增长。
(5) 重复步骤2~步骤4直到所有区段划分完毕。
2.3 全约束三角网建模将不同区段的点集分割后,分别对单一区段进行建模。本文采用文献[22]提出的全约束三网算法(all-constraint triangulation algorithm)。该算法不同于离散点的三角网内插算法,将区域两侧的边作为约束边建立三角网,适用于道路以及桥面等窄条区域的模拟。同时,三角网算法本身可以有效地保留地物的空间特征。
分割后的区段i轮廓的组成包括区段i的起始段、起始段两端的两条S段以及末尾的区域j的起始段,如图 4(a)。全约束三角网建模算法的应用,应将首尾起始段用直线代替,两条S段作为约束边,由此进行建模。但由于边缘处点云分布不规则,轮廓中有多处段落呈锯齿状,在此基础上建模的效果难以令人满意。因此建模之前必须对区段轮廓进行处理,使得轮廓具有光滑的、规则的边缘。本文采用一种折线的弯曲简化(line bend-simply)算法[23]。其特点在于可以保留轮廓中相邻两段之间具有角度变化较大的关键点保留轮廓的几何形态,同时删除冗余的节点,能够保证简化后轮廓中各种成分段落的首末端点位置不变,如图 4(b)。简化后,将轮廓中的起始段用直线代替,完成轮廓处理。建模算法将轮廓中的S段作为约束边,具体步骤如下:

|
| 图 4 轮廓简化及全约束三角网 Fig. 4 Simplified contour and All-constraint triangulation network |
(1) 对于每一个区域i,确立两条约束段,也就是轮廓简化后两条用直线代替的起始段之间的两条S段。
(2) 分别选择两条约束段的起点a、b,a、b之间的连线即为轮廓处理后用直线代替的起始段,在此作为搜索边AB。
(3) 利用构成的三角形中最小角最大原则,选择与点a或b邻近的一点。如果是ABP为锐角三角形,构成三角形ABP。如果ABP为钝角三角形,选择离搜索边AB最近的一点S,构成三角形ABS。
(4) 当新的三角形ABP或ABS构成,点P或S与a或b的连线作为新的搜索边AB,如图 4(c),重复步骤3。
(5) 当区域i中的所有点都已构成三角网,结束建模。
2.4 遮挡结构恢复多层次的立交桥由于上层的遮挡在数据采集时会造成下层数据的缺失,无法获得直接测量的结果。在工程应用中,一些商业化公司选择将机载LiDAR与车载设备结合应用,这样的做法以互补的方式解决了此类问题,但是多种平台设备的联合使用以及数据之间的配准会使工程成本增加。本文将不同区段进行三角网建模后,根据先验知识,如果在立交桥中连贯的路段由于上层结构的遮挡在数据中的某一段存在缺失,那么这一路段形成的两个不同区域在路面宽度以及坡度变化上应该保持一致或连续,由此利用三角网信息检测就可以判断出被遮挡的结构和走向。这其中可以选取的特征包括区段的AB边的平均长度、区段末尾处的切线方向,末尾处三角形的法向量以及高程等。本文方法选择对区段末尾三角形的特征进行判断,具体步骤如下:选定两个不同区域,定义距离阈值与高程、法向量角度的容差,若两个区域的末尾三角形Ti、Tj的中心之间距离小于阈值且Ti、Tj高程与法向量角度之差在容差范围内。则认为该处存在被遮挡的结构,利用三角网将两个区段末尾连接,如图 5虚线部分。至此立交桥的完整路面结构已经完成了可视化建模。

|
| 图 5 遮挡恢复 Fig. 5 Occluded structure restoration |
为检验文章算法的合理性和可行性,利用在Windows XP环境下,Visual C++语言自主研发的平台ALDpro作试验,试验数据采集于2009年的广西南宁城市建筑物密集地区。数据采集时飞行高度为1300 m,航带宽约1500 m,最大扫描角60°。地区中含有大型立交桥,如图 6。数据范围900 m×1200 m,数据大小39.2 MB,包含激光点146万,航向点间距约为0.9 m,旁向点间距约为1.1 m,平均点云密度约为1.2点/m2。

|
| 图 6 点云数据 Fig. 6 The laser point cloud data |
图 7为立交桥提取过程以及结果,其中图 7(a)为Alpha-shape提取的种子点轮廓,图 7(b)为轮廓筛选后提取的立交桥脚点。与人工分类结果相比,本文提取算法的精度达到了93%以上。

|
| 图 7 立交桥提取 Fig. 7 Cloverleaf points extraction |
图 8为区段分割过程,其中图 8(b)中不同的颜色代表分割后的不同区段,同时展示了区段分割时的区域增长轨迹,每一步区域增长后利用Alpha-shape算法求取点集的精确轮廓。从图 8(c)中的区段轮廓可以看出,本文算法成功的将立交桥的复杂结构分割成结构简单的单一区段,从而为建模工作打下基础。

|
| 图 8 区段分割 Fig. 8 The segmentation process |
图 9代表轮廓简化处理后的轮廓,以获得较为光滑、规则的边缘。需要注意的是,某些区段由于处于立交桥范围边缘或被遮挡结构的两端,其在结尾处并未存在其他区域的起始段,而是轮廓中的两条S段在末尾处相连,此时需要在轮廓简化算法执行后在较为规则的轮廓中检测两条S段的末尾处线段之间角度变化较大的节点。将两个节点之间用直线代替,并将两条S段作为约束边进行建模,由此完成轮廓处理。图 9(b)为全约束三角网建模,三角网携带高程信息,有助于重建立交桥的三维结构。图 9(c)为面渲染显示俯视图,图 9(d)为侧视图,图 9(e)为点云与模型的叠加显示,可以看出在空间位置和几何尺寸上模型与原始数据是完全吻合的。

|
| 图 9 立交桥建模过程 Fig. 9 Cloverleaf modeling |
图 10显示了本文方法重建的遮挡结构,如图 10(a),圆圈1、2处。在参数设置上,遮挡判断的三角形Ti、Tj之间的距离阈值等于 ×最大路面宽度,在本试验中为55.2 m,高程容差设置为0.3 m,法向量角度容差为5°。试验结果显示,在点云数据缺失的地方,本文方法能够成功检测并恢复该处的结构,恢复的结构与被遮挡的路段特征保持一致,使得立交桥模型在三维可视化表达上更加完整。
×最大路面宽度,在本试验中为55.2 m,高程容差设置为0.3 m,法向量角度容差为5°。试验结果显示,在点云数据缺失的地方,本文方法能够成功检测并恢复该处的结构,恢复的结构与被遮挡的路段特征保持一致,使得立交桥模型在三维可视化表达上更加完整。

|
| 图 10 遮挡结构恢复 Fig. 10 Restoration of occluded structure |
作为建模质量的评价,将立交桥模型的主桥、支路中心线的长度以及路面宽度与高分辨率正射影像上(由高分辨率DMC影像制作,地面分辨率0.3 m)的人工量测结果进行比较,结果显示中心线长度差别在0.50 m以内,路面宽度差别在0.11 m以内。笔者还将立交桥环形匝道中心线上的采样点与影像上同名点曲率进行比较,曲率半径的差别在0.03 m以内。在算法效率上,提取算法在100万点以上数据耗时约110 min,在提取立交桥脚点后,自动区段分割算法耗时约50 min,建模以及遮挡结构恢复耗时约20 min。整个流程在3 h左右。由此看出,本文算法在建模质量以及运行效率上是可行的、有效的。
4 结 论不同于传统的统一建模方法以及一些系统中对于立交桥的抽象数据表示,本文方法结合立交桥自身的结构特点,建模算法中进行了有针对性的处理,并取得了良好的效果。主要特点包括:① 采用了分割后建模的策略,对立交桥整体进行分割,将多个分叉、交汇的复杂结构分割成路面宽度一致,路段两侧边缘平行的单一结构;② 建模算法采用全约束三角网算法,适用于分割后的区段;③ 能够利用区段的模型信息恢复立交桥下层被遮挡的结构,重建立交桥完整的三维结构。从整体流程与试验结果可以看出,自动化建模的算法流程是可行的。建立的立交桥可视化模型与原始数据在地理位置与范围上保持一致,在关键的几何参数上保证在误差范围内。不仅可以用于三维城市模型、数字城市的建设上,在城市交通设计,交通设施管理与交通状况监测上发挥重要作用。有待提高的是,本文的遮挡检测算法是基于模型信息和立交桥的先验知识,而非直接量测的结果,在遮挡严重以及含有不规则遮挡结构的情况使用有限,需要地面观测数据的补充以及采用更为高效的算法,笔者在后续的工作中会展开研究。可在保留模型地理信息的基础上对模型进行编辑和美化等方面的改进,如在模型中加入路面厚度等立面,添加边缘的扶手以及隔离带等,进一步增加立体感和真实感,更加符合城市景观的实际。
| [1] | YANG Bisheng, LI Qingquan, MEI Baoyan. Study of the Visualization of Three-dimension Urban Model[J]. Acta Geodaetica et Cartographica Sinica. 2000, 29(2): 149-154. (杨必胜,李清泉,梅宝燕.三维城市模型的可视化研究[J].测绘学报,2000, 29(2):149-154.) |
| [2] | CHEN Aijun, XU Guangyou, SHI Yuanchun. Automated 3D Building Modeling Based on Urban Aerial Stereopair[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(1):54-59. (陈爱军,徐光佑,史元春.基于城市航空立体像对的3维建筑物建模[J].测绘学报, 2002, 31(1): 54-59.) |
| [3] | SHAO Zhenfeng, LI Deren, CHENG Qimin, et al. An Intergrated Method for 3D Reconstruction of the Interchange[J]. Journal of Geomatics, 2003, 28(4):1-3. (邵振锋,李德仁,程起敏,等.立交桥三维建模的集成方法研究[J].测绘信息与工程, 2003, 28(4): 1-3.) |
| [4] | MOLENAAR M. A Formal Data Structure for 3D Vector Maps[C]//Proceedings of EGIS’90: 2. Amsterdam: [s.n.], 1990: 770-781. |
| [5] | PILOUK M. Integrated Modeling for 3D GIS[D]. Amsterdam: ITC,1996. |
| [6] | SUN Min, CHEN Jun. A 3DCM Data Model Based on Surface Partition[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3): 257-265. (孙敏,陈军.基于表面剖分的3DCM空间数据模型研究[J].测绘学报, 2000, 29(3):257-265.) |
| [7] | ZLATANOVA S, RAHMAN A, PILOUK M. 3D GIS: Current Status and Perspectives[C]//Proceedings of the Joint Conference on Geo-spatial Theory, Processing and Applications. Ottawa: [s.n.], 2002. |
| [8] | ZLATANOVA S, RAHMAN A, SHI W Z. Topological Models and Frameworks for 3D Spatial Objects[J]. Computers and Geosciences, 2004, 30(4): 419-428. |
| [9] | HAALA N, BRENNER C, ANDERS H K. Generation of 3D City Models from Digital Surface Models and 2D GIS[C]//International Archives of Photogrammetry and Remote Sensing: 32(3-4W2): 3D Reconstruction and Modeling of Topographic Objects. Stuttgart: ISPRS, 1997: 68-75. |
| [10] | RANZINGER M, GLEIXNER G. GIS Datasets for 3D Urban Planning[J]. Computer Environment and Urban Systems, 1997, 21(2):159-173. |
| [11] | WEHR A, LOHR U. Airborne Laser Scanning: An Introduction and Overview[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2-3): 68-82. |
| [12] | AXELSSON P. Processing of Laser Scanner Data—Algorithms and Applications[J]. ISPRS Journal of Photogrammetry and Remote Sensing. 1999, 54(2-3): 138-147. |
| [13] | MASAHARU H, HASEGAWA H. Three-dimensional City Modeling from Laser Scanner Data by Extracting Building Polygons Using Region Segmentation Method[C]//International Archives of Photogrammetry and Remote Sensing: 33(B). Amsterdam: ISPRS, 2000: 556-562. |
| [14] | VOSSELMAN G. 3D Reconstruction of Roads and Trees for City Modelling[C]//International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences: 34. [S.l.]: ISPRS, 2003: 231-236. |
| [15] | BRENNER C. Building Reconstruction from Images and Laser Scanning[J]. International Journal of Applied Earth Observation and Geoinformation, 2005, 6(3-4):187-198. |
| [16] | CLODE S, ROTTENSTEINER F, KOOTSOOKOS P, et al. Detection and Vectorization of Roads from LiDAR Data[J]. Photogrammetric Engineering and Remote Sensing, 2007, 73(5): 517-535. |
| [17] | SITHOLE G, VOSSELMAN G. Experimental Comparison of Filter Algorithms for Bare-earth Extraction from Airborne Laser Scanning Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1-2): 85-101. |
| [18] | SITHOLE G, VOSSELMAN G. Filtering of Airborne Laser Scanner Data Based on Segmented Point Clouds[C]//Proceedings of the ISPRS Workshop Laser Scanning 2005. Enschede: ISPRS, 2005. |
| [19] | EDELSBRUNNER H, MUCKE E P. Three-dimensional Alpha Shapes[J]. ACM Transactions on Graphics, 1994, 13(1): 43-72. |
| [20] | BERNARDINI F, BAJAJ C. Sampling and Reconstructing Manifolds Using Alpha-shapes[R]. West Lafayette: Purdue University, 1997: 1-12. |
| [21] | SHEN Wei, LI Jing, CHEN Yunhao, et al. Algorithms Study of Building Boundary Extraction and Normalization Based on LiDAR Data[J]. Journal of Remote Sensing, 2008, 12(5): 692-698. (沈蔚,李京,陈云浩,等.基于LiDAR数据的建筑物轮廓线提取及规则化算法研究[J].遥感学报, 2008, 12(5): 692-698.) |
| [22] | SUN M, CHEN J. A 3-dimensional Data Model for Visualizing Cloverleaf Junction in a City Model[C]//Proceedings of International Workshop on Urban 3D/Multi-media Mapping. Tokyo: [s.n.], 1999: 203-208. |
| [23] | WANG Z S, MULLER J C. Line Generalization Based on Analysis of Shape Characteristics[J]. Cartography and Geographic Information Systems,1998, 25(1) :3-15. |


