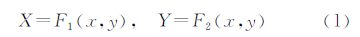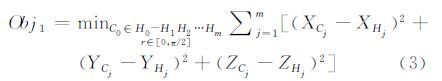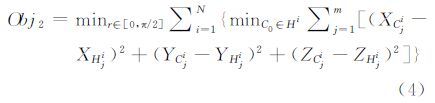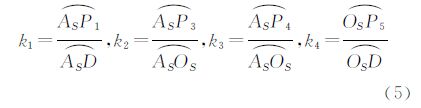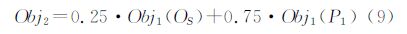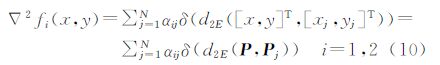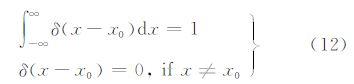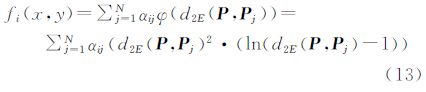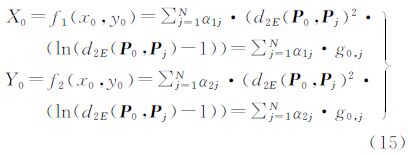2. 北京师范大学 地表过程与资源生态国家重点实验室,北京100875
2. State Key Laboratory of Earth Surface Processes and Resource Ecology,Beijing Normal University, Beijing 100875, China
1 引 言
全球离散格网系统(discrete global grid system,DGGS)是用特定方法将地球均匀离散化,形成无缝无叠的多分辨率格网层次结构,并采用格网单元的地址编码代替传统地理坐标参与数据操作的一种新型全球空间数据结构[1, 2]。其中,采用理想多面体代替球面构建格网的方式被许多学者所采用[3, 4, 5, 6, 7],并在诸多领域得到了应用[8, 9, 10]。基于理想多面体的离散格网系统由多面体的选择、多面体的定位、多面体面上的层次剖分、平面与球面的对应和点在格网单元中的分布5个要素唯一确定[1, 11]。其中,多面体表面与球面的对应关系是格网从平面到球面的关键步骤,值得深入研究。
平面与球面的对应通常采用直接法和投影法实现。相比较而言,直接法比较直观,各种几何指标在剖分的过程中可以明确地进行约束,但由于球面剖分的复杂性,较难得到任意层次理想的剖分方法;而投影法具有相对较高的效率和灵活性,因而被更多研究者所采用[1, 4, 6, 11]。本文选择全球六边形格网作为研究目标,主要是因为六边形的覆盖效率和角度分辨率均比三角形、四边形高[4, 10, 11, 12],单元不仅一致相邻,而且无共顶点的角邻近单元,这些特性使得六边形格网非常适合用作空间数据的处理。在构建全球六边形离散格网系统的研究中,最著名的是采用文献[13]提出的“Snyder等积多面体投影”(Snyder equal-area polyhedral projection)。该投影虽然能够严格保证格网的等积特性,但其他相关几何特性存在一些问题,导致边、角的变形较大,另外,Snyder等积多面体投影采用了浮点运算和迭代运算,导致运算效率较低,难以保证高效的数据转换的应用需求。
本文以全球六边形格网为研究对象,采用直接法和投影法相结合的方式,利用数值投影变换理论,建立平面与球面的对应关系,为构建几何属性更优的球面离散格网系统打下基础。该思路同样也可扩展到其他类似的球面格网上,例如三角形格网、四边形格网等。
2 方法与步骤 2.1 基本思路根据地图投影变换理论,投影过程可以狭义地理解为建立两个平面场之间点的一一对应的函数关系[14]。设一平面场点位坐标为(x,y),另一个平面场的坐标为(X,Y),则地图投影变换方程式为
数值变换法是在原投影的坐标解析式不知道,或者不易求出两投影点之间坐标的直接联系的情况下,采用多项式逼近的方法来建立两投影间的变换关系式。相对而言,采用数值投影变换方法,数学表达式较简单,利用线形或非线性的多项式逼近投影方程,多项式的系数在计算投影变换的过程中被预先算好,因此投影转换的效率相对要高,并且可以根据目标投影对指标变形的要求,给出满足变形指标的控制点,只要控制点的密度和数目足够,可以得到满足精度要求的投影方程。关于数值投影变换的精度问题,文献[14]给出了详尽的讨论。
本文以文献[1, 12, 15]中基于二十面体,孔径为4的六边形层次剖分方法4HI为例,设计了一种新的球面格网与平面格网的转换方案,下面给出基本思路:
(1) 利用球面直接剖分方法在球面二十面体三角面上进行初始层次格网的剖分,在剖分的过程中保证每一层剖分单元满足特定的统计指标以保证格网的均匀性。由于球面问题的复杂性,格网的逐级剖分不可能到无限层,这样只能在有限的格网层次上,剖分出尽可能满足要求的球面单元,这些单元的边界点和中心点可以准确地得到球面坐标;
(2) 按照文献[1]的方法,在平面三角面上,按照4HI结构剖分出对应层次的六边形单元,计算单元中心与边界的平面坐标;
(3) 将平面与球面上对应单元节点的坐标作为两个场之间的控制数据,利用数值投影变换理论计算两种坐标场之间的转换关系。当同名控制点数据能足够密集且分布合理,能保证数据的转换精度时,可以利用这种关系将任意层次的平面六边形格网转换到球面上。理论上,采用数值投影变换的方法可以逼近任意两种平面场,同样也可以用来逼近例如Snyder投影等,在保证精度的情况下进一步提高效率。
2.2 数值投影变换的坐标系设置数值投影变换需要的是位于两类场上的控制点,以二十面体展开面的其中一个三角面为研究对象,三角面是一个平面场,其上的控制点可以用图 1(a)中的以三角面中心为原点建立的标准笛卡尔坐标系坐标来记录。平面三角面转换到球面上对应的是球面三角形区域,并不满足数值投影变换要求的平面场,但实际上平面场的概念并不完全要求区域是平面,只要求该区域能够用相互独立的二维变量表达的区域都可以认为是平面场。从文献[14]所提供的试验来看,在使用数值投影变换过程中,两类坐标系统越具备相似性,则为满足相同精度而需要的同名点的数目越少。根据这样的思路,在球面三角面上构造类似的坐标系统,将常见的球面直角系统[16]作进一步修改,使得它与三角面上的笛卡儿坐标系更加类似(图 1(b))。

|
| 图 1 平面直角坐标系与球面直角坐标系的对应关系 Fig. 1 The correspondence between the orthogonal coordinates on plane and the orthogonal coordinates on spherical surfaces |
(1) 确定球面二十面体顶点在球面上的定位[1];
(2) 对于任意球面△ASBSCS,其中S=1,2,…,20,取其球面中点OS,过OS与AS作球面大弧 =π/2,将
=π/2,将 作为球面直角坐标系的YS轴;
作为球面直角坐标系的YS轴;
(3) 根据右手法则,过OS点作大弧 =π/2,使得∠MSOSNS=π/2,将
=π/2,使得∠MSOSNS=π/2,将 作为球面直角坐标系的XS轴,建立球面直角坐标系OS-XSYS;对于球面三角面上的任意一点PS,过MS和PS作大弧
作为球面直角坐标系的XS轴,建立球面直角坐标系OS-XSYS;对于球面三角面上的任意一点PS,过MS和PS作大弧 的垂直圈
的垂直圈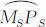 ∩
∩ ,过NS和PS作大弧
,过NS和PS作大弧 的垂直圈
的垂直圈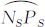 ∩
∩ ,令
,令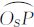 SX=xP、
SX=xP、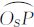 SY=yP,则球面点PS的球面直角坐标为(xS,yS)。
SY=yP,则球面点PS的球面直角坐标为(xS,yS)。
设球面三角面的3个角点的经纬度坐标分别为:AS(λA,φA)、BS(λB,φB)、CS(λC,φC),为计算方便,令球体的中心为SO,其半径R=1,建立空间直角坐标系SO-XYZ,其中SOZ指向球面的真实北极;SOX指向0度经线与赤道的交点;SOY的指向遵循右手法则,则球面三角形的中点OS经纬度坐标有
则λO=arctan(YO/XO),φO=arcsin ZO。可以利用空间直角坐标和球面三角的方法计算球面三角面上的任意点PS(λP,φP)转换到球面直角坐标系的坐标值PS(xP,yP),方法略。
2.3 球面格网几何最优化评价指标文献[1, 17]在评价不同格网性质的过程中使用了一系列几何指标,包括:单元面积变化率VS、单元角度变化率VA、单元边长变化率VC等。从这些指标中可以发现,采用解析投影法生成的离散格网,无论哪一种都不可能在所有指标中都取得最好的效果,部分指标之间甚至是矛盾的。这实际上也给球面上直接的格网剖分带来了巨大的困难,毕竟如果多个目标存在,势必导致规划目标的不明确,带来剖分的盲目性。
分析球面的情况,格网越均衡,每个单元的变形就越小,越接近一个理想的球面正多边形。理想球面正多边形,满足边界点Ci,i∈{1,2,…,m}落在以中心CO为极点,球面半径为r的球面伪纬圈(一系列相互平行的平面与球面的交线称为伪纬圈[18])上,并且∠C1C0C2=∠C2C0C3=…=∠Cm-1C0Cm=∠CmC0C1=π/m。
每一个球面格网单元与理想球面多边形单元相似程度越大,则球面格网本身就越均匀。对于球面离散格网中任意一个格网单元H0-H1H2…Hm而言,必然存在理想单元中心CO∈该实际格网单元H0-H1H2…Hm与球面半径r,用(XW,YW,ZW),W∈{H0,H1,…,Hm,C0,C1,…,Cm}表示球面点的空间直角坐标,利用欧氏距离定义两个格网间的相似性程度,必然存在式(3)的情况。当Obj1=0时,该实际单元就是理想的球面正多边形,Obj1数值的大小显示了与理想单元之间的差异。
同样对于整个球面格网系统,如果格网单元为N,要求每一个球面实际单元Hi与球面理想单元Ci都尽可能相似(i=1,2,…,N),并且还要求实际格网单元之间尽可能均衡,这就要求与每一个实际单元最相似的理想单元的球面半径r尽可能相等,还需要保证实际单元与理想单元之间的差异最小。这样不但能保证单元本身形状的规则性,还能保证单元之间的均衡性,式(4)给出了这样的指标
Obj2提供了描述最优球面格网的单目标规划,可以作为衡量球面格网系统几何属性优劣的唯一标准,取Obj2的最小值即可满足建立最优化离散格网的需求。
2.4 球面直接格网剖分的最优化方法为了建立球面与平面之间的关联,需要在球面上获得满足格网剖分要求的一系列控制点,采用直接法在球面上逐层剖分生成。剖分的过程中使用目标Obj2进行约束,以达到最优的剖分效果。由于球面离散格网是逐层剖分的,首先给出两个假设:
(1) 第n层的格网必然是在第n-1层格网的基础上继续剖分而成的,即前一层剖分生成的单元边界点或单元中心在下一层将被保留。
(2) 第n层的最优化格网应该是建立在第n-1层最优化格网基础上的最优化,这样每一层格网都是前一层基础上的最优化。
下面使用反证法说明这两个假设的合理性。如果不遵循这两个假设,对任意层次n的格网按照目标Obj2进行全局最优化的搜索剖分,先不说该全局最优化是否能得到最终的优化结果Gn,即使得到了,同样对于n-1层也可以得到类似的优化结果Gn-1,两次优化的结果是独立的最优化过程,将无法严格保证{Gn-1的单元中心和边界点}⊂{Gn-1的单元中心和边界点},这样相邻层单元间将不满足继承关系,这与设计层次格网的初衷是矛盾的,因此这两个假设是必须的也是合理的。
根据上面的优化思路,在格网剖分的过程中逐层优化,使得每一层的单元都满足式(4)的目标。考虑二十面体一个三角面的情况,根据对称性,其余三角面上的情况类似。在球面△ASBSCS,其中S=1,2,…,20,按照4HI的逐层剖分方式,从n=2的初始层次进行剖分,其余的层次n>2的直接剖分方法类似,不再赘述。为说明问题方便,图 2采用平面三角形的方式代替球面三角形。

|
| 图 2 球面三角形上,剖分层次n=2时的直接剖分情况 Fig. 2 The situation of direct subdivision on spherical triangle,and the partition layer n=2 |
由于球面三角形是对称图形,取大弧 、
、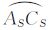 、
、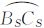 的中点D、E、F,OS是△ASBSCS的球面中心,有球面四边形ASDOSE
的中点D、E、F,OS是△ASBSCS的球面中心,有球面四边形ASDOSE BSFOSD
BSFOSD CSEOSF,因此只考虑其中一个球面四边形ASDOSE即可,如图 2(b)。在球面三角形上进行剖分,关键是找到几个控制点,对于图 2(b)的情况,要剖分出六边形单元需要获得8个控制点Pi,i=1,2,…,8的球面坐标,由这8个控制点和已知点构成4个球面六边形(或部分),OS-P5P4P6(1/3个单元)、P1-P7P3P4P5D(1/2个单元)、P2-P8P3P4P6E(1/2个单元)、AS-P7P3P8(1/5个单元)。需要注意的是,单元AS-P7P3P8在球面二十面体的展开面上是五边形的一部分[1],因此是1/5个单元。
CSEOSF,因此只考虑其中一个球面四边形ASDOSE即可,如图 2(b)。在球面三角形上进行剖分,关键是找到几个控制点,对于图 2(b)的情况,要剖分出六边形单元需要获得8个控制点Pi,i=1,2,…,8的球面坐标,由这8个控制点和已知点构成4个球面六边形(或部分),OS-P5P4P6(1/3个单元)、P1-P7P3P4P5D(1/2个单元)、P2-P8P3P4P6E(1/2个单元)、AS-P7P3P8(1/5个单元)。需要注意的是,单元AS-P7P3P8在球面二十面体的展开面上是五边形的一部分[1],因此是1/5个单元。
由于图 2(b)的球面四边形区域是关于轴 对称的,因此P1和P2、P5和P6、P7和P8是对称的,又因为二十面体每一个球面三角形都是对称的,有
对称的,因此P1和P2、P5和P6、P7和P8是对称的,又因为二十面体每一个球面三角形都是对称的,有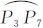 ⊥
⊥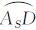 ,
,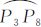 ⊥
⊥ 。根据对称性,需要求解的控制点实际上只有P1、P3、P4、P5 4个,剩下的P2和P6与P1和P5关于
。根据对称性,需要求解的控制点实际上只有P1、P3、P4、P5 4个,剩下的P2和P6与P1和P5关于 中心对称,P7和P8可以利用AS、P3和∠ASP7P3=∠ASP8P3=π/2在球面△ASP7P3和△ASP8P3中求解。因此,利用优化算法进行剖分时只需要确定4个参数即可。由于P1∈
中心对称,P7和P8可以利用AS、P3和∠ASP7P3=∠ASP8P3=π/2在球面△ASP7P3和△ASP8P3中求解。因此,利用优化算法进行剖分时只需要确定4个参数即可。由于P1∈ ,P3,P4∈
,P3,P4∈ ,P5∈
,P5∈ 给出下面4个参数
给出下面4个参数
其中,0≤ki≤1,i=1,2,3,4。根据这4个参数,即可利用已知点AS、D、OS、E的坐标计算8个控制点的坐标值。下面的问题是如何设置约束条件。
在图 3(b)中,利用坐标系旋转和参数ki可以得到控制点坐标,利用控制点间的球面距离可以得到球面单元的中心到边界点的弧长:L0=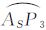 、L1=
、L1= 、L2=
、L2= 、L3=
、L3=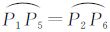 、L4=
、L4=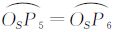 、L5=
、L5=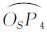 。对于式(4)的优化目标而言,先在每个球面六边形单元中搜索理想单元中心,再在所有单元中搜索球面半径,以满足Obj1和Obj2两个目标,运算量是巨大的,甚至是不可能完成的工作。根据球面剖分的实际情况,将Obj2目标的求取进行简化。
。对于式(4)的优化目标而言,先在每个球面六边形单元中搜索理想单元中心,再在所有单元中搜索球面半径,以满足Obj1和Obj2两个目标,运算量是巨大的,甚至是不可能完成的工作。根据球面剖分的实际情况,将Obj2目标的求取进行简化。

|
| 图 3 406对同名控制点(分别采用平面直角坐标和球面直角坐标)在一个坐标系中表示 Fig. 3 The spherical and planar orthogonal coordinates of 406 pairs homologous control points were expressed in the same coordinate system |
简单来说,可以用弧长的均值L=(∑i=05Li)/6来代替式(4)中的r,但实际上这仍是有缺陷的,因为每一个Li在n=2层的球面格网上出现的次数是不一样的,这就代表着每一个Li具有不同的权值。由于{Li∈面ASBSCS}∩{Li∈面AS′BS′CS′}=∅,则只需要考虑一个三角面中的情况即可。对于图 2(a)中的情况,Li的出现的次数分别为ω0=3、ω1=6、ω2=6、ω3=6、ω4=3、ω5=3,得到新的L=(∑i=05ωiLi)/∑i=0Nωi。
特殊情况是球面四边形AS-P7P3P8,它是五边形单元的一部分,如果也采用L作为理想五边形单元的球面半径,不但会导致它与采用L作为球面半径的理想六边形单元在面积、边长、角度等属性上相差较大,还会使得与它相邻的5个六边形单元发生较大形变,破坏了格网的均衡性。一种有效的修正办法就是将L0从求L加权的过程中去掉,由于对称性,五边形单元一定都是理想单元,必有Obj1=0,这里只是不将其与六边形单元进行比较,使得约束条件全面保障六边形单元的均衡。式(6)给出了计算L的方法,其中N=5。
在式(4)的最优化目标约束中,除了球面半径外,还有一个重要的就是要确定理想单元相对于球面实际单元的相互位置关系,以保证式(3)中的Obj1取得最小值。这里有两个问题需要解决:① 理想单元中心的定位;② 理想单元相对于实际球面单元之间的偏移。下面分别给出解决方案:
(1) 第1个问题,实际上从图 2(b)和式(5)中已经得到了答案,根据对称性,OS必然是球面单元的中心,P1和P2也同样是球面单元的中心,AS是五边形单元的中心,这4个单元中心可以根据已知点AS、D、OS、E的坐标和k1唯一确定。
(2) 第2个问题,就是理想单元相对于实际球面单元的偏移问题。由于理想单元是对称单元,在确定了中心点C0的情况下,只需要再确定一个方向就能确定两个单元的相对位置。同样,对于OS-P5P4P6单元,将C0与OS重合,C0C1与OSP4方向重合即可;将C0与P1(P2)重合,C5C6(C2C3)的方向与P4P3(P3P4)的方向重合即可;为保证六边形单元的均衡性,五边形单元不进行约束。
确定好单元之间的相互关系后,下一步就是确定实际单元与理想单元之间的差异。用dnE(a,b),n=1,2,3,…,m表示n维直角坐标系下点a、b间的欧氏距离。从图 2(b)中可以发现,没有一个单元是完整的单元,其中OS-P5P4P6是1/3个单元,根据对称性,有
P1-P7P3P4P5D(1/2个单元)和P2-P8P3P4P6E(1/2个单元)两者全等,有
不考虑五边形单元的约束Obj1(AS)。根据三角面的对称性及二十面体的重复性,在整个n=2层的球面格网上,Obj1(OS)出现20次,Obj1(P1)出现了60次,因此给Obj1(OS)设置权值为0.25,给Obj1(P1)设置权值为0.75,得到最终的目标Obj2为
对于任意一个参数组合(k1,k2,k3,k4)可以得到一个Obj2目标,n=2层的最优化格网即当时k1~k4∈[0,1],求取Obj2的最小值所对应的格网。在确定了优化目标之后,还需要明确的是优化方法。该问题是一个典型的非线性优化问题,目标Obj2与变量k1~k4之间的解析关系比较复杂,用传统的非线性函数的优化很难得到较好的优化结果,因此本文思考使用启发式的优化算法解决该问题,其中遗传算法就是一种性质优良的启发式优化算法。在试验中,我们采用遗传算法进行系统整体优化,对于n=2层的球面格网,二十面体一个三角面内可以获得28个控制点。
2.5 数值投影变换构建全球离散格网本文选择双谐波样条插值的方式进行球面直角坐标系与平面直角坐标系间的数值投影转换,最重要的原因是这种样条插值方式对控制点的间距没有要求,不像传统数值投影变化中采用的三次、二次等距样条插值那样,对控制点间的距离有明确要求[19],或者采用多项式分片插值的方式,对面与面接边处的光滑情况处理不好[20]。它可以对任意不规则的控制点进行整体内插,生成表面曲率最小的光滑曲面,并且运算效率相对较高,而采用类似图 2的控制点排布方式显然不是均匀的。
根据文献[19]的描述,引入二维双谐波样条插值。设平面三角面上控制点的直角坐标为(xj,yj),对应球面三角面上同名点的球面直角坐标为(Xj,Yj),其中j=1,2,…,N,令向量[x,y]T=P,则Pj=[xj,yj]T,这些点内插控制点使得用于样条的基函数Green函数加权后满足双谐波方程,其中,αij为基函数的权值。
其中,δ为脉冲函数,它满足定义
式(10)中4阶微分方程的通解为式(13),根据文献[19]中表 1对任意维双谐波的基函数Green函数的表述,当纬度为2时,Green函数φ(x)=|x|2(ln|x|-1),则
令d2E(Pk,Pj)2(ln(d2E(Pk,P1-1))=gk,j,则gj,j=0,式(13)写成离散形式有
用矩阵表示Fi=G·Ai,其中F1=[X1,X2,…,XN]T,F2=[Y1,Y2,…,YN]T,其中G为满秩方阵,则向量Ai=G-1·Fi,代入内插方程(13)中,得到二维双谐波样条插值的表达式。i=1,2时分别对应着对X和Y的差值,如式(11)。对于平面三角面中的点(x0,y0),采用式(15)得到球面三角面上的内插结果
3 试验与分析首先利用遗传优化进行球面的直接剖分。根据文献[1]中的二十面体上三角面的定位情况,其中某个球面三角形的3个顶点的经纬度坐标为A5(0°,90°)、B5(0°,26.565 05°)、C5(72°,26.565 05°)。设球体为单位球,则球面△A5B6C5的球面中心为O5(0.491 12,0.356 82,0.794 65)。利用遗传算法,计算n=2时的格网最优化剖分,试验中,采用二进制Gray码对k1~k4进行编码,为避免算法早熟,使用指数函数α1/Obj2(a=1.1)作为目标函数,其他参数种群N=600,杂交概率pc=0.7,变异概率pm=0.01,最大遗传代数M=600。得到参数优化的结果为:k1=0.643 63、k2=0.267 73、k3=0.628 93、k4=0.636 38。对应目标:Obj2=0.007 598 9,其中Obj1(OS)=0.029 636、Obj1(P1)=0.000 253 15。同样,利用优化的参数组合(k1,k2,k3,k4),可以得到图 2中第2层优化的球面控制点的空间直角坐标

将这些点的空间直角坐标和A5、B5、C5、O5的空间直角坐标当做已知参数,利用2.4节类似的方法,计算n=3时的格网最优化剖分,根据三角面的对称性和第3层优化获得的控制点,共得到球面三角面上82个控制点,共优化参数8个。同样的方式,对于剖分层次n=4的情况,可以得到对应406个同名控制点的球面直角坐标,共优化参数21个。图 3显示了406对同名控制点(分别采用平面直角坐标和球面直角坐标记录)在一个坐标系中的情况,采用文献[1]中第4章中的结论,对应平面三角形的边长取
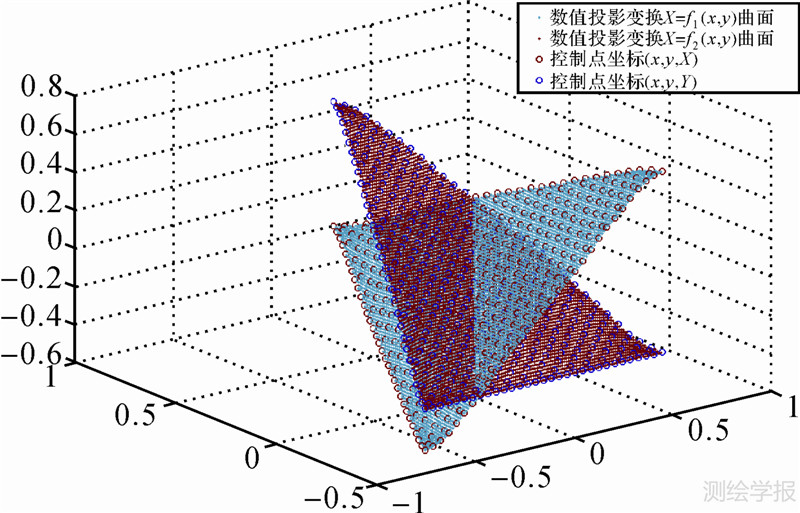
经过3次格网剖分优化计算后,每个球面六边形单元区域的覆盖范围小于5°×5°,根据文献[14]的试验表明,将上述平面规则格网点和对应的球面格网点作为“同名控制点”,采用数值投影变换方法建立两个场之间的数值变换关系,可满足1∶100万地形图精度投影转换的要求。如果精度要求更高,只需采用同样的优化算法计算更深层次的“控制点”即可。这样可以根据用户需求,设计满足不同几何精度要求的球面格网系统。数值投影变换采用二维双谐波样条插值。图 4显示采用第4层406个控制点得到的数值投影转换的变换曲面,蓝色的曲面代表函数X=f1(x,y)的拟合曲面,其上红色的点代表内插的控制点的空间直角坐标系(xi,yi,Xi);红色的曲面代表函数Y=f2(x,y)的拟合曲面,其上蓝色的点代表内插的控制点的空间直角坐标系(xi,yi,Yi),其中(xi,yi)∈平面三角形,i=1,2,…,406。
|
| 图 4 平面三角面到球面三角面的数值投影变换曲面(406个控制点内插曲面) Fig. 4 The surface of numerical projection transformation from planar triangles to spherical triangles (406 pairs control points) |
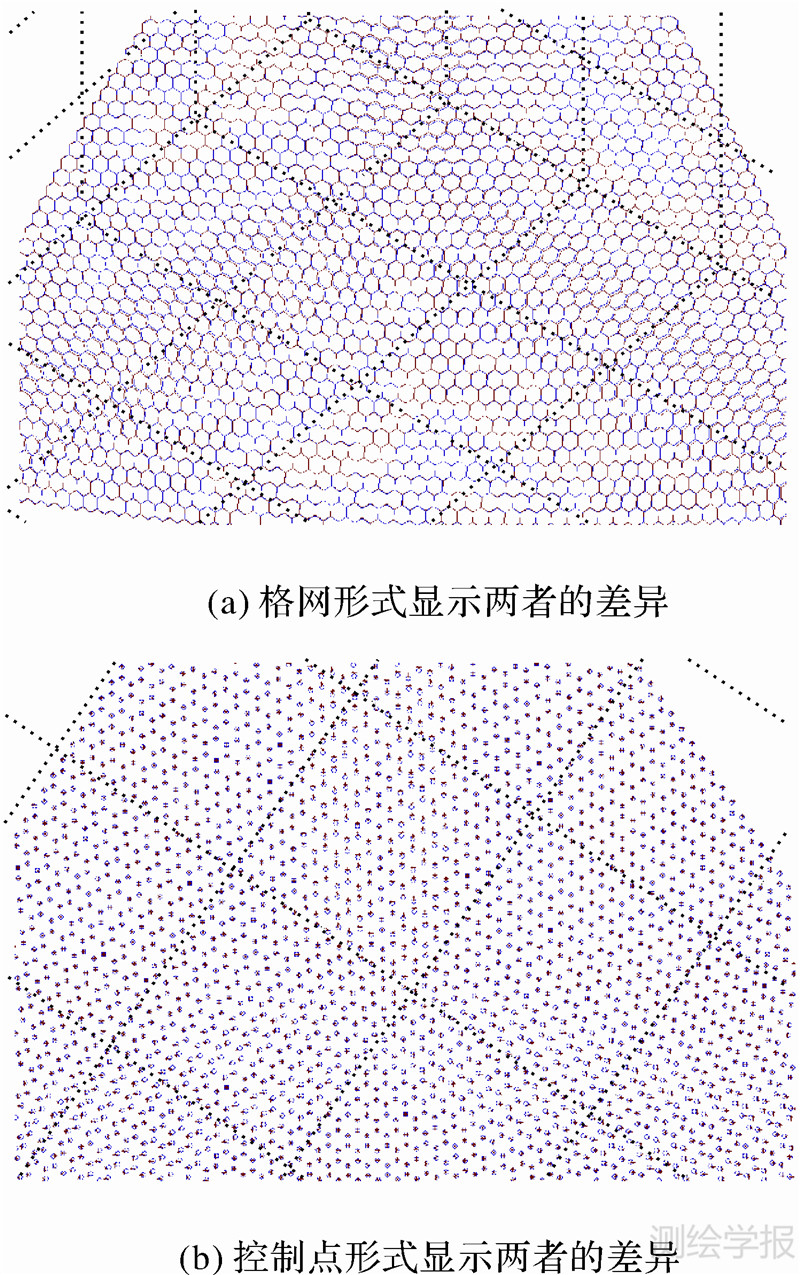
将该数值投影方法与Snyder等积多面体投影[1, 13]比较,图 5(a)中蓝色的单元和图 5(b)中“°”表示的是采用Snyder投影方式生成的单元和控制点;图 5(a)中红色的单元和图 5(b)中“*”表示的是采用数值投影方式生成的单元和控制点,其中格网的剖分层次n=6。本文提出的数值投影变换构建球面离散格网方法主要是计算点坐标,点计算出来后,球面两点之间的边采用球面大弧连接。
|
| 图 5 分别采用数值投影变换和Snyder等积投影变换得到球面不同的格网和控制点 Fig. 5 The different grids and control points between numerical projection transformation and Snyder equal-area projection |
本文采用数值投影变换进行分面格网控制点转换,理论上在球面二十面体的接缝处会产生断裂。但实际上研究数值投影变换的目的只是为了是构建全球格网,并没有特意去研究数值投影变换本身,可以采用一个非常简单的方法解决该问题。对于4HI剖分方式而言,所有落在球面三角形的边界上的点都不是六边形格网控制的边界点,只是格网边界线的中点或单元中心(如图 2),这些点才会导致接缝处的断裂,而它们对控制球面六边形单元的位置和形状没有作用。只要知道任意六边形单元的边界点,边界点之间连接球面大弧,就构成了球面六边形单元。根据这样的思路,以图 2(b)为例,数值投影变换只需要计算P3、P4、P5、P6的坐标,其他的点根据对称性可以得到,这样就足够连接成球面的格网,无需计算位于三角面边界点上的那些点,这样就不可能出现格网的裂缝。当然根据用户的需要,处于三角面边界上的那些点可以根据三角面间的对称性进一步计算得到,例如P3P7⊥ASBS可求得P7。
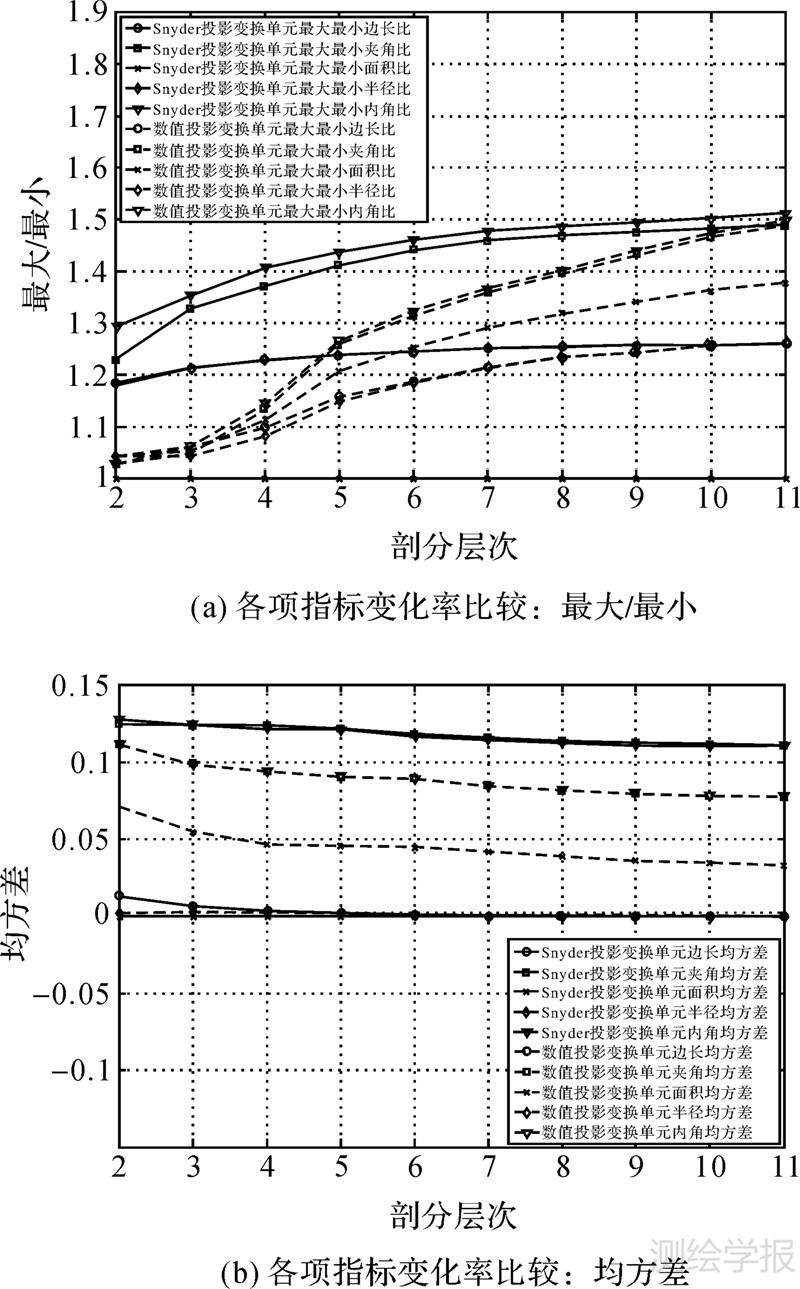
下面的试验针对剖分层次处于n=2~11层的球面离散格网,分别采用采用数值投影变换和采用Snyder等积投影变换生成不同层次离散格网,并比较其几何属性,包括单元边长的变换率、夹角的变化率、面积的变化率、单元半径的变化率(每个单元中心到边界距离均值的变化率)、单元内角的变化率(每个单元边界与中心成的角,一个单元有6个内角,不考虑五边形单元的情况),这些属性从客观上衡量了球面离散格网的均衡性。图 6是这些指标的统计曲线情况。
|
| 图 6 数值投影变换和Snyder等积投影变换生成离散格网的各项几何指标变化率比较图 Fig. 6 The geometrical properties of generating grids between numerical projection and Snyder equal-area projection |
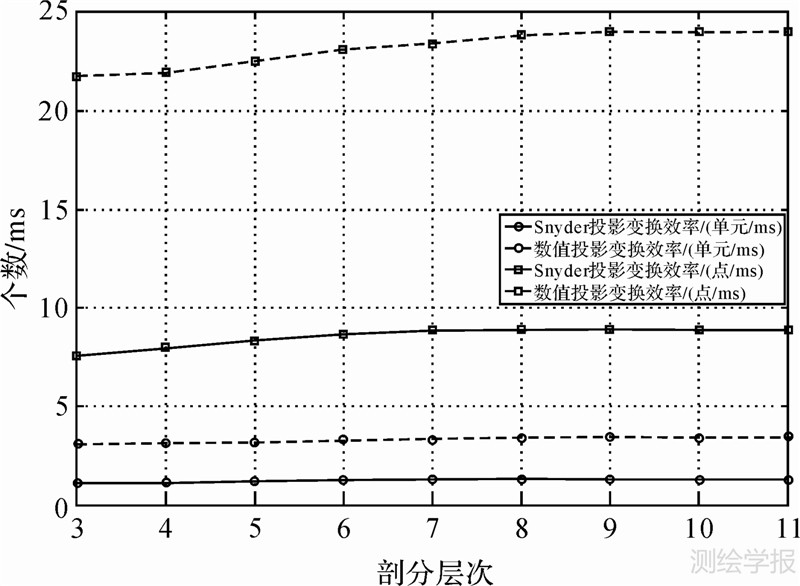
图 7比较了采用数值投影变换和Snyder等积投影变换这两种算法的运算效率,其中时间单位为ms,单元数目指的是一个球面二十面体上的单元数,一个单元需要计算中心点+6个边界点=7个点,所以计算的点数为单元数的7倍。数值投影变换记录的是计算好投影转换参数后,利用式(15)将平面格网转换到球面上的时间,而不包括利用遗传算法等方法计算转换参数的过程,那属于预处理过程,可以作为固定值存储下来备用。
|
| 图 7 数值投影变换和Snyder等积投影变换生成离散格网的效率比较图 Fig. 7 The efficiency curves of generating grids between numerical projection and Snyder equal-area projection |
通过这些试验可以发现,本文提出的采用球面直接最优化剖分结合数值投影变换构造的球面离散格网和现有采用Snyder等积投影变换构造的格网相比,有如下特点:
(1) 相对于Snyder等积投影为基础的球面格网,在边、角变形上要更小,在球面单元面积变形上要大,从单元均匀度比较整体上要优于Snyder等积投影产生的单元;
(2) 利用数值投影变换构建球面格网的过程中,球面控制点和平面控制点可以事先计算好,作为控制文件保存下来,转换的过程中主要是代数多项式运算。因此,在运算效率方面,要高于采用迭代和积分运算的Snyde投影,速度大约是它的2.5~3倍左右;
(3) 由于球面几何变形复杂,随着格网剖分层次的增加,数据精度不断增加,这时采用数值投影变换方法由于控制点相对稀少,导致单元变形开始变大。从图 6的比较发现,当格网层次n>10,采用数值投影变换方式构建的球面格网,其单元的均匀性较Snyder投影变得更差。这时需要增加控制点数目保证数值投影变换的精度,可以采用类似的2.4节的方法,在第4层406个控制点的基础上进行第5层最优化球面剖分,得到更多的控制点,以保证再更高层次的格网在数值投影变换中能保证良好的几何特性。
实际上,对球面直接剖分并不需要无限制地进行下去,因为在球体表面当单元的半径小于某个阈值ρ时,球面效果基本上就已经消失,可以看成是一个平面(例如:在地球表面,半径 <27 km的范围内可以看做是一个平面[21]),因此对于球面直接剖分提供的控制点数目只要能保证数值投影变换后,相应层次的单元变形能够满足用户需求即可。理论上,本文采用的数值投影变换方法理论上可以构造任意两个二维场之间的变换关系,同样也包括建立平面到椭球面的数值变换。为了获取平面与椭球面上的同名控制点,需要对椭球面进行初始剖分。但是,椭球面在直接剖分的情况下,与大圆性质相似的测地线并不存在解析解,构造式(4)中的理想椭球面正多边形存在困难,较难得到最优化约束下的理想初始剖分,这也正是今后需要重点研究的内容。
| [1] | ZHANG Yongsheng, BEN Jin, TONG Xiaochong.Discrete Global Grids for Geospatial Information: Principles, Methods and It’s Applications[M]. Beijing: Science Press, 2007.(张永生,贲进,童晓冲.地球空间信息球面离散网格——理论、算法及应用[M].北京:科学出版社,2007.) |
| [2] | ZHAO Xuesheng, HOU Miaole, BAI Jianjun. Spatial Digital Modeling of the Global Discrete Grids[M]. Beijing: Surveying and Mapping Press, 2007.(赵学胜,侯妙乐,白建军.全球离散格网的空间数字建模[M].北京:测绘出版社,2007.) |
| [3] | DUTTON G. Improving Locational Specificity of Map Data: A Multiresolution, Metadata-driven Approach and Notation[J]. International Journal of Geographical Information Systems, 1996, 10(3): 253-268. |
| [4] | SAHR K. Location Coding on Icosahedral Aperture 3 Hexagon Discrete Global Grids[J]. Computers, Environment and Urban Systems, 2008, 32(3):174-187. |
| [5] | SAHR K. Icosahedral Modified Generalized Balanced Ternary and Aperture 3 Hexagon Tree:United States, 8229237[P].2012-07-24. |
| [6] | VINCE A,ZHENG X. Arithmetic and Fourier Transform for the PYXIS Multi-resolution Digital Earth Model[J]. International Journal of Digital Earth, 2009, 2(1): 59-79. |
| [7] | PETERSON P. Closed-packed Uniformly Adjacent, Multi-resolutional Overlapping Spatial Data Ordering:United States,8018458[P].2011-09-13. |
| [8] | ZHAO Xuesheng, BAI Jianjun, WANG Zhipeng. An Adaptive Visualized Model of the Global Terrain Based on QTM[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 316-320.(赵学胜,白建军,王志鹏.基于QTM的全球地形自适应可视化模型[J]. 测绘学报,2007,36(3):316-320.) |
| [9] | DAVID A, TODD D, ROSS P. Climate Modeling with Spherical Geodesic Grids[J].Computing in Science & Engineering, 2002,4(5):32-41. |
| [10] | KIDD R. NWP Discrete Global Grid Systems[M]. Austria:[s.n.], 2005. |
| [11] | SAHR K, WHITE D, KIMERLING A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121-134. |
| [12] | TONG Xiaochong,BEN Jin,WANG Ying,et al. Efficient Encoding and Spatial Operation Scheme for Aperture 4 Hexagonal Discrete Global Grid System[J]. International Journal of Geographical Information Science, 2012:1-24. |
| [13] | SNYDER P.An Equal-area Map Projection for Polyhedral Globes[J]. Cartographica, 1992, 29(1): 10-21. |
| [14] | YANG Q, SNYDER P, TOBLER W. Map Projection Transformation: Principles and Applications[M]. London: Taylor & Francis, 2000. |
| [15] | TONG Xiaochong. The Principles and Methods of Discrete Global Grid Systems for Geospatial Information Subdivision Organization [D]. Zhengzhou: Information Engineering University, 2010.(童晓冲.空间信息剖分组织的全球离散格网理论与方法[D].郑州:信息工程大学,2010.) |
| [16] | WU Zhongxing. The Elements of Mathematical Cartography [M]. Beijing: Surveying and Mapping Press, 1989.(吴忠性.数学制图学原理[M].北京:测绘出版社,1989.) |
| [17] | GREGORY M J, KIMERLING J A, WHITE D, et al. A Comparison of Intercell Metrics on Discrete Global Grid Systems[J]. Computers, Environment and Urban Systems, 2008, 32(3): 188-203. |
| [18] | TONG Xiaochong, BEN Jin, ZHANG Yongsheng. The Generation Algorithm for Spherical Voronoi Diagram of Different Aggregation[J].Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 83-89.(童晓冲,贲进,张永生.不同集合的球面矢量Voronoi图生成算法[J].测绘学报,2006,35(1):83-89.) |
| [19] | DAVID T.Biharmonic Spline Interpolation of Geos-3 and Seasat Altimeter Data[J]. Geophysical Research Letters, 1987, 14(2): 139-142. |
| [20] | BRIGGS I C. Machine Contouring Using Minimum Curvature[J].Geophysics, 1974, 39: 39-48. |
| [21] | CHEN Shupeng, ZHOU Chenghu, CHEN Qiuxiao. New Generation of Grid Mapping[J]. Science of Surveying and Mapping, 2004, 29(4): 1-4.(陈述彭,周成虎,陈秋晓.格网地图的新一代[J].测绘科学,2004,29(4):1-4.) |