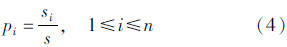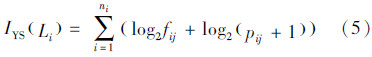1 引 言
近30年来,地图信息的定量度量一直是国际制图学界与GIS界关注的一个基础问题[1]。作为地图上一种典型的线状要素,等高线是地貌的一种主要表达形式,其负载信息的度量被越来越多的学者所关注[ 2, 3, 4, 5]。
现有地图信息定量度量方法大多建立在Shannon信息论基础上,主要是考虑地图符号对象及其邻接关系,计算地图的几何信息和拓扑信息[ 6, 7, 8, 9]。最早Shannon信息论是用来计算符号信息统计熵[ 10, 11]。这种方法最明显的不足是完全丢失了地图最本质的空间位置特征信息。文献[12]提出了地图符号拓扑熵,主要是考虑地图符号的邻接关系,并且仅利用各符号的邻接度计算邻接种类的统计信息,缺乏考虑分布特征等信息。文献[13]从地图符号邻近关系、地图符号分布位置、地图符号分布顺序的角度,分别提出了度量符号分布多样性或差异性的拓扑信息熵、几何信息熵和位置信息熵。文献[14]将地图信息分解为几何信息、拓扑信息和专题信息,并分别提出了Voronoi区域几何信息熵、Voronoi区域拓扑邻近信息熵和专题邻近类型信息熵,该工作是地图信息度量的一个重大突破,但忽略了地图的非完全随机性特征,因而欠缺多样性与差异性分析对地图信息的决定性影响。文献[15]沿用Voronoi区域几何、拓扑信息熵计算,探讨等高线地图信息的度量。事实上,等高线是地形和地貌等信息的表达,因此,等高线信息的定量度量需要与地图所表达的地形和地貌信息的特征相一致。本文采用层次方法,提出一种基于层次划分的等高线信息定量度量的新方法。首先,将复杂的等高线信息度量问题分解为3个层次,单条等高线信息度量层次(即元素层次)、基本地貌单元上邻接等高线信息度量层次(即邻域层次)、全局地图等高线信息度量层次(即整体层次);然后,以地图信息产生的本质为出发点,针对3个层次定义不同的特征描述指标,并建立定量度量方法。
2 等高线信息定量度量的层次化方法研究策略 2.1 地图信息量的度量方法现有地图空间信息量度量方法大都基于Shannon信息论,采用信息熵来度量地图信息[10, 11, 12, 13, 14, 15, 16],表达为
式中,Pi为第i个随机事件发生的概率,且满足 =1。考虑到地图信息来源于地图对象的多样性与差异性,采用一种改进的简化信息量计算方法[17],设V是规范化的特征指标,则信息量I表达为
2.2 层次划分的思想
=1。考虑到地图信息来源于地图对象的多样性与差异性,采用一种改进的简化信息量计算方法[17],设V是规范化的特征指标,则信息量I表达为
2.2 层次划分的思想
从空间认知的角度,阅读一幅地图,通常会按照由粗到精、从整体到邻域再到个体的循序渐进的层次来进行。对于一幅等高线地图,首先关注的是整幅地图的总体地貌分布,如山体或洼地的分布状况等,即等高线地图的整体层次;随后关注的是地形起伏陡缓程度及其变化,这由相邻等高线对的邻近分布决定,本文称之为邻域层次;最后关注更为细节的信息便是单条等高线,如等高线走向的曲折变化,本文称之为等高线地图的元素层次。
从地图描述的角度,元素层次、邻域层次和整体层次分别从微观到宏观描述着等高线图形要素。其中,在元素层次,单条等高线表征了地形剖面的形状,因而可以通过分析等高线的曲折变化来描述。在邻域层次,相邻等高线的间隔距离变化表征了地形的起伏形态,因而可以通过分析相邻等高线的间距变化来描述。在整体层次,等高线簇表征了不同地貌的分布,因而可以通过分析等高线簇的特征差异来描述。地貌分布、地形起伏、剖面形态分布构成地图上等高线信息的来源,并且从上述分析可知,这3个层次的信息来源是相对独立的。
进而,从等高线信息度量的角度,分别选取3个层次具有典型代表性的特征指标,求得所选取的特征指标值的大小,在此基础上计算地图上等高线的信息量,这就是地图上等高线信息定量度量层次方法的研究策略,如图 1所示。

|
| 图 1 基于层次划分策略的地图等高线信息度量方法 Fig. 1 The hierarchical method of measuring the information content of a contour map |
在元素层次上,考虑地图中单条等高线的信息量,这主要取决于等高线的几何形态。等高线几何形态越复杂多变,所反映地表的形态变化越复杂,载负的信息量也越大。等高线越平直或规则,所反映的地表形态越规则,载负的信息量也越小。
3.1 等高线弯曲划分元素层次的等高线信息定量度量的关键问题是合理描述等高线要素的形状。分析等高线形态结构特征可以发现,其多样性和差异性主要表现在两个方面,曲折的存在性与规则性。为此,可以将单条等高线按照“弯曲”进行划分,形成一个有序弯曲的集合。其中,“弯曲”通过等高线上的拐点划分[18, 19]。相邻两个拐点间的曲线段即构成一个弯曲,整条等高线构成弯曲的有序集合。如图 2(a)所示,分别取AB的中点M和CD的中点N为拐点,则相邻拐点M和N之间的曲线段即为一个弯曲,整条等高线成为弯曲的有序集{c1,c2,c3}。如图 2(b)所示,等高线可以分解表达为由7个弯曲组成的有序集{c1,c2,…,c7}。

|
| 图 2 基于拐点的弯曲序列识别 Fig. 2 Identification of bends based on inflection points |
描述弯曲形状特征的指标主要有弯曲的曲线长度、弯曲底线宽度、弯曲进深度、弯曲环绕面积等简单指标,以及由这些简单指标组合得到的复合指标。这里选取弯曲度和弯曲面积比作为弯曲特征指标。对于一条曲线L上的弯曲ci,其弯曲度fi定义为弯曲的曲线长度li与弯曲底线宽度di的比值
式中,n为曲线的弯曲个数。通过分析发现,弯曲度可以有效度量弯曲的形状,但无法区分形状相似的弯曲。选取弯曲面积比辅助度量弯曲特征,可以很好地弥补这一不足。记弯曲ci与弯曲底线所围成区域的面积为弯曲面积si,所有弯曲的弯曲面积之均值为s,定义弯曲面积比pi表达为 分析可知,弯曲度和弯曲面积比的组合作为弯曲特征度量的指标,能够有效地区分不同形状和大小的弯曲。 3.3 基于几何形状的等高线信息量度量对于一幅等高线地图,不妨设有m条等高线,对于其任一条等高线Li,首先按照上述方法进行弯曲划分,得到一个由ni个元素组成的弯曲有序集。对该弯曲有序集中的每一个弯曲cij,采用式(3)和式(4)计算弯曲度fij和弯曲面积比pij。结合式(2),考虑到弯曲度指标以及弯曲面积比指标的值域,单条等高线几何形态表达的地形复杂度信息量可以表达为
从而,元素层次上基于总体地形复杂度的等高线信息为 式中,fij对应于等高线Li经弯曲划分后的第i个弯曲的弯曲度;pij对应于等高线Li经弯曲划分后的第i个弯曲的弯曲面积比;IYS(Li)对应等高线要素Li包含的几何信息量;IYS对应于元素层次等高线信息量。 4 邻域层次等高线信息量度量在邻域层次上,地图上等高线信息由邻域地貌单元的坡度变化传递。地貌单元坡度变化越复杂,其信息量就越大。地貌单元坡度变化的复杂性,一方面反映在平均坡度的变化;另一方面,反映在相邻等高线的形态差异性之上。因此,对于邻域层次的等高线信息量度量,首先将整个地图区域划分为具有特定分布结构的独立地貌单元,然后对单个地貌单元提取平均坡度变化率和相邻等高线的形态信息变化作为特征指标,在此基础上,计算邻域地形起伏形态变化的信息量,即为邻域层次上等高线信息量。
4.1 基本地貌单元的划分基本地貌单元是等高线地图上独立地貌的基本单元。如图 3(a)所示,等高线区域(其中虚线为各等高线Voronoi区域多边形的边)包含4个基本地貌单元,分别用不同灰度级填充表示,见图 3(b)。基本地貌单元可以通过如下步骤划分得到:① 构造等高线的Voronoi图,相邻等高线的邻接程度用邻接度[20]量化表示,定义相邻等高线的Voronoi公共边与对应的较小Voronoi多边形边长的比值为邻接度,于是,邻接度的取值在0到1之间,并且不相邻的两条等高线邻接度为0;② 建立基于邻接度的对偶图,当对偶图中出现分叉或者同一分支上等高线的高程增减变化发生改变时,即为地貌单元边界出现的地方;③ 判断对偶图中的分叉,通过将分叉点归入邻接度最大的分支,并直接划分高程增减发生改变的节点,即可得到等高线地图表达的基本地貌单元。

|
| 图 3 等高线邻接度图划分基本地貌单元 Fig. 3 The division of a contour map to basic landscape units |
邻域层次上,坡度是典型的地形因子,可以较好地描述邻域层次地形的多样性与差异性。选取相邻等高线围成区域的平均坡度变化、相邻等高线几何形态信息变化作为特征指标,进行邻域层次等高线信息量度量。这里,采用相邻等高线和图幅边界共同围成区域的面积与区域中轴线的长度的比值来计算相邻等高线之间的平均坡度,而等高线几何形态信息则通过度量形态差异来得到。
对于一个由mi条等高线组成的地貌单元Ti,按照一定的方向对每相邻等高线围成的区域求取平均坡度sj,由于后续信息量度量仅考虑坡度多样性和差异性,即仅与坡度的相对关系有关,而不涉及坡度绝对值,因而可将sj简化表达为
式中,lj和aj分别为第j条与第j+1条等高线围成区域的中轴线长度和区域面积。对平均坡度指标序列{sj|1≤j<mi}中的每个元素,按其初始自然排列顺序,依次比较相邻两元素的增长特性,分别用-1、0和1表示平均坡度减小、不变和增大(此时可设置一个极小波动范围为定义“坡度不变”的范围),得到坡度增长性序列{diffi},其中,相等的相邻元素构成一个坡段。设该序列包含p个坡段。对该序列采用游程编码,仅顺序记录各个坡段的游程长度,得到游程长度序列{tk|1≤k≤p},第k个元素为第k个坡段包含的邻接等高线对的数目,即相同坡度值所延续的高差跨度。显然,∑tk=mi-1。地貌单元中坡度变化越频繁或复杂,序列{ti}元素越多,其值的差异也越大,地形信息量越大。根据这一规律,记游程平均长度为:t=(mi-1)/p,对tk进行规范化后代入式(2),则可得地貌单元Ti的平均坡度差异性信息量,表达为
对于地貌单元Ti的等高线几何形态特征,可由式(5)计算得到组成Ti的各条等高线基于几何形态的信息量IYS(Lj)。采用与平均坡度指标类似的计算过程,可得等高线几何形态复杂度增长序列为{diffj},对应的游程长度序列为{tk|1≤k≤q},得到相邻等高线的形态差异性信息量为
由此,综合平均坡度和相邻等高线形态的差异性信息量,可得到邻域层次各个地貌单元的地形信息分量。对分解为N个地貌单元的等高线地图,其邻域层次上基于地形坡度变化的等高线信息量可表达为
5 整体层次等高线信息度量从全局的角度,地图等高线是各个基本地貌单元的组合,因而,整体层次上等高线信息通过地貌单元分布的多样性和差异性来传递。地貌类别越丰富,各个地貌单元互异性越大,则载负的信息越丰富。因此,整体层次上等高线信息定量度量需要综合考虑地貌的整体分布及多样性。首先将等高线地图按基本地貌单元进行划分,然后选取地貌单元特征指标并进行量化表达,在此基础上建立基于地貌单元多样性分布的信息度量方法。
通过将地图上等高线基本地貌单元划分,结合等高线的高程值,整个地图区域被分解为不同形态的基本地貌单元的组合。各个地貌单元内等高线数目反映地貌在纵向的跨度即高程差,而地貌单元覆盖面积反映地貌在横向的跨度即覆盖区域,因此,可选取二者为特征指标来度量等高线的整体信息量。
假定等高线地图有m条等高线,被划分为T个基本地貌单元,其中,第Ti个基本地貌单元含有mi条等高线,平均每个基本地貌单元包含的等高线为m=m/T。对等高线数目进行规范化处理后,代入式(2),即可计算得到由地貌单元由高差特征的多样性产生的信息量,表达为
对于地貌单元的覆盖面积特征指标si,仿等高线数目特征指标,可得整体层次上地貌单元覆盖区域的差异信息量IZT(s)为
进而,可得到等高线地图在整体层次上的信息量,表达为分析可以发现,元素层次、邻域层次和整体层次等高线的信息量分别对应不同视角不同类别。因此,可以将地图等高线信息表示为元素、邻域和整体3个层次构成的集合形式
6 试验与结果分析本试验的数据来源于华东某市部分等高线地图。试验中分别截取了相同图幅区域并具有不同地形特征的3个区域1∶1万和1∶5万的等高线,如图 4所示。试验采用ArcGIS Engine 9.3,在Visual Studio 2005 C#.NET开发环境下,进行二次开发实现。试验分别从元素、邻域、整体3个层次定量计算等高线的信息量。同时,结合现有的基于等高线Voronoi区域的信息定量度量方法,计算了等高线几何信息熵和拓扑信息熵。3个区域两个尺度下分层次分类别的信息量计算结果列于表 1。

|
| 图 4 不同地貌等高线图 Fig. 4 Three contour maps of different reliefs |
| bit | ||||||
| 比例尺 | 地形特征 | 经典等高线信息度量方法 | 本文等高线信息度量方法 | |||
| 几何信息 | 拓扑信息 | 元素层次信息量 | 邻域层次信息量 | 整体层次信息量 | ||
| 1∶1万 | 平缓地貌 | 2.54 | 23.74 | 140.24 | 37.82 | 2.49 |
| 略微起伏地貌 | 2.97 | 33.60 | 187.66 | 52.05 | 3.17 | |
| 起伏地貌 | 3.53 | 53.72 | 365.63 | 85.70 | 3.87 | |
| 1∶5万 | 平缓地貌 | 2.14 | 4.54 | 26.53 | 13.54 | 2.27 |
| 略微起伏地貌 | 1.72 | 4.62 | 32.84 | 15.43 | 3.08 | |
| 起伏地貌 | 2.35 | 6.25 | 57.42 | 20.41 | 3.53 | |
比较分析表 1中本文所提出的方法与已有方法的试验结果,可以发现:① 从视觉上看,元素层次上基于等高线几何形态的信息量明显要比邻域层次邻接信息丰富,整体层次的信息是全局的粗糙轮廓信息,其信息含量相对是一个小数值,本文方法的计算结果较好地符合这一视觉认知;② 随着比例尺的减小,信息量也减少,这主要是由细部的信息被平滑掉导致,以上方法的计算结果均较好地符合这一变化规律;③ 随着地形起伏变化程度的增加,基于几何形态的信息量是递增的,而采用已有方法计算1∶1万地图等高线信息量时,能保持正相关关系,但在计算1∶5万地图等高线信息量时,不能保持这种正相关关系;而本文方法能保留不同比例尺之间地形复杂程度的相关性,即地形复杂程度不因比例尺缩放而改变,相应的信息量也保持一致的对比关系。可见,本文方法具有较好的合理性。
此外,在试验中还选取了多个具有不同地形特征地区的等高线地图,采用本文提出的方法进行了信息量计算,所得结果很好地符合实际地形的空间认知。从试验结果分析,元素层次的信息量最丰富,邻域层次的信息量次之,整体层次的信息量最少。从认知角度分析,元素层次反映微观的纹理特征,整体层次反映宏观的地貌构成,而邻域层次反映中观的相邻和比较关系。可见,试验结果较好地符合认知。对于单个层次的信息量,分析可以发现:① 等高线形态越曲折多变,地图的细部特征越丰富,地形越复杂,其元素层次的信息量越丰富;② 邻近等高线形态差异越大,相邻等高线间的关系越复杂,地形越多变,邻域层次的信息量越丰富;③ 区域独立地貌单元越多,地貌形态越多样化,整体层次的信息量越丰富。
为了进一步验证本文提出的3个层次具有相对的独立性,试验中选取基本地貌单元内邻域层次信息量和元素层次信息量进行了对比。如图 5所示,为图 4(b)区域划分得到的独立地貌单元,各个基本地貌单元内等高线邻域层次信息量和元素层次信息量计算结果列于表 2。分析表 2中元素、邻域两个层次的信息量,1号和6号地貌单元以及2号和4号地貌单元,元素层次和邻域层次的信息不是正相关的,说明各个层次之间是不相关或弱相关的,因而这样划分层次对于等高线信息定量度量有必要的。

|
| 图 5 区域基本地貌单元 Fig. 5 The basic landscape units |
| 独立地貌 单元编号 |
等高线 条数 |
元素层次信息 量/bit |
邻域层次信息 量/bit |
| 1 | 11 | 19.35 | 7.53 |
| 2 | 5 | 5.37 | 2.64 |
| 3 | 23 | 29.69 | 8.94 |
| 4 | 4 | 6.36 | 2.02 |
| 5 | 20 | 50.21 | 10.74 |
| 6 | 15 | 20.94 | 5.74 |
| 7 | 21 | 55.74 | 14.44 |
本文结合等高线地图的特点,运用层次划分的思想,从元素、邻域、整体3个层次分别定量度量地图上等高线信息,发展了一种等高线信息定量度量的层次化方法。元素层次的信息量反映细部特征,邻域层次的信息量反映地貌单元内部的差异性特征,而整体层次的信息量反映图幅范围内地貌分布的差异性特征。通过分析和试验验证,本文所提出的等高线地图信息的度量方法,能较好地反映不同地貌及其变化对信息量的影响,并很好地符合人们对等高线地形的空间认知,从而验证了该方法符合信息的产生机理。试验结果说明该方法较现有方法更合理,理论上更为严密,能更好地应用于地形分析、等高线地图综合指导与评价、地图传输控制等诸多方面。
| [1] | WANG Jiayao. Research on the Progress of Cartography and Geographic Information Engineering in China[J]. Bulletin of Surveying and Mapping,2007(5):1-6. (王家耀. 我国地图制图学与地理信息工程学科发展研究[J]. 测绘通报, 2007(5): 1-6.) |
| [2] | OU Weijun, YAO Xianlin. Measuring of Cartographic Information Amount—The General Eigen Value Measuring Method[J]. Map, 1988(4):3-7. (偶卫军, 姚贤林. 地图信息量的测度—综合特征量算法[J]. 地图, 1988(4): 3-7.) |
| [3] | ZOU Jianhua. On the Measuring of Cartographic Information Amount[J]. Journal of the PLA Institute of Surveying and Mapping, 1991(4):72-77.(邹建华. 地图信息计量方法探讨[J]. 解放军测绘学院学报, 1991(4):72-77.) |
| [4] | LIU Honglin. The Study of the Method of Measuring Map Information[J]. Journal of the PLA Institute of Surveying and Mapping, 1992(3):49-55.(刘宏林. 地图信息度量方法的研究[J]. 解放军测绘学院学报, 1992(3):49-55.) |
| [5] | HE Zongyi, BAI Tingying, TENG Yanmin. Determining Varied Information Content of Map with Information Method[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1996, 21(1): 64-68. (何宗宜, 白亭颖, 滕艳敏. 用信息方法确定地图的变化信息量[J]. 武汉测绘科学大学学报, 1996, 21(1): 64-68.) |
| [6] | DENG Min, XU Zhen, ZHAO Binbin, et al. A Transmission Model of Geometrical Information for Individual Spatial Objects in Cartographic Generalization[J]. Journal of Geo-information Science, 2010, 12(5): 655-661.(邓敏, 徐震, 赵彬彬,等, 地图概括中空间目标几何信息传递模型研究[J]. 地球信息科学学报, 2010, 12(5): 655-661.) |
| [7] | WANG Shaoyi, WANG Zhao, DU Qingyun. A Measurement Method of Geometrical Information Considering Multi-level Map Feature[J]. Science of Surveying and Mapping. 2007, 32(4): 60-63. (王少一, 王昭, 杜清运. 顾及地图要素级别的几何信息量量测方法[J]. 测绘科学, 2007, 32(4): 60-63.) |
| [8] | SHANNON C E. A Mathematical Theory of Communication[J]. The Bell System Technical Journal, 1948(27):379-423, 623-656. |
| [9] | HARRIE L, STIGMAR H. An Evaluation of Measures for Quantifying Map Information[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(3), 266-274. |
| [10] | SUKHOV V I. Information Capacity of a Map: Entropy[J]. Geodesy and Aero Photography, 1967, 10:212-215. |
| [11] | SUKHOV V I.Application of Information Theory in Generalization of Map Contents[J]. International Yearbook of Cartography, 1970, 10:41-47. |
| [12] | NEUMANN J. The Topological Information Content of a Map: An Attempt at a Rehabilitation of Information Theory in Cartography[J]. Cartography, 1994, 31(1): 26-34. |
| [13] | BJORKE J T. Framework for Entropy-based Map Evaluation[J]. Cartography and Geographical Information Systems, 1996, 23(2): 78-95. |
| [14] | LI Z L, HUANG P Z. Quantitative Measures for Spatial Information of Maps[J]. International Journal of Geographical Information Science, 2002, 16(7): 699-709. |
| [15] | LIU Wenkai, QIAO Chaofei, CHEN Yunhao, et al. Quantitative Measures for Spatial Information of Contour Maps[J]. Geomatics and Information Science of Wuhan University, 2008, 33(2): 157-159, 176. (刘文楷, 乔朝飞, 陈云浩,等. 等高线图信息定量度量研究[J]. 武汉大学学报:信息科学版, 2008, 33(2): 157-159, 176.) |
| [16] | SHANNON C E. A Mathematical Theory of Communication[J]. The Bell System Technical Journal, 1948(27):379-423, 623-656. |
| [17] | WHELAN B M, MCBRATNEY A B. Prediction Uncertainty and Implications for Digital Map Resolution [C]//Proceedings of the Fourth International Conference on Precision Agriculture.Madison:[s.n.], 1998:1185-1196. |
| [18] | WU Hehai. Automatic Determination of Inflection Point and Its Applications[J]. Geomatics and Information Science of Wuhan University, 2003,28(3):330-335.(毋河海. 数字曲线拐点的自动确定[J]. 武汉大学学报:信息科学版, 2003, 28(3): 330-335.) |
| [19] | GUO Qingsheng, HUANG Yuanlin, ZHANG Liping. The Method of Curve Bend Recognition[J]. Geomatics and Information Science of Wuhan University, 2008,33(6):596-599.(郭庆胜, 黄远林, 章莉萍. 曲线的弯曲识别方法研究[J]. 武汉大学学报:信息科学版, 2008, 33(6): 596-599.) |
| [20] | LIU Jianjun, CHEN Jun, WANG Donghua, et al.The Study of Description and Application of Contour Adjacency Relationship[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 174-178. (刘建军, 陈军, 王东华,等. 等高线邻接关系的表达及应用研究[J]. 测绘学报, 2004, 33(2): 174-178.) |