2. 现代工程测量国家测绘局重点实验室,上海 200092
2. Key Laboratory of Modern Engineering Surveying, SBSM, Shanghai 200092, China
1 引 言
文献[1]提出了建立在EIV模型上的TLS概念,并将其应用于数值分析计算中,随后文献[2]将总体最小二乘算法推广,并完善了文献[1]提出的总体最小二乘算法,得到了广义总体最小二乘求解算法。近几年,TLS算法在测量模型的建立及数据处理上均得到了较为广泛地应用。文献[3]提出基于TLS方法的球靶标定位方法;文献[4]利用加权总体最小二乘(WTLS)算法对平面靶标及球靶标进行拟合;文献[5]利用TLS方法建立了更加可靠的坐标转换系统。以上应用均是基于模型中系数矩阵与观测量矩阵均含有误差的情况,通过建立EIV模型来求得更加可靠的解算结果,但并没有考虑系数矩阵病态的情况。另一方面,在传统最小二乘方法(LS)中,由于系数矩阵的病态性进而会导致因观测量的微小波动而造成解算结果产生巨大的波动。文献[6]提出的正则化理论以及文献[7]提出的截断奇异值(TSVD)的办法通常被用来解决线性估计下LS的病态问题。显然,病态性的问题同样也可能存在于TLS的解算中。文献[8]利用广义奇异值分解(GSVD)的办法得到了TLS的截断奇异值解法(T-TLS);文献[9]推导并证明了总体最小二乘正则化算法(R-TLS)的可靠性;随后,文献[10, 11, 12]也相继推导并证明了多种形式的R-TLS方法。国内对病态总体最小二乘的分析及其在测量数据处理中的应用还不多,相关文献也较少。文献[13]推导了病态总体最小二乘模型的正则化迭代算法;文献[14]基于平差模型推导了加权病态总体最小二乘的岭估计算法。文献[13, 14]中对病态总体最小二乘问题的处理主要是基于文献[15]的推导基础及经典最小二乘平差理论,正则化参数的选择则主要以文献[16]提出的L曲线法为基础,求解结果为总体最小二乘的标准正则化解,较之文献[16]提出的最小二乘正则化L曲线法所得到的结果并无明显地提高。
基于文献[9]提出的R-TLS的思想以及文献[10, 11]的分析结果,结合文献[16]提出的L曲线法的思想,本文探讨了病态总体最小二乘的一种广义正则化方法(R-GTLS)。通过数值算例结果表明该方法在处理病态总体最小二乘问题时,较之R-LS与R-TLS有较明显的优势。最后本文对该方法进行了详细的总结。
2 病态总体最小二乘的分析及正则化模型本文所采用的线性估计基础模型为
式中,A为系数矩阵;b为观测量矩阵;x为待求参数。针对误差仅存在于观测量矩阵b中,而系数矩阵A中不含误差的情况,最小二乘求解约束条件可表达为
总体最小二乘方法相对于最小二乘方法建立了更加可靠的EIV模型,将误差同时合理地分配于系数矩阵与观测量矩阵中,其求解约束条件可表达为
A#、b#为不含误差的系数矩阵及观测量矩阵。基于以上约束,基础模型的最小二乘解和总体最小二乘解分别为[1, 2]
式中,σn+1为增广矩阵[A b]的第n+1个奇异值;I为单位阵。由病态最小二乘理论分析可知,当系数阵A存在接近于0的奇异值时,其矩阵条件数很大,造成基础模型求解的病态。在最小二乘的求解中具体表现为法方程求逆时产生的病态。对于总体最小二乘病态问题,基于数值分析理论的观点,其求解过程为一个降正则化的过程,因此将造成更大的条件数,在求解中可能会出现更加病态或不稳定的结果。基于数理统计理论的观点,总体最小二乘方法在求解中通过减去1个系数误差的近似协方差阵(σn+1I)来达到在一定程度上去除法矩阵ATA中偏差的效果,进而得到相对稳定的解[17]。
根据系数阵A的奇异值分布特点,可将病态情况分成两类[18],第1类为奇异值呈阶梯状分布,即在某处存在明显的跳变。根据文献[16]的分析,该类病态处理可用TSVD的办法加以克服。同样,这类病态问题也可使用T-TLS的办法加以解决。与TSVD针对系数阵A的奇异值分解不同的是,T-TLS针对的是增广阵[A b]的奇异值分解,并且根据文献[8]的分析,T-TLS在大部分情况下可以得到比TSVD更加理想的解算结果。第2类病态问题中奇异值的分布呈现逐步衰减的过程,该类病态问题的解决主要采用的是Tikhonov正则化方法。本文主要探讨第2类病态问题下的总体最小二乘问题。
Tikhonov正则化理论下的最小二乘模型为
式中,δ为正常数;L通常为基于1次或2次偏导数的约束矩阵。在不等式约束条件下,建立Lagrange多项式[9]
式中,λ为Lagrange因子。在该表达式中求解参数x,并满足式(5)。当δ足够小时,解参数x满足如下目标函数
此时,λ即为正则化因子。根据最小二乘的正则化模型,建立总体最小二乘下的Tikhonov正则化模型为
相应的Lagrange多项式为
式中,μ为Lagrange因子。同样假定δ足够小,得到与式(7)相类似总体最小二乘解满足的目标函数
式中,ζ为R-TLS下的正则化因子。根据文献[9]的推导可知式(9)的总体最小二乘正则化解(R-TLS) xR-TLS满足
式中
在式(8)中,若L=I则式(11)可相应转换为Tikhonov正则化的标准形式
式中,λIL=λI+λL,式(12)可以看做是总体最小二乘的岭估计方法[13]。据文献[9]的分析知,当δ<‖xLS‖2,总体最小二乘的标准Tikhonov正则化方法得到的解与最小二乘正则化方法的解在数值上相差不多,其求解精度相当。文献[10]提出,病态情况下解的2次范数‖LxLS‖2和‖LxTLS‖2 将会很大,此时选择相对较小的δ并容易满足 δ2<‖LxLS‖22,则可用等式代替式(8)中的不等式得到如下约束条件
在式(13)中若L=I,即成为式(12)中的标准正则化形式,1+‖x‖22可被1+δ2替代,当δ足够小时约束条件将退化为最小二乘下的正则化条件。这也说明在处理病态总体最小二乘问题时,标准正则化方法相对最小二乘正则化方法将无明显优势,并且将削弱总体最小二乘方法相对最小二乘方法在数理统计方面的优势。因此在处理病态总体最小二乘问题时应考虑选择非标准正则化的方法。
根据最小二乘正则化L曲线选参方式可知,假设δ足够小,那么对于式(7)不必已知δ的确切值,通过L曲线的方式来权衡‖b-Axλ‖2与‖Lxλ ‖2 的比重,从而选择合适的正则化参数λ。对于式(10)的约束条件,假设先验条件δ也足够小,那么同样可以找到合适的λL,计算出λI的值,从而由式(11)得到总体最小二乘正则化的解xR-TLS。根据文献[16]提出的L曲线法的思想,对于总体最小二乘而言,残差范数式将变为: 。下面给出本文提出的一种广义正则化方法的具体算法。
。下面给出本文提出的一种广义正则化方法的具体算法。
首先在一定的范围[a,b]内给定λL的值,计算出R-TLS的解xλL 。在对数域内做出L曲线图,剔除L曲线中‖Lxλ ‖2值较大的部分曲线,以此保证先验信息δ足够小。基于文献[16, 18]对L曲线图特点的分析可知,在拐点处点的密度将明显高于其他部位,所以本方法选择L曲线点位密集的拐点处对应的解xλL 作为病态总体最小二乘正则化的解xR-TLS。具体迭代步骤如下:
(1) 给定λL取值范围,和约束阵L。
(2) 按一定步长选取λL,得到最小二乘正则化解,利用式(11a)求λI的初始值。
(3) 按式(11)求解xλL ,并利用式(11a)更新λI。
(4)利用更新的λI再次更新xλL ,重复步骤(3)、(4)直至收敛,步骤(4)收敛后跳到步骤(5)。
(5) 重复步骤(2)、(3)、(4),得到新的1组λL、λI、xλL 收敛值。得到所有收敛值后跳到步骤(6)。
(6) 利用 与‖LxλL‖22做出L曲线图。
与‖LxλL‖22做出L曲线图。
(7) 选择拐点,得到相应的λL,此时得到的解即为广义正则化解xλL=xR-GTLS。
3 数值算例使用文献[19]“Regularization Tool 2007”中的3组病态试验数据来测试本文所提出广义正则化方法。在算例中同时对系数矩阵及观测量矩阵加入不同程度的扰动误差,并分别用R-LS,R-TLS和本文提出的R-GTLS 3种方法求解,从而探讨R-GTLS求解的优势。算例中广义正则化方法中所使用的约束矩阵L均选取一阶的偏导矩阵[18]。
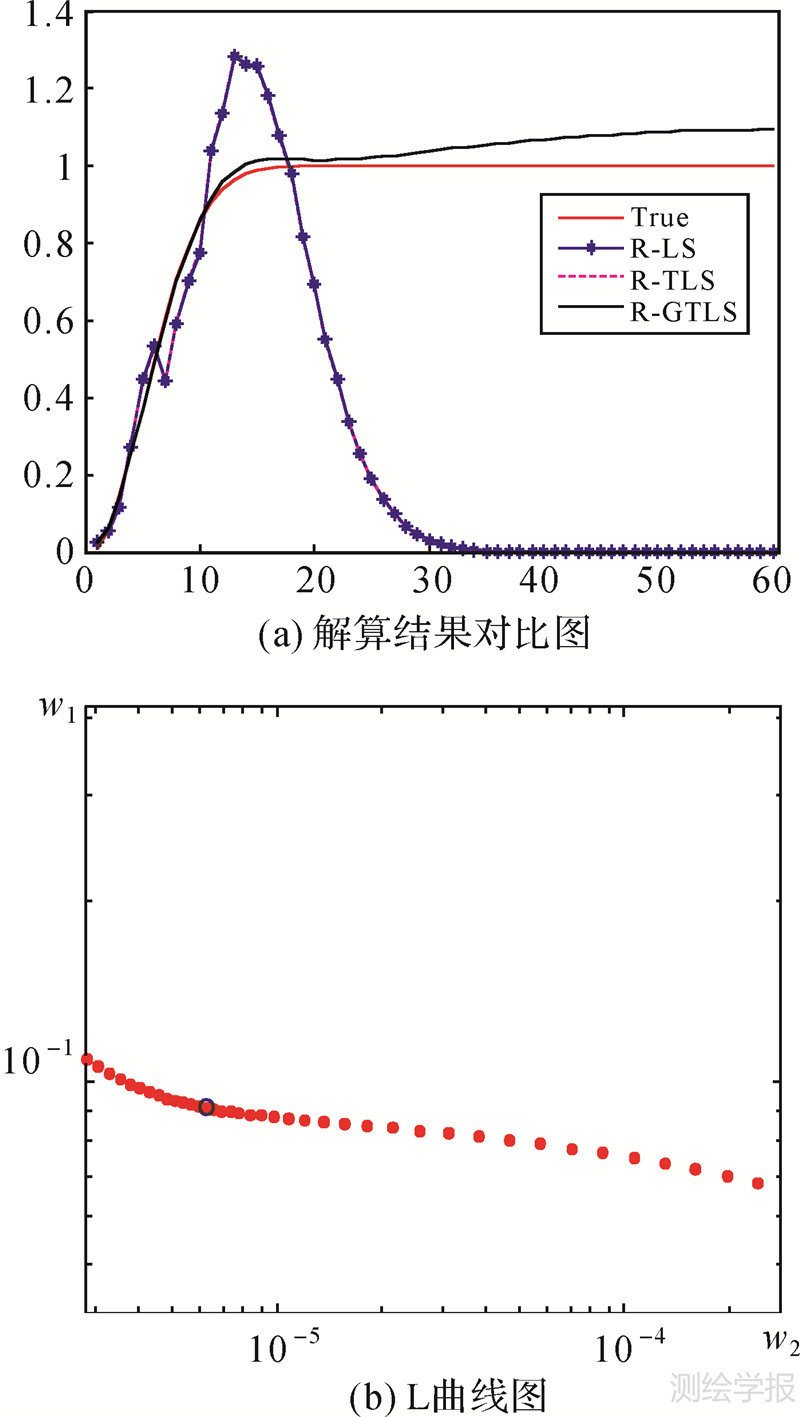
算例1:采用文献[19]“Regularization Tool 2007” 病态模拟数据 “i_laplace”。 其中,条件数的数量级为1033,很明显该问题为严重病态问题。系数阵和观测向量的每一个元素上均加以该元素大小的百分之一的随机扰动误差,用以模拟数据中存在的观测误差。图 1(a)分别给出了真值x(红色线),R-LS求解值(蓝色“*号”线),R-TLS求解值(粉色线),和R-GTLS求解值(黑色线)。图 1(b)给出了R-GTLS求解中L曲线图及拐点选择处(蓝色圈),其中 。
。
|
| 图 1 不同方法对比及拐点选择 Fig. 1 Comparison of different methods and inflection point selection |
表 1分别列出了这几种方法求解的偏差范数‖Δx‖2与相对偏差范数 。
。
| R-LS | R-TLS | R-GTLS | |
| ‖Δx‖2 | 6.070 6 | 6.072 2 | 0.433 5 |
 | 0.839 8 | 0.840 0 | 0.060 0 |
算例2:问题同算例1,但将系数阵和观测向量的误差扰动缩小到对应元素大小的千分之一。图 2中注释同图 1。

|
| 图 2 不同方法对比及拐点选择 Fig. 2 Comparison of different methods and inflection point selection |
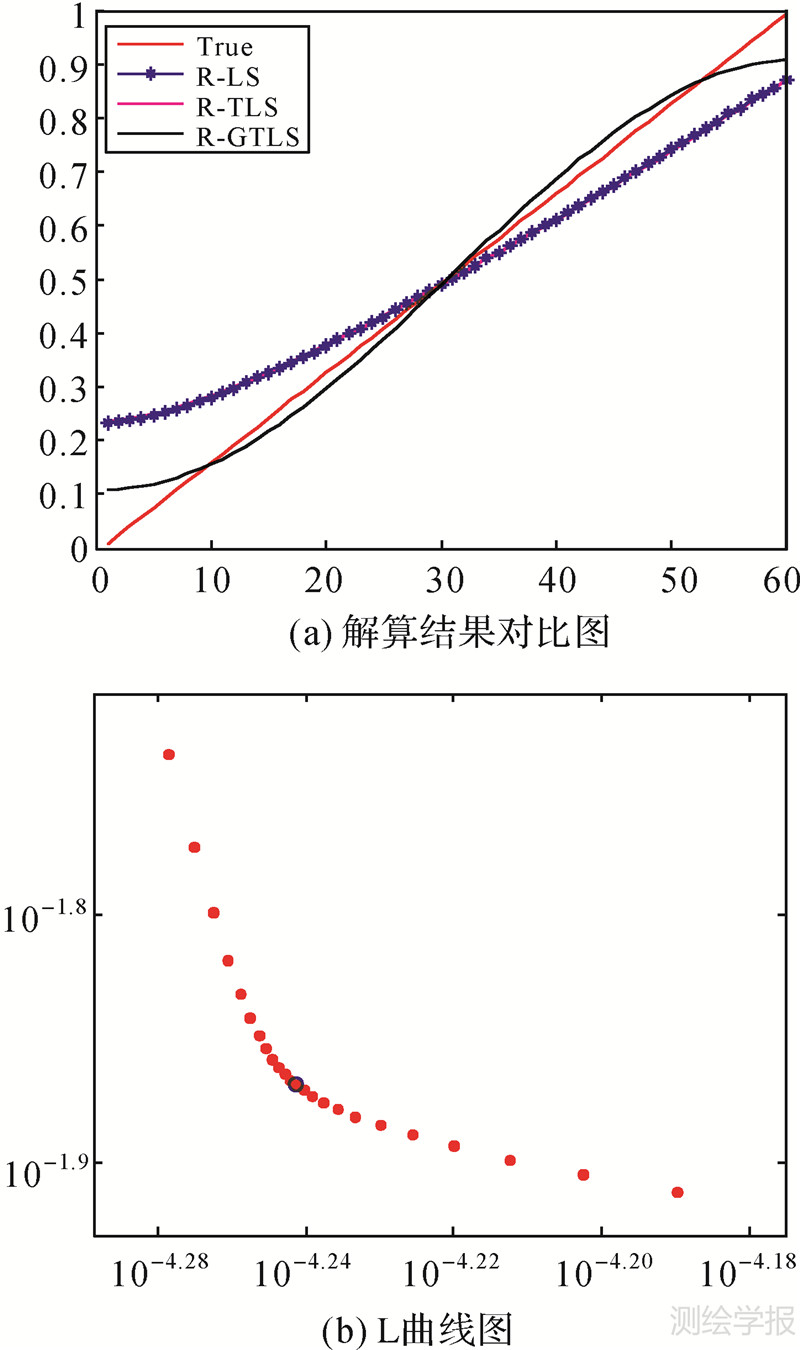
算例3: 采用文献[19]的病态模拟数据 “foxgood”。其中,病态条件数的数量级为105。系数阵和观测向量的每一个元素上均加以该元素大小的百分之一的随机扰动误差,用以模拟数据中存在的观测误差。图 3中注释同图 1。
|
| 图 3 不同方法对比及拐点选择 Fig. 3 Comparison of different methods and inflection point selection |
通过以上3组算例可以看到,在偏差范数指标上R-LS与R-TLS求解结果差值不大,但R-GTLS求解结果的偏差范数明显小于前两者。同样相对误差指标也表明在处理病态总体最小二乘问题时R-TLS解相对与R-LS解并无明显优势。
通过表 2与表 1对比可以发现,当病态性指标相近时,误差成倍增长将导致R-LS与R-TLS求解结果偏差增大;R-GTLS的求解结果偏差也随误差的增大而增大,而且较前两种方法更加敏感,但结果明显优于前两种方法,R-GTLS的偏差范数指标较之R-LS与R-TLS方法所得到的结果均减小了一个数量级,即更加接近真值。相比之下,相对偏差变化不大,但R-GTLS较R-LS与R-TLS变化更为敏感。对比表 1与表 3可以发现,当添加的扰动误差相近时,病态性的严重程度将对求解结果产生很大的影响,尽管此时R-LS与R-TLS求解结果同样相差不大,但当病态性增强时,其解的偏差范数成倍增加。 R-GTLS的解在该两种情况下均明显优于另外两种方法的解,并且在抵抗病态程度方面,其稳定性也好于其他3种方法。
| R-LS | R-TLS | R-GTLS | |
| ‖Δx‖2 | 5.939 0 | 5.888 0 | 0.199 1 |
 | 0.821 6 | 0.814 6 | 0.027 5 |
| R-LS | R-TLS | R-GTLS | |
| ‖Δx‖2 | 0.736 2 | 0.745 1 | 0.260 4 |
 | 0.164 6 | 0.166 6 | 0.058 2 |
下面给出一组测边网的算例,同时运用不同方法进行解算,进而探讨R-GTLS在测量数据处理中的优势。
算例4:采用文献[20]模拟的空间测边网算例。P1、P2、…、P10为10个已知点,其坐标具体数据略去。10个已知点到3个未知点P11、P12、P13 (假设它们的模拟坐标分别为(0,0,0)、(68,-26,9)和(14,41,-11) )的观测距离也给出,并且3个未知点间的距离也同时测量得到。假设各距离为等精度观测,测距中误差为±0.01 m。该问题归结为,根据33个边长观测值确定3个未知点的坐标。计算中,3个未知点的坐标近似值分别取为(0.01 m,-0.01 m ,0.00 m)、(68.01 m,-25.99 m,8.98 m)和(14.02 m,40.99 m,-11.01 m)。通过文献[20]可以知道,该测边网观测方程的系数阵A严重病态,法矩阵条件数为89 543。表 4给出各算法结果及误差范数等。
| 真值 | LS | R-LS | TLS | R-TLS | R-GTLS |
| 0 | 0.053 1 | 0.052 3 | -0.487 4 | 0.040 5 | 0.018 2 |
| 0 | -0.084 6 | -0.069 9 | -0.158 7 | -0.011 7 | -0.002 7 |
| 0 | -0.854 5 | -0.679 8 | -202.271 3 | -0.046 3 | 0.006 2 |
| 68 | 68.039 6 | 68.040 6 | 66.593 3 | 68.029 1 | 68.015 3 |
| -26 | -26.095 3 | -25.905 2 | -387.407 9 | -25.935 1 | -25.985 1 |
| 9 | 8.281 9 | 8.948 2 | -1264.034 9 | 8.965 4 | 8.983 7 |
| 14 | 14.007 4 | 14.007 8 | 14.078 8 | 14.008 9 | 14.002 6 |
| 41 | 40.906 4 | 40.946 8 | 384.314 5 | 40.967 7 | 40.992 0 |
| -11 | -11.269 6 | -11.123 3 | 1075.662 0 | -11.010 2 | -11.007 8 |
| ‖Δx‖2 | 1.161 0 | 0.707 9 | 1758.081 0 | 0.106 8 | 0.035 1 |
 | 0.013 5 | 0.008 2 | 20.466 3 | 0.001 2 | 0.000 4 |
由表 4可以看到,尽管总体最小二乘法在处理系数矩阵含有误差的模型时有较好的统计优势,但当系数矩阵出现病态时,总体最小二乘法受病态的影响也将更加严重。其次,R-TLS的结果较之R-LS的结果在偏差范数上有一定程度的减小,但两者均大于厘米级的观测中误差。R-GTLS将偏差范数很好地控制在厘米级,与测距中误差水平相当。同时R-TLS将相对误差提高到了千分之一,而R-GTLS将其提高到万分之四的水平,其优势比较明显。另外,在例4中,坐标初值如果偏差较大,以上5种方法的结果都比较差,但本文的方法相对来说是最好的,可以将误差量级稳定在初值误差量级上,而其他4种方法都会将误差扩大几十倍甚至百倍。这表明在网行较差的特殊边角网下,处理系数矩阵病态的正则化方法对初值的依赖比较严重。
4 结 论在总结现有病态最小二乘和整体最小二乘的求解方法的基础上,重点分析了病态整体最小二乘正则化解法,提出了一种新的正则化算法。通过本文研究可以得到以下3点结论:
(1) 在利用正则化方式处理病态总体最小二乘问题时,标准正则化方法(R-TLS)较之最小二乘正则化方法(R-LS)没有明显的优势,其求解效果与最小二乘求解效果相当。
(2) 通过数值算例可以看到,R-LS与R-TLS求解结果在偏差范数及相对偏差范数上没有较大的差距。但是R-GTLS的求解结果明显好于R-LS与R-TLS。
(3) R-GTLS方法较之R-LS方法与R-TLS方法能更好地抵抗因病态所造成的解的不稳定性,而且对于误差干扰减少时其求解改善的敏感程度也高于其他两种方法。
| [1] | GOLUB G H, LOAN F C VAN. Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893. |
| [2] | HUFFEL S VAN, VANDEWALLE J. Analysis and Properties of the Generalized Total Least Squares Problem AX=B when Some or All Columns of A are Subject to Errors[J]. SIAM Journal on Matrix Analysis and Applications, 1989, 10(3): 294-315. |
| [3] | LU Tieding, ZHOU Shijian, ZHANG Liting, et al. Sphere Target Fixing of Point Cloud Data Based on TLS [J]. Journal of Geodesy and Geodynamics, 2009, (4):102-105. (鲁铁定,周世健,张立亭, 等. 基于整体最小二乘的地面激光扫描标靶球定位方法[J].大地测量与地球动力学,2009, (4):102-105.) |
| [4] | CHEN Weixian, CHEN Yi, YUAN Qing, et al. Application of Weighted Total Least Squares to Target Fitting of Three-dimensional Laser Scanning[J]. Journal of Geodesy and Geodynamics, 2010, (30): 90-96. (陈玮娴, 陈义, 袁庆, 等. 加权总体最小二乘在三维激光标靶拟合中的应用[J]. 大地测量与地球动力学, 2010, (30): 90-96.) |
| [5] | YUAN Qing, LOU Lizhi, CHEN Weixian, et al. The Application of the Weighted Total Least-squares to Three Dimensional-datum Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S):115-119. (袁庆, 楼立志, 陈玮娴, 等. 加权总体最小二乘在三维基准转换中的应用[J]. 测绘学报,2011, 40(S):115-119.) |
| [6] | TIKHONOV A N. Solution of Incorrectly Formulated Problems and the Regularization Method [J]. Soviet Mathematics Doklady, 1963, 4: 1035-1038. |
| [7] | HANSEN P C. Truncated Singular Value Decomposition Solutions to Discrete Ill-posed Problems with Ill-determined Numerical Rank[J]. SIAM Journal on Scientific and Statistical Computing, 1990, 11(3): 503-518. |
| [8] | FIERRO R D, GOLUB G H, HANSEN P C, et al. Regularization by Truncated Total Least Squares[J]. SIAM Journal on Scientific and Statistical Computing, 1997, 18(1):1223-1241. |
| [9] | GOLUB G H, HANSEN P C, O’LEARY D P. Tikhonov Regularization and Total Least Squares[J]. SIAM Journal on Matrix Analysis and Applications, 1999, 21(1): 185-194. |
| [10] | SIMA D M, HUFFEL S van, GOLUB G H. Regularized Total Least Squares Based on Quadratic Eigenvalue Problem Solvers[J]. BIT Numerical Mathematics, 2004, 44: 793-812. |
| [11] | GUO H, RENAUT R. A Regularized Total Least Squares Algorithm[C]//Total Least Squares and Errors-in-Variables Modeling. Amsterdan: Kluwer Academic Publishers, 2002: 57-66. |
| [12] | BECK A, BEN-TAL A. On the Solution of the Tikhonov Regularization of the Regularized Total Least Squares Problem[J]. SIAM Journal on Optimization, 2006, 17(1): 98-118. |
| [13] | YUAN Zhenchao, SHEN Yunzhong, ZHOU Zebo, et al. Regularized Total Least Squares Solution to Ill-posed Error-in-variable Model [J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 131-135. (袁振超, 沈云中, 周泽波, 等. 病态总体最小二乘模型的正则化算法[J]. 大地测量与地球动力学, 2009, 29(2): 131-135.) |
| [14] | WANG Leyang, XU Caijun, LU Tieding. Ridge Estimation Method in Ill-posed Weighted Total Least Squares Adjustment[J]. Geomatics and Information Sciences of Wuhan University, 2010, 35(11): 1346-1350. (王乐洋, 许才军, 鲁铁定, 等. 病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报: 信息科学版, 2010, 35(11): 1346-1350.) |
| [15] | SCHAFFIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421. |
| [16] | HANSEN P C. Analysis of Discrete Ill-posed Problems by Means of the L-curve[J].SIAM Review, 1992, 34(4): 561-580. |
| [17] | MARKOVSKY I, HUFFEL S van. Overview of Total Least Squares Methods[J]. Signal Processing, 2007(87):2283-2302. |
| [18] | HANSEN P C. Rank-deficient and Discrete Ill-posed Problems[M]. Philadelphia: SIAM, 1998. |
| [19] | HANSEN P C. Regularization Tools: A Matlab Package for Analysis and Solution of Discrete Ill-posed Problems[J]. Numerical Algorithms, 1994, 6(1):1-35. |
| [20] | WANG Zhenjie. Regularized Method in Surveying Ill-posed Problem[M]. Beijing: Science Press, 2006: 125. (王振杰. 测量中不适定问题的正则化解法[M]. 北京: 科学出版社, 2006: 125.) |

















