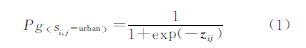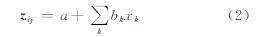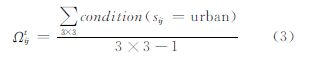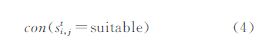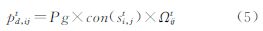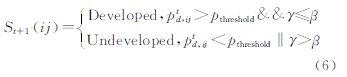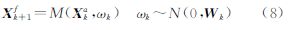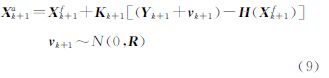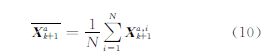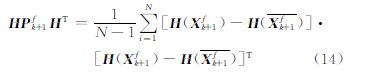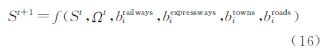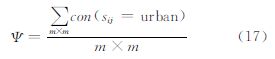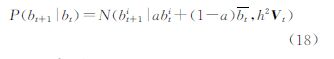2. 中山大学 地理科学与规划学院,广东 广州 510275
2. School of Geography and Planning,Sun Yat-sen University,Guangzhou 510275,China
1 引 言
元胞自动机(CA)由Ulam在20世纪40年代提出,具有强大的空间运算能力[1]。文献[2]中利用CA模拟了一些地理现象后,许多学者不断扩展CA在地理学的应用领域,如城市扩张[3, 4, 5, 6, 7]、山火蔓延[8]、种群变化[9]与荒漠化等[10],并取得了一系列有意义的研究成果。
转换规则的定义是CA模型的核心。在模拟过程中,这些规则决定了元胞状态的变化。传统CA模型的转换规则中的参数是固定的,它们不随模拟过程中的时间和空间改变而变化。在模拟时间尺度跨度较大的复杂地理过程时,模拟的结果难以反映实际情况[8]。例如,在城市发展过程中,由于资源环境约束条件变化和政策等的调整,使得城市空间格局的演变规律在不同经济发展阶段有所变化。利用CA进行模拟预测时,静态的参数组合往往难以反映这种非线性地理过程。
动态调整模型参数的方法被认为能够较好地适应非线性地理模拟,目前已有部分学者开展相关研究。文献[3]提出利用肉眼判断的方法来调整SLEUTH-CA模型参数值。此方法固定其他参数,反复调整某一参数寻求较优模拟结果[3]。当参数较多时,无法使用该方法,而且该方法有一定的主观性。文献[3]中又提出了计算搜索算法。利用计算机计算各个参数组合的模拟结果与实际结果的吻合度,确定最优的参数组合[12]。但这种试验需要高性能工作站运算几百小时。文献[6]提出案例推理(CBR)的CA模型,模型能够根据新的案例动态更新转换规则。但此方法忽略了模拟结果的误差积累。文献[12]提出基于数据同化的CA模型。模型考虑到模型误差的积累,但是没有动态调整转换规则中的参数。总体而言,已有的研究难以在模拟过程中动态调整参数和控制误差积累,这是影响CA模型在复杂非线性地理模拟中应用的主要原因。
近年来兴起的数据同化提供了一种能够利用观测数据自动调整并优化模型状态和参数的方法。它能够融合不同来源、不同精度的直接或间接观测数据,并且集成模型和各种观测因子,自动调整模型模拟轨迹[13, 14]。在数据同化的方法中,非线性滤波方法占有极其重要的地位,其中,集合卡尔曼滤波(EnKF)方法使用最为广泛,在参数优化估计中也有较多的应用[15, 16]。文献[17]对一个二维非线性海风模型进行参数优化估计;文献[18]提出了双集合卡尔曼滤波方法优化水文模型参数;文献[19]在三维的云模型中对模型参数进行优化;文献[20]把联合状态矩阵的方法应用到核污染扩散模型中研究模型参数变化。运用集合卡尔曼滤波方法能够很好地在模拟过程中动态修正模型参数,并且能够在初始参数不准确的情况下快速捕捉参数特征使得被优化的参数收敛于真实值,这为CA模型动态调整模型参数与状态提供了可能。
本文提出了一种基于集合卡尔曼滤波(EnKF)动态优化CA模型参数的方法。该方法先构建由参数和状态组成的联合状态矩阵,再利用观测数据更新联合矩阵,最后把更新后的状态和参数重新输入到模型中进行下一次模拟迭代。文中以广东省东莞市为试验区,模拟其城市扩张,分析了单参数优化情况下参数的有效性,并讨论了在多参数情况下参数收敛情况和城市模拟情景。
2 方 法 2.1 MCE-CA模型在模拟复杂的城市演变过程中,元胞自动机以其“自下而上”、自组织性等优点,被认为是一种非常有效的模拟复杂城市系统的模型[3, 4, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21]。与数学模型相比,CA模型具有简洁的形式并能很好地结合栅格GIS数据。通过定义合适的转换规则,便可模拟出城市的发展情景[3, 4, 5, 6, 7]。研究表明,影响城市扩展的变量主要是空间距离变量,如离商业中心的最短距离、离道路的最短距离等,而这些变量对应的参数值(权重)反映了对模型的“贡献”度[4, 5, 6, 7, 21]。文献[21]运用这些空间变量并提出了多准则的判断(MCE)来表达其他土地类型转变为城市用地的概率
式中,Pg是元胞(i,j)全局性开发概率;Si,j是元胞当前状态;z是描述元胞(i,j)开发特征的向量 式中,a、b为回归模型的系数;x为距离变量。全局性开发概率Pg中考虑到各种空间距离变量对元胞转化的影响,在微观层次上,邻域影响是一个非常重要的因素。它通过一个3×3的核来计算元胞在空间上的相互影响,其计算为
式中,Ωtij是邻域函数;condition是一个条件函数;如果Si,j是城市用地,则返回真(用1表示),否则返回假(用0表示)。在实际中,还应考虑单元约束条件。有些土地类型,如陡峭的山地等不适宜城市发展,而平缓的地区则很适宜城市发展,这里用连续的条件约束来表达
式中,con是土地适宜性评估值(0~1),用连续值可提高模型的科学性与模拟的真实性。综合考虑了全局发展概率,邻域范围和约束条件后,任意元胞在t时刻发展为城市用地的概率可由下式来表达
求出元胞发展概率后,还需要判断此元胞是否发展为城市用地。文中采用阈值法,表达如下
式中,St+1(ij)是元胞(i,j)在t+1时刻的状态;γ为随机变量;β=1/K,K为迭代数。若阈值pthreshold过大,城市形态过于集中;阈值过小,城市形态过于分散。根据文献[4, 21]提出的方案,并通过试验,确定阈值为0.65。MCE-CA模型是模拟城市发展的经典模型。在模型模拟预测时,其假设条件是城市发展模式不随时间变化。实际上,由于政治和经济等因素,城市发展的模式会改变。例如,某城市前期是镇中心扩张发展为主;后期则以沿公路发展为主。在这种情况下,若模型用前期的转换规则来模拟整个时期的城市扩张,模型误差不仅不会消除,还会随着模拟迭代的进行而传递下去。因此,考虑引入集合卡尔曼滤波算法到CA模型中,通过同化观测数据动态更新转换规则中的参数,调整模型运行轨迹,以减少误差积累。
2.2 基于EnKF的数据同化算法集合卡尔曼滤波(EnKF)是文献[16]根据随机动力预报理论而提出的一种顺序同化算法。该算法首先用Monte Carlo方法生成初始集合,然后用集合预报的思想对初始集合进行预测得出预测集合,再把预测集合和观测集合输入到集合卡尔曼滤波更新方程中得到更新后预测集合即分析集合,最后用分析集合作初始集合预测到下一个观测时刻,如此循环。其实现步骤如下:
(1) 初始阶段,模型状态集合初始化。
式中,n为模型状态变量的个数;N为集合的大小;下标0为时间刻度。2) 预测阶段,将分析集合(或者初始集合)输入到模型中,并预测下一个观测时刻k+1得到的预测状态集合。
式中,M为模型算子,本文指元胞自动机模型;Xk+1f是k+1时刻的预测值;Xka是k时刻的分析值,若k=0,Xka为初始集合X0;ωk是期望为0;方差为Wk的高斯白噪声;Wk为模型的误差方差矩阵。(3) 分析阶段,融合预测状态集合和观测集合,并根据集合卡尔曼滤波更新公式,求得分析集合Xk+1a
式中,Yk+1是k+1时刻的状态变量的观测值;H为观测算子;vk+1是期望为0,方差为R的高斯白噪声;N为集合个数。Kk+1为k+1时刻的卡尔曼增益矩阵,其计算如下 式中,R是观测误差协方差矩阵;Pk+1f为状态误差协方差矩阵。 在应用中,常常直接计算Pk+1fHT与HPk+1fHT来减少运算量。(4) 判断是否到结束时刻,若未到,返回步骤(2),否则结束。
集合卡尔曼滤波运用集合预报的思想,把误差统计量的预报隐含在扰动的集合变量中,避免了传统卡尔曼滤波等需要专门对误差协方差进行计算的问题,也解决了卡尔曼滤波应用在非线性系统中的切线性近似的问题。集合卡尔曼滤波不仅简化了矩阵计算,还能利用随机样本的预报值估计协方差得到较高的准确度。
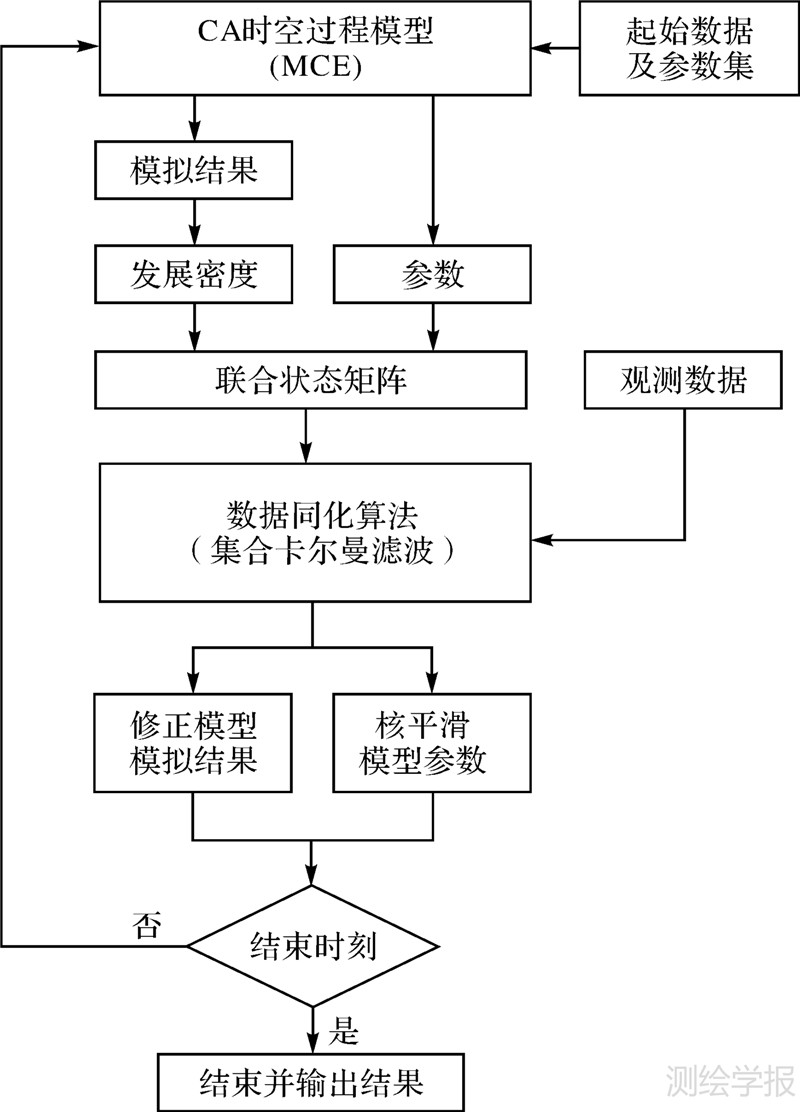
2.3 CA模型的参数优化数据同化方法能够充分利用观测值等信息提高模型模拟精度。引入数据同化方法到CA模型中,笔者进行了初步探索并提出了基于数据同化的CA模型[12]。在该模型的基础上,进一步考虑参数组合对模拟结果的影响,故引入集合卡尔曼滤波的联合状态矩阵方法控制由参数引起的模型误差。该方法主要包括如下几个步骤,其流程如图 1。
|
| 图 1 动态优化CA模型参数流程图 Fig. 1 Flowchart of parameter optimization in CA model |
首先,根据2.1节的描述构建起CA模型并确定需要进行估计的参数。确定的参数包括各个空间距离变量的系数,如公式(2)所示。本文中包括4个,分别是brailways、bexpressways、btowns和broads。运用蒙特卡罗方法生成N(N为EnKF中的集合个数)组不同的参数组合。生成随机参数组合包含两个必要部分,参数初始估计值与参数随机扰动噪声。随机参数集合表示如下
式中,bi为扰动后的参数值;为参数初始估计值;ei为扰动噪声,扰动噪声的分布符合均值为0,标准差为真实值与初始估计值的差的绝对值。其次,把生成的N组不同的参数值输入到CA模型中进行城市模拟,可得出N组不同的模拟结果。此时CA模型可以用如下形式描述
式中,f为定义元胞从时刻t到t+1时刻状态的转换函数;St是t时刻的元胞状态;Ωt是邻域函数;birailways、biexpressways、bitowns和biroads指第i组参数组合中各个空间距离变量的系数值。再次,整合N组参数的模拟结果到状态矩阵中,以计算状态误差协方差。在计算误差协方差前,考虑到CA模型模拟结果只有两种形式(发展与不发展),不能直接参与计算。所以,本文考虑把研究区分成若干个规则的方格,每个方格包含m×m个像元(元胞),用城市发展密度参与数据同化运算。每个方格的城市发展密度为
获得每个方格的城市发展密度后,便可用发展密度来计算误差协方差。同理,观测值也是用发展密度来计算。最后,采用文献[17]中的方法把参数等同于状态,整合N组CA模型参数组合及其模拟结果的发展密度到同一个联合状态矩阵Xj里,即把参数birailways、biexpressways、bitowns和biroads作为状态增加到原有的状态矩阵X中,构成一个包含参数和状态的联合状态矩阵Xj。再将此联合状态矩阵Xj代替X输入集合卡尔曼滤波方法的更新方程(9)中。通过同化观测数据可得到优化后的参数值,并将其输入CA模型,以进行下一时刻的模拟迭代,如此循环。
通过重复上述几个步骤便可实现在模拟过程中动态调整模型参数,进而改变CA模型的转换规则。此外,在集合卡尔曼滤波的分析阶段,也可根据更新方程得出的最优分析场并按照文献[12]的方法对模拟结果进行修正。
3 试验和分析 3.1 数据和模型参数东莞市是珠江三角洲城市化发展中速度最快的城市之一。期间,该区域土地利用变化剧烈、城市扩张速度快,而且还经历多次产业布局调整,城市发展表现出复杂的非线性过程。选择该区域具有典型的研究意义。
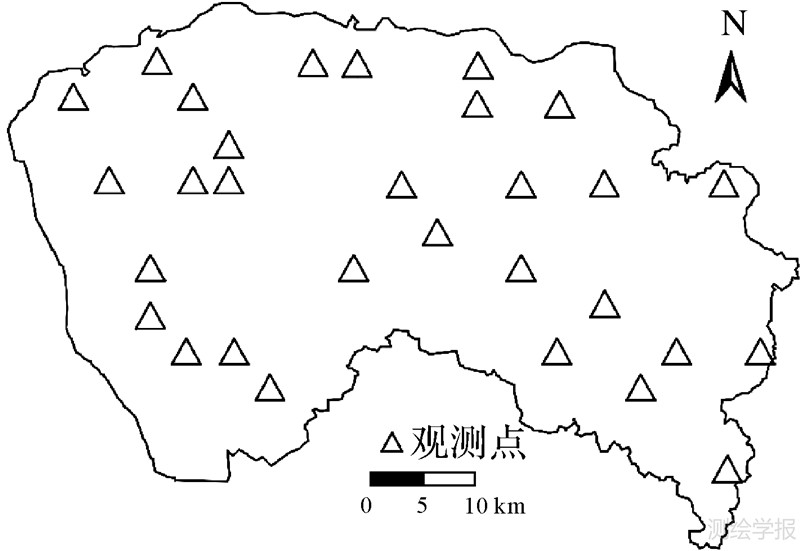
选用模拟起始数据为1993年东莞市遥感TM分类数据。城市发展的距离空间变量有到铁路的距离、到高速公路的距离、到道路的距离和到镇中心的距离(图 2)。运用SPSS软件中的逻辑回归方法对1993—1995年训练样本进行运算得出的各个距离变量的权重(公式(2)中的bk)作为初始参数值。为了观察参数调整后模型误差情况以及方便对所提出的方法进行对比验证,选择观测资料基于如下考虑:若引入多景遥感观测资料来观察参数收敛情况,往往会产生这种情况,纵然获取的参数准确,仍难模拟出“飞地”、“开发区”等人为干预的城市发展用地。而且此时模拟误差主要是由CA根本规则——“邻域发展规则”引起的,难以剥离参数误差与邻域规则误差进行比较验证。若使用较短模拟时间,期间的观测资料又非常难获取。考虑到CA模型在模拟短时段城市发展有较高的精度(本文为87.7%),故文中用模拟的数据代替无法获取的历史观测数据,同时,模拟的观测数据也给参数收敛结果的验证提供了理想的真值。获取观测数据的具体过程如下,首先用SPSS软件中的逻辑回归方法对1993—1997年训练样本进行运算,得出的各个距离变量的权重并作为参数的真值(见表 1)。然后把这些权重输入CA模型中,进行模拟并得出模拟结果,最后把模拟结果转换成发展密度的形式,并选择如图 3所示的30个观测点数据作为观测数据。

|
| 图 2 空间距离变量 Fig. 2 Spatial variables of CA model |
| 待优化参数 | 初始值(1993— 1995年) | 真值(1993— 1997年) | 初始 标准差 |
| 到高速公路距离 | -0.731 | -1.038 | 0.307 |
| 到铁路距离 | 0.601 | 1.184 | 0.583 |
| 到普通公路距离 | -6.094 | -7.089 | 0.995 |
| 到镇中心距离 | -5.423 | -4.597 | 0.826 |
|
| 图 3 观察点空间分布 Fig. 3 Position of observation |
集合(ensemble size)过大,运算量会相当巨大且对结果改善不明显;集合过小,体现不出统计特征并且误差较大[13, 22],本文选择集合大小为30。由于传统CA模型的模拟精度约为80%,故设定模型误差为0.2。观测误差取决于观测数据的精度(87.7%),故设定观测误差为0.13。
除了设置起始模拟数据、初始参数等相关参数外,还需注意生成扰动参数的方差和参数演化控制。扰动参数的方差大小对模型模拟结果的误差统计有极大影响。文中用参数的标准差等于初始误差,初始误差等于初始估计值与真值之差的绝对值。在早期的滤波同化应用中,同化时刻的参数演化常常是将随机扰动加入原参数的集合里生成新的参数集合。此方法往往会由于参数本身的特性导致滤波发散和信息丢失[18]。文献[23]提出了核平滑进行参数更新以避免滤波发散与信息丢失。其参数核平滑表示如下
式中,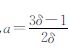 ,δ的取值为(0,1],经验值范围为0.95~0.99;h是平滑衰减系数,
,δ的取值为(0,1],经验值范围为0.95~0.99;h是平滑衰减系数, ;Vt为方差矩阵。
;Vt为方差矩阵。
为了检验联合状态矩阵方法在CA模拟中的适用性,进行了单参数优化试验。在真实的模型参数优化中,往往是多参数同时优化,所以进一步实现了多参数优化,并分析了参数收敛效果与参数优化前后的城市模拟情景。
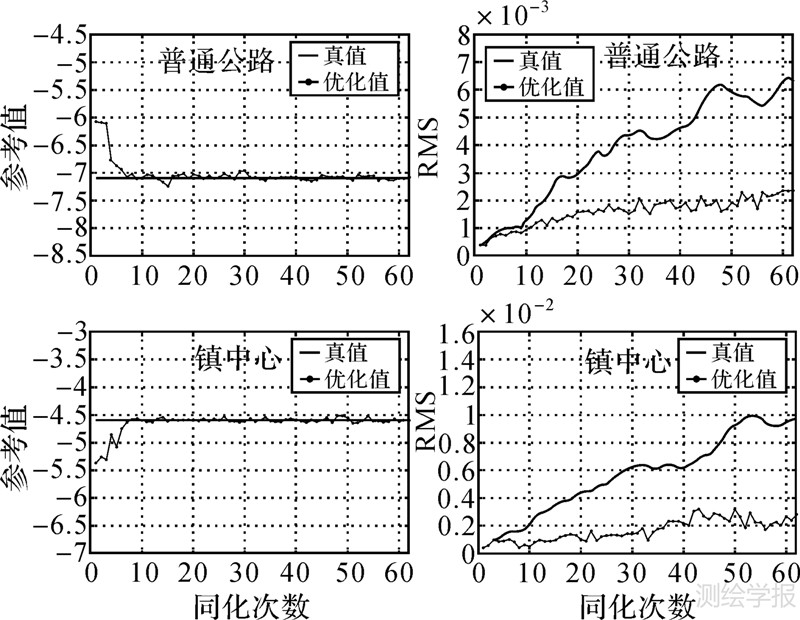
3.2 单参数优化在单参数优化过程中,仅仅被优化的参数按公式(15)进行高斯扰动,其他参数保持真值不变。单参数试验中,模型各个参数优化结果如图 4和图 5所示。除了记录参数优化过程,图中还给出了模拟结果的均方根误差(RMS)。在图例中,“未同化”与“同化后”分别表示未进行参数优化与经过参数优化后的结果。虽然各个参数逼近真值的速度有所差别,但是都能够在较少的同化次数后逼近真值,并在真值的较小范围内波动。各个参数在收敛于真实参数值的时间上显示了一定的相似性,都是在10次同化操作前后收敛于各自的真实参数值。由于各个参数对观测数据的敏感程度不同,所以收敛速度有一所差别。从RMS的变化情况可以注意到,同化后的误差均比没有进行同化的要低。参数“普通公路”与“镇中心”的误差积累约为未同化的1/3,而参数“高速公路”与“铁路”误差只有未同化的1/6。通过动态优化参数和状态,模型能够较好地控制模型误差积累。

|
| 图 4 优化的参数值与RMS变化(1) Fig. 4 Parameter value and RMS in parameter optimization (1) |
|
| 图 5 估计的参数值与RMS变化(2) Fig. 5 Parameter value and RMS in parameter optimization (2) |
在单参数优化试验可以发现,本方法能够在初始参数不准确的情况下快速获得参数特征,并使得被优化的参数收敛于真实值。
3.3 多参数联合优化为了完整地检验集合卡尔曼滤波在优化模型参数的效果,分别进行了两组双参数和一组四参数同时优化的试验。在双参数优化中,被优化的参数进行高斯扰动,其他参数保持真值。两组双参数优化后的模拟精度见表 2,参数收敛情况如图 6所示。结果表明,模拟精度有一定程度的提高,参数收敛情况与单参数优化相似。经过较少次的更新操作后,各个优化的参数均能较快地逼近真值,并在相对较小的误差范围内波动。同时,模型误差RMS均有较大程度的降低。
|
估计的 参数 | 精度/(%) | Kappa系数 | ||||
| 未优化 | 优化后 | 真实参数 | 未优化 | 优化后 | 真实参数 | |
| 高速公路 与铁路 | 87.10 | 87.62 | 0.534 6 | 0.548 4 | ||
| 普通公路 与镇中心 | 87.07 | 87.57 | 87.7 | 0.528 4 | 0.545 7 | 0.550 |
| 所有空间 距离变量 | 87.01 | 87.52 | 0.522 5 | 0.543 0 | ||

|
| 图 6 双参数联合优化的结果 Fig. 6 Parameter values and RMS for two spatial variables |
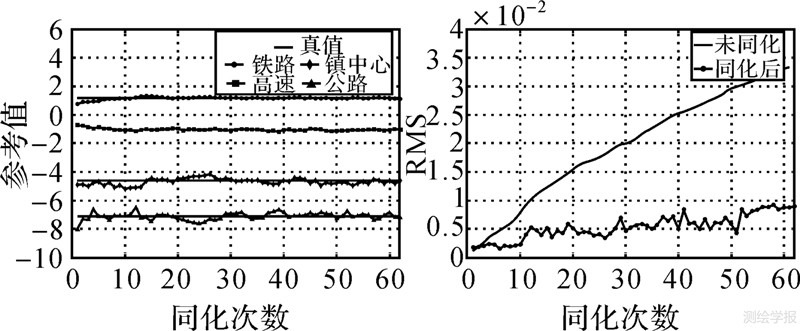
当把优化的参数扩展到所有的参数集合时,各个参数都进行高斯扰动,而且其初始值均偏离真值。通过同化观测资料,笔者得到的结果见图 7与表 2。总体上,各个参数的收敛速度迅速,模型误差较低,模拟精度有所改善。在优化结果中,“高速公路”、“铁路”与“镇中心”3个参数均能较快地收敛,然而参数“普通公路”却一直波动。这主要是由于两个原因:① 与其他参数相比,参数“普通公路”比其他值要大,这就意味着“贡献”大,参数的敏感性强,观测值对参数的变化影响较大,故在一定时间段内出现振荡,需要较多的更新次数来捕捉参数特征;② 在进行数据同化前,将CA模拟结果转换成发展密度,是用均值代替各个元胞状态值,这在一定程度上降低了参数的敏感性。
|
| 图 7 四参数联合优化的结果 Fig. 7 Parameter values and RMS for four spatial variables |
对比模拟结果图(图 8)可以发现,未进行参数优化的模拟结果在市区中南部的大岭山、市区东南部寮步以及研究区的东南部塘厦均有模拟过度的情况。这是由于转换规则的误差引起的,东莞市城市发展前期是围绕城镇中心进行扩张发展,后期沿公路进行发展。未进行优化的CA模型因不能在模拟过程中改变转换规则,会一直以围绕城市中心发展的模式模拟城市演化过程,因此,在某些城镇中心会产生模拟过度的情况。引入集合卡尔曼滤波后,模型能够不断修正转换规则中的参数。修正后的参数能够更好地反映真实情况与各个空间距离变量的关系,因此,参数优化后的模拟结果基本上不存在过度发展的情况。模拟结果与真实参数的模拟结果更接近,也与实际情况很吻合。对比RMS与城市模拟结果,优化后的模拟结果均有一定程度的改善。而且各个参数收敛效果良好,在经过较少次的更新优化操作后,均能够在真值相对较小的误差范围内波动。

|
| 图 8 四参数优化的模拟结果 Fig. 8 Simulation results of four model parameters optimization |
随着参与优化的参数越多,与单参数优化相比,部分参数需要的观测数据会越多。在图 6和图 7中,某些时刻的参数值会突然偏离真值,这主要是由于观测误差引起的,一些观测数据在某些时刻会由于观测误差而偏离真实值,从而导致同化结果也会有一定的误差。虽然部分参数需要较多的同化次数来收敛于真值,但是从总体上,观察数据的选择和观测误差的估计是合理的,从而获取到准确的信息,较好地反映了参数自动优化的整个过程。
4 结 论本文采用集合卡尔曼滤波方法更新CA模型参数与模型状态,并以东莞市为试验区进行模拟试验,得到如下结论:
(1) 本文方法通过构建由模型参数和状态组成的联合状态矩阵,并利用观测数据更新此联合状态矩阵,得出更新后的参数与状态,并将其重新输入到模型中进行下一时刻的模拟。该方法有效地实现了模型参数和状态的动态优化,提高了模型在复杂非线性地理模拟中适应能力。
(2) 单参数和多参数联合优化试验表明,该方法能够很好地优化CA模型参数值并快速收敛于真实参数值,而且还能够有效地减少模型误差。在多参数优化试验中,模拟结果的模拟精度与Kappa系数均有一定程度的提高。
(3) 由于城市发展模式的改变,各个空间距离变量在模拟过程中对模拟结果的“贡献”会变化,即,空间变量对CA模型转换概率的影响会改变。同时空间变量对应权重的不同会引起参数敏感度不同,其参数收敛速度会有所差别。
(4) 空间距离变量对模拟结果有重要的影响,在如何选用合适方法以找寻最优空间变量组合和发展密度网格大小对模型参数的收敛等方面需要作进一步研究。
| [1] | WHITE R, ENGELEN G. Cellular Automata and Fractal Urban Form: A Cellular Modelling Approach to the Evolution of Urban Land Use Patterns [J]. Environment and Planning A, 1993, 25(8): 1175-1199. |
| [2] | TOBLER W R. A Computer Movie Simulating Urban Growth in the Detroit Region [J]. Economic Geography, 1970, 46: 234-240. |
| [3] | CLARKE K C, HOPPEN S, GAYDOS L. A Self-modifying Cellular Automata Model of Historical Urbanization in the San Francisco Bay Area [J]. Environment and Planning B, 1997, 24(2): 247-261. |
| [4] | LI X, YEH A G O. Modelling Sustainable Urban Development by the Integration of Constrained Cellular Automata and GIS [J]. International Journal of Geographical Information Science, 2000, 14(2): 131-152. |
| [5] | LI X, YEH A G O. Data Mining of Cellular Automata's Transition Rule [J]. International Journal of Geographical Information Science, 2004, 18(8): 723-744. |
| [6] | LI X, LIU X P. An Extended Cellular Automaton Using Case-based Reasoning for Simulating Urban Development in a Large Complex Region [J]. International Journal of Geographical Information Science, 2006, 20(10): 1109-1136. |
| [7] | LIU Xiaoping, LI Xia. Fisher Discriminant and Automatically Getting Transition Rule of CA [J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 112-118. (刘小平, 黎夏. Fisher判别及自动获取元胞自动机的转换规则[J]. 测绘学报, 2007, 36(1): 112-118.) |
| [8] | CLARKE K C, BRASS J A, RIGGAN P J. A Cellular Automata Model of Wildfire Propagation and Extinction [J]. Photogrammetric Engineering & Remote Sensing, 1994, 60: 1355-1367. |
| [9] | COUCLELIS H. Of Mice and Men: What Rodent Populations Can Teach Us About Complex Spatial Dynamics [J]. Environment and Planning A, 1988, 20: 99-109. |
| [10] | CHEN Jianping, DING Huoping, WANG Gongwen,et al. Desertification Evolution Modeling through the Integration of GIS and Cellular Automata [J]. Journal of Remote Sensing, 2004, 8(3): 254-260. (陈建平, 丁火平, 王功文,等. 基于GIS和元胞自动机的荒漠化预测模型[J]. 遥感学报, 2004, 8(3): 254-260.) |
| [11] | CLARKE K C, GAYDOS L. Loose-coupling a Cellular Automata Model and GIS:Long-term Urban Growth Prediction for San Francisco and Washington/Baltimore [J]. International Journal of Geographical Information Science, 1998,12(7): 699-714. |
| [12] | ZHANG Yihan, LI Xia, LIU Xiaoping, et al. The CA Model Based on Data Assimilation [J]. Journal of Remote Sensing, 2011, 15(3): 475-491. (张亦汉, 黎夏, 刘小平, 等. 基于数据同化的元胞自动机[J]. 遥感学报, 2011, 15(3): 475-491.) |
| [13] | REICHLE R H, MCLAUGHLIN D B, ENTEKHABI D. Hydrologic Data Assimilation with the Ensemble Kalman Filter [J]. Monthly Weather Review, 2002, 130(1): 103-114. |
| [14] | LI Xin, HUANG Chunlin, CHE Tao, et al. Development of a Chinese Land Data Assimilation System: Its Progress and Prospects [J]. Progress in Natural Science, 2007, 17(2): 163-173. (李新, 黄春林, 车涛, 等. 中国陆面数据同化系统研究的进展与前瞻[J]. 自然科学进展, 2007, 17(2): 163-173.) |
| [15] | LI Xin, BAI Yulong. A Bayesian Filter Framework for Sequential Data Assimilation [J]. Advance in Earth Science, 2010, 25: 515-522. (李新, 摆玉龙. 顺序数据同化的Bayes滤波框架[J]. 地球科学进展, 2010, 25: 515-522.) |
| [16] | EVENSEN G. Sequential Data Assimilation with a Nonlinear Quasigeostrophic Model Using Monte-Carlo Methods to Forecast Error Statistics [J]. Journal of Geophysical Research, 1994, 99(C5): 10143-10162. |
| [17] | AKSOY A, Mesoscale Ensemble-based Data Assimilation and Parameter Estimation [D]. Texas:Texas A&M University,2005. |
| [18] | MORADKHANI H, SOROOSHIAN S, GUPTA H V, et al. Dual State-parameter Estimation of Hydrological Models Using Ensemble Kalman Filter [J]. Advances in Water Resources, 2005, 28(2): 135-147. |
| [19] | TONG M J, XUE M. Simultaneous Estimation of Microphysical Parameters and Atmospheric State with Simulated Radar Data and Ensemble Square-root Kalman Filter.Part II: Parameter Estimation Experiments [J]. Monthly Weather Review, 2008(136): 1649-1668. |
| [20] | ZHENG D Q, LEUNG J K C, LEE B Y. Online Update of Model State and Parameters of a Monte Carlo Atmos-pheric Dispersion Model by Using Ensemble Kalman Filter [J]. Atmospheric Environment, 2009,43(12): 2005-2011. |
| [21] | WU F, WEBSTER C J. Simulation of Land Development through the Integration of Cellular Automata and Multicriteria Evaluation [J]. Environment and Planning B: Planning and Design, 1998, 25(1): 103-126. |
| [22] | CROW W T, WOOD E F. The Assimilation of Remotely Sensed Soil Brightness Temperature Imagery into a Land Surface Model Using Ensemble Kalman Filtering: A Case Study Based on ES-TAR Measurements during SGP97 [J]. Advance Water Resources, 2003, 26:137-149. |
| [23] | LIU Fang. Bayesian Time Series: Analysis Methods Using Simulation Based Computations[D]. Durham: Duke University, 2000. |