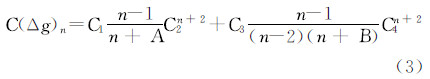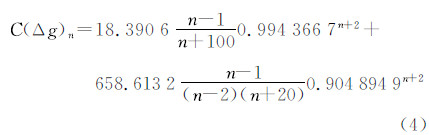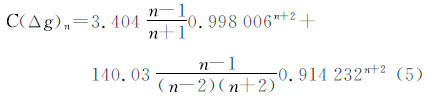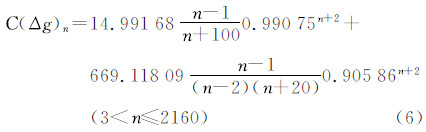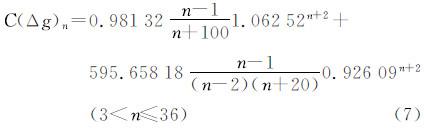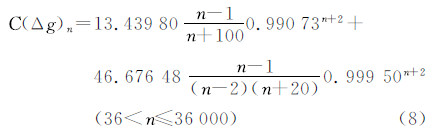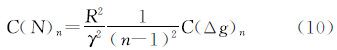2.西安测绘研究所,陕西西安 710054
2.Xi'an Institute of Surveying and Mapping,Xi'an 710054, China
1 引言
重力异常阶方差是地球重力场统计分析和描述扰动场元(如扰动重力、大地水准面高、垂线偏差等)的频谱特征(spectral sensitivity)的重要参考量,对于分析和认识地球重力场的特性及在相关领域的总体设计中都具有重要意义,如著名的Kaula准则即是对重力场位系数阶方差分析归纳得到的结果。此外,阶方差模型也是评估重力场模型截断误差的基本依据,在最小二乘配置和相关重力场误差分析中具有重要作用。经典的重力异常阶方差模型有Tscherning&Rapp模型、Jekeli模型、Rapp模型等[1, 2, 3] 。文献[4]利用Tscherning&Rapp模型计算了空中重力异常的代表误差并给出了空中重力测量的最佳高度;文献[5]利用Tscherning&Rapp模型计算区域重力大地水准面确定的相对精度;文献[6]利用重力异常阶方差模型分析海面高数据反演重力异常的精度指标;文献[7-8]利用Tscherning&Rapp的重力异常阶方差模型给出了大地水准面高、重力异常、扰动重力在不同频段(截止36000阶)的频谱特征分布。
阶方差模型的构建一般由相应的重力场模型计算的离散阶方差拟合得到(如Jekeli模型由GEM-9重力场模型数据拟合得到),文献[9]利用360阶DQM94A模型建立了基于指数函数形式的DVM96阶方差模型,并以此为基础计算了外空扰动引力场的传播特性,但DVM96模型在低频部分的精度不高。阶方差模型的准确性取决于模型的数学形式以及采用重力场模型的精度和分辨率。2008年,美国地理空间情报局(NGA)发布了最新的2159阶次地球重力场模型-EGM2008(可扩展至2190阶2159次)。国内外众多学者的研究表明,EGM2008模型表征重力场方面较之传统重力场模型有明显提高[10, 11, 12, 13, 14, 15]。为此,本文将以EGM2008模型为基础构建新的重力异常阶方差模型,并以此模型重新分析重力场扰动场元的频谱特征。
2 经典重力异常阶方差模型的分析比较
重力异常的阶方差在球近似下可用扰动位模型的位系数表示为
式中,n表示扰动位模型的阶数;C(Δg)n表示第n阶的重力异常阶方差;γ表示正常重力; 表示正常化的扰动位位系数。
表示正常化的扰动位位系数。
由于重力场模型阶数有限,因此只能通过构建阶方差模型计算更高阶的阶方差。文献[3]构建了经典的重力异常阶方差模型并拟合出模型中的常数[3],其形式为
莫里兹在总结前人研究基础上,提出了阶方差模型的通用表达形式[16]在式(3)中,共有C1、C2、C3、C4、A、B 6个参数,其中A、B两个参数为整数,C1、C3的单位为(10-5m/s2)2。该模型形式得到广泛认可和使用,学者Jekeli和Rapp的阶方差模型都采用了这种形式。
Jekeli模型为[2]
Rapp模型为[1]
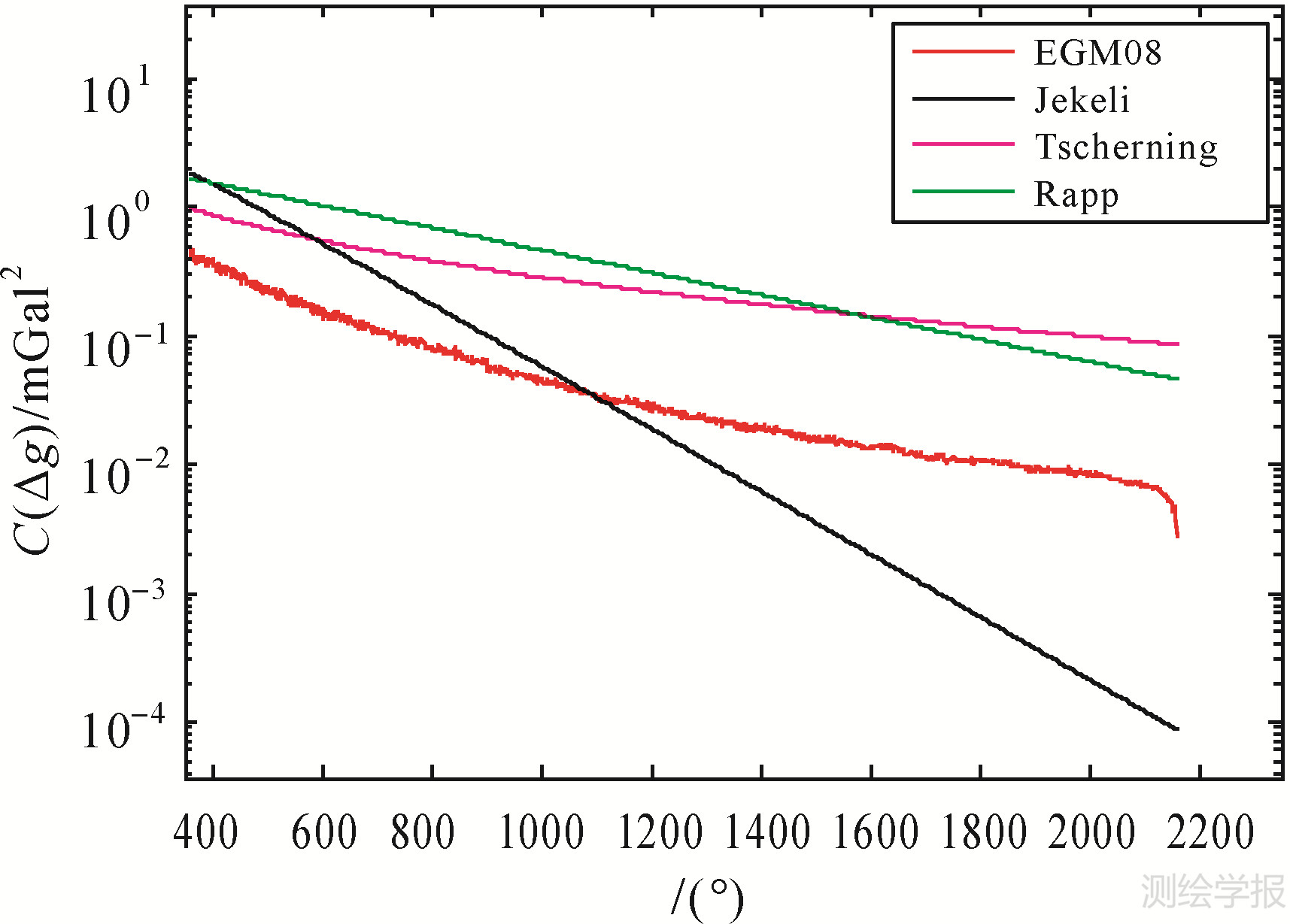
为了对经典重力异常阶方差模型(Tscherning&Rapp模型、Jekeli模型、Rapp模型)进行分析比较,将扰动场元的频谱划分为3个频段即3~36阶、37~360阶、361~2160阶。分别计算3个频段内的不同模型的阶方差值,同时利用EGM2008位模型按照式(1)计算直到2160阶的阶方差值,以EGM2008的计算值作为基准进行比较,比较后的统计结果见表 1,3种阶方差模型与EGM2008位模型获得的重力异常阶方差在不同频段的比较见图 1、图 2、图 3。
| (10-5m/s2)2 | |||||
| 阶方差
模型 |
统计值 | 3~
36阶 |
37~
360阶 |
361~
2160阶 |
3~
2160阶 |
| Tscherning | 均值 | 3.27 | 0.60 | 0.22 | 0.35 |
| 标准差 | 5.43 | 0.66 | 0.12 | 0.76 | |
| Jekeli | 均值 | 0.60 | 2.06 | 0.13 | 0.43 |
| 标准差 | 2.10 | 0.46 | 0.30 | 0.80 | |
| Rapp | 均值 | -0.30 | 0.60 | 0.38 | 0.40 |
| 标准差 | 2.52 | 0.63 | 0.34 | 0.51 | |

|
| 图 1 3种阶方差模型与EGM2008位模型在3~36阶的比较(1 mGal=10-5 m/s2) Fig. 1 Comparison between three classical models and EGM2008 model in 3~36 spectra |
|
| 图 2 3种阶方差模型与EGM2008位模型在37~360阶的比较 Fig. 2 Comparison between three classical models and EGM2008 model in 37~360 spectra |
|
| 图 3 3种阶方差模型与EGM2008位模型在361~2160阶的比较 Fig. 3 Comparison between three classical models and EGM2008 model in 361~2160 spectra |
从表 1和图 1、图 2、图 3可以看出,重力异常阶方差总体上呈现出随着阶数增加而逐渐减小的趋势。在3~36阶的重力场低频部分,Tscherning模型与Jekeli和Rapp模型相比,表现较差;在37~360阶的重力场中频部分,Jekeli模型与其他两个模型相比表现出较大的系统偏差,3种经典模型总体上在量级上都要高于EGM2008模型。在361~2160阶的扰动重力场的高频部分,Jekeli模型衰减的幅度最大,另外两种模型的表现较为接近,在数值量级上也较小,但考虑到这一频段阶方差本身的量级在10-3~10-2之间,因此总体上3种阶方差模型的表现都较差。综合以上分析,3种传统的阶方差模型由于限于当时的观测条件,其模型效果与EGM2008位模型的计算结果表现出较大的差异,因此这些模型已经不能准确地描述扰动场元在各个频段的频谱特征。 3 重力异常阶方差模型的构建
从前面的分析可看出,传统的阶方差模型的准确性不高,其主要原因应该是构建过程中采用的位模型准确度不高,因此有必要利用EGM2008模型的数据重新构建新的阶方差模型,以满足扰动场元高频特征计算的需要。
莫里兹提出的阶方差模型形式(见式(3))得到广泛认可和使用,因此本文将在此形式基础上构建更加符合地球重力场实际的高阶阶方差模型。为了得到模型中的6个参数,利用EGM2008模型计算的阶方差数据按照非线性最小二乘回归[17](95%置信区间)的方法进行拟合。考虑到阶方差模型的1阶为0,2阶无法直接求出,在实际拟合中利用3~2160阶的数据进行拟合。
实际拟合时发现很难同时拟合6个参数,因此首先固定A、B两个参数,而后利用3~2160阶的数据拟合剩余的4个参数,最后利用这些参数按照式(3)计算3~2160阶的阶方差并与EGM2008模型计算值进行比较,然后调整A、B两个参数值并重复以上过程直到得到最优值。表 2给出了A、B在不同取值(这里只列出部分数值)下模型参数的拟合值以及比较结果。
| A | B | C1/(10-5m/s2)2 | C 2 | C3/(10-5m/s2)2 | C4 | 差值均值 | 标准差 |
| 100 | 20 | 14.99168 | 0.99075 | 669.11809 | 0.90586 | -0.03 | 0.27 |
| 100 | 10 | 14.71037 | 0.99085 | 345.27135 | 0.92413 | -0.06 | 0.54 |
| 200 | 20 | 26.2152 | 0.98943 | 658.40664 | 0.90860 | 0.10 | 0.48 |
| 150 | 20 | 20.54518 | 0.98996 | 661.99587 | 0.90769 | 0.03 | 0.33 |
| 1 | 2 | 4.47572 | 0.99443 | 125.40079 | 0.92883 | -0.21 | 1.04 |
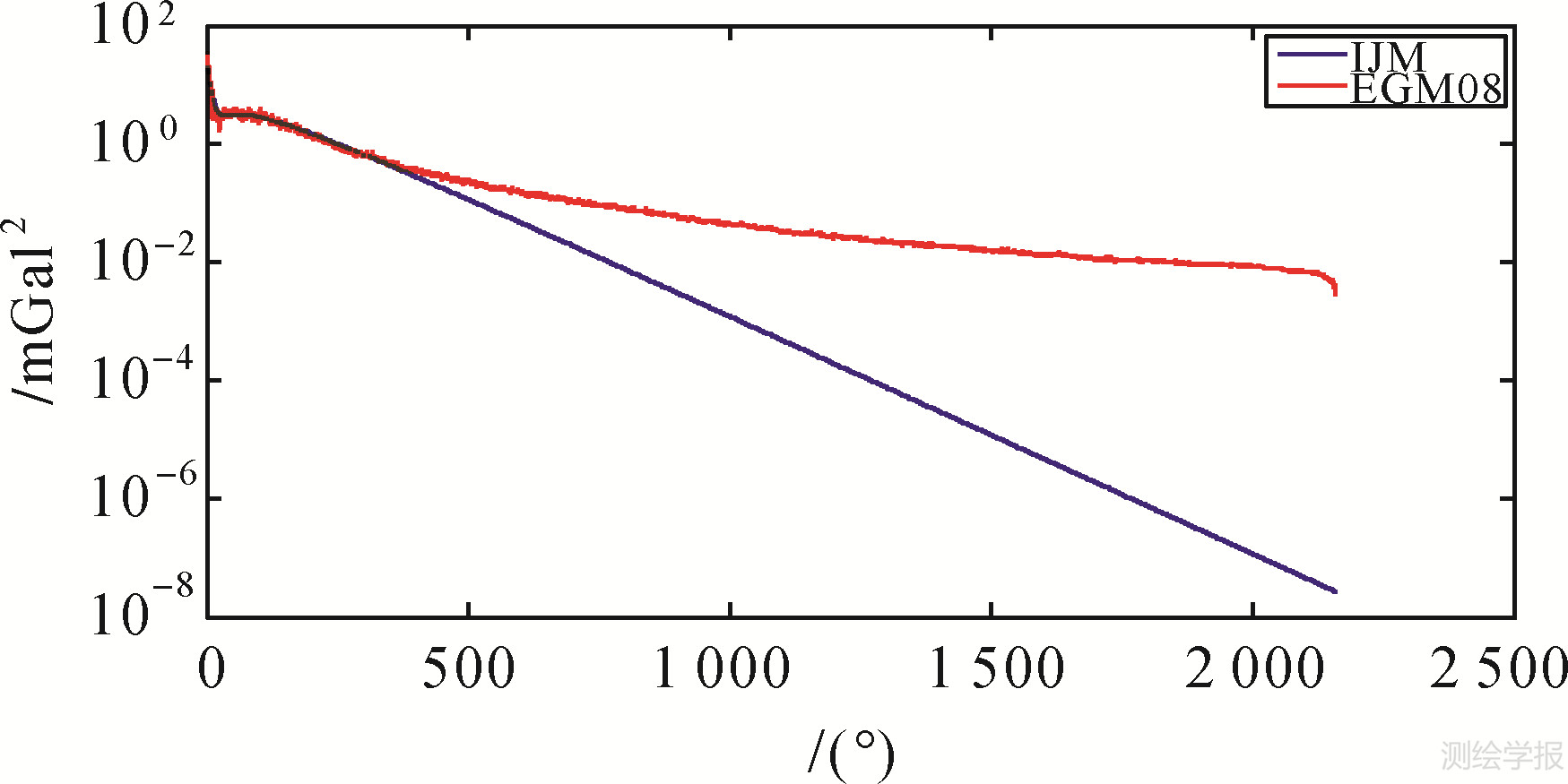
计算结果表明,在A、B取值分别为100、20时,阶方差模型与EGM2008模型一致性最强,为了体现对传统经典模型的继承性,本文选取Jekeli模型中A、B的值作为新模型的参数值,并将对应的C1、C2、C3、C4参数值作为新的阶方差模型的参数取值,此时新的阶方差模型(本文简称IJM模型,improved Jekeli model)表述如下,其曲线图见图 4。
|
| 图 4 IJM模型变化趋势图 Fig. 4 Map of IJM model |
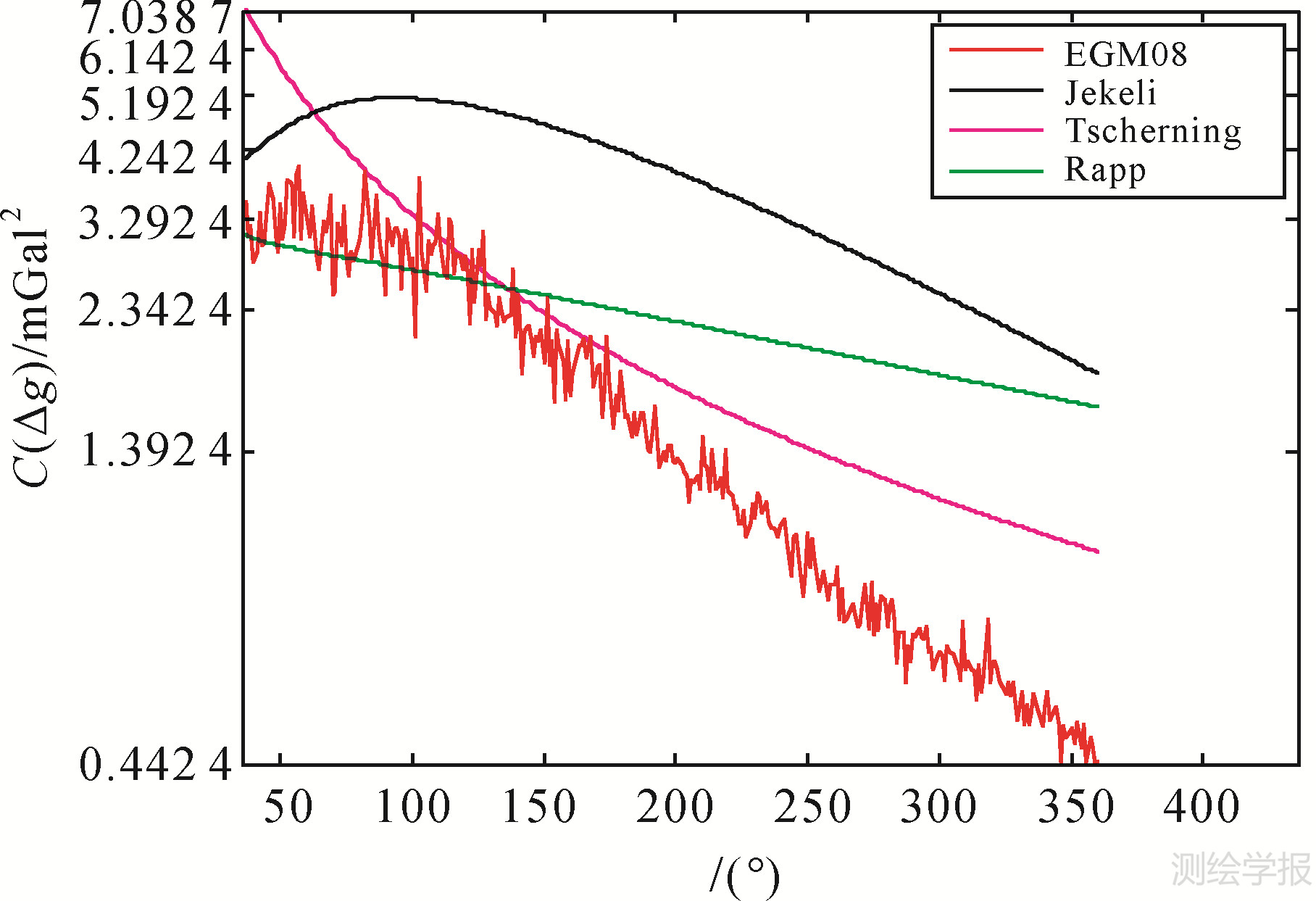
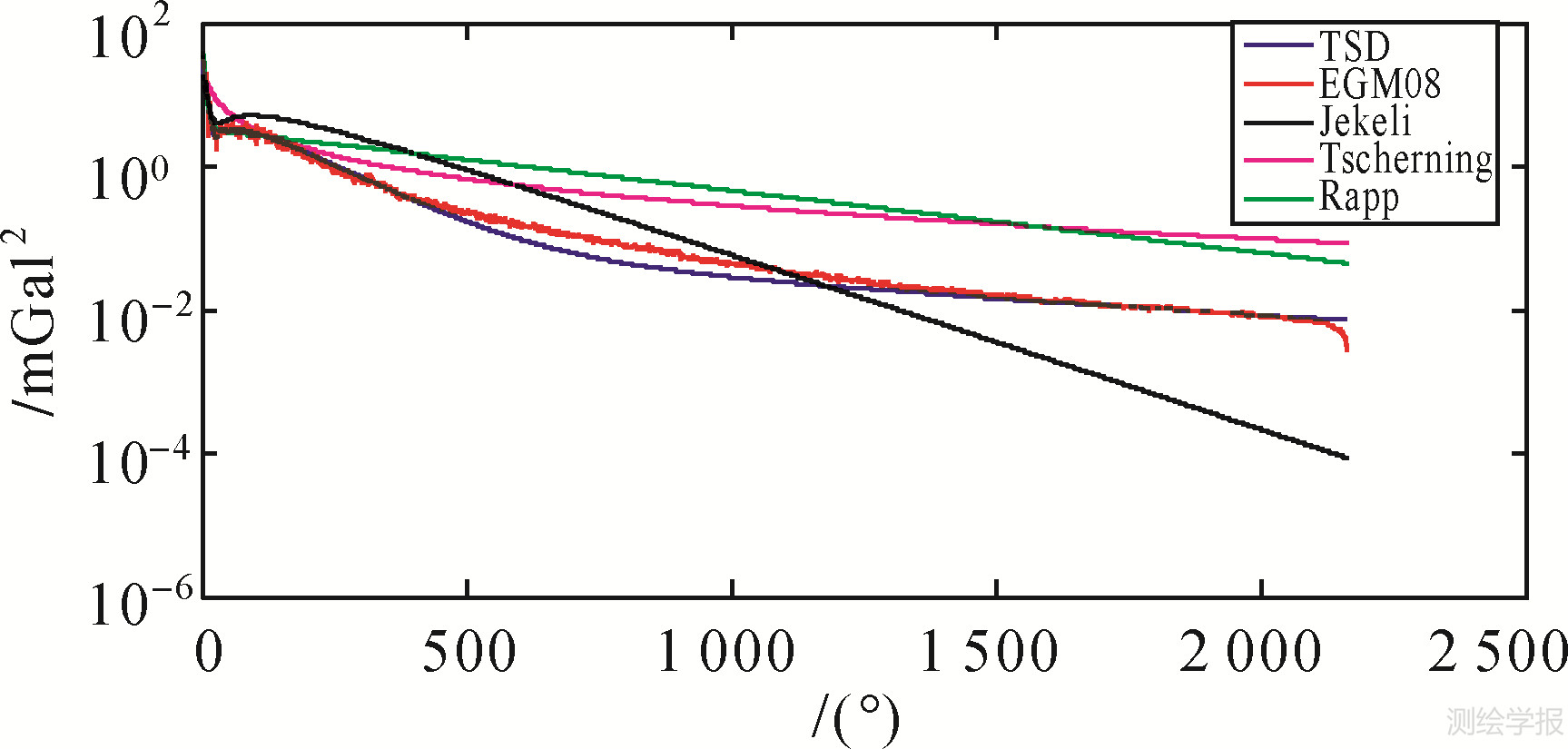
IJM阶方差模型虽然较之传统模型有较大改进,但从图 4可以看出从500阶以后,新阶方差模型的量级呈线性急剧衰减,这与EGM2008的变化明显不符。从图 1可以看出,前36阶的阶方差变化幅度很大,36阶以后的变化相对平缓,因此,若采用分段拟合的方法将阶方差模型分为3~36阶和37~2160阶分别拟合将更符合实际。拟合方法仍采用前面的非线性最小二乘回归,A、B的值仍取为100、20,重新拟合后的模型参数见表 3,本文将此阶方差模型简称为TSD模型(two spectral sector degree variance model),该模型表述见式(7)、式(8),TSD模型与其他阶方差模型的对比见图 5。
|
| 图 5 5种阶方差模型的变化曲线图 Fig. 5 Comparison of five degree variance models |
| 频段 | A | B | C1/(10-5m/s2)2 | C 2 | C3/(10-5m/s2)2 | C4 | 差值均值 | 标准差 |
| 3~36 | 100 | 20 | 0.98132 | 1.06252 | 595.65818 | 0.92609 | 0.00 | 0.25 |
| 37~2160 | 100 | 20 | 13.43980 | 0.99073 | 46.67648 | 0.99950 |
从表 3的比较结果可以看出,TSD模型总体上比其他阶方差模型要优异,从图 5也可以直观的看出,TSD模型的阶方差(图 5中蓝色线条)在变化趋势上更加符合EGM2008模型的变化趋势(图 5中红色线条)。 4 扰动场元频谱特征的计算
扰动场元在各频段的频谱特征可以用其在不同阶次之间的阶方差和来表示,其频谱特征就表现为各阶次间阶方差的比例。根据已有的频谱分布规律,本文将扰动场元的阶次划分为2~36阶、37~360阶、361~3600阶、3601~36000阶。所计算的扰动场元包括重力异常、大地水准面高、扰动重力、垂线偏差。在球近似下,大地水准面高、扰动重力、垂线偏差的阶方差都可以用重力异常的阶方差表示,具体如下:
扰动重力(径向)的阶方差为
大地水准面高的阶方差为
垂线偏差的阶方差为
实际计算中采用TSD阶方差模型,其中3~36阶用式(7)计算,37~36000阶用式(8)计算,计算中重力异常的2阶方差利用EGM2008模型获得,C(Δg)2=7.59×(10-5m/s2)2,最终获得的扰动场元的频谱特征见表 4。
| 不同频段分布 | ||||
| 扰动场元/阶 | 2~36 | 37~360 | 361~3600 | 3601~36000 |
| 大地
水准面高/(%) |
99.67 | 0.33 | 0.00 | 0.00 |
| 重力异常/(%) | 26.55 | 62.53 | 10.58 | 0.33 |
| 扰动重力/(%) | 43.82 | 48.05 | 7.88 | 0.25 |
| 垂线偏差/(%) | 39.25 | 51.91 | 8.58 | 0.26 |
文献[3]给出了基于Tscherning阶方差模型的扰动场元的频谱特征,见表 5。对比表 4和表 5的频谱分析结果可以看出,大地水准面高的频谱特性并没有太大的变化,其能量主要分布在360阶以下的低频部分;重力异常和扰动重力在360阶前的频谱比重有较大增加,2~36阶分别增加了4%和11%,37~360阶分别增加了21%和11%,两个扰动场元在360阶前的比重总体上增加了25%和22%,而360阶后的比重则相应的减少;垂线偏差的频谱分布较文献[16]中的结果也有明显的变化,在360阶以后占的比重大幅减小。扰动场元频谱敏感性的变化本质上反映了TSD模型与Tscherning模型的差异,TSD模型360阶以后的阶方差量级明显要小于Tscherning模型,这就造成了360阶以后的频谱特性必然有较大的改变。总体而言,利用TSD阶方差模型获得的扰动场元频谱分布较之传统分析结果有较大的变化,其中重力异常、扰动重力及垂线偏差在中、低频部分的能量有明显的增加而高频及甚高频部分的比重有明显的减少。
| 不同频段分布 | ||||
| 扰动场元/阶 | 2~36 | 37~360 | 361~3600 | 3601~36000 |
| 大地
水准面高/(%) |
99.2 | 0.8 | 0.00 | 0.00 |
| 重力异常/(%) | 22.5 | 41.9 | 32.7 | 2.8 |
| 扰动重力/(%) | 32.2 | 37.3 | 28.1 | 2.4 |
利用最新的全球引力位模型-EGM2008对Tscherning、Jekeli、Rapp 3种经典的重力异常阶方差模型进行了分析比较,3种模型的标准差分别为0.76×(10-5m/s2)2、0.80×(10-5m/s2)2和0.51×(10-5m/s2)2,总体上3种模型的量级要高于EGM2008的量级。比较结果表明这些模型已经不能准确地描述扰动场元在各个频段的频谱特征。
利用EGM2008位模型计算的阶方差按照非线性最小二乘回归的方法重新构建了分段的重力异常阶方差模型即TSD模型,TSD模型在3~2160阶的频段上与EGM2008位模型有较强的一致性,其标准差为0.25×(10-5m/s2)2。
在TSD模型基础上计算了不同频段内大地水准面高、重力异常、扰动重力、垂线偏差4个扰动场元的频谱特征。计算结果表明:扰动场元频谱分布较之传统分析结果有较大的变化,其中重力异常、扰动重力及垂线偏差在中、低频部分的能量有明显的增加而高频及甚高频部分的比重有明显的减少。如果这种变化能够反映地球重力场的实际,则意味着如果通过卫星重力测量手段可以恢复至360阶的重力场,则可以获取比传统认识中更多的重力场信息。
为了进一步验证本文构建的重力异常阶方差模型,可以在频域计算地面或空中的重力异常代表误差,而后利用实际的地面或空中重力数据计算真实的代表误差,两者进行比较分析。重力异常阶方差模型在最小二乘配置理论及应用中具有重要意义和作用,如在卫星重力径向梯度数据的调和分析中应用重力异常阶方差推导扰动引力位系数与扰动引力梯度之间的协方差关系[18]等。未来,将在以上方面对本文构建的TSD模型进行更加深入的研究和分析。
| [1] | RAPP R. Potential Coefficient and Anomaly Degree Variance Modelling Revisited[R]. Columbus: Ohio State University, 1979. |
| [2] | JEKELI C. An Investigation of Two Models for the Degree Variances of Global Covariance Functions[R]. Columbus: Ohio State University, 1978. |
| [3] | TSCHERNING C C, RAPP R. Closed Covariance Expressions for Gravity Anomalies, Geoid Undulations, and Deflections of the Vertical Implied by Anomaly Degree Variance Models[R]. Columbus: Ohio State University, 1974. |
| [4] | SHI Pan, WANG Xingtao. Frequence Domain Analysis for the Determination of Terrestrial Land Mean Gravity Anomaly from Airborne Gravimetry[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(4): 301-308. (石磐, 王兴涛. 空中测量地面平均重力异常的频域分析[J]. 测绘学报, 1995, 24(4): 301-308.) |
| [5] | XU Xi, ZHU Jianjun. Relative Accuracy Estimation for Determining Regional Gravimetric Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 384-387. (许曦, 朱建军. 区域重力大地水准面确定的相对精度估计[J]. 测绘学报, 2009, 38(5): 384-387.) |
| [6] | ZHAI Zhenhe, SUN Zhongmiao. Spherical Harmonic Analysis of the Error Propagation between Mean Gravity Anomaly and Sea Surface Height Data[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 137-140. (翟振和, 孙中苗. 海面高数据与平均重力异常误差传播的球谐分析[J].大地测量与地球动力学, 2010, 30(2): 137-140.) |
| [7] | SCHWARZ K P. Data Types and Their Spectral Properties[C]//Proceedings of the Beijing International Summer School on Local Gravity Field Approximation. Beijing:[s.n.], 1984: 1-66. |
| [8] | MICHAEL K. An Analysis of the Combination and Downward Continuation of Satellite, Airborne and Terrestrial Gravity Data[D]. Calgary: University of Calgary, 2003. |
| [9] | XIA Zheren, SHENG Zongqi, LI Yingchun. Propagation Properties of Disturbing Gravity Field outside the Earth[J]. Acta Geophysica Sinica, 1998, 41(4): 484-487. (夏哲仁, 盛宗琪, 李迎春. 外空扰动引力场的传播特性[J]. 地球物理学报, 1998, 41(4): 484-487.) |
| [10] | PAVLIS N K, HOLMES S A. KENYON S C. An Earth Gravitational Model to Degree 2160: EGM2008[R]. Vienna: 2008 General Assembly of the European Geosciences Union. 2008. |
| [11] | KIAMEHR R. Evaluation of the New Earth Gravitational Model EGM2008 in Iran[J]. Geophysical Research, 2009, 1(11): 16-19. |
| [12] | HIRT C, MARTI U, BVRKI B, et al. Assessment of EGM2008 in Europe Using Accurate Astrogeodetic Vertical Deflections and Omission Error Estimates from SRTM/DTM2006.0 Residual Terrain Model Data[J]. Journal of Geophysical Research, 2009, 115(10404): 1-13. |
| [13] | ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM2008 and It’s Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-287. (章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. )测绘学报, 2009, 38(4): 283-287. |
| [14] | RONG Min, ZHOU Wei, CHEN Chunwang. Comparison between EGM2008 and EGM96 Model in Chinese Area[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 123-126. (荣敏, 周巍, 陈春旺. 重力场模型EGM2008和EGM96在中国地区的比较与评价[J]. 大地测量与地球动力学, 2009, 29(6): 123-126.) |
| [15] | LIU Xiaogang, WU Xiaoping, ZHAO Dongming, et al. Comparison between Trajectory Disturbing Gravity Calculated with Earth Gravity Field Models of EGM96 and EGM2008[J]. Journal of Geodesy and Geodynamics, 2009, 29(5): 62-65. (刘晓刚, 吴晓平, 赵东明, 等. EGM96和EGM2008地球重力场模型计算弹道扰动引力的比较[J]. 大地测量与地球动力学, 2009, 29(5): 62-65.) |
| [16] | LU Zhonglian. Theory and Method of Earth Gravity Field[M]. Beijing: Liberation Army Publishing House, 1996. (陆仲连. 地球重力场理论与方法[M]. 北京: 解放军出版社, 1996.) |
| [17] | WANG Zhenglin, GONG Chun, HE Qian. Mastery of Scientific Computation of MATLAB[M]. Beijing: Publishing House of Electronics Industry, 2007. (王正林, 龚纯, 何倩. 精通MATLAB科学计算[M]. 北京: 电子工业出版社, 2007.) |
| [18] | WU Xing, ZHANG Chuanding, LIU Xiaogang. Least-square Collocation Harmonic Analysis of the Radial Satellite Gravity Gradients[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 472-475. (吴星, 张传定, 刘晓刚. 卫星重力径向梯度数据的最小二乘配置调和分析[J]. 测绘学报, 2010, 39(5): 472-475.) |