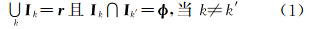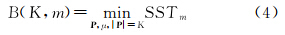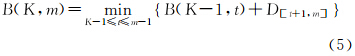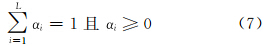2. 东华理工大学 测绘工程学院,江西 抚州 344000
2.School of Geomatics, East China Institute of Technology,Fuzhou 344000, China
1 引 言
线性混合模型建立在光谱线性可加性的基础上,具有模型简单、物理含义明确和普适性强等优点[1]。借助于线性混合光谱模型,人们能够从像元的表观光谱特性,分离和提取各像元组分的光谱,从而反演地物组分的含量。针对混合光谱模型,研究人员已从线性模型的理论[2]、端元光谱自动获取[3, 4]、算法模型[5, 6, 7]、空间信息有效利用[8]以及可视化分解结果[9]等方面都有比较深入的研究。有关研究与试验分析表明一个有效地提高混合像元分解精度的关键点在于改善端元光谱矩阵的结构[2]。
设S=[s1s2…sk]是大小为m×k的端元光谱矩阵,文献[2]表明混合像元的分解精度与S的结构Tr[(STS)-1]正相关。由于S矩阵的各列元素表示对应地物端元的光谱值,则提取影像中的最优端元光谱si(i=1,…,k),使得端元光谱之间的差距最大[3, 4],就意味着找出S的最佳结构。另一方面,由于S矩阵的各行元素表示为端元光谱对应波段值,则如果通过光谱提取与选择技术能够减小各地物光谱波段之间的相关性,或者增加不同地物光谱之间的可分性,就意味着改善了S的结构。文献[10]提出一种利用微分光谱特征进行混合像元分解的方法,结果表明只要端元光谱能够保持地物的诊断性光谱特征,就能够取得满意的分解结果。文献[11]提出利用光谱矢量多分辨的高频与低频系数特征进行混合像元分析,结果表明在计算效率和分解精度上都得到显著提高。由于小波变换在时、频两域都具有表征信号局部特征的能力,能够精细地描述光谱的波峰与波谷等曲线特性,提取的光谱特征具备减小同类地物光谱变化,同时增加不同地物光谱的可分性的能力,非常适合改善端元光谱矩阵的结构[11]。然而,小波变换是基于基函数展开的,各个尺度上的小波函数都是通过基函数的尺度和平移变换获得,每分解一次光谱信号,则逼近信号和细节的长度都减小一半,使得在不同尺度上得到的逼近信号特征之间存在差异[12]。因此,光谱维小波特征可能有两方面不足:① 以固定的基函数导出的小波函数难以在不同尺度上准确地逼近局部信号特征;② 由于光谱特征数随小波分解的层数成指数减少,因此通过原始光谱只能提取少数几个尺度下的光谱特征。
本文直接在影像光谱的段内离差平方和最小化准则下,提出一种高光谱影像光谱多尺度光谱分割的特征提取方法,以提高混合像元分解的分解精度。
2 基于多尺度光谱特征的分解 2.1 光谱最优K段分割假设由N个样本组成的高光谱像元集合为R={rij|1≤i≤N,1≤j≤M},其中rij为第i像元第j波段的像元值,M为波段数。光谱最优K段分割就是在以段内均值表达段内光谱时,找出K个分割点P={p1,p2,…,pK},使得各段内离差平方和最小,而段间离差平方和最大。由K个分割点,可以把高光谱影像的光谱分割成k段连续区间Ik=[pk,pk+1),显然有
式中,φ为空集,这表明Ik完整地无缝地分割整个光谱。由于在模型中每个像元用各自分割区间的平均值替代,则所有样本光谱的段内离差平方和累加为
式中,μik是各像元在分割区间Ik内的平均值,记|Ik|为第k区间段中波段数目,则
对于固定的像元集合R,像元的段内与段间总离差平方和是固定的。因此段内离差平方和最小,则意味着段间离差平方和最大。因此,光谱k段最优分割转化为确定Ik,使式(2)最小,这通常采用动态规划技术来优化Ik[13]。为此定义一个计算过程函数
式中,SSTm表示式(2)中只考虑前m个光谱;|P|=K表示使用K个分割点。由于对1<K≤m≤M有B(K,m)随着K增大而减小,因此定义递推关系
式中
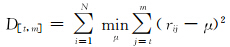
主要计算步骤如下:
步骤1 对1≤m≤M,令B(1,m)=D[1,m];
步骤2 对所有K,1<K≤m≤M利用式(5)求出rK,n*,使得B(K,m)最小;
步骤3 重复步骤2,直到找到全部的分割点B(K,M),B(K-1,rK,n*),…
该算法的复杂度为O(NM3),但由于高光谱传感器光谱波段数目M一般远小于影像像元数目(或样本数目)N,因而内循环计算速度较快,计算效率可以接受。如果N比较大,为提高计算效率,实际应用中可以采用以下两种方法:① 对影像(或样本)进行k均值聚类,并选取聚类中心的光谱进行多尺度分析,获取相应的分割点。但为了使聚类中心的光谱能够较好地代表影像的光谱情况,聚类数目一般设置较大;② 设定一个阈值θ,并对影像(或样本)进行光谱相似性分析,并且只保留那些光谱相似性小于θ的样本参与光谱多尺度分析。
2.2 多尺度特征提取与分析获取到最优分割点P后,利用式(3)求出平均值作为相应分割区间的特征值。如果使用不同的光谱分割数目,则可以提取不同尺度下的光谱特征。多尺度特征可以通过多尺度特征分析,选取最佳尺度特征或者不同分割尺度下的光谱特征组合进行混合像元的分解。为了计算方便,本文采用优选的尺度分割特征来进行混合像元分解。不难发现光谱最优K段分割实际上表示了原始光谱与某对角矩阵A=diag(A1,A2,…,AK)的乘积,其中Ai矩阵维数大小为|Ik|,且各元素相等。这表明该算法等价于在各分割段内光谱做均值滤波,且滤波器长度和数值只与各分割区间波段数相关。因此,光谱最优K段分割特征具有以下四个特点:① 光谱特征是由原始光谱经过线性变换得到的,保证了线性混合像元模型中光谱线性可加性的假设性前提;② 由于光谱分割的区间是由数据本身在离差平方和最小准则下自动确定的,分割的结果应该是光谱变化比较明显时分割区间相对较小,而在光谱曲线变化平缓的区间相对较大;③ 能够消除光谱噪声以及受环境变动等因素造成的光谱变动;④ 光谱分割区间数目根据需要确定,可以提取足够的多尺度光谱特征(只要不大于原始光谱波段)。
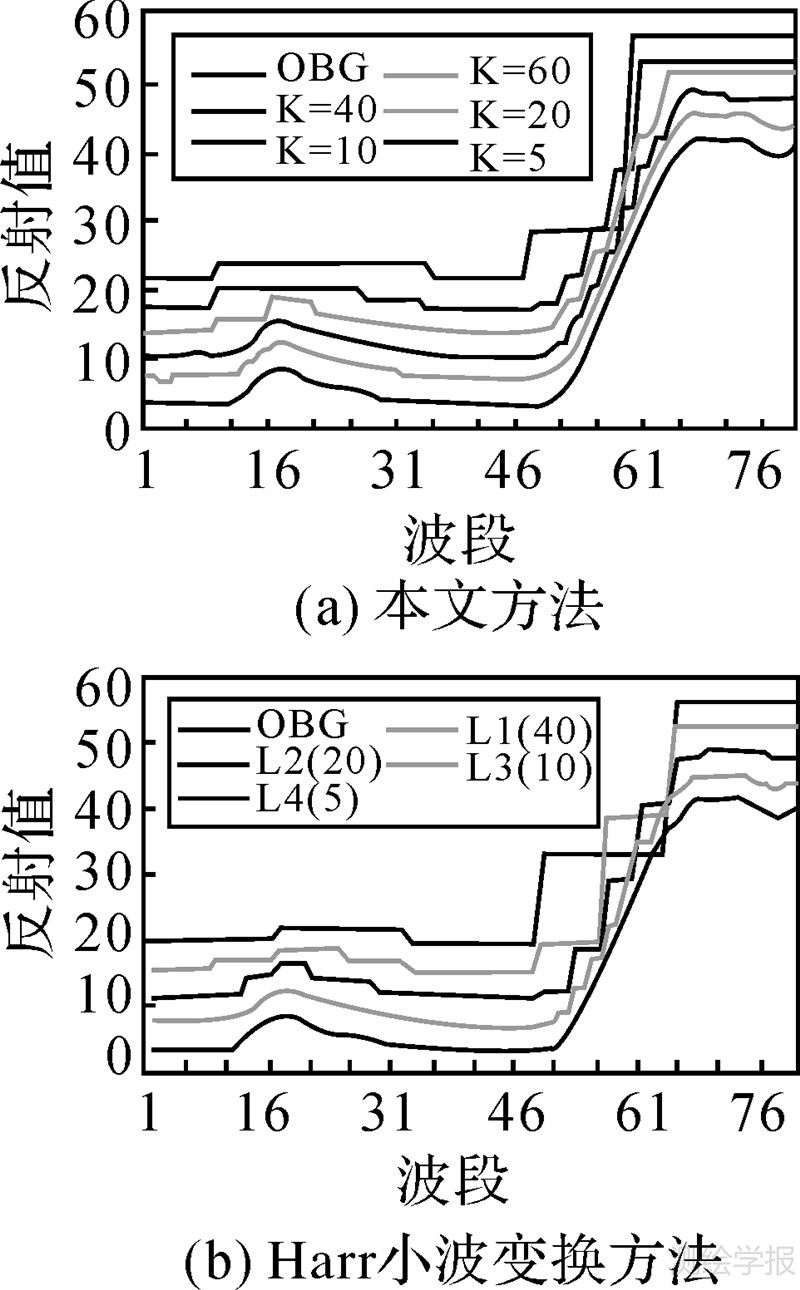
图 1为一条80波段的PHI影像的植被光谱多尺度分割的情况。其中图 1(a)为采用本文方法分割的结果;图 1(b)为Harr小波低频系数重建的结果。图 1(a)中最下面显示的曲线为原始的影像光谱,其他曲线从下往上分别为分割数等于60、40、20、10和5时的光谱情况。图 1(b)从下往上分别为Harr小波分解分别经过0、1、2、3和4层时用低频系数重建光谱的情况。由于小波进行0、1、2、3和4层Harr小波分解时的低频系数(即特征)个数刚好分别为80、40、20、10、5,可以直接比较图 1(a)与图 1(b)的结果。为了清楚地显示出光谱多尺度的分割效果,图 1(a)、图 1(b)中的光谱特征曲线在垂直方向(反射率)上都做了一定程度的位移。
|
| 图 1 光谱多尺度分割比较 Fig. 1 Comparison of multi-scale spectral segments |
从图 1(a)与图 1(b)中可以看出,随着分割数目的变化,特征光谱曲线在不同程度上逼近原始光谱,但仍然保持了原始光谱的基本形状。由于植被光谱在红光与近红外波段区域具有重要的变化,因此比较图 1(a)与图 1(b)在第50到第65波段(波长范围为690nm~746.4nm)的情况。从图中看出,两者在该区间都有比其他区域更精细的逼近,能够刻画出光谱的主要特征。但图 1(a)比图 1(b)在该区域具有更多的分割点,譬如在10个特征时,图 1(a)中有4个分割点,而图 1(b)中只有2个中分割点。这表明与Harr小波提取的特征相比,本文方法提取的光谱特征能够在光谱变化比较明显的区域有更为细致的表达。
2.3 线性混合模型在提取了光谱特征矢量后,采用限制性线性混合模型来估计像元的组分值
式(6)中,r为混合像元在K个特征光谱所组成的K个矢量,r是K行L列的矩阵,表示L个像元组份光谱特征矢量;α是像元组份比;ε0为K维误差项。式(7)是组份非负和总和为一的约束条件。利用式(6),用最小二乘法估计容易求出αLS=(STS)-1STr,但由于满足式(7)的解不存在解析解,一般寻求数值解法[14]。
记
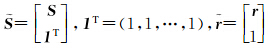
引入一个L维矢量λ=[λ1λ2…λL],由拉格朗日乘数法方程对变量求偏微分,可以导出两个迭代方程
式中,λ=(λ1,λ2,…,λL)为格朗日乘数。由式(8)、式(9)两式可以得出αCLS。采用活动函数集的方法[14]迭代求解出αCLS时,λ值满足凸优化理论的KT条件[14],从而能够保证αCLS为最优估计。
3 试验分析与讨论为了验证本文提出的方法,利用模拟的数据与真实的数据分别来进行试验分析。采用模拟数据的优点是完全知道构成混合光谱的真实组分,因而组分估计的结果能够直接反映算法本身的优劣。真实数据能够更好地反映算法在实际影像处理中的有效性,但获取真实数据的组分通常比较困难,所以不同方法的组分估计结果容易受其他因素影响。本文采用均方根误差和双变量统计函数(BDF)来评价试验结果。均方根误差直接反映混合像元的组分估计值与真实值之间的总体差异。BDF函数实质是一种散点图方式的方法,它用平面的横坐标表示估计值,纵坐标表示真实值,因此可以清楚地表明每个像元和每种地物的分解精度。
3.1 模拟数据试验分析图 2是从推扫式机载成像光谱PHI影像中选取的80波段的4种端元光谱,分别为道路、水体、水稻和菜地。考虑到遥感影像中广泛存在的“同物异谱”现象,因此,每种地物都选择了15条“同物异谱”的光谱来表达地物端元光谱的,以期生成“多端元光谱混合”的模拟光谱。模拟数据的生成方法如下:首先从每种地物的15条光谱中随机选择一条光谱为该地物的端元si,再产生一组[0, 1]内随机数τ=[τ1τ2τ3τ4]T,并且使得τ1+τ2+τ3+τ4=1,则混合光谱为r=s1·τ1+s2·τ2+s3·τ3+s4·τ4,最后在混合光谱r上附加信噪比为15∶1的高斯噪声,形成最终混合光谱。本试验一共生成了2100个混合光谱。并用限制性的分解方法分别计算了未经特征提取(ORG),基于Harr小波特征(HWT)以及本文方法(SMS)的分解结果。

|
| 图 2 模拟数据的4类端元光谱 Fig. 2 Four end-member spectra for simulating dataset |
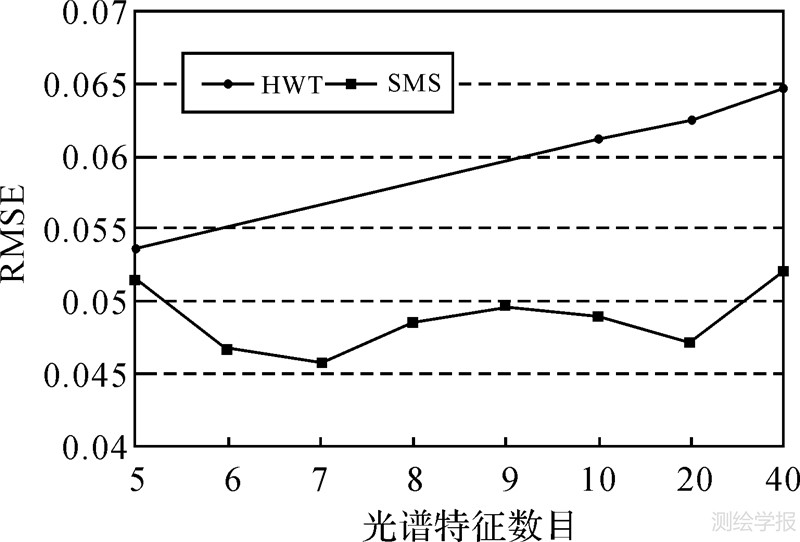
利用HWT和SMS方法提取多尺度光谱特征时,存在最佳小波分解层数或最佳分割数目问题。本试验中分别计算在不同光谱特征数目时真实值与估计值之间的平均平方根误差(RMSE),并选取RMSE最小时对应的特征数为最佳特征数目。由于小波变换只能进行1、2、3和4层分解,对应的特征数目为40、20、10、5。SMS方法也相应地选取40、20、10、5这几个特征,另外也对9、8、7、6个特征进行分析。光谱特征数目与分解组分的RMSE结果如图 3所示。
|
| 图 3 光谱特征数目与混合像元分解精度关系 Fig. 3 The relationships between RMSE and the number of spectral features |
从图 3可以看出HWT方法提取的特征数目按照2的倍数减小,因此不能提取出介于5~10之间的特征数目,而SMS方法提取任意数目的光谱特征。HWT在5个特征时取得最好结果,这时的RMSE为0.0536,而SMS方法在7个特征时取得最好结果,RMSE为0.0457。从图 3还可以得出在选取相同数目的光谱特征时,SMS的分解结果总是优于HWT方法。这表明本文提出的SMS方法较HWT方法在分解精度与特征数目选取方面都具有较大的优势。
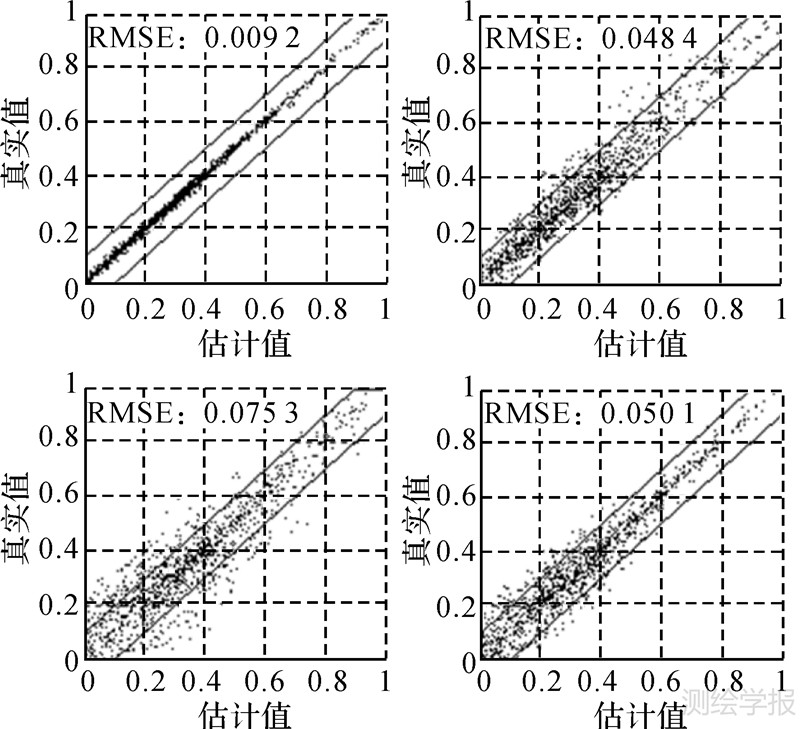
表 1列出了使用模拟数据分解误差的对照表情况,表中各方法后面的括号中表示了分解时使用的特征波段数目。从表 1可以得出,使用SMS特征分解的精度最高,其道路,水体,水稻和菜地估计值与真实值的RMSE分别为0.0092、0.048、0.0753、0.0501。SMS模型较ORG的分解精度大约有41%的提高,较HWT方法也有10%的提高。因此,模拟数据试验证实本文的方法能够显著地提高混合像元的分解精度。
| 使用方法 | 道路 | 水体 | 水稻 | 菜地 | 平均 | 提高率 |
| ORG(80) | 0.0174 | 0.0744 | 0.1338 | 0.0849 | 0.0776 | — |
| HWT(5) | 0.011 | 0.0549 | 0.0904 | 0.0583 | 0.0536 | 30.9% |
| SMS(7) | 0.0092 | 0.0484 | 0.0753 | 0.0501 | 0.0457 | 41.1% |
图 4为所绘制为SMS方法计算的估计值与真实值的BDF图,各图的左上角统计出了对应地物的均方根误差。图 4中上下两条平行直线是给定的10%分解误差边界。它的含义是落在两条平行线之间的点数越多,则分解的效果越好。从图 4看出这4种地物的组分估计值与真实值差别很小,表现在图中大部分的散点都落在10%的范围内,并且散点沿y=x的直线对称分布。
|
| 图 4 模拟数据分解结果的BDF评价 Fig. 4 Accuracy assessment with BDF for simulated data |
真实数据为福建省平和县境内的一幅大小为75×75像素的Hyperion遥感影像数据,该影像获取时间为2005-11月。通过对Hyperion数据预处理后,选取了可见光/近红外的40个波段进行试验分析。
验证数据选择同一区域大小为900像素×900像素的Alos高空间分辨影像。Alos影像获取时间为2006-12-20日,影像获取季节与Hyperion相同。由于Alos影像的空间分辨率为2.5m,远高于Hyperion影像30m的空间分辨率精度,并且这两幅影像空间分辨率刚好相差12倍,因此假设Alos影像中不存在混合像元,则Alos影像的分类结果可以折算为Hyperion影像相应地物的组分比。
为了保证Alos较高的分类精度,本试验采用面向对象分类技术进行分类,并对最后分类结果进行部分人工修改。这样把Alos影像分为以下几种主要地物类型,分别为水体、道路、果树、森林、农田、建筑物1、建筑物2、空地。分类结果经统计分析,分类结果的Kappa系数为0.88。由于部分地物类别的光谱在Hyperion上表现相似特性,试验中对部分地物进行了调整和组合,把道路、建筑物1、建筑物2定义为不透水面,森林/果园合并,这样获取了5种典型地物的分类结果,如图 5所示。利用一个大小为12×12的活动窗口在分类图中不重叠地滑动,并统计出窗口内各地物类别的百分含量,视为各地物在Hyperion影像中的真实组分值,用来评价各种方法在Hyperion影像混合像元分解精度。
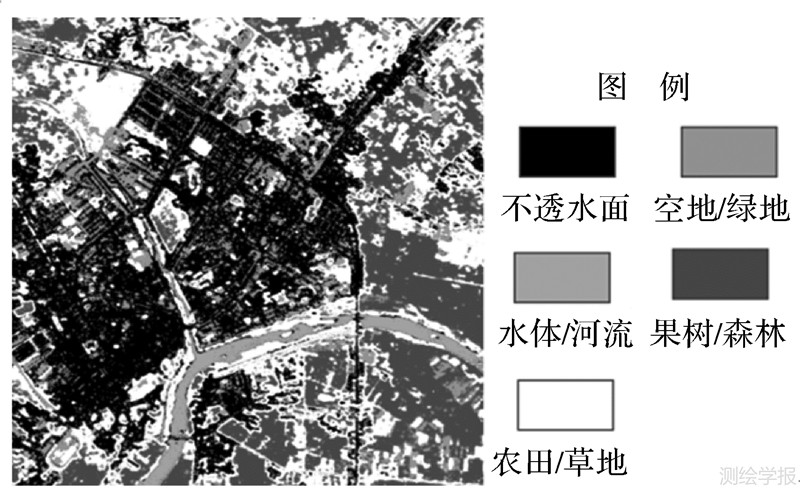
|
| 图 5 Alos影像的分类图 Fig. 5 Classification map of Alos image |
采用类似模拟数据的试探方法,可以确定出SMS与HWT方法的最佳光谱特征数目分别为12和10。提取出SMS和HWT方法相应数目的光谱特征后,再以限制性分解方法计算出各地物的真实值与估计值之间的RMSE结果如表 2所示。从表 2可以看出,SMS仍然取得最好的分解结果,其中不透水面、空地、水体、森林/果园、草地/农田的RMSE分别为0.2065、0.1608、0.1461、0.1867、0.2181。SMS方法较原始波段分解提高了约2.7%,相对HWT提高了2.2%。利用HWT方法取10个特征时,分解的结果最好,但只较原始波段分解精度提高0.5%。
| 使用 方法 | 不透 水面 | 空地 | 水体 | 农田/ 草地 | 森林/ 果园 | 平均 | 提高率 |
| ORG(80) | 0.2144 | 0.1655 | 0.1550 | 0.1897 | 0.2207 | 0.1887 | — |
| HWT(10) | 0.2127 | 0.1622 | 0.1570 | 0.1869 | 0.2203 | 0.1878 | 0.5% |
| SMS(12) | 0.2065 | 0.1609 | 0.1461 | 0.1867 | 0.2181 | 0.1837 | 2.7% |
为了检验SMS方法是否显著地改进了HWT方法的分解效果,引入McNamara测试标准[15],以确定两个模型之间的差异是否显著。设f12表示模型1计算正确而模型2计算不正确的数目,而f21为利用模型1计算不正确而模型2计算正确的数目,则McNamara统计为
式(10)的意义是如果Z12为负值,则表明模型1具有比模型2更高的精度。特别地,如果还有|Z12|>1.96,则表明模型1在α=0.05置信水平下精度显著高于模型2。
由于混合像元组分的估计值是[0, 1]区间的连续值,而McNamara测试统计的变量是由0-1损失函数定义的离散值,即正确时取值为1,错误时取值为0。因此,需要给出一个模型优于另一个模型的判别规则。由于大部分像元的估计值与真实值的都落在40%的范围内,因此,采用如下规则:如果模型1的组分估计值与真实值之间的RMSE度小于0.4,并且大于模型2的估计值与阈值T之和,则说明模型2的估计值更为“正确”,f21=1。否则,如果模型2的组分估计值与真实值之间的RMSE度小于0.4,并且大于模型1的估计值与阈值T之和,则f12=1。这个规则的合理性在于:① 它首先保证了两个模型的估计值与真实值在可接受的范围内(如0.4),超出该范围则认为它们都是错误的估计;② 为了说明像元估计值优劣不是由于随机因素影响,而是模型本身导致的,则需要保证此模型的估计值优于彼模型的估计值大于一定阈值T。
表 3是阈值T取不同值情况下McNamara统计的结果,从中可以看出SMS算法相对于ORG与HWT的McNamara值均小于-1.96,这表明在α=0.05置信水平下,本文提出的方法对于真实的数据也能够显著地改善混合像元的分解精度。
| T | 0.05 | 0.1 | 0.15 |
| SMS-HWT | -3.27 | -2.59 | -1.97 |
| SMS-ORG | -3.33 | -2.74 | -2.01 |
图 6是SMS方法分解结果的组分影像及误差影像情况。对照图 5的分类与图 6中的各组分影像,发现各地物的空间分布类似,并且在误差影像中没有发现明显的地物结构信息,这表明混合像元分解结果比较合理。但误差影像中存在大量亮斑点,说明组分估计值与真实值之间存在较大误差,这与表 2中各地物的分解误差较大是一致的。相对于模拟数据,真实数据分解结果的误差较大的原因可能是因为① Hyperion与Alos不同传感器的影响以及影像之间存在一定的配准误差;② 试验地区地物比较复杂,Alos影像分类精度影响了Hyperion试验的分解精度;③ Hyperion与Alos影像存在一定的时相差别,以及同类地物之间光谱差别大等的原因。

|
| 图 6 Hyperion影像的分解结果 Fig. 6 Unmixing results of Hyperion image |
为了可视化评价SMS方法的混合像元分解结果,进一步采用双变量分布统计(BDF)评价方法描述真实组分与估计组分间的关系。图 7为所绘制的SMS的BDF图,各图的左上角统计出了对应地物的均方根误差。从图 7看出这5种地物大部分的点都落在40%的范围内,并且散点基本沿y=x的直线对称分布。
3.3 模型的讨论与改进试验结果表明基于SMS与HWT特征的分解方法在处理模拟数据时的效果都要明显优于真实数据,其中重要的原因在于①模拟数据强调了混合光谱的“同物异谱”现象,即模拟的数据是由“多端元光谱”混合而成,具有较大的端元光谱内部变化;② 模拟数据信噪比为15∶1,而真实影像的信噪比通常为100∶1以上[16]。这表明基于光谱特征的混合像元分解方法特别适合于“光谱多端元混合”以及噪声较大的情况。这是由于SMS与HWT的特征可以有效减小端元内部变化[10],并有效抵制光谱噪声的影响。在算法上,由于SMS算法中对所有的波段均等地对待,实际上不同波长的光谱对地物识别的贡献率是不相同的。如果在分割中对不同波段的贡献给予不同权重系数,等效于不均匀地拉大各波长的光谱差别,则在分割过程中权重系数大对应的光谱将会有更多的分割点。特别地,如果某些波段的权重设置为0,则表示分割过程中对这些波段不予考虑,等价于实施特征波段选择。因此,本文方法具有易于在分割过程中引入光谱先验信息的优点。由于本文采用各段光谱平均值近似表达对应光谱曲线,在分割数目较小时可能造成较大的光谱变形。如果在各分割段内采用直线形式的变化点模型[17],则可能会更好地刻画光谱曲线。此外,如何自动选取不同分割尺度下的光谱特征组合进行混合像元的分解也需要进一步研究。
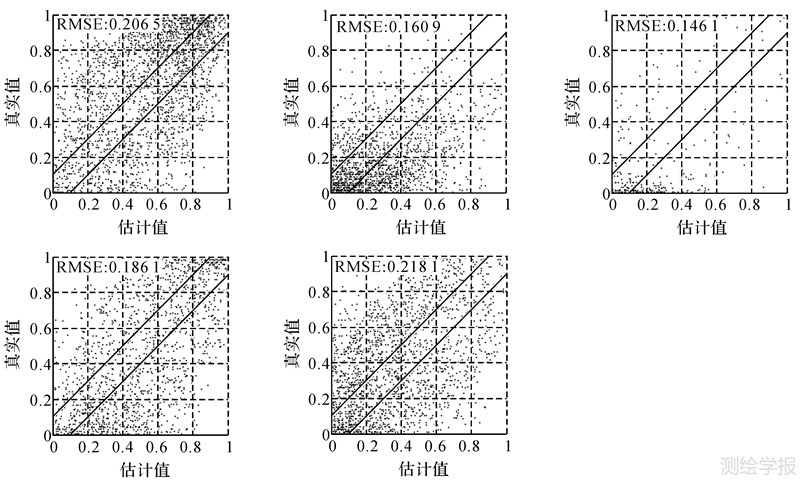
|
| 图 7 真实数据分解结果的BDF评价 Fig. 7 Accuracy assessment with BDF for real data |
针对混合像元线性分解的特点,提出一种基于光谱多尺度分割特征的混合像元分解方法。该方法具有自适应及多尺度分割等优点,能够较好地刻画光谱曲线特征,改善端元光谱矩阵结构。通过对模拟的与真实的数据试验分析,表明本文提出的方法能够显著地提高混合像元的分解精度。模拟数据的结果表明本文方法较原始光谱分解精度大约有41%的提高,相对与光谱维小波特征提取的方法,也有10%的提高。真实数据的结果表明本文相对原始光谱分解方法有2.7%的提高,相对与光谱维小波特征提取的方法,也有大约2%的提高。
| [1] | ZHAO Yingshi.The Principle and Method of Analysis of Remote Sensing Application[M].2nd ed.Beijing:Science Press,2003.(赵英时.遥感应用分析原理与方法[M].2版.北京:科学出版社,2003.) |
| [2] | WU Bo,ZHOU Xiaocheng,ZHAO Yindi.Study on the Relationships between End-member Variance and Decomposition Accuracy of Mixture Pixel[J].Chinese Remote Sensing Information,2007,28(3):3-8.(吴波,周小成,赵银娣.端元光谱变化与混合像元分解精度的关系研究[J].遥感信息,2007,28(3):3-8.) |
| [3] | PENN B S.Using Simulated Annealing to Obtain Optimal Linear Endmember Mixtures of Hyper Spectral Data[J].Computers&Geosciences,2002,28(7):809-817. |
| [4] | NASCIMENTO J M P,BIOUCAS D J M.Vertex Component Analysis:A Fast Algorithm to Unmix Hyperspectral Data[J].IEEE Transactions on Geoscience and Remote Sensing,2005,43(4):898-910. |
| [5] | JIA S,QUAN Y,Constrained Nonnegative Matrix Factorization for Hyperspectral Unmixing[J].IEEE Transactions on Geoscience and Remote Sensing,2009,41(7):161-173. |
| [6] | WANG J,CHANG C I.Applications of Independent Component Analysis in Endmember Extraction and Abundance Quantification for Hyperspectral Imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2006,44(9):2601-2616. |
| [7] | LIU W G,WU E Y.Comparison of Nonlinear Mixture Models:Sub-pixel Classification[J].Remote Sensing of Environment,2005,94(2):145-154. |
| [8] | WANG Xuhong,GUO Jianming,JIA Baijun,et al.Mixed Pixels Classification of Remote Sensing Images Based on Cellar Automata[J].Acta Geodaetica et Cartographica Sinica,2008,37(1):42-48.(王旭红,郭建明,贾百俊,等.元胞自动机的遥感影像混合像元分类[J].测绘学报,2008,37(1):42-48.) |
| [9] | CAI S,DU Q,Robert J M.Hyperspectral Imagery Visualization Using Double Layers[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(10):3028-3036. |
| [10] | ZHANG J,BENOIT R,ARTURO S A.Derivative Spectral Unmixing of Hyperspectral Data Applied to Mixtures of Lichen and Rock[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(9):1934-1940. |
| [11] | LI J,BRUCE LM.Wavelet-based Feature Extraction for Improved Endmember Abundance Estimation in Linear Unmixing of Hyperspectral Signals[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(3):644-649. |
| [12] | THEODORIDIS S,KOUTROUMBAS K.Pattern Recognition[M].4th ed.Beijing:China Machine Press,2009:375-387.(西奥多里德斯,考特罗姆巴斯.模式识别[M].4版.北京:机械工业出版社,2009:375-387.) |
| [13] | BELLMAN R.On the Approximation of Curves by Line Segments Using Dynamic Programming[J].Communications of the ACM,1961,4(6):284. |
| [14] | HEINZ D,CHANG C I.Fully Constrained Least Squares Linear Mixture Analysis for Material Quantification in Hyperspectral Imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2001,39(3):529-545. |
| [15] | FOODY G M.Thematic Map Comparison:Evaluating the Statistical Significance of Differences in Classification Accuracy[J].Photogrammetric Engineering and Remote Sensing.2004,70(5):627-633. |
| [16] | KLATT J W.Error Characterization of Spectral of Products Using a Factorial Designed Experiment[D].Rochester:Rochester Institute of Technology,2001. |
| [17] | AUE A,HORVATH L,HUAKOVÁ M,et al.Change-point Monitoring in Linear Models[J].Econometrics Journal.2006,9(3):373-403. |