2. 中南大学 地球科学与信息物理学院,湖南 长沙 410083
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China
1 引 言
地质体三维空间形态模拟是三维地学研究的一项基础性工作,它对地质形态构造研究、矿体品位储量估算、地下矿产勘查与采矿等都具有非常重要的意义,但由于受地质条件以及勘查技术的局限,地质勘查测量不可能获取到完整且规则的地质体数据。因此,根据勘探测量等方式所采集到的少量且分散的不完备数据建立接近真实的地质体三维空间可视化模型,是目前地学研究中的难点问题。
在地质体三维建模研究方面,早在20世纪90年代初,文献[1]就首先研究了规则三维格网(regular 3D grid)、非规则块(irregular block)、断面(sectional)和体(volume)数据结构,系统地建立了三维地质建模理论[1]。此后,许多学者对三维地质建模与可视化技术进行了大量的研究与实际应用工作,如:基于类三棱柱体的三维数据模型[2]、似三棱柱构模方法[3]、复杂地质体三维建模[4,5,6,7,8]、三维地质多体建模方法[9]等的研究以及各种地质体模型的建模与应用[10,11,12,13,14]。随着三维地质建模理论和技术的成熟,地质体三维建模与可视化技术得到了快速发展并已进入实用化阶段,市面上出现了大量的三维地质建模软件,如澳大利亚Maptek公司的Maptek Vulcan软件、英国Datamine公司的Datamine Studio软件、澳大利亚Surpac公司的Surpac Vision软件、法国Nancy大学开发的GOCAD地质建模软件、澳大利亚Micromine公司的Micromine软件;国内三地曼公司的3DMine软件、迪迈公司的Dimine软件,以及QuantyView和Titan 3DM等三维地质建模软件。采用上述三维地质建模技术(3DGM)与软件能够实现对各种地质体(如地层、构造、矿体等)的三维可视化模拟,但已有的三维地质建模软件一般是按照显式模拟的方法,即首先基于勘探工程数据绘制勘探线剖面,再在三维可视化环境下按剖面人机交互圈定地质界线并生成地质体三维模型,过程较为繁琐。随着三维可视化各种算法的发展与成熟,将不完备的样品数据通过空间插值来生成完备的样品数据,然后通过三维曲面构建等算法自动生成三维可视化模型的隐式模拟方法[15,16,17],在模型自动生成、快速适应新数据以及结果的精确性方面越来越显示出其优越性,目前已经成为许多领域解决技术问题的不可或缺的重要技术。
移动立方体算法(marching cubes,MC)是一种三维数据场等值面提取的经典算法[18,19,20]。近年来,移动立方体算法在医学影像数据的三维重建[21,22],有限元计算中的标量场分析,分子化学中的分子表面显示以及地学三维形态模拟[23,24]等方面得到广泛研究及应用,并取得了大量的研究成果。
本文基于不规则的钻孔样品数据,提出了一种基于移动立方体算法实现由网格离散点到地质体三维等值面的模拟方法:首先将离散的不规则数据进行网格化,然后利用移动立方体算法提取出由无数小三角面组成的地质体等值曲面,最后通过OpenGL提供的接口将这些小三角面片在屏幕上进行真三维显示,并设置相应的参数,构建了具有真实感的地质(矿)体三维空间形态可视化模型。
2 移动立方体算法原理[18,25,26,27,28]移动立方体算法被用于三维重建方面的相关研究,该算法是三维数据场等值面提取的经典算法,也是隐式模拟技术的代表,此算法在三维空间规则数据场的基础上,对数据场中的每个体元立方体(图1)逐个进行处理,依次找出每个体元中所包含的等值曲面。等值曲面是指三维空间中的一张曲面,在该曲面上的点的函数值等于一个给定的阈值c。{(x,y,z)|f(x,y,z)=c},其中c为设置的阈值大小。

|
| 图 1 体元立方体的定义 Fig. 1 The definition of cube |
每个体元中并非都存在等值面,当体元的8个顶点值都大于或都小于阈值c时,体元的内部不存在等值面。只有在既包含大于c的顶点也包含小于c的顶点的体元内部才存在等值面。
移动立方体算法过程如下:
(1) 每次读出两张切片,形成一层Layer;
(2) 两张切片上下相对应的4个点构成一个立方体;
(3) 依次从左至右,从前到后,顺序处理每一层中的立方体,抽取出各个立方体的等值面,并从下到上逐步处理(n-1)层。
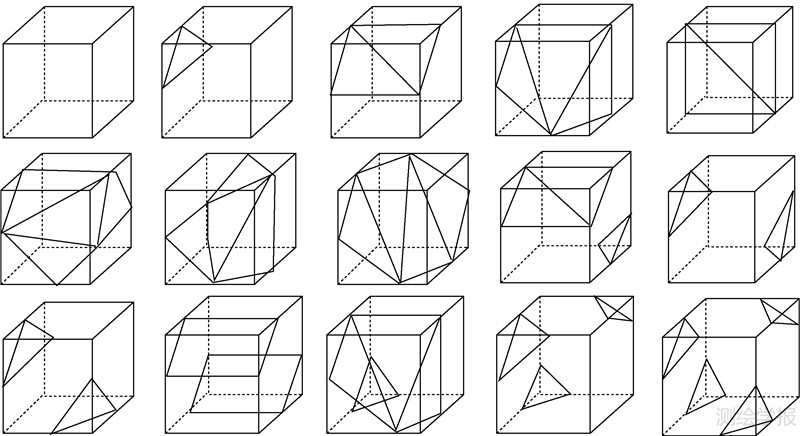
对于每个立方体来说,8个顶点的灰度值可以直接从输入数据中得到,并设定抽取的等值面的阈值。如果一个顶点的灰度值大于阈值,则将它标记为"1",小于阈值标记为"0"。等值面的分布总共可能有28=256种。由于立方体有旋转对称性而不影响等值面的拓扑关系,可以总结出15种基本的立方体(图2),它们可覆盖所有256种可能的拓扑关系。根据这15种基本立方体,可构造出一个表的长度为256的查找表,记录所有拓扑关系下的等值面连接方式,分别比较一个立方体的8个顶点值与阈值之间的大小关系,可得到一个0~255之间的索引值,通过查找表即可得到体元各个边上是否存在等值点。获取等值点的连接方式,将等值点连接起来形成逼近等值面的边界多边形,并进行三角化可得到最终的逼近等值面片。
传统的移动立方体算法将等值面与立方体边的交点连接生成等值面时,在立方体的一个面上如果值为"1"的顶点和值为"0"的顶点分别位于对角线的两端,就会有两种可能的连接方式,存在着二义性。同时,设定阈值后,该算法需检查每个立方体是否与等值面相交,许多时间花费在检查空立方体上,即与等值面没有相交的立方体,这将会大大降低重建的效率。
随着移动立方体算法的广泛应用,针对算法存在的二义性与计算量大的问题,出现了各种各样的改进算法,如消除二义性的双曲线判别方法、立体单元剖分法[29];提高算法效率的不同线性插值方法和基于区域分割的快速查找法等[30]。
考虑到本文采用的是研究区地质空间网格化的规则立体单元,且立体单元的矿化属性值通过估算确定,本文采用了剖分法[25]消除算法的二义性。如图 3所示,针对歧义面上等值线的两种不同连接方式direct型和reverse型,利用线性插值求出歧义面上4条边的中点以及中心点的坐标和函数值,将原来的正方形剖分为4个小的正方形。计算每个正方形各边上的等值点。当小正方形的4条边上只有两个等值点时,连接这两个等值点形成等值线;当仍有4个等值点时,继续剖分该小正方形,直到所有的小正方形都只有两个等值点时结束。将各个小正方形中的两个等值点用直线连接起来,自动生成立方体面上的等值线,从而消除了二义性问题。

|
| 图 3 消除等值面连接二义性的立体单元剖分 Fig. 3 The cube subdivision for eliminating the isosurface ambiguity |
由于三维地质空间中每个三维立方体信息网格实质上可看做是拓扑立方体网格,而每个三维立方体中心点坐标及属性数据保存在数据库中,采用这种剖分方式实现容易,本文试验中仅剖分一次就基本上消除了二义性。
同时在程序中通过单元属性值与所设阈值的比较,首先判别出非空的立方体,即与等值面相交的立方体,并设置一个队列进行保存,使得与等值面相交的非空立方体能被快速有效地检查到,大大减少了检查空立方体的时间。实际上,对于地质曲面模拟,先基于阈值,逐个判断立方体是否为空,记录非空立方体的同时在表中保存其相邻的立方体,如果某个立方体被确认为非空,那么与它相邻的立方体中的三角形面片会沿着一定方向扩展,而与它相邻的立方体在表中将会被快速地找到,从而可以提高地质曲面三维重建的效率。
3 地质体三维空间形态隐式模拟方法 3.1 基于移动立方体算法的三维地质体模拟流程本研究中,基于少量离散且不规则地质体数据的三维空间形态模拟是结合移动立方体算法和OpenGL三维可视化技术来实现的。首先需要对离散的地质体数据进行内插计算和处理,将分散的不规则分布的钻孔数据转换成规则分布的网格数据,构建三维空间规则数据场。详细的模拟技术流程如图4所示。

|
| 图 4 三维空间形态隐式模拟技术流程 Fig. 4 The process of three-dimensional spatial shape simulation |
从研究区地质资料数据库中提取与地质体有关的原始数据,这些实测资料和数据包括地质剖面图、勘探工程数据和各种样品化验表格数据等。数据预处理是指通过对这些资料和表格进行分析和处理,获取研究区域地质体已知的空间数据和属性数据,为利用空间插值方法实现数据网格化,推断并预测研究区未知区域地质体信息的分布趋势作准备。然后依据移动立方体算法,从三维规则数据场中提取出由无数小三角面组成的等值面。最后结合OpenGL可视化技术为虚拟场景中的地质体构建三维几何模型。
3.2 三维空间规则数据场构建方法由于实际应用中获取到的钻孔数据基本都是采样稀疏的不规则数据,需通过插值算法估计出一系列点缺失的观测数据,以提高钻孔数据的密度。数据网格化是对连续量或连续体按一定精度进行抽样的过程,一般采用三维栅格的方法对地质空间进行分割抽样,分割后得到的各个栅格称为立体单元。地质空间分割的精度决定立体网格单元的大小,与矿床勘探程度等因素相关。地质空间经过抽样分割网格化后,对地质体属性按网格单元进行数据量化取值与编码,从而构建地质体三维空间规则数据场。
基于离散且不规则的地质体属性数据的网格化过程需要利用空间插值方法来实现。由于地质数据有其特殊的特点,在进行空间数据插值时,不能简单地套用现成的自动插值方法,必须考虑许多制约因素及相关的地质学原理,目前以几何方法和空间统计方法在地学领域最为常用。如克里金(Kriging)法、径向基人工神经网络(radial basis function,RBF)法等作为插值方法在地学建模和矿产资源储量估算中都有广泛的应用。对于连续的三维矿化空间,能够基于离散的数据直接选用合适的方法实现网格数据的插值;对于带断层的地层等不连续地质体空间的插值则可以先通过断层线确定包络范围,进行局部插值。
本文使用的数据主要来自于钻孔勘探数据,首先通过钻孔测斜计算,计算出钻孔拐点的坐标,再采用线性插值的方法计算出落在任意两个拐点间的钻孔采样点空间坐标,最后按照划分的网格立体单元中心坐标,判断有采样点落入的网格单元作为已知单元,取落入的采样点品位数据平均值作为其品位值。在多个不同钻孔采样数据点覆盖的深度范围,考虑方法和模型的适应性,采用克里金插值方法完全可以实现未知网格单元(无采样点落入)的品位推估,建立三维矿化空间规则数据场。但由于本文中的网格化实例数据来自于矿山深边部隐伏矿体预测项目(见本文实例),需要对没有钻孔控制和采样点数据的深部(-1000m以上)、边部立体单元矿化值进行推估,而克里金法并不适应。因此考虑到成矿地质条件的复杂性,实例三维数据场中未知网格单元含矿性的推估经过了从成矿信息定量提取到控矿因素与矿化分布的定量分析,以及隐伏矿体立体定量预测建模的过程[14]。最后将三维空间网格单元的位置与矿化信息保存在数据库中。
3.3 基于OpenGL的三维地质体可视化OpenGL是一种开放的图形程序接口,适合于各种计算机操作系统下的三维图形应用程序编程,是一个功能强大,方便调用的底层3D图形库。三维地质体可视化研究可基于OpenGL图形接口将大量数据以图形或图像的方式表达出来,使抽象的数据内容变得形象、直观。OpenGL提供了大量图形变换函数,能够在虚拟场景中构建三维地质体几何模型,然后根据观察点的位置及观察方式进行变换和投影,最后实时绘制场景,方便地将地质体三维空间形态模型展示出来。对三维地质体的曲面进行光照、着色以及融合处理等细化加工,使矿体呈现一种透明或半透明的状态,还可通过增加缩放、旋转等图像增强效果功能,使地质体更加逼真地呈现出来。由于在地质(矿)体渲染过程中产生大量的三角片,且在交互式观察地质体过程中需实时渲染场景,因此对计算机性能要求较高。要想提高模型的精度并且作到快速实时渲染,就要求有大容量的内存和高效的CPU,对大量网格数据的三维规则数据场显示和地质曲面重建还需要研究相应算法的改进。
4 实 例 4.1 实例数据以安徽铜陵凤凰山矿田铜矿床地质空间中的铜矿体为研究对象,以钻孔勘探数据为原始数据,建立Access数据库,采用移动立方体算法与OpenGL可视化技术编程实现铜矿体的三维空间形态模拟。本文的研究区范围来自于凤凰山矿田深边部隐伏矿体预测的研究项目,考虑到矿田已有的地质工作程度、研究工作的目标及范围,项目定义了一个巨大的立方体空间作为地质空间的包集。试验中为了与显示模拟的矿体三维可视化模型进行比较,选取了钻孔深度范围-475~275 m的地质空间作为研究区数据网格化区域,对研究区按50 m×50 m×50 m划分地质空间,总共分成159 030个立方体单元。
钻孔数据包括开孔数据表(collar),测斜数据表(survey),采样品位数据表(sample),这些数据表结构如表1至表3所示[27]。
| 列名 | 含义 | 数据类型 | 固有字段 |
| BHID | 工程名 | 文本 | 是 |
| XCOLLAR | 开孔X坐标 | 数字 | 是 |
| YCOLLAR | 开孔Y坐标 | 数字 | 是 |
| ZCOLLAR | 开孔Z坐标 | 数字 | 是 |
| SECTION | 勘探线 | 文本 | 否 |
| 列名 | 含义 | 数据类型 | 固有字段 |
| BHID | 工程名 | 文本 | 是 |
| AT | 孔深 | 数字 | 是 |
| NUM | 测斜点编号 | 数字 | 是 |
| DIP | 测斜倾角 | 数字 | 是 |
| BRG | 测斜方位角 | 数字 | 是 |
| 列名 | 含义 | 数据类型 | 固有字段 |
| BHID | 工程名 | 文本 | 是 |
| FROM | 样品起始深度 | 数字 | 是 |
| TO | 样品终止深度 | 数字 | 是 |
| SECTION | 勘探线 | 文本 | 否 |
| Cu | 铜含量 | 数字 | 否 |
| OreID | 矿体编号 | 文本 | 否 |
凤凰山矿田铜矿床原始钻孔取样数据是由提取的钻孔岩芯取样化验结果组成,为了定量评价矿体的分布和产状,必须通过实现这些化验结果的空间化得到各取样点的坐标。根据铜陵凤凰山钻孔测斜计算,计算出每个测斜点所控制的边界点(拐点)的坐标与孔深,按表3中样品起始深度与终止深度,求取中点井深作为采样点井深,判断其落在哪两个拐点之间,通过线性插值求出采样点坐标,最后得出钻孔采样点位表,表结构如表4所示。按采样点坐标找出落在相应网格立方体单元中的采样点,对落在每个单元的所有采样点的铜品位取平均值,共获得6317个含矿立方体已知单元数据[27]。
| 字段名 | 字段类型 | 长度 | 描述 |
| 采样编号 | char | 6 | 采样点编号 |
| 孔号 | char | 6 | 钻孔编号 |
| 采样点井深 | float | 小数位2 | 样长中点井深 |
| 采样点X | float | 小数位3 | 采样点X坐标 |
| 采样点Y | float | 小数位3 | 采样点Y坐标 |
| 采样点Z | float | 小数位3 | 采样点Z坐标 |
| Cu/(%) | single | 小数位3 | 化学元素分析 |
| Zn/(%) | single | 小数位3 | 化学元素分析 |
| | | | |
| 备注 | char | 30 | 有关说明 |
未知单元含矿值的推估根据项目中矿化分布的预测模型[14]获得。图5为项目中开发的网格立体单元水平分层三维可视化查询界面,从数据库中读取每一层的三维立体信息网格数据,包括其中心点坐标和属性信息,通过坐标中隐含的三维立体信息网格拓扑关系,连接数据库时将三维网格依次编号,将带有编号ID的网格信息推入链表,再根据链表信息,对三维地质空间进行栅格绘制。每隔50 m水平可进行分层查询网格立体单元的铜品位值,红色代表已知单元矿化信息区域,绿色代表未知单元但单元铜品位预测值已达工业品位的预测含矿区域,蓝色则代表未知单元但铜品位预测值小于工业品位的预测不含矿区域。

|
| 图 5 网格化立体单元矿化值可视化水平分层查询 Fig. 5 Raster model showing the three-dimensional visualization mineral results for any cube in a layer |
基于研究区网格立体单元数据,结合移动立方体算法和OpenGL可视化技术采用C++编程实现了三维铜矿体的模拟。设置等值面阈值的铜含量为0.3%(铜的工业品位值),在程序中首先对非空立方体单元进行了判断,三维铜矿体等值面生成所耗费的时间大约为7.560 s,经过三角化后生成的三角片数量为350 300个(机器配置:AMD Athlon (tm) II X2 B24 Processor 2.99 GHz,2.00 GB内存,320 GB硬盘)。图6为凤凰山铜矿体的三维可视化效果。

|
| 图 6 铜矿体隐式模拟结果图 Fig. 6 The implicit simulation result of isosurface extraction for Cu |
从图6隐式模拟的结果看,基本反映矿体的三维空间分布规律,参考手工勾绘的勘探剖面图资料,3个主要的曲面群对应矿山3个主要矿体的位置,与在Datamine软件中人工交互式圈定的矿体显式模拟结果(如图7所示)相比,形状和大小相近。但从细节上看有些差异,隐式模拟的矿体边界相对光滑,同时模拟结果中有一些零星的小曲面。这主要是因为通过推估模型获得的某些空间网格矿化值存在偏差,同时,基于移动立方体算法在自动构建邻近数据点的等值面时总是以圆滑曲面生成。但相对显式模拟,隐式模拟省却了繁琐的人工圈定过程。

|
| 图 7 显式模拟栅格化结果 Fig. 7 The result of explicit simulation |
在地质体数据不足的情况下,利用空间插值方法对数据进行网格化,推断并预测未知区域及研究较少区域的地质体信息的分布趋势,结合移动立方体算法与OpenGL可视化技术编程,能有效对不规则勘查数据自动实现地质要素数据场的三维形态模拟。这种方法在矿业开发前期能够快速得到地下要素信息的三维可视化表达,帮助地质工作者形象直观地分析地质特征并处理大量的野外测量和样品分析数据,有效地指导矿业开发。但针对不同的地质条件和地质体数据,如何选择合适的空间插值方法与模型,还有待进一步研究和验证,另外,基于改进的移动立方体算法对不同地质体模拟的适应性以及断层等线性不连续层位面片的构造也将在后续工作中作进一步研究。
| [1] | SIMON W. Holding 3D Geoscientific Modeling Computer Technique for Geological Characterization [M]. Hongkong:South Sea Int Press,1994. |
| [2] | WU Lixin, ZHANG Ruixin, QI Yixin, et al. 3D GeoScience Modelling and Virtual Mine System [J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(1): 28-33. (吴立新, 张瑞新, 戚宜欣, 等. 三维地学模拟与虚拟矿山系统[J]. 测绘学报, 2002, 31(1): 28-33.) |
| [3] | CHENG Penggen, GONG Jianya, SHI Wenzhong, et al. Geological Object Modeling Based on Quasi Tri-prism Volume and Its Application [J]. Geomatics and Information Science of Wuhan University, 2004, 29(7): 602-607. (程朋根, 龚健雅, 史文中, 等. 基于似三棱柱体的地质体三维建模与应用研究[J]. 武汉大学学报:信息科学版, 2004, 29(7): 602-607.) |
| [4] | SUN Min, XUE Yong, MA Ainai, et al. Reconstruction of 3D Complex Geological Bodies Based on Tetrahedron Mesh [J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(4): 361-365.(孙敏, 薛勇, 马蔼乃, 等. 基于四面体格网的三维复杂地质体重构[J]. 测绘学报, 2002, 31(4): 361-365.) |
| [5] | ARENS C, STOTER J, VAN OOSTEROM P. Modelling 3D Spatial Objects in a Geo-DBMS Using a 3D Primitive[J]. Computers and Geosciences, 2005, 31(2): 165-177. |
| [6] | PAN Mao, FANG Yu, QU Honggang. Discussion on Several Foundational Issues in Three-Dimensional Geological Modeling[J]. Geography and Geo-Information Science, 2007, 23(3): 1-5.(潘懋,方裕,屈红刚. 三维地质建模若干基本问题探讨[J].地理与地理信息科学,2007, 23(3): 1-5.) |
| [7] | WANG Runhuai, LI Yongshu. Introduction and Determination of Borderline Virtual Boreholes in 3D Modeling of Complicated Geological Bodies [J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 465-475. (王润怀, 李永树. 边界虚拟钻孔在复杂地质体三维建模中的引入与确定[J]. 测绘学报, 2007, 36(4): 465-475.) |
| [8] | ZANCHI A, FRANCESCA S, STEFANO Z, et al. 3D Reconstruction of Complex Geological Bodies: Examples from the Alps. [J]. Computers and Geosciences, 2009, 35(1): 49-69. |
| [9] | MING Jing, PAN Mao, QU Honggang, et al. GSIS: A 3D Geological Multi-body Modeling System from Netty Cross-sections with Topology [J]. Computers and Geosciences, 2010, 36 (6): 756-767. |
| [10] | GUILLEN A., CALCAGNO P, COURRIOUX G, et al. Geological Modeling from Field Data and Geological Knowledge, Part II. Modelling Validation Using Gravity and Magnetic Data Inversion[J]. Physics of the Earth and Planetary Interiors, 2008,171:158-169. |
| [11] | KAUFMANN O, MARTIN T. 3D Geological Modelling from Boreholes, Cross-sections and Geological Maps, Application over Former Natural Gas Storages in Coal Mines[J]. Computers and Geosciences, 2008, 34(3): 278-290. |
| [12] | ZOU Yanhong, ZHOU Sheng, CHEN Jin, et al. Geological Bodies' Modality Analysis Based on 3D Visualization Environment[J]. Geomatics World, 2008,6(5):33-38.(邹艳红, 周胜, 陈进,等. 基于三维可视化环境的地质体空间形态分析[J]. 地理信息世界,2008, 6(5):33-38.) |
| [13] | LI Yin,XIAO Keyan,CHEN Jianping. Ore Body Simulation and Resource Assessment Based on Three-dimensional Cube Model[J]. Geological Bulletin of China,2010,29(10):1547-1553.(李莹,肖克炎,陈建平. 基于立方体模型的三维矿体模拟与资源评估[J].地质通报,2010, 29(10): 1547-1553.) |
| [14] | MAO Xiancheng, ZOU Yanhong, CHEN Jin, et al. Three-dimensional Visual Prediction of Concealed Ore Bodies in the Deep and Marginal Parts of Crisis Mines: A Case Study of the Fenghuangshan Ore Field in Tongling, Anhui[J]. Geological Bulletin of China,2010, 29(2-3): 401-413. (毛先成,邹艳红,陈进,等. 危机矿山深部、边部隐伏矿体的三维可视化预测-以安徽铜陵凤凰山矿田为例[J]. 地质通报,2010, 29(2-3): 401-413.) |
| [15] | TURK G,O’BRIEN J F. Shape Transformation Using Variational Implicit Functions[C]//Computers and Graphics Proceedings, Annual Conference Series (SIG GRAPH 1999). New York : ACM Press,1999: 336-342. |
| [16] | MORSE B S, YOO T S, RHEINGANS P, et al. Interpolating Implicit Surfaces from Scattered Surface Data Using Compactly Supported Radial Basis Functions[C]//Proceedings of Shape Modeling Conference.Genova: IEEE, 2001:89-98. |
| [17] | COWAN E J, BEATSON R K, ROSSH J, et al. Practical Implicit Geological Modeling[C]//Proceedings of 5th International Mining Geology Conference.Carlton South: The Australasian Institute of Mining and Metallurgy, 2003: 89-99. |
| [18] | LORENSON W, CLINE H. Marching Cubes: A High Resolution 3D Surface Construction Algorithm[J].Computer Graphics, 1987, 21 (4): 163-169. |
| [19] | SHEKHAR R, FAYYAD E, YAGEL R, et al. Octree-based Decimation of Marching Cubes Surfaces[C]//Proceedings of Visualization'96. San Francisco: IEEE, 1996: 335-342. |
| [20] | SCHAEFER S, WARREN J. Dual Marching Cubes: Primal Contouring of Dual Grids [J]. Computer Graphics Forum, 2005, 24(2): 195-201. |
| [21] | LIU Shaoli, YANG Xiangdong, CHEN Ken. Segmentation MC Algorithm-based Method for Ultrasound Image 3D Reconstruction[J]. Journal of Tsinghua University: Science and Technology, 2010, 50(8): 1214-1218.(刘少丽, 杨向东, 陈恳. 基于分割MC算法的超声影像三维重建方法[J]. 清华大学学报:自然科学版, 2010, 50(8): 1214-1218.) |
| [22] | LIU Haihua, WAN Shuang, LU Xuesong. The Multi-Storey Medical Image Reconstruction Based on Marching Cubes Algorithm [J]. Journal of South-Central University for Nationalities: Natural Sciences Edition, 2009, 28(3): 79-84. (刘海华,万双, 陆雪松. 基于Marching Cubes算法的多层医学图像重建实现[J]. 中南民族大学学报:自然科学版, 2009, 28(3): 79-84.) |
| [23] | LI Suyun, TANG Jie, WU Gangshan. Algorithm of Geology Mesh Surface Reconstruction Based on Constraints[J]. Computer Engineering, 2009, 35(1): 253-254.(李素云,唐杰,武港山.基于约束的地质网格曲面重建算法[J]. 计算机工程, 2009, 35(1): 253-254.) |
| [24] | YANG Hongyi, LIU Liangming, ZHAO Yilai. 3D Geological Modelling Based on Kriging and Marching Cube Algorithm[J]. Journal of Image and Graphics, 2008, 13(3): 531-535.(杨鸿翼,刘亮明,赵义来.基于Kriging和Marching Cube算法的地学三维形态模拟[J].中国图象图形学报,2008,13(3): 531-535.) |
| [25] | ZHOU Yan.Study on Three-dimensional Visualization of Medical CT Images[D].Chongqing: Chongqing University,2005.(周宴.CT 图像的三维可视化技术研究[D].重庆:重庆大学,2005.) |
| [26] | LI Jing,HU Zhanli.3D Reconstruction of Medical Images Based on Marching Cubes and Ray Casting[J]. Life Science Instruments, 2007(12):40-43.(李金,胡战利.基于Marching Cubes与Ray Casting的医学图像三维重建[J]. 生命科学仪器, 2007(12):40-43.) |
| [27] | HE Jianchun.Research on Technologies of Three Dimensional Spatial Morphology Implicit Simulation for Geological Body[D].Changsha: Central South University,2011.( 何建春.地质体三维空间形态隐式模拟的若干技术研究[D].长沙:中南大学,2011.) |
| [28] | ZOU Yanhong.Research on Geologieal,Surveying Data Integration and Three Dimensional Cubic Quantitative Visualization Prognosis in Mine[D].Changsha: Central South University,2005.( 邹艳红.矿山地测数据集成与三维立体定量可视化预测研究[D]. 长沙:中南大学,2005.) |
| [29] | YU Shicai, TANG Zhanhong. Study on the MC Three-dimensional Reconstruction Algorithm and Eliminate It’s Ambiguity[J]. Micro Computer Information, 2009, 25(8-3): 222-224.( 於时才, 唐占红. MC三维重建算法的二义性消除研究[J]. 微计算机信息,2009,25(8-3):222-224.) |
| [30] | QIAN Feng, MA Xiuli, YANG Shengqi, et al. Research and Improvement of Marching Cubes Algorithm[J].Computer Engineering and Applications,2010,46(34):177-180.(钱峰,马秀丽,杨胜齐,等.移动立方体算法的研究和改进[J]. 计算机工程与应用, 2010,46(34): 177-180.) |