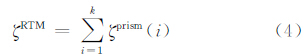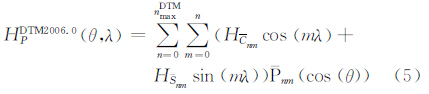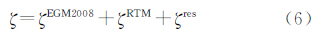2. 铁道第三勘察设计院集团有限公司 测绘分院,天津 300251
2. Department of Surveying and Mapping, The Third Surveying and Design Institute Group Corporation, Tianjin 300251, China
1 引 言
随着卫星重力计划的逐步实施和完善,利用卫星重力资料并结合地面重力数据获得的全球重力场模型的精度和分辨率在逐步提高,特别是EGM2008模型的公布[1],使得利用重力场模型进行GPS高程转换的精度和可靠性获得了大幅度提升。EGM2008模型的阶次完全至2159(另外球谐系数的阶扩展至2190,次为2159),相当于模型的空间分辨率为5′(约9 km)。EGM2008模型采用了GRACE卫星跟踪数据(ITG-GRACE03S位系数信息以及相应的协方差信息)、卫星测高数据和地面重力数据等,该模型无论在精度还是在分辨率方面均取得了巨大进步[2, 3]。文献[4]利用我国大陆GPS/水准实测高程异常对EGM2008地球重力场模型进行了外部精度测试,结果表明:EGM2008模型高程异常精度在我国大陆的整体精度为20 cm,且与全球精度相当。
地球重力场模型展开到一定的阶次,对应于一定的空间分辨率,EGM2008模型的阶数高达2190,也只有约9 km的空间分辨率,很难表示更高频段的高程异常。为了提高GPS高程转换的精度,须借助于高分辨率的地形模型。文献[5]推导出一套适合厘米级似大地水准面精化的Molodensky解实用简便的算法公式,并结合实例测试验证了厘米级地形影响的技术特征,文献[6, 7, 8]对RTM技术用于补偿EGM2008信号截断误差进行了研究,获得了良好的效果。笔者基于剩余地形模型理论[9, 10, 11],利用SRTM以及DTM2006.0全球地形模型构建RTM数据,并计算剩余地形模型高程异常。任意GPS点的总高程异常可表示为地球重力场模型高程异常、剩余地形模型高程异常以及残余高程异常3部分总和的形式,通过计算可获得所有GPS点总高程异常中的前两项,然后选择少量GPS/水准点的实测高程异常,扣除EGM2008模型以及SRTM与DTM2006.0模型求得的剩余模型高程异常,对残余高程异常进行拟合,从而提高GPS高程转换的精度。利用2个不同测区的高精度GPS/水准数据进行实例分析,结果表明,该方法能显著提高GPS高程转换精度。
2 原理与方法 2.1 重力场模型高程异常计算根据Bruns公式,地球表面上任意点P的模型高程异常可由下式获得[4]
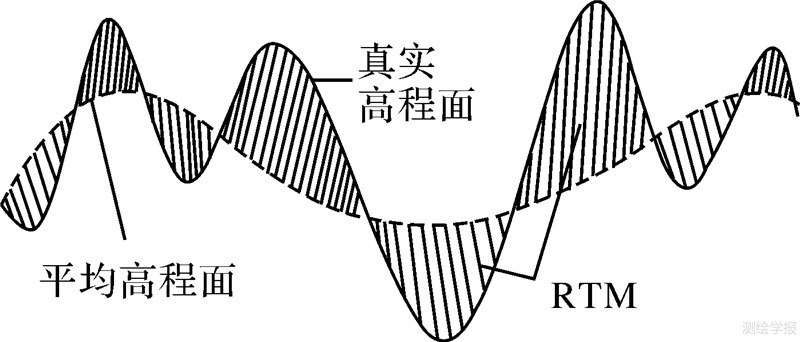
式中,Pnm(sin φ)为完全规格化Legndre函数;GM为地心引力常数;N为地球重力场模型展开的最高阶数,对于高阶Legndre函数计算要特别注意计算的稳定性[12];其他参数含义参见文献[4]。 2.2 剩余地形模型(RTM)高程异常计算RTM数据表示真实地形表面和参考地形表面的差值,见图 1。一般情况下,真实地形表面用分辨率较高的DTM数据表示,而参考地形表面用分辨率较低的DTM数据表示,该数据是对表示真实地形表面的DTM经过一定平滑处理后获得的。在地形起伏较大测区,仅仅依靠一定阶次的地球重力场模型以及少量的GPS/水准数据很难对短波长的重力场信号进行模型化,而这种方法又是非常经济实用的GPS高程转换方法,理论上RTM技术有能力表示由局部地形变化引起的重力场短波长部分。
|
| 图 1 剩余地形模型(RTM) Fig. 1 Residual terrain model |
RTM高程异常计算的方法很多,本文探讨利用棱柱积分法将RTM数据转换到剩余高程异常,每个棱柱(格网)对应的引力位为[13, 14]
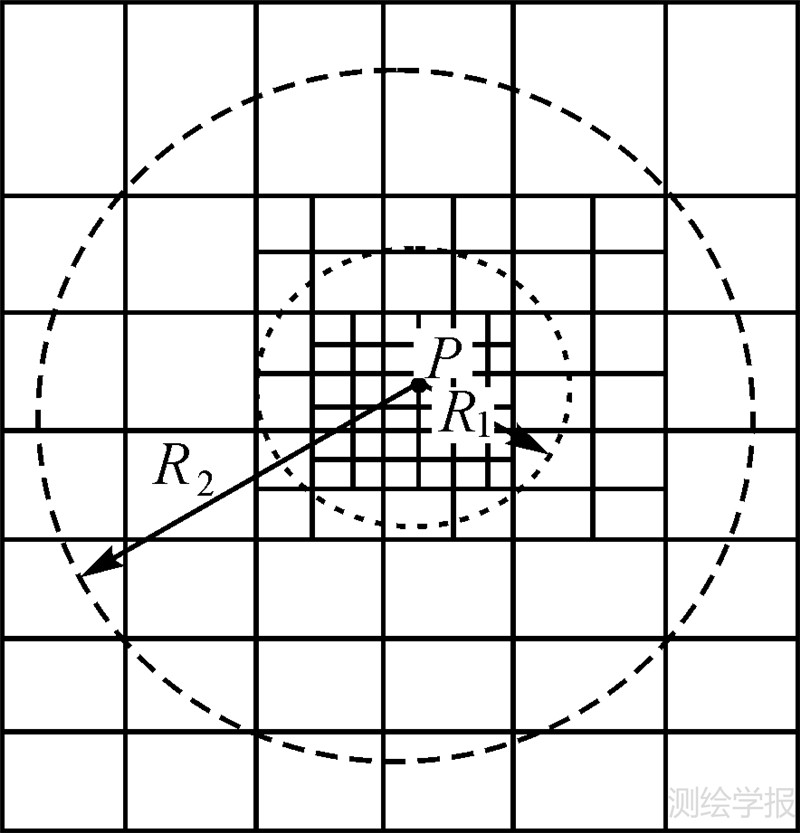
式中,G为引力常数;r为坐标原点到点(x,y,z)的距离;x1、x2、y1、y2、z1、z2为棱柱体的边界角点坐标,z2-z1表示剩余高程;ρ0为标准的地形质量密度,取ρ0=2670 kg/m3;式(2)是平面近似,计算中需考虑地球曲率的影响[11];其他变量的含义及具体计算过程请参考相关文献[11, 13, 14],将棱柱引力位转换为对应的高程异常,公式为 式中,γQ表示正常重力。GPS点P所对应的RTM高程异常可由计算区域内所有单个棱柱对应的高程异常总合表示,公式为为了提高棱柱积分的计算速度,在实际应用中,离计算点稍远的区域采用分辨率稍低DTM格网数据,离计算点较近的区域采用分辨率较高的DTM格网数据,这种实用的剩余地形计算的过程称为粗糙/详细DTM格网系统。在计算过程中,一般会给两个积分计算半径R1和R2,当积分半径小于R1时用详细格网数据,当积分半径在R1和R2时用粗糙格网数据。另外在计算点P周围3×3格网的地形数据用双三次样条函数进行加密处理,以获得更光滑的地形数据,这种加密也可避免计算点P处于格网边界时对计算结果产生影响[11],粗糙/详细DTM格网数据使用情况见图 2。
|
| 图 2 粗糙/详细 DTM格网使用情况图 Fig. 2 Use of coarse and detailed DTM grid |
利用RTM方法计算高程异常的关键是构建RTM数据。目前可用于RTM数据构建的全球DTM数据有3″的SRTM、1″的ASTER GDEM以及局部高精度的DTM数据等。在我国要获得局部高精度的DTM数据难度较大,而SRTM和GDEM数据是公开的,SRTM(V4.1)的高程精度要优于GDEM。本文RTM的构建方法为:①采用免费的3″ SRTM(V4.1)数据来表示地形表面,详细及粗糙DTM数据均由该数据获得;②一般情况下,参考面DTM可通过对3″ SRTM(V4.1)数据进行平滑、降低分辨率而获得,本文为了与EGM2008模型更匹配,参考面DTM数据采用EGM2008研发课题组完成的DTM2006.0模型;③利用①和②数据构建RTM数据,即zRTM=z2-z1=HSRTM-HDTM2006.0。
DTM2006.0模型是为满足新一代超高阶地球重力场模型(如:EGM2008)研发所涉及的与地形有关的重力量计算而完成的全球高分辨率DTM模型。该模型阶次为2190,容纳了大约240万对正规化的高程系数,地面上任意一点P的模型高程可用式(5)求得[15]
式中,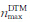 表示高程模型的最大阶数;HCnm和HSnm表示正规化的高程系数;(θ,λ)表示点P的坐标。DTM2006.0模型相当于高通滤波器,用于移去SRTM地形模型中的长波部分,由SRTM/DTM2006.0构建的RTM数据可表示比超高阶重力场模型EGM2008空间分辨率高的重力场高频信息。
2.4 综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的高程异常拟合
表示高程模型的最大阶数;HCnm和HSnm表示正规化的高程系数;(θ,λ)表示点P的坐标。DTM2006.0模型相当于高通滤波器,用于移去SRTM地形模型中的长波部分,由SRTM/DTM2006.0构建的RTM数据可表示比超高阶重力场模型EGM2008空间分辨率高的重力场高频信息。
2.4 综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的高程异常拟合
基于EGM2008模型,利用式(1)可获得任意GPS点的重力场模型高程异常ζEGM2008,由式(4)可获得剩余地形模型高程异常ζRTM,则任意点P总的高程异常为
式中,ζres表示残余高程异常。为提高GPS高程转换精度,在实际数据处理过程中,一般可采用如下方法:①基于EGM2008模型计算所有GPS点重力场模型高程异常ζEGM2008;②根据RTM数据计算所有GPS点的RTM高程异常ζRTM;③采用优化选择法选择少量GPS/水准点,计算这些点的实测高程异常,然后扣除模型高程异常ζEGM2008以及RTM高程异常ζRTM,获得残余高程异常ζres,利用一定的拟合方法建立残余高程异常拟合模型,从而推求待求GPS点残余高程异常,通过式(6)即可获得待求点的总高程异常。其中ζRTM和ζres可表示为EGM2008模型的截断误差。选择少量GPS/水准点的目的有两个:①建立残余高程异常拟合模型;②实现高程基准转换,即将EGM2008模型所对应的高程基准转换到水准点对应的高程基准。对于面状测区,待求点的残余高程异常可通过平面或曲面等拟合函数获得。而对于公路、铁路等线路测区,由于GPS点一般沿线路延伸方向呈近似直伸形式分布,若采用平面或曲面拟合函数,则需要在线路两侧联测足够多的GPS/水准点,否则容易造成观测方程病态。一般可选择某一GPS点作为坐标原点,以线路延伸方向作为坐标轴的横轴,过坐标原点且与横轴垂直的方向为纵轴建立线路独立坐标系,然后忽略垂直线路方向的高程异常变化,并利用直线、二次曲线或三次曲线拟合函数。在实际计算中选择不同的GPS/水准点,可能会得到不同精度的高程转换结果,因此有必要对GPS/水准点进行优化选择,可采用逐步剔除法[16]。
3 计算与结果分析为对本文提出的方法进行精度分析,现选择华南地区两个地形起伏相对较大测区GPS/水准数据作为测试数据:算例A(带状GPS/水准数据)和算例B(面状GPS/水准数据)。
3.1 计算数据准备为满足实际计算需要,本文共收集或计算了如下几组数据。
(1) 3″的SRTM数据:算例A(25°N-30°N,107°E-115°E)和算例B(23°N-27°N,111°E-116°E)3″的SRTM数据,该数据直接从SRTM官方网站获得,用于表示测区详细地形。
(2) 15″的SRTM数据:15″ SRTM数据是通过对3″ SRTM数据进行平滑处理获得,用于表示测区的粗糙地形。
(3) 参考面DTM数据:根据DTM2006.0模型利用式(5)计算了这两个测区相应范围的分辨率为30″的参考面DTM数据,模型阶次取2160。
(4) 高精度的GPS/水准点:算例A共收集到高精度GPS/水准点109个,算例B共收集到高精度GPS/水准点41个,两个算例的GPS点坐标基准均为CGCS2000大地坐标系,GPS点大地高精度均优于2 cm,水准测量等级不低于三等。
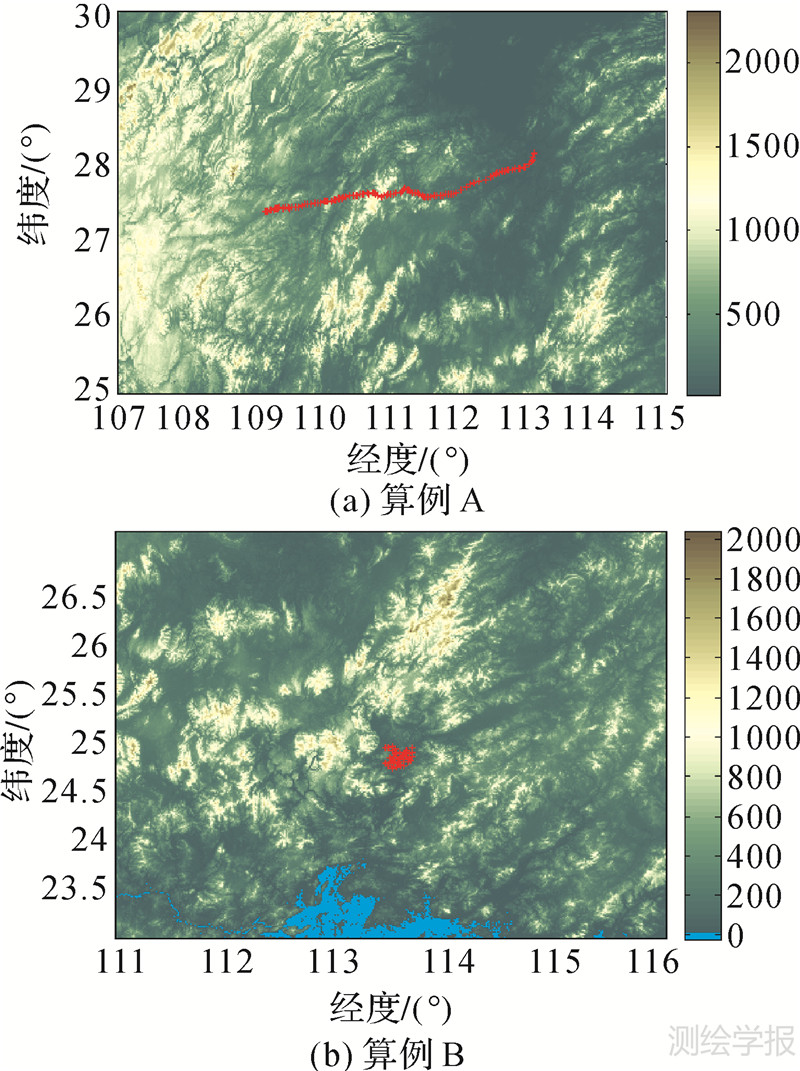
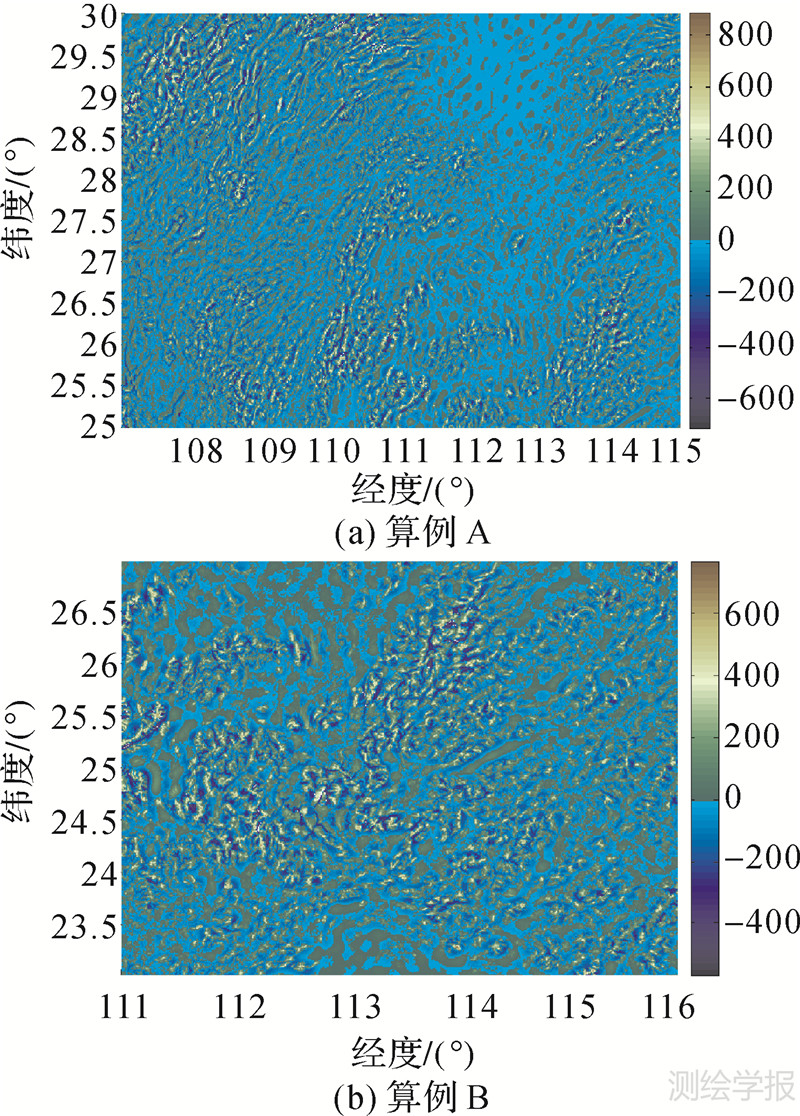
两个测区地形情况(15″的SRTM数据)和GPS/水准点概略点位见图 3,其中十字丝表示GPS/水准点。测区RTM高程数据见图 4(SRTM高程与DTM2006.0高程之差,分辨率为30″)。
|
| 图 3 测区地形(SRTM)及GPS/水准点 Fig. 3 SRTM terrain and GPS/leveling points |
|
| 图 4 测区RTM高程数据(SRTM-DTM2006.0) Fig. 4 RTM elevations(SRTM-DTM2006.0) |
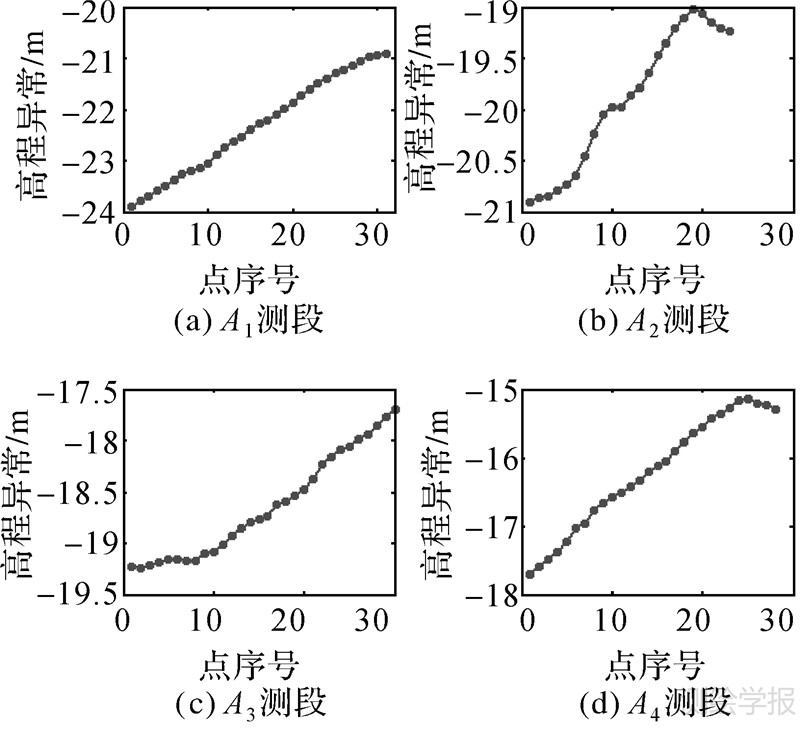
算例A为某一铁路客运专线GPS/水准数据,线路跨度近500 km,共有GPS/水准点109个,整个线路西部地势较东部高,东部GPS/水准点间距略比西部大,整个线路平均点间距约4.5 km。为对残余高程异常进行有效拟合,提高GPS高程转换精度,本文将整个线路GPS/水准数据分为4段:A1、A2、A3和A4,分段的基本过程和原则为:①鉴于EGM2008地球重力场模型具有很高的精度,本文首先利用2160阶次的EGM2008地球重力场模型计算所有GPS/水准点的模型高程异常;②沿线路走向绘制线路模型高程异常变化图;③在保证每段高程异常变化趋势基本一致或变化不大前提下,尽量延长线路长度,且每个测段宜近似直线走向。A1、A2、A3和A4测段模型高程异常变化图见图 5,每个图横轴表示该测段点序号,整个测区高程异常变化约9 m。
|
| 图 5 算例A测区高程异常变化图 Fig. 5 The height anomaly variability for case A |
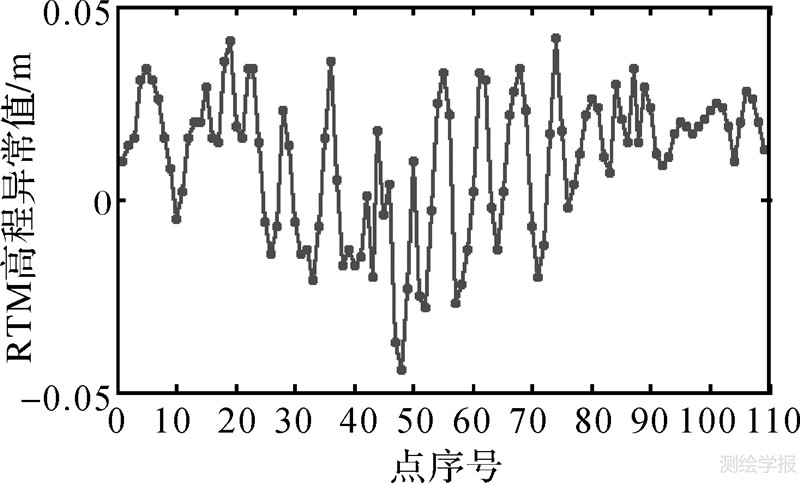
图 6是利用3″的SRTM数据(详细DTM)、15″的SRTM数据(粗糙DTM)、30″的DTM2006.0数据(参考面DTM)以及GPS数据获得的各点的RTM高程异常。在计算过程中,采用详细/粗糙DTM数据组合的目的是为了提高计算效率。随着积分半径R2的增大,计算点P的RTM高程异常值会逐步趋于稳定。在积分半径R2一定的前提下,理论上随着积分半径R1的增大,计算点P的RTM高程异常值的精度会越高,但计算效率越低。同时RTM高程异常值的变化范围越小,若给定一个可容许的变化值(如1 cm),则可从中确定积分半径R1及R2。在实际计算中本文取R1=40 km,R2=200 km。图 6结果显示,在该区域RTM高程异常在±0.05 m范围内,RTM高程异常最大值为0.042 m,最小值为-0.044 m,且东部GPS/水准点RTM高程异常变化较小,这与东部地形起伏相对较小相吻合(见图 3)。
|
| 图 6 RTM高程异常值(算例A) Fig. 6 RTM height anomaly (case A) |
表 1为采用2160阶次的EGM2008模型以及RTM数据计算得到的高程异常与GPS/水准点实测高程异常的比较结果。从表 1中可以看到,2160阶的EGM2008模型在该区域具有较高的精度,最差精度为6.0 cm,最高精度为3.1 cm。EGM2008高程异常与GPS/水准高程异常差值的平均值不为零,则暗示两者存在系统偏差。该系统偏差主要是由EGM2008模型所定义的高程基准和我国国家高程基准不一致造成的。综合EGM2008模型高程异常及RTM剩余高程异常后,GPS高程转换的精度都有不同程度的提高,4个测段高程异常精度提高量分别为5%、10%、42%和2%,说明RTM技术能提高GPS高程转换精度。
| cm | ||||
| 测段 | EGM2008(2160阶) | |||
| 最小值 | 最大值 | 平均值 | 标准差 | |
| A1 | -14.9 | -1.6 | -7.1 | 3.7 |
| A2 | -18.1 | 5.0 | -3.0 | 6.0 |
| A3 | -18.1 | -6.0 | -10.0 | 3.1 |
| A4 | -19.8 | -2.8 | -12.2 | 4.7 |
| EGM2008(2160阶)+RTM | 精度提高 | |||
| 最小值 | 最大值 | 平均值 | 标准差 | |
| -16.8 | -4.0 | -8.9 | 3.5 | 5% |
| -15.3 | 3.8 | -2.1 | 5.4 | 10% |
| -15.3 | -7.2 | -10.9 | 1.8 | 42% |
| -20.7 | -4.3 | -14.1 | 4.6 | 2% |
为了分析RTM高程异常及残余高程异常拟合技术对GPS高程转换的影响,在测段A1、A2、A3和A4中各选择3~5个GPS/水准点。选点的原则有两个:①要求每一测段中GPS/水准点平均点间距不小于25 km;②采用逐步剔除法选择最优的GPS/水准点。由于每个测段是近似直伸形式,故拟合模型采用二次曲线和三次曲线,即在每一测段都建立线路独立坐标,并忽略垂直于线路方向的高程异常变化。每一测段所选择的GPS/水准点个数及高程转换精度统计结果见表 2,高差转换精度统计结果见表 3。
| cm | |||||||||
| 拟合 方法 |
测段 | 约束GPS/水 准点个数 |
EGM2008(2160阶) | EGM2008(2160阶)+RTM | 精度 提高 |
||||
| 最小值 | 最大值 | 中误差 | 最小值 | 最大值 | 中误差 | ||||
| A1 | 4 | -6.8 | 7.1 | 4.3 | -6.7 | 6.2 | 3.5 | 19% | |
| 二次 | A2 | 3 | -4.2 | 4.8 | 2.7 | -2.3 | 3.8 | 2.2 | 20% |
| 曲线 | A3 | 3 | -7.3 | 5.2 | 3.5 | -2.0 | 2.5 | 1.0 | 71% |
| A4 | 5 | -5.6 | 5.6 | 2.1 | -4.3 | 5.1 | 1.9 | 10% | |
| A1 | 4 | -3.9 | 6.1 | 2.7 | -3.3 | 3.6 | 1.8 | 33% | |
| 三次 | A2 | 4 | -5.6 | 3.1 | 3.1 | -2.2 | 2.1 | 1.1 | 65% |
| 曲线 | A3 | 4 | -7.5 | 3.3 | 3.7 | -1.2 | 2.6 | 0.9 | 76% |
| A4 | 5 | -4.9 | 4.2 | 2.4 | -3.8 | 3.4 | 1.9 | 21% | |
从表 1和表 2可以看出:
(1) 与用EGM2008模型直接转换相比,通过对仅扣除EGM2008模型高程异常的残余高程异常进行拟合,对于二次曲线拟合,A1和A3测段精度略微降低,而A2和A4测段精度提高较大,约提高50%;对于三次曲线拟合,A3测段精度略微降低,而A1、A2和A4测段精度提高较大,除A1测段外,三次曲线拟合与二次曲线拟合精度基本相当。
(2) 通过对扣除EGM2008/RTM模型高程异常的残余高程异常进行拟合,精度能明显提高,与未顾及RTM高程异常情况相比,若选择拟合方法为二次曲线,则A1、A2、A3和A4 4个测段精度分别提高了19%、20%、71%和10%;若选择拟合方法为三次曲线,则A1、A2、A3和A4 4个测段精度分别提高了33%、65%、76%和21%;顾及RTM高程异常后,无论采用二次曲线还是三次曲线拟合方法,精度都会得到不同程度的提高,最大可提高76%。测段A4精度提高量相对较小,这和测段A4及周围地形起伏相对较小有关(见图 3),图 6结果也显示该测段RTM高程异常变化较小。
(3) 与利用EGM2008/RTM高程异常直接转换结果相比,对残余高程异常进行拟合,转换精度也获得了不同程度的提高。整体上,顾及RTM高程异常后,三次曲线拟合比二次曲线拟合精度略高,整体精度可以达到2.0 cm,在A2和A3测段,精度甚至可达到1.0 cm。
为了进一步分析本文方法获得的高差精度,将表 2中顾及RTM高程异常后的三次曲线拟合高程结果转换为高差(沿线路坐标依次求高差),并和三等、四等水准测量限差要求进行比较,结果见表 3。
表 3结果显示:除测段A1外,其余3个测段平均90%的高差满足三等水准测量精度要求。测段A1、A2和A3中所有高差均满足四等水准测量限差要求,A4测段中95%高差满足四等水准测量限差要求,经分析发现有1个GPS点高程转换精度较差,若扣除该点,则剩余高差均满足四等水准测量限差要求。
| cm | ||||||
| 拟合方法 | 测段 | 最小值 | 最大值 | 中误差 | 满足三 等比例 |
满足四 等比例 |
| 三次 曲线 |
A1 | -2.9 | 2.9 | 1.6 | 85% | 100% |
| A2 | -2.1 | 2.7 | 1.2 | 95% | 100% | |
| A3 | -2.4 | 1.9 | 1.0 | 97% | 100% | |
| A4 | -3.7 | 5.6 | 1.9 | 90% | 95% | |
算例B是某一城市GPS/水准数据,控制面积600 km2多,平均点间距约4 km,整个GPS控制区域地形起伏相对不大,但周围地形起伏很大,共有GPS/水准点41个。
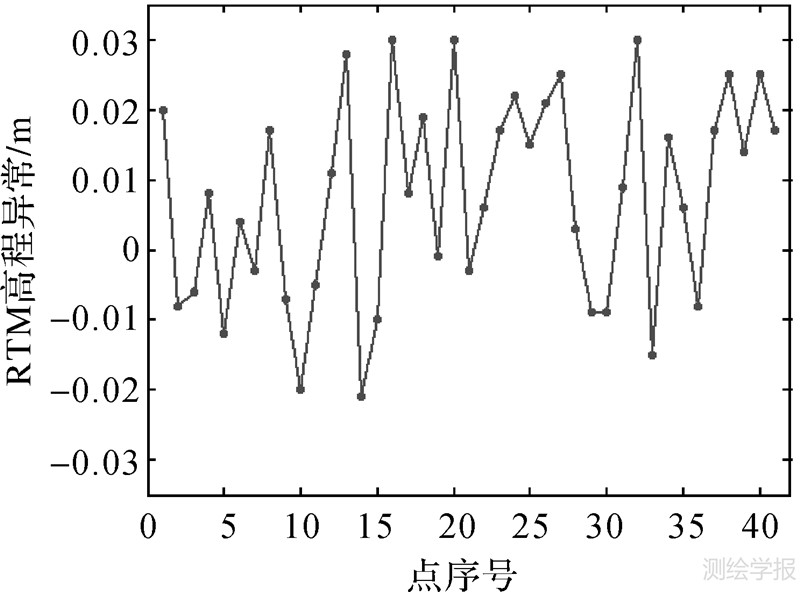
图 7是利用SRTM数据、DTM2006.0数据以及GPS数据获得的各点的RTM高程异常,计算方法同3.2节。图 7结果显示,在该区域RTM高程异常在±0.03 m范围内,RTM高程异常最大值为0.03 m,最小值为-0.021 m。
|
| 图 7 RTM高程异常值(算例B) Fig. 7 RTM height anomaly(case B) |
表 4为采用2160阶次的EGM2008模型以及RTM数据计算得到的高程异常与GPS/水准点实测高程异常的比较结果。从表 4中可以看到,2160阶的EGM2008模型在该区域精度可达2.4 cm。综合EGM2008模型高程异常及RTM剩余高程异常后,GPS高程转换的精度获得了提高,其提高量为38%,说明RTM技术能提高GPS高程转换精度。
同样对于该测区,为了分析RTM高程异常及残余高程异常拟合技术对GPS高程转换的影响。根据测区情况,选择平面和曲面函数建立残余高程异常拟合模型,采用GPS/水准点优化选择法确定已知点,个数分别为3个和6个。平面拟合和曲面拟合中约束点间距约25 km和10 km,计算结果见表 5。
表 4和表 5结果显示:与用EGM2008模型直接转换相比,仅通过对扣除EGM2008模型高程异常的残余高程异常进行拟合,则平面和曲面拟合的精度分别为2.5 cm和2.3 cm,而EGM2008模型精度为2.4 cm,精度基本相当。顾及RTM高程异常后,GPS高程转换精度显著提高,平面和曲面残余高程异常拟合方法的精度分别为1.2 cm和0.9 cm,精度分别提高了52%和61%。与利用EGM2008/ RTM模型高程异常直接转换结果相比,该方法精度可分别提高20%和40%。
| cm | ||||||||
| EGM2008(2160阶) | EGM2008(2160阶)+RTM | 精度提高 | ||||||
| 最小值 | 最大值 | 平均值 | 标准差 | 最小值 | 最大值 | 平均值 | 标准差 | |
| -20.6 | -11.7 | -15.5 | 2.4 | -18.6 | -13.4 | -16.2 | 1.5 | 38% |
| cm | ||||||||
| 拟合方法 | 约束GPS/水 准点个数 |
EGM2008(2160阶) | EGM2008(2160阶)+RTM | 精度 提高 |
||||
| 最小值 | 最大值 | 中误差 | 最小值 | 最大值 | 中误差 | |||
| 平面 | 3 | -6.2 | 3.9 | 2.5 | -2.4 | 2.2 | 1.2 | 52% |
| 曲面 | 6 | -4.4 | 3.6 | 2.3 | -1.5 | 2.3 | 0.9 | 61% |
(1) EGM2008地球重力场模型所定义的高程基准和我国国家高程基准存在系统性偏差。在局部区域,2160阶次的EGM2008地球重力场模型具有很高的精度。在算例A中,4个测段的精度从3.1~6.0 cm不等,而在算例B中精度可达到2.4 cm。
(2) 利用SRTM/DTM2006.0构建RTM数据,并将其转换为RTM高程异常,能在一定程度上对2160阶次的EGM2008模型的截断误差进行补偿。在算例A中,4个测段的精度提高量从2%~42%不等,在算例B中,精度提高约38%。
(3) 若不考虑RTM高程异常,仅通过对扣除EGM2008模型高程异常后的残余高程异常进行拟合,则能在一定程度上提高高程异常的计算精度。而通过对扣除EGM2008/RTM模型高程异常后的残余高程异常进行拟合,高程异常拟合精度明显提高。与未顾及RTM高程异常情况相比,算例A中高程精度平均提高量超过40%,高程平均精度优于2.0 cm(三次曲线拟合),而算例B中高程精度平均提高量超过50%,高程平均精度约1.0 cm。在算例A中平均90%的高差满足三等水准测量精度要求,近乎100%的高差满足四等水准测量精度要求。与利用EGM2008/ RTM模型高程异常直接转换结果相比,由该方法获得的高程异常的精度也获得了较大程度的提高,精度提高的主要原因是RTM高程异常表示高程异常中的高频部分,扣除该部分后,有利于残余高程异常的建模。
(4) 在算例A和算例B中,计算了GPS/水准点平均点间距不低于25 km的情况,为利用少量GPS/水准点进行较大范围的局部似大地水准面精化提供一种参考。本文计算所利用的数据源均可以免费获得(EGM2008模型、SRTM数据及DTM2006.0模型)。利用少量的GPS/水准点,即可获得较为满意的高程转换结果。
| [1] | PAVLIS N K, HOLMES S A, KENYON S C, et al. An Earth Gravitational Model to Degree 2160: EGM2008[R]. Vienna: EGU General Assembly 2008, 2008. |
| [2] | GRUBER T. Evaluation of the EGM2008 Gravity Field by Means of GPS Leveling and Sea Surface Topography Solutions[J]. Newton’s Bulletin, 2009(4): 3-17. |
| [3] | JEKELI C, YANH H J, KWON J H . Evaluation of EGM08—Globally and Locally in South Korea[J]. Newton’s Bulletin, 2009(4): 38-49. |
| [4] | ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289. (章传银,郭春喜,陈俊勇,等. EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报, 2009, 38(4):283-289.) |
| [5] | ZHANG Chuanyin, CHAO Dingbo, DING Jian, et al. Arithmetic and Characters Analysis of Terrain Effects for cm Order Precision Height Anomaly[J]. Acta Geodaetica et Cartographica Sinica,2006, 35(4): 308-314. (章传银,晁定波,丁剑,等.厘米级高程异常地形影响的算法及特征分析[J].测绘学报, 2006, 35(4): 308-314.) |
| [6] | HIRT C, FEATHERSTONE W E, MARTI U. Combining EGM2008 and SRTM/DTM2006.0 Residual Terrain Model Data to Improve Quasigeoid Computations in Mountainous Areas Devoid of Gravity Data[J]. Journal of Geodesy, 2010, 84(9): 557-567. |
| [7] | HIRT C. Prediction of Vertical Deflections from High-degree Spherical Harmonic Synthesis and Residual Terrain Model Data[J]. Journal of Geodesy, 2010, 84(3): 179-190. |
| [8] | HIRT C, MARTI U, BüRKI B. Assessment of EGM2008 in Europe Using Accurate Astrogeodetic Vertical Deflections and Omission Error Estimates from SRTM/DTM2006.0 Residual Terrain Model Data[J]. Journal of Geophysical Research, 2010, 115(B10404): 1-13. |
| [9] | FORSBERG R, TSCHERNING C C. The Use of Height Data in Gravity Field Approximation by Collocation[J]. Journal of Geophysical Research, 1981, 86(B9): 7843-7854. |
| [10] | FORSBERG R. A study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling[R]. Report 355. Columbus: Ohio State University, 1984. |
| [11] | FORSBERG R. Terrain Effects in Geoid Computations[R]. Copenhagen: National Survey and Cadastre,1994. |
| [12] | HOLMES S A, FEATHERSTONE W E. A Unified Approach to the Clenshaw Summation and the Recursive Computation of Very High Degree and Order Normalised Associated Legendre Functions[J]. Journal of Geodesy, 2002, 76(5): 279-299. |
| [13] | NAGY D, PAPP G, BENEDEK J. The Gravitational Potential and Its Derivatives for the Prism[J]. Journal of Geodesy, 2000, 74(7-8): 552-560. |
| [14] | NAGY D, PAPP G, BENEDEK J. Corrections to “The Gravitational Potential and Its Derivatives for the Prism”[J]. Journal of Geodesy, 2002, 76(8): 475. |
| [15] | PAVLIS N K, FACTOR J K, HOLMES S A. Terrain-related Gravimetric Quantities Computed for the Next EGM[C]//Proceedings of the 1st International Symposium of the International Gravity Field Service: 18. Istanbul: [s.n.], 2007: 318-323. |
| [16] | SHEN Yunzhong, GAO Dakai, ZHANG Xingfu. Optimal Choice of GPS Leveling Points[J]. Geotechnical Investigation & Surveying, 2004(6): 49-51. (沈云中,高达凯,张兴福. GPS水准点优化选择法[J].工程勘察, 2004(6): 49-51.) |