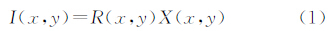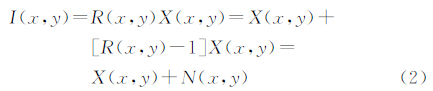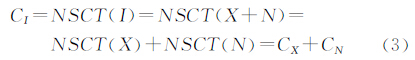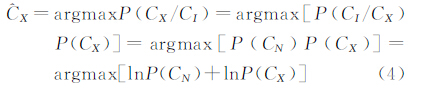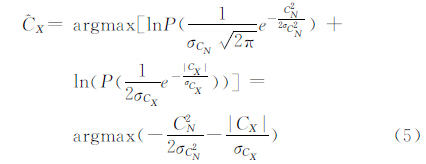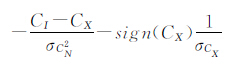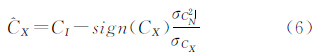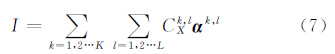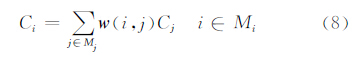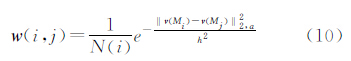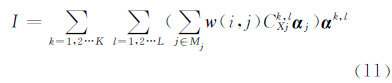1 引 言
合成孔径雷达(synthetic aperture radar，SAR)图像是由接收散射回波信号的相干获得的，因此会产生随机散布的相干斑(speckle)，降低了目标探测和解译的能力，增加了图像处理的难度。传统的SAR图像去噪方法如增强Lee滤波[1]、Gamma-MAP滤波[2]等主要利用图像空域的统计特征。由于对图像局部区域的假设有时与实际情况不完全相符，所以在去噪的同时不能较好地保留边缘和纹理细节。因而只通过对图像域的灰度信息进行统计建模不能充分体现SAR图像多尺度多分辨等特性，对SAR图像去噪是远远不够的[3]。基于小波域统计特性的方法[4]在多尺度多分辨的统计模型下分析相干斑噪声分布特性，能够保持图像的细节以及轮廓特征。然而小波基只对于具有点状奇异性的目标函数是最优基，小波系数是稀疏的，对于具有线状奇异的函数，小波系数则不再稀疏[5]。多尺度几何分析(multiscale geometric analysis,MGA)方法是继小波变换之后，提出的又一类新的图像表示方法[6]，能够在保持小波分析优良的时(空)频局部化特性的同时，通过构造具有各向异性的基来检测小波所不能充分刻画的几何结构，很好地保持图像的奇异性信息，从而有利于图像去噪质量的提高[7]。
轮廓波变换(contourlet transform,CT)[8]变换是一种MGA方法，在 SAR图像去噪中也得到成功应用[3]，但由于其缺乏平移不变性，因此在采取收缩法去噪时会引入Gibbs噪声[6]。文献[9]在轮廓波变换的基础上采用非下采样金字塔分解和非下采样方向滤波器组(directional filter banks,DFB)分解，提出了非下采样轮廓波变换(nonsubsampled contourlet transform，NSCT)。它是一种新的具有完全平移不变性的MGA方法，已在SAR图像去噪处理中显示出其优势[7, 10, 11, 12]。由于非下采样变换域去噪方法比下采样变换域去噪方法提供了更加丰富、冗余的图像细节信息，而且具有平移不变性，所以前者的性能一般高于后者[7]。但是目前基于NSCT的方法由于阈值收缩，会产生“裂痕”噪声，并且大多适用于机载SAR影像，对星载SAR数据处理效果还不是很理想。
笔者根据SAR图像数据的特征，引入了非对数加性模型，并在该模型下对SAR图像NSCT域中的噪声分布统计建模，应用最大后验(MAP)准则和在NSCT域中的5851约束相结合的方法解求SAR图像真实信号的NSCT系数，避免了裂痕噪声，增强了滤波视觉效果。最后使用本文方法与传统NSCT去噪方法和目前主流去噪方法对真实星载SAR图像进行去噪试验，证明了本文方法的有效性。
2 SAR图像的非对数加性相干斑模型SAR图像相干斑模型先验信息对SAR图像噪声抑制具有重要意义。在图像域，完全发育的相干斑噪声模型可以表示为
式中，(x,y)为图像坐标;I为观测的SAR图像强度；X为真实后向散射强度；R为产生相干斑噪声的过程，是一个均值为1，方差与等效视数成反比，服从Γ分布的二阶随机过程。R和X是两个相互独立的随机过程。
在乘性噪声模型下，通常去噪的思路是首先对图像进行对数变换，使图像转换为加性模型，假设加性对数噪声为零均值高斯白噪声进行去噪。但是这样处理不能很好地保持原图像的辐射特性，变换后的相干斑噪声并不是零均值的，这会使去噪后的结果图像的均值偏离原始图像的均值，图像在视觉上会变暗[13]。同时对数模型计算的时间代价也非常大。
因此，对引入SAR图像非对数加性模型[14]，乘性模型式(1)改写为
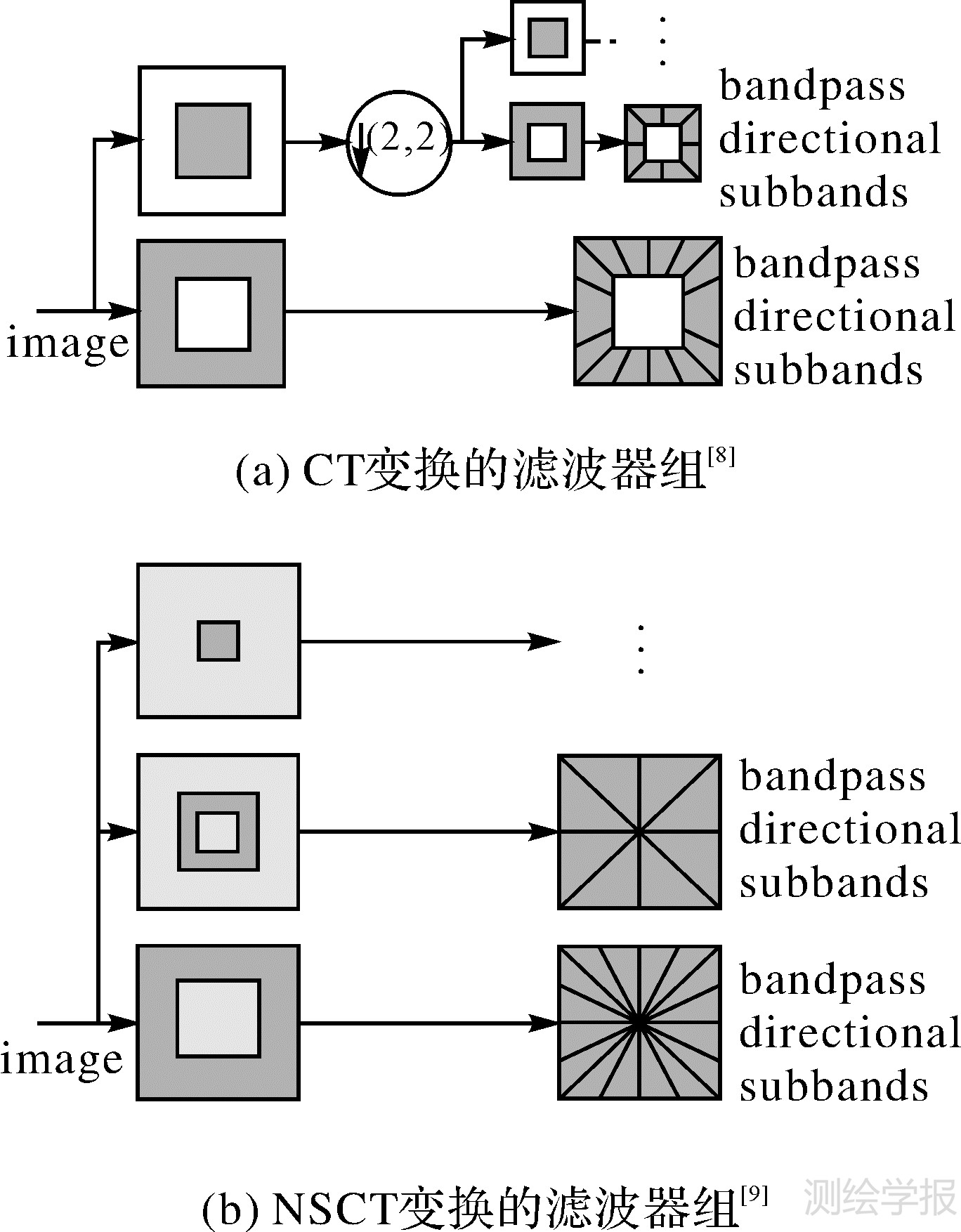
N(x,y)=[R(x,y)－1]X(x,y)可认为是和实际真实反射强度X(x,y)相关的噪声。文献[10]证明了平稳区域噪声N(x,y)的NSCT系数符合零均值高斯分布。 3 非下采样轮廓波变换
轮廓波变换是一种图像多尺度几何表示方法[8]。由拉普拉斯塔式分解 (Laplacian pyramid,LP)和方向滤波器组(DFB)滤波两部分实现。先由LP把原始图像分解为低频子带和高频子带，然后高频子带经过DFB分解为多个方向子带。对低频子带重复上述过程即实现了对原始图像的多分辨率、多方向分解。图 1(a)为CT变换的滤波器组结构。CT变换具有良好的各向异性，基的支撑区间是长宽比随尺度变换的“长方形”结构，能够沿图像中的轮廓边缘用最少的系数来逼近奇异曲线。但是由于下采样机制，在 LP分解时，对图像进行了隔行隔列下采样，这在较大程度地降低变换冗余性的同时导致了 CT变换不具有平移不变性，限制了其在一些图像处理领域里的应用。
因此，文献[9]又提出了NSCT变换，保留了CT变换的频率分割结构,去掉原CT变换中的下采样步骤，采用非下采样塔式分解(NSPL)和构造非下采样滤波器组(NSDFB)。图 1(b)为NSCT变换的滤波器组结构。NSCT具有更加丰富的基函数集，提供了更好的频率选择性和正则性，有利于更好地捕捉图像中的细节信息，同时保证了平移不变性。
|
| 图 1 Fig. 1 |
图像中的特征一般具有方向性，经过NSCT变换后，具有方向性的空间域的图像特征只分布在少数几个子带的NSCT系数上。而噪声一般不具有方向性，经过NSCT变换后会均匀分布在所有方向子带。因而可以在NSCT域对对图像统计建模，去噪处理。
4.1 SAR图像NSCT域MAP多层阈值估计[10]对SAR图像的一条子带的NSCT变换在非对数加性模型下可以表示为
式中，CI、CX、CN分别为观测图像、真实反射强度、噪声的NSCT系数；NSCT(·)为NSCT变换过程。
图像可看成是由各个很小的同质区域组成[15]，文献[16]指出在同质区域内的地物真实后向散射强度是一个常数，这种小的同质区域的极限情况就是单个像素为一同质区域。与图像空域同质区域相对应的是NSCT域高频子带中的平稳区域，文献[10]证明了在NSCT域高频子带中的平稳区域CX、CN分别可用零均值的高斯分布和零均值的Laplace分布建模。CX的估计值ĈX根据最大后验(MAP)准则由CX和CI计算得到
式中，P(CI)、P(CX)、P(CN)分别为CI、CX、CN的概率密度函数。式(4)可以表示为 上式对CX求导可得 令其等于0，求得
由文献[10]可知sign(CX)与sign(CI)相同，由文献[11]可确定sign(CI )σCN2 σCX 。设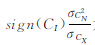
为阈值对NSCT域各条高频子带中的平稳区域进行软阈值去噪。为了下面对全部系数NL优化，保持系数的独立性，在实际计算中，取极端情况，每个NSCT系数看做一个平稳区域。
对于各个子带分别软阈值去噪后重建的结果存在着裂痕噪声，并由于阈值法对系数的“过扼杀”[6]，导致图像在边缘处出现模糊。
实际上，某些NSCT系数只含有噪声，而某些NSCT系数则都为有效信号，对某一子带采用一个单一的模型建模，设置同一阈值进行收缩，必然会造成去噪不彻底或图像失真。图像经NSCT由各向异性的基分解后，信号的几何结构得到了充分保留，实际信号会表现为很强的相关性，噪声因为是随机分布的表现为弱相关或者不相关[17]。因而可以根据NSCT分解后系数的相关性对图像进行去噪后的优化处理。
在实际计算中，每个NSCT系数不仅与同子带系数之间具有相关性，同时不同子带和上下层子带之间与同一空间位置对应的NSCT系数由于表示同一信号不同层次不同方向的分解，也具有相关性。在同一空间位置的所有NSCT系数的关系可以表示为
式中，CXk,l为在空间X位置上k层l子带的NSCT系数；αk,l∈Ψ为张成空间I的NSCT基； K、L分别为分解的层数和每层分解的子带数。
文献[18]中提出的NL滤波方法在对某一信号滤波时同时考虑了本区域以及相关邻域的关系，能够考虑到与该信号相似信号对其的影响。对于软阈值收缩后的各子带的NSCT某一系数Ci，其与同子带其他系数具有一定相关性，借鉴文[18]的方法，有
式中，Mi和Mj分别是包含Ci和Cj的两个区域；权值w(i,j)由Mi与Mj的相似程度决定。由于NSCT的基是各项异性的，所以直接使用NSCT系数不能很好的表示他们之间关系。加入NSCT基α，式(8)可以写为 令v(Mi)、v(Mj)分别是Mi和Mj的系数向量，可得 式中，‖v(Mi)－v(Mj)‖2,a2为一个加权欧式距离递减函数，a>0为高斯核的标准差；N(i)=
为正则化系数；h为滤波尺度系数。
由式(7)和式(9)可得
对每一子带NSCT系数均作NL滤波，对于表示实际信号的系数，与其具有相关性的系数会提供支持，而噪声则会进一步削弱。
5 算法实现步骤1：设置NSCT变换分解层数以及各子带方向数。对输入SAR图像进行NSCT变换，得到NSCT系数。
步骤2：基于MAP的 BayesShrink 阈值估计，根据文中3.1所述方法分层计算每一个子带的收缩阈值，分层多阈值对各个子带软阈值收缩去噪。
步骤3：对各子带软阈值收缩后的结果，根据4.2中所述方法作non-local平滑约束。
步骤4：对去噪后的NSCT系数做NSCT逆变换，得到最终的去噪图像。 6 试验及评价
本文采用两组星载SAR图像数据验证所提出去噪方法的有效性。第一组为TerraSAR-X的SSC图像(256×256)，主要验证本方法对人工地物和水体的去噪效果；第二组为Cosmo-SkyMed的SCS图像(256×256)，主要验证本方法对田地的去噪效果。试验中采用了增强Lee[1]、BM3D[19]、PPB[20]、基于最大后验的NSCT[10]和本文方法作对比试验。
试验中，增强Lee滤波采用3×3窗口，BM3D滤波采用文献[19]的方法，PPB滤波采用文献[20]方法迭代25次，基于最大后验的NSCT滤波采用文献[10]的方法，基于最大后验的NSCT和本文方法中NSCT变换选择“max flat”NSPL分解和“dmax flat7” NSDFB滤波器组，为了能够较好的保存图像的细节，NSCT作4层分解，方向数为 4、8、16、16 。试验结果见图 2、图 3。
|
| 图 2 TerraSAR-X图像去噪结果 Fig. 2 The denoising result of TerraSAR-X image |
|
| 图 3 Cosmo-SkyMed图像去噪结果 Fig. 3 The denoising result of Cosmo-SkyMed image |
SAR图像的相干斑抑制过程是盲的恢复过程，PSNR(peak signal to noise ratio)等不能用来评价去噪结果[3]。本文采用等效视数(equivalent number of looks ，ENL)、比值图像均值[10]，作为去噪结果客观的评价指标，PSNR反映了滤波后图像与原始图像之间的差异，用来评价滤波图像分辨率的变化和损失。试验数据的试验结果见表 1、表 2。
| 滤波方法 | ENL | 比值图像均值 | PSNR |
| 原始图像 | 6.795 1 | ||
| 增强Lee | 13.776 5 | 0.991 7 | 18.238 6 |
| BM3D | 10.545 9 | 0.985 6 | 21.872 6 |
| PPB | 17.594 7 | 1.090 1 | 16.999 9 |
| NSCT | 10.759 8 | 0.977 8 | 24.000 0 |
| 本文方法 | 21.335 2 | 1.003 3 | 17.344 5 |
| 滤波方法 | ENL | 比值图像均值 | PSNR |
| 原始图像 | 6.6796 | ||
| 增强Lee | 15.8547 | 0.9912 | 12.1619 |
| BM3D | 10.9126 | 0.9794 | 22.1858 |
| PPB | 22.0518 | 1.0661 | 16.2621 |
| NSCT | 17.7426 | 0.9776 | 23.5259 |
| 本文方法 | 31.6262 | 1.0031 | 16.0156 |
等效视数用来衡量一幅图像斑点噪声相对强度，目前被广泛接受为SAR相干斑抑制的指标。等效视数越大，去噪效果越好。本文方法去噪结果的等效视数高于其他方法，这与目视效果一致。在理想情况下，原始图像与去噪后结果图像的比值图像为相干斑噪声图像。 而相干斑噪声图像的均值为1。所以比值图像的均值越接近1 ，去噪结果越好，对原始图像辐射特性保持得越好。本文方法对应的比值图像的均值最接近1，说明对原始图像辐射特性保持最好。PSNR反映了滤波结果与原始图像之间的差异，PSNR值越大则与原始图像差异越小，因为去噪的同时牺牲了图像的细节和分辨率，所以要辩证地看待PSNR值。本文方法PSNR值与增强Lee和PPB方法接近，即在分辨率和细节保持上与一些经典方法相近，而PSNR值低于某些方法的同时，去噪效果也优于这些方法。
从主观上评价，在两组试验数据中，本文方法对水体和平坦地区的去噪结果明显优于其他方法，在同质区域产生的伪吉布斯效应是最弱的，同时具有较强的细节保持能力，并且改善了基于最大后验的NSCT去噪方法在某些局部区域会产生划痕的缺点。由基于最大后验的NSCT滤波方法和本文方法的结果相比较可以看出，虽然本文方法结果更加平滑，但由于NL约束的引入，计算过程中NSCT系数多作了一次平滑处理，所以对结果的细节纹理保持产生了一定的影响。 7 结 论
本文针对SAR图像对数加性模型不能够很好保持原图像的辐射特性和计算时间代价大的问题引入了非对数加性模型。基于文献[9]提出的方法，利用NSCT对SAR图像细节信息的刻画能力[12]对SAR图像作NSCT分解。然后对SAR图像同质区域在非对数加性模型下的噪声分布应用高斯分布建模，并基于MAP准则计算每个高频子带中真实信号NSCT系数的阈值，分层多阈值去噪。针对频域阈值去噪对真实信号“过扼杀”的问题，考虑到在频域真实信号NSCT之间的相关性，借鉴NL理论，对每个子带阈值去噪的结果进行NL滤波，进一步增强真实信号的NSCT系数，削弱残存噪声的影响。
通过试验，与经典的增强Lee滤波算法和目前效果较好的PPB去噪方法等相比，在客观指标上本文方法在原图像辐射特性保持和去噪效果上均优于其他方法，在主观目视效果上，在SAR图像的同质区域去噪效果明显，纹理结构和细节也得到有效保持。
但是从试验中也可以看到，由于NL方法的引入，在解决了传统的NSCT阈值去噪方法产生裂痕噪声和边缘模糊的同时，即使在同质区域噪声去除效果良好，算法的计算时间代价要小于PPB方法，图像某些细节部分不如PPB方法清晰。因此对去噪后图像细节纹理的保持增强还需作进一步的研究。
| [1] | LEE J S.Digital Image Enhancement and Noise Filtering by Use of Local Statistics[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1980,PAMI-2(2):165-168. |
| [2] | LOPES A,NEZRY E,TOUZI R,et al.Maximum a Posteriori Filtering and First Order Texture Models in SAR Images[C]//Proceedings of IGARSS'90.Washington,D C:IEEE,1990:2409-2412. |
| [3] | SHA Yuheng,CONG Lin,SUN Qiang,et al.SAR Image Despeckling Based on Contourlet Domain Hidden Markov Trees Model[J].Journal Infrared Millim Waves,2009,28(1):66-71.(沙宇恒,丛琳,孙强,等.基于Contourlet域HMT模型的SAR图像相干斑抑制[J].红外与毫米波学报,2009,28(1):66-71.) |
| [4] | ZHANG Jun,LIU Jian.A Speckle Reduction Algorithm by Soft-thresholding Based on Wavelet Filters for SAR Images[J].Acta Geodaetica et Cartographica Sinica,1998,27(2):119-124.(张俊,柳健.SAR图像斑点噪声的小波软门限滤除算法[J].测绘学报,1998,27(2):119-124.) |
| [5] | JIAO Licheng,TAN Shan.Development and Prospect of Image Multiscale Geometric Analysis[J].Acta Electronica Sinica,2003,31(12A):43-50.(焦李成,谭山.图像多尺度几何分析:回顾和展望.电子学报,2003,31(12A):43-50.) |
| [6] | DENG Chengzhi.Research on Image Sparse Representation Theory and Its Applications[D].Wuhan:Huazhong University of Science and Technology,2008.(邓承志.图像稀疏表示理论及其应用[D].武汉:华中科技大学,2008.) |
| [7] | SUN Qiang,GAO Yong,JIAO Licheng.Image Denoising Based on Spatially Adaptive Bayesian Shrinkage in NSCT Domain[J].Journal of Computer Applications,2010,30(8):2080-2084.(孙强,高勇,焦李成.基于空间自适应Bayesian缩减的NSCT域图像去噪方法[J].计算机应用,2010,30(8):2080-2084.) |
| [8] | DO M N,VETTERLI M.The Contourlet Transform:An Efficient Directional Multiresolution Image Representation[J].IEEE Transaction on Image Processing,2005,14(12):2091-2106. |
| [9] | CUNHA A L,ZHOU Jianping,DO M N.The Nonsubsampled Contourlet Transform:Theory,Design,and Applications[J].IEEE Transaction on Image Processing,2006,15(10):3089-3101. |
| [10] | FENG Hongxiao,HOU Biao,JIAO Licheng,et al.SAR Image Despeckling Based on Local Gaussian Model and MAP in NSCT Domain[J].Acta Electronica Sinica,2010,38(4):811-816.(凤宏晓,侯彪,焦李成,等.基于非下采样Contourlet域局部高斯模型和MAP的SAR图像相干斑抑制[J].电子学报,2010,38(4):811-816.) |
| [11] | YANG Xiaohui,JIAO Licheng,NIU Hongjuan,et al.Image Denoising Method for Nonsubsampled Contourlet Based on Multi-threshold[J].Computer Engineering,2010,36(4):200-204.(杨晓慧,焦李成,牛宏娟,等.基于多阈值的非下采样轮廓波图像去噪方法[J].计算机工程,2010,36(4):200-204.) |
| [12] | CHANG Xia,JIAO Licheng,LIU Fang,et al.SAR Image Despeckling Based on the Estimation of Speckle Variance in Nonsubsampled Contourlet Domain[J].Acta Electronica Sinica,2010,38(6):1328-1333.(常霞,焦李成,刘芳,等.基于斑点方差估计的非下采样Contourlet域SAR图像去噪[J].电子学报,2010,38(6):1328-1333.) |
| [13] | XIE H,PIERCE L E,ULABY F T.Statistical Properties of Logarithmically Transformed Speckle[J].IEEE Transactions on Geoscience and Remote Sensing,2002,40(3):721-727. |
| [14] | ARGENTI F,ALPARONE L.Speckle Removal from SAR Images in the Undecimated Wavelet Domain[J].IEEE Transactions on Geoscience and Remote Sensing,2002,40(11):2363-2374. |
| [15] | LEE J S,HOPPEL K,MANGO S.Unsupervised Estimation of Speckle Noise in Radar Images[J].International Journal of Imaging Systems and Technology,1992,4(4):298-305. |
| [16] | LOPES A,TOUZI R,NEZRY E.Adaptive Speckle Filters and Scene Heterogeneity[J].IEEE Transactions Geoscience and Remote Sensing,1990,28(6):992-1000. |
| [17] | ZHANG Xuemeng,JI Fang.The Study of Image Denoising Based on the Wavelet Coefficients Relevance[J].Journal of Weifang Educational College,2010,23(2):90-91.(张学梦,籍芳.基于小波系数相关性的图像去噪研究[J].潍坊教育学院学报,2010,23(2):90-91.) |
| [18] | BUADES A,COLL B,MOREL J M.A Non-local Algorithm for Image Denoising[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition:2.Palma de Mallorca:IEEE,2005:60-65. |
| [19] | DABOV K,FOI A,KATKOVNIK V,et al.Image Denoising by Sparse 3D Transform-domain Collaborative Filtering[J].IEEE Transactions on Image Processing,2007,16(8):2080-2095. |
| [20] | DELEDALLE C A,DENIS L,TUPIN F.Iterative Weighted Maximum Likelihood Denoising with Probabilistic Patch-based Weights[J].IEEE Transactions on Image Processing,2009,18(12):2661-2672. |