2.中国科学院研究生院,北京 100049;
3.航天飞行动力学技术重点实验室,北京 100094
2.Graduate University of Chinese Academy of Sciences,Beijing 100049, China;
3.Science and Technology on Aerospace Flight dynamics Laboratory,Beijing 100094, China
1 引言
卫星激光测距(SLR)是一种重要的现代空间大地测量技术,其观测资料被用来精确测定卫星轨道、地心运动、地球自转、地球重力场等,在地球科学、空间环境和基本物理研究方面取得了丰硕成果[1, 2, 3]。在参与建立国际地球参考架(ITRF)的过程中,SLR被作为定义坐标原点的重要的甚至是唯一的手段,在尺度因子确定方面也持续发挥着重要作用[4]。近年来,SLR的几项关键技术取得了巨大进步:超短激光脉冲技术和皮秒计时器的应用提高了测距精度,白天测距大大增加了观测数据量,高重复频率(千赫兹)测距的实现更使得观测数量和精度都有了大幅度提高[3]。新增测站进一步改善了SLR全球观测网的几何分布,并且保持着良好的观测精度[5]。现在,全球SLR观测系统单次测距精度已经达到或接近毫米级[6]。
在利用SLR数据进行卫星精密定轨过程中,需要高精度的测量模型来进行星地距离归算修正,质心改正就是测量模型中不可忽略的一个因素。从SLR实测的激光脉冲往返时间间隔换算得到的是地面测站与卫星表面激光反射点之间的距离,而在计算卫星精密星历、确定地球参考架或其他SLR数据应用中通常要用到卫星质心与测站之间的距离。因此,必须在实测距离中加入卫星有效反射面至卫星质心的距离补偿改正,这就是卫星的质心改正。卫星质心改正与星载角反射器的尺度、几何构型、制作材料和阵列分布有关,可以通过相关的理论计算和卫星发射前的地面光学检验等手段确定[7, 8]。
在现有的SLR精密定轨软件中,对某一特定的卫星一般采用全球各测站统一的质心改正值[9]。然而,目前SLR测量精度正在迈向毫米级,各种科学应用也对SLR数据分析与评估提出更高要求,因此有必要分析卫星质心改正对测站系统运行模式依赖性的影响。与测站出射激光脉冲相比,经过星载角反射器阵列反射的激光脉冲不仅被展宽,而且脉冲轮廓发生改变,这就是“卫星形状效应”[10]。数值模拟和理论模型分析表明,卫星形状效应将给激光卫星的观测数据带来至少几毫米的偏差[10, 11, 12]。在不考虑地球大气的影响下,这一效应导致卫星质心改正主要与以下3类因素有关:① 地面发射系统的出射激光波长、出射脉冲能量与波形,这类因素决定了发射光束中光子在时间和空间上的分布;② 星载角反射器阵列的光学特性与几何分布,这类因素确定了发射光束中同一波阵面的光子被反射器阵列中不同反射器反射的时间差,即确定了脉冲波形的展宽程度,再结合第一类因素,可以确定返回激光脉冲中光子能量在时间上的分布;③ 地面接收系统探测器的光电响应特性,这类因素确定了回波光子从到达探测器到转化为光电流而被记录的时间。3类因素的综合确定了激光脉冲往返时间的修正值,最终可换算得到卫星质心改正。
为实现高精度SLR定轨,以及保障各种SLR科学应用和高精度ITRF构建的需求,有必要分析卫星形状效应的影响程度。这意味着在高精度的SLR数据处理中不应继续采用全球统一的质心改正标称值,而应对不同测站的质心改正加以仔细考虑[13]。鉴于不同测站卫星质心不同改正对利用SLR资料精密确定ITRF尺度因子的重要性,不断提高这一改正的精度也已被国际激光测距服务组织(ILRS)列为其信号处理工作组的首要任务之一[14]。在此背景下,笔者利用SLR实测数据,分析不同测站卫星质心不同改正对精密定轨水平的影响。 2 定轨策略
本文选择Lageos-1/2和Etalon-1/2共4颗卫星作为研究对象。它们处于中高轨道,是专用测地卫星,被ILRS列为优先观测目标[15]。这些卫星定轨方案比较明确,不确定因素少,易于实现高精度动力学短弧定轨[16, 17]。利用上海天文台SHORDE软件,遵照轨道统计学原理[18],对上述卫星进行精密定轨,所采用的模型和参数如表 1所示。
| Lageos-1/2 | Etalon-1/2 | |
| 参考架和测量模型 | ||
| 地球参考架 | ITRF2000 | |
| 岁差模型 | IAU1976 | |
| 章动模型 | IAU1980+IERS章动改正 | |
| 大气折射改正 | Marini-Murray模型 | |
| 原质心改正/m | 0.251,全球统一 | 0.576,全球统一 |
| 现质心改正/m | 0.245~0.254
(参见表2) |
0.565~0.610
|
| 力学模型 | ||
| 地球重力场/阶 | GGM001C,
30×30 |
GGM001C,
15×15 |
| 固体潮摄动 | Wahr模型 | |
| 海潮摄动 | CSR3.0 | |
| 行星摄动 | JPL DE403 | |
| 数值积分 | ||
| 积分步长/s | 150 | 300 |
| 定轨弧长/d | 3 | 7 |
| 估计参数/d | 3 | 7 |
| 收敛准则/m | 0.001 | 0.01 |
测站坐标采用ITRF2000,对观测量进行潮汐改正(固体潮、极潮、海潮负荷形变造成的台站位移改正)、对流层折射改正、广义相对论引力时延改正和卫星质心改正。
全球统一的卫星质心改正以下称为“原质心改正”,不同测站卫星质心不同改正以下称为“现质心改正”。Lageos-1和Lageos-2相似,原质心改正为0.251m[7],而各测站的现质心改正为0.245~0.254m,最大相差9mm;Etalon-1和Etalon-2相似,原质心改正为0.576m[8],各测站的现质心改正为0.565~0.610m,最大差别超过4cm。这4颗卫星的现质心改正如表 2所示,是通过对星载角反射器和地面发射与接收系统特性的分析确定的,由ILRS信号处理工作组提供[14]。
| 现质心改正/mm | |||
| 测站代号和名称 | Lageos-1/2 | Etalon-1/2 | |
| 1873 | Simeiz | 246 | 598 |
| 1879 | Altay | 251 | 605 |
| 1884 | Riga | 250 | 607 |
| 7080 | McDonald | 249 | 603 |
| 7090 | Yarragadee | 249 | 603 |
| 7105 | Greenbelt | 249 | 603 |
| 7110 | Mon. Peak | 249 | 603 |
| 7119 | Haleakala | 249 | 603 |
| 7124 | Tahiti | 249 | 603 |
| 7237 | Changchun | 248 | 575 |
| 7249 | Beijing | 251 | 575 |
| 7355 | Urumqi | 251 | 581 |
| 7358 | Tanegashima | 250 | 607 |
| 7405 | Concepcion | 246 | 575 |
| 7406 | San Juan | 250 | 581 |
| 7501 | Hartebeesthoek | 247 | 603 |
| 7806 | Metsahovi | 251 | 607 |
| 7810 | Zimmerwald | 248 | 572 |
| 7811 | Borowiec | 253 | 607 |
| 7824 | San Fernando | 249 | 578 |
| 7825 | Stromlo | 252 | 581 |
| 7832 | Riyadh | 249 | 578 |
| 7835 | Grasse | 250 | 609 |
| 7836 | Potsdam | 254 | 609 |
| 7838 | Simosato | 250 | 607 |
| 7839 | Graz | 252 | 574 |
| 7840 | Herstmonceux | 245 | 565 |
| 7841 | Potsdam3 | 251 | 609 |
| 7941 | Matera | 250 | 610 |
| 8834 | Wettzell | 250 | 608 |
| 注:现质心改正参考文献[14] | |||
考虑的摄动力包括:地球非球形部分的引力(主要包括地球重力场摄动、固体潮摄动、海潮摄动、地球自转形变附加摄动)、日月引力、行星摄动、广义相对论改正、类阻力摄动、太阳辐射压摄动、地球红外辐射和反照压力及经验力。由于Lageos和Etalon的卫星高度不一样,Lageos-1/2轨道高度约6000km,其类阻力摄动需要估计,而Etalon-1/2轨道高度约19000km,轨道较高,类阻力摄动可不估计。轨道高度的差别导致地球重力场截断阶数也有所不同,Lageos-1/2采用30×30阶,而Etalon-1/2采用15×15阶。同时,由于轨道高度不同,在综合考虑截断误差和累积误差影响后,选取Lageos-1/2数值积分步长为150s,而Etalon-1/2数值积分步长为300s。由于Lageos-1/2观测数据量大,定轨精度高,因此选取1mm作为它的收敛标准,每3d解算一组动力学参数,而更高轨道的Etalon-1/2数据量明显偏少,精密定轨过程不甚稳定,收敛判据可略作放松,选1cm作为它的收敛标准,解算参数的弧长延长至7d一组。 2.3 解算参数
在动力学定轨过程中,为有效吸收力学模型、测量模型以及观测数据中的误差,在解算卫星轨道参数时,将部分运动学参数和动力学参数作为待估量一起解算。为保证观测法方程求解精度,又要使各待估参数之间的相关性尽量减弱。这4颗卫星的待估参数包括类阻力系数、横向和法向经验加速度、太阳辐射压系数和地球自转参数。 3 结果与分析
根据上述方案,利用这4颗卫星近3年的SLR数据进行短弧精密定轨。
对Lageos-1从2008-01-01—2010-12-30,共365个3d弧段分别应用原质心改正和现质心改正进行定轨,结果如图 1所示。Lageos-2与之类似,结果如图 2所示。可以看出:① Lageos-1/2的3d短弧定轨精度(加权中误差WRMS)一般都在1~2cm,最差精度不大于3cm;② 采用现质心改正后,定轨精度有普遍提高,最大提高量分别达到1.38mm(Lageos-1)和4.61mm(Lageos-2)。虽然平均提高幅度有限,分别只有0.42mm(Lageos-1)和0.36mm(Lageos-2),但分别有94.0%(Lageos-1)和91.8%(Lageos-2)的弧段精度得到提高,可见提高确实是普遍的,是系统性的,如表 3第2列和第3列所示。
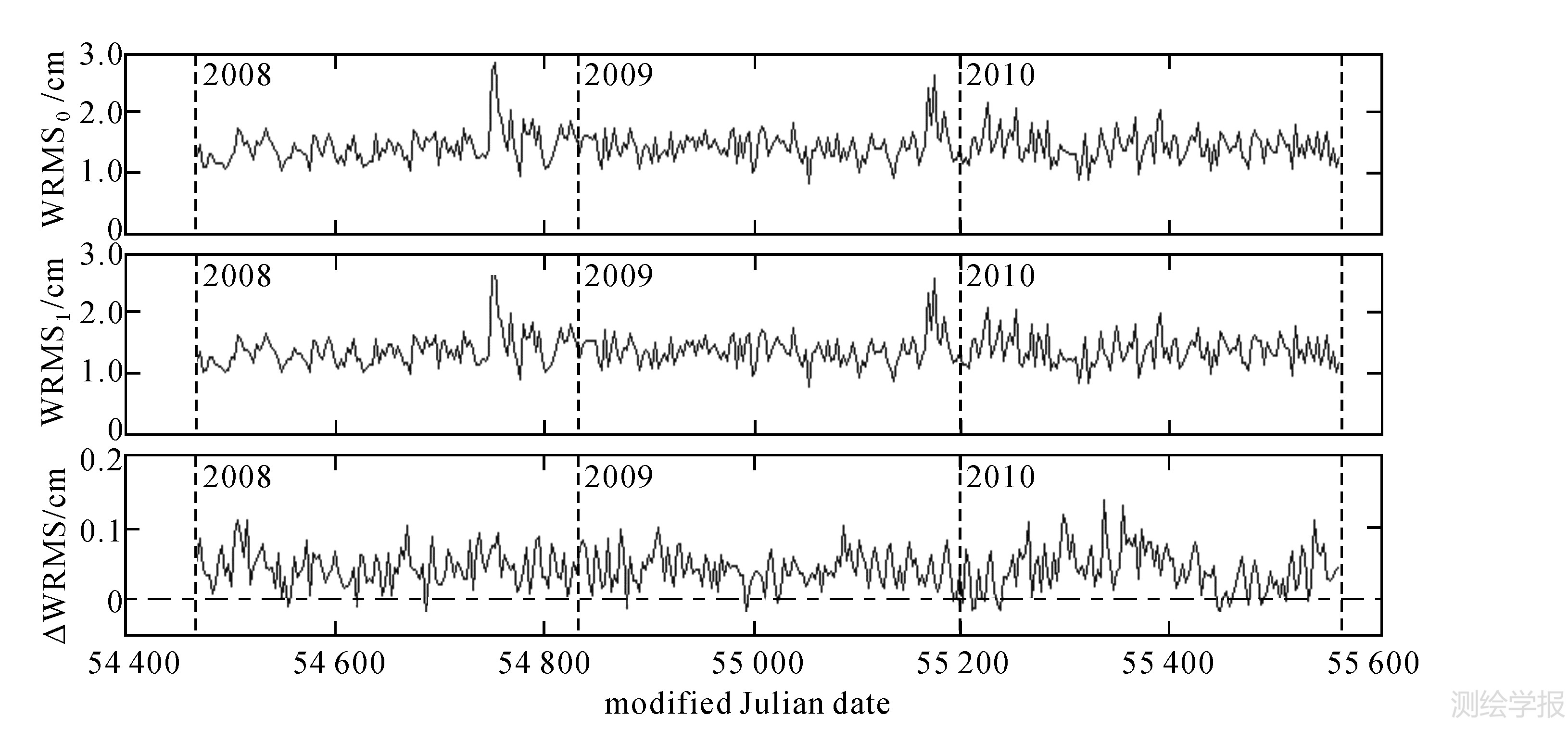
|
| 图 1 对Lageos-1,采用原质心改正时的定轨精度(上),采用现质心改正后的定轨精度(中),以及二者之差,即定轨精度提高量(下) Fig. 1 Precision of orbit determination for Lageos-1 by adopting global uniform CoM correction (top panel) and system-dependent CoM correction(middle panel), respectively. The bottom panel showed the difference between above two, i.e. the improvement of precision |
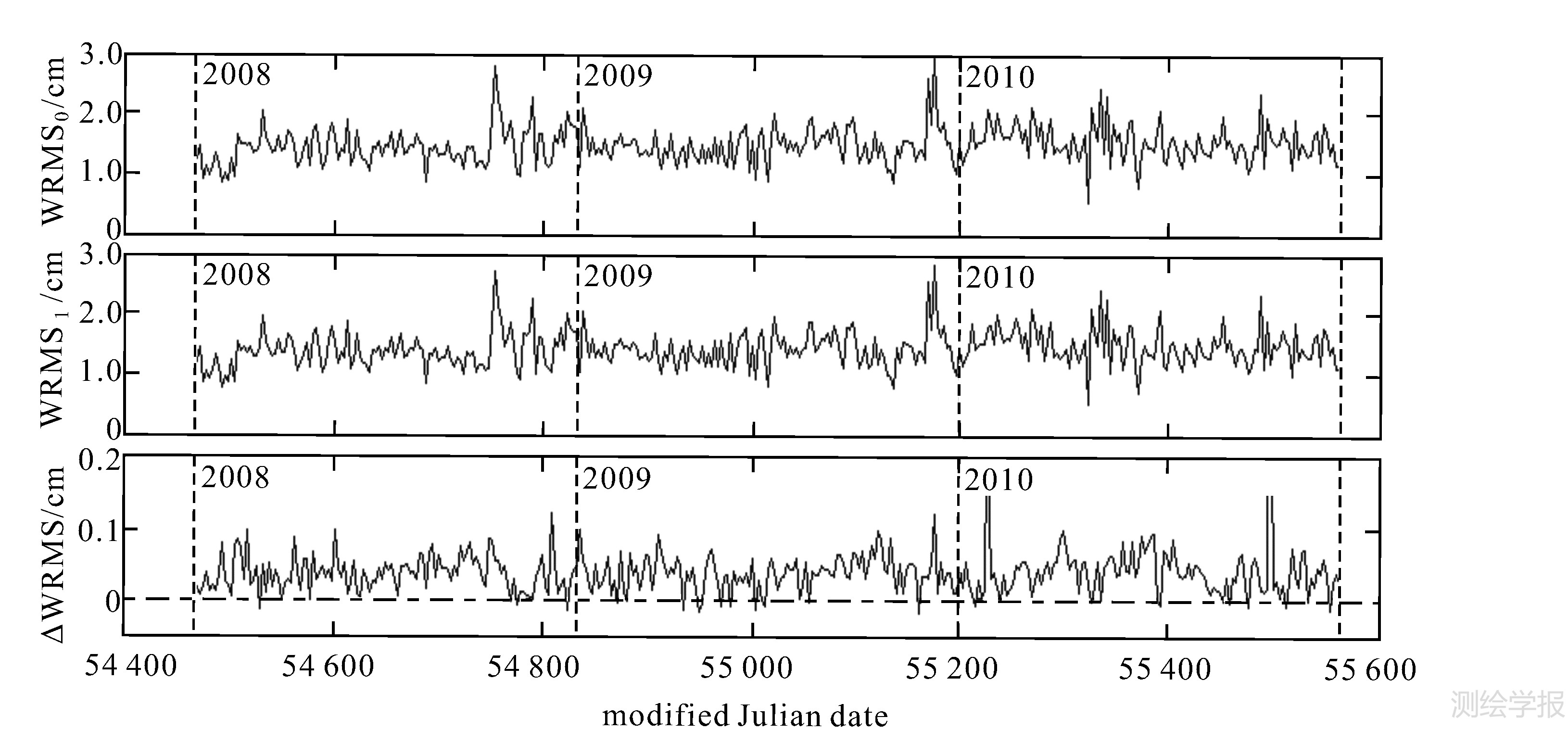
|
| 图 2 Lageos-2定轨精度及其提高量(各分图含义同图1) Fig. 2 Same as Fig.1, but for Lageos-2 |
| 卫星名称 | Lageos-1 | Lageos-2 | Etalon-1 | Etalon-2 |
| 数据时间跨度 /d | 1095 | 1095 | 1092 | 1092 |
| 弧段总数量 | 365 | 365 | 156 | 156 |
| 原弧段平均标准点数 | 637 | 588 | 170 | 156 |
| 现弧段平均标准点数 | 637 | 588 | 171 | 156 |
| 原平均定轨精度/mm | 14.27 | 14.44 | 11.88 | 11.92 |
| 现平均定轨精度/mm | 13.85 | 14.08 | 11.26 | 11.32 |
| 平均定轨精度
提高量/mm |
0.42 | 0.36 | 0.62 | 0.60 |
| 定轨精度提高弧段
百分比/(%) |
94.0 | 91.8 | 75.0 | 73.1 |
对Etalon-1从2008-01-01—2010-12-27,共156个7d弧段分别应用原质心改正和现质心改正进行定轨,结果如图 3所示。Etalon-2与之类似,结果如图 4所示。由于Etalon-1/2数据量明显少于Lageos-1/2,即使采用更宽松的收敛准则,仍有极少数弧段因观测数据太少或全球分布严重不均匀造成定轨精度过低甚至轨道发散。为有效利用观测数据,并未舍弃这些弧段,而是采取合理增加定轨弧长(至14d),或将精度较差测站的时距偏差作为待估参数进行解算,这样所有弧段定轨精度都好于3cm。对Etalon-1/2定轨结果的分析表明:① 对于Etalon-1/2,7d短弧定轨精度普遍也在1~2cm;② 采用现质心改正后,定轨精度平均提高幅度约0.6mm。提高普遍程度虽然不及Lageos-1/2,但这种提高也是系统性的,如表 3第4列和第5列所示,占到全部统计弧段约3/4。
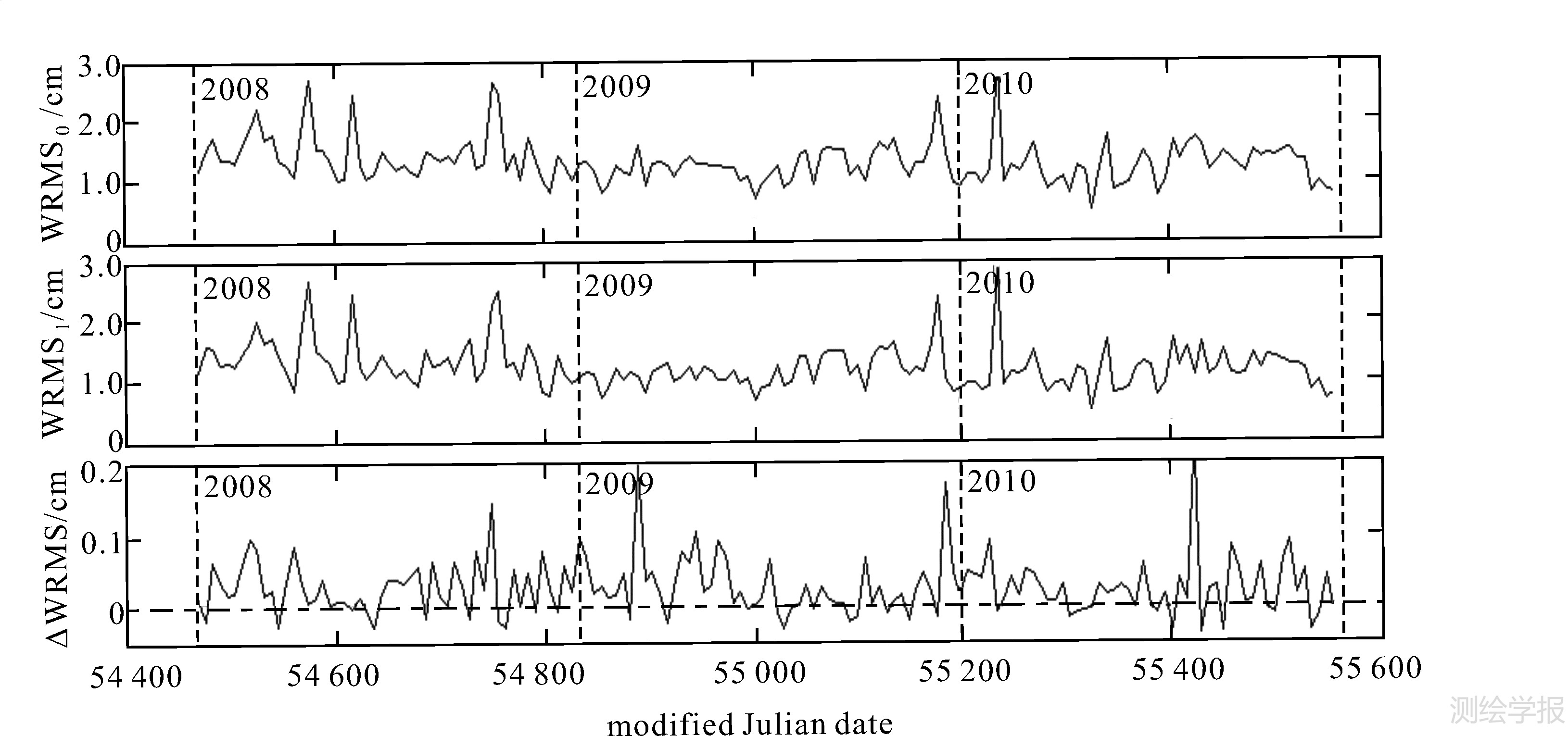
|
| 图 3 Etalon-1定轨精度及其提高量(各分图含义同图1) Fig. 3 Same as Fig.1, but for Etalon-1 |
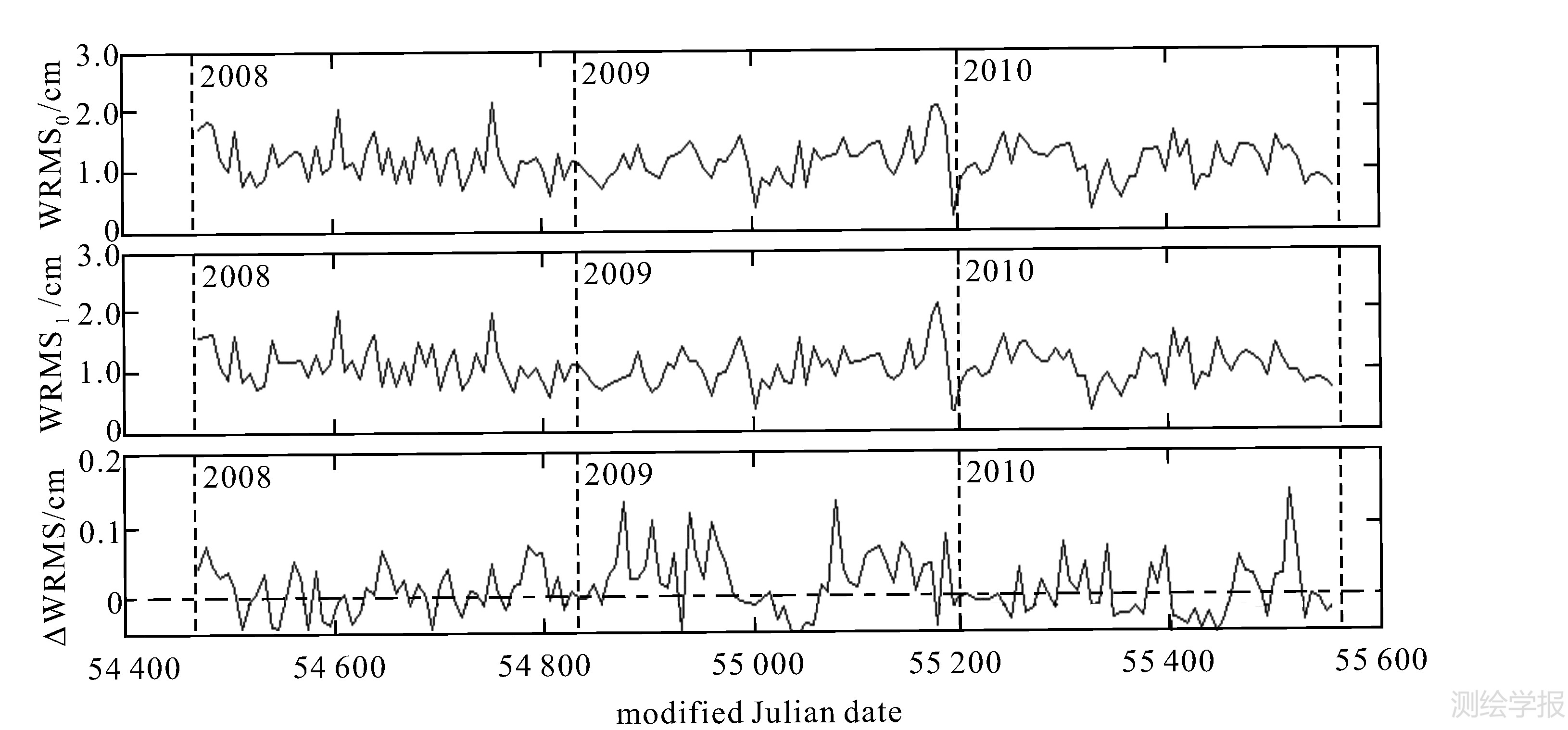
|
| 图 4 Etalon-2定轨精度及其提高量(各分图含义同图1) Fig. 4 Same as Fig.1, but for Etalon-2 |
从表 3中还可以看出,采用原质心改正和现质心改正,对最终参与定轨(即按3σ标准未被剔除)的标准点数几乎没有影响,这说明对观测数据的剔除不是造成定轨精度变化的原因。
造成Etalon-1/2相对于Lageos-1/2精度提高弧段比例偏低的可能原因,一是Etalon-1/2观测的数量和全球分布状况不如Lageos-1/2,导致精密定轨稳定性不够;二是Etalon-1/2直径(1.294m)大于Lageos-1/2(0.6m),并且Etalon-1/2的角反射器呈分片分布状态[8],而Lageos-1/2角反射器是均匀分布的[7],这可能导致Etalon-1/2的质心改正精度明显偏低。 4 总结
通过对4颗激光测地卫星实测数据的分析,研究了不同测站卫星质心不同改正对定轨精度的影响。结果表明,与全球统一质心改正相比,不同测站卫星质心不同改正可以系统性提高定轨精度。对于Lageos-1/2,超过90%弧段的定轨精度得到提高,平均提高幅度约0.4mm;对于Etalon-1/2,约75%弧段的定轨精度得到提高,平均提高幅度约0.6mm。随着各种定轨模型不断精化,在SLR定轨精度迈向毫米级的今天,这一改正将日益不可忽略,拟在未来的SLR数据常规处理中应用不同测站卫星质心不同改正。
理论和SLR实测数据分析都表明,由于卫星形状效应的影响,对不同的地面观测系统运行模式,卫星质心改正可能出现几毫米的差别。对卫星质心改正进行更为精确的处理不仅有助于提高定轨精度,而且将在未来更高精度(毫米级)ITRF的发展建立过程及SLR相关科学应用中发挥重要作用。
最后需说明的是,从卫星形状效应产生的原因来看,它不是一成不变的。如果某一测站的运行模式发生变化,这种效应对该测站数据的影响就要重新考虑,ILRS公报和报告将会给出更新的数值,SLR数据使用者也应注意这种变化,这样才能保证对SLR测量数据进行正确的质心改正,满足高精度SLR应用的需要。 致 谢:感谢ILRS提供的SLR观测数据。
| [1] | SEEBER G. Satellite Geodesy[M]. Berlin: Walter de Gruyter, 2003: 424-436. |
| [2] | GURTNER W, NOOMEN R, PEARLMAN M R. The International Laser Ranging Service: Current Status and Future Developments[J]. Advance in Space Research, 2005, 36(3): 327-332. |
| [3] | PEARLMAN M R. Workshop Summary[C]//SCHILLAK S. Proceedings of 16th International Workshop on Laser Ranging. Poznan: Polish Academy of Sciences, 2009: 4-8. |
| [4] | ALTAMIMI Z, COLLILIEUX X, METIVIER L. ITRF2008: An Improved Solution of the International Terrestrial Reference Frame[J]. Journal of Geodesy, 2011, 85(8): 457-473. |
| [5] | ZHAO Chunmei, QU Feng, CHENG Pengfei, et al. Data Quality Analysis of Argentina San Juan Laser Ranging System[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 338-341. (赵春梅, 瞿锋, 程鹏飞, 等.阿根廷圣胡安激光测距系统的SLR数据质量分析[J]. 测绘学报, 2008, 37(3): 338-341.) |
| [6] | TORRENCE M. SLR Global Performance Report Card[EB/OL].[2011-01-04]. http://ilrs.gsfc.nasa.gov/stations/site_info/global_report_cards/perf_2010q4_wLLR.html. |
| [7] | MINOTT P, ZAGWODZKI T W, VARGHESE T, et al. Prelaunch Optical Characterization of the Laser Geodynamic Satellite(LAGEOS-2)[C]//NASA Technical Paper: TP-3400. Washington: NASA, 1993: 110-145. |
| [8] | MIRONOV N, EMETZ A, ZAHAROV A, et al. ETALON-1, -2 Center of Mass Correction and Array Reflectivity[C]//Proceedings of 8th International Workshop on Laser Ranging Instrumentation. Greenbelt: NASA, 1993: 9-32. |
| [9] | EANES R, RIES J. Analysis Center Report of Center for Space Research[C]//International Laser Ranging Service 1999 Annual Report. Greenbelt: NASA, 2000: 157-163. |
| [10] | APPLEBY G M. Satellite Signatures in SLR Observations[C]//Proceedings of 8th International Workshop on Laser Ranging Instrumentation. Annapolis: NASA, 1993: 2-9. |
| [11] | NEUBERT R. An Analytical Model of Satellite Signature Effects[C]//Proceedings of 9th International Workshop on Laser Ranging Instrumentation. Canberra: Australian Government Publishing Service, 1994: 82-91. |
| [12] | FAN Jianxing, YANG Fumin, CHEN Qixiu. Theoretical Analysis and Numerical Solution of Laser Pulse Transformation for Satellite Laser Ranging[J]. Science in China: Series A, 2001, 44(7): 915-922. |
| [13] | OTSUBO T, APPLEBY G M. System-dependent Center-of-mass Correction for Spherical Geodetic Satellites[J]. Journal of Geophysical Research, 2003, 108(B4): 2201-2210. |
| [14] | APPLEBY G M, OTSUBO T, PAVLIS E C. Cannonball Spacecraft Center-of-mass Offset Modeling[C]//International Laser Ranging Service 2007-2008 Report. Greenbelt: NASA, 2009: 3-5. |
| [15] | PEARLMAN M R, DEGNAN J J, BOSWORTH J M. The International Laser Ranging Service[J]. Advances in Space Research, 2002, 30(2): 135-143. |
| [16] | FENG Chugang, ZHU Yuanlan, ZHANG Feipeng. Determination of LAGEOS Satellite's Precise Orbits and Residual Analysis[J]. Acta Astronomica Sinica, 2003, 44(1): 55-64. (冯初刚, 朱元兰, 张飞鹏.LAGEOS卫星精密定轨及残差分析[J]. 天文学报, 2003, 44(1): 55-64.) |
| [17] | FENG Chugang, TAN Detong, ZHU Yuanlan, et al. Research on Precise Determination of Orbit of Etalon Satellite[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(2): 109-116. (冯初刚, 谭德同, 朱元兰, 等.对ETALON卫星的精密定轨研究[J]. 测绘学报, 1997, 26(2):109-116.) |
| [18] | TAPLEY B D. Statistical Orbit Determination Theory[C]//Proceedings of the NATO Advanced Study Institute in Dynamical Astronomy: Recent Advances in Dynamical Astronomy. Dordrecht: Reidel, 1973: 396-425. |


