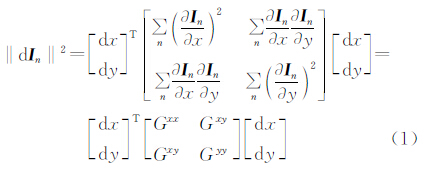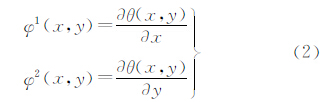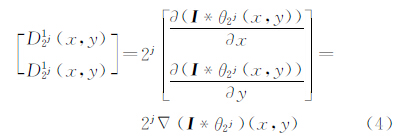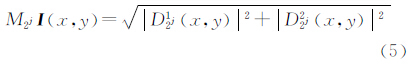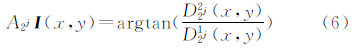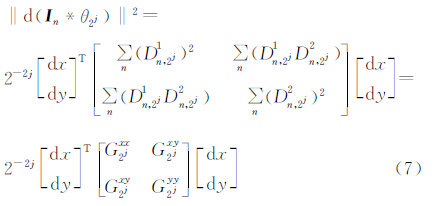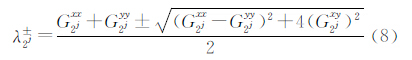2. 斯图加特大学 区域发展规划研究所,斯图加特 70569
2. Institute of Regional Development Planning, Stuttgart University, Stuttgart 70569, Germany
1 引 言
高分辨率遥感图像的边缘集中了图像的大部分信息,它的确定与提取对于整个图像的识别与理解是非常重要的[1]。目前,对高分辨率遥感图像的理解与识别已展开了大量的研究,尤其是城市道路、建筑物的提取[2, 3],但主要集中在单波段(即全色波段)图像的研究上。比起单波段图像,多光谱图像具有丰富的光谱信息,为地物的边界和地物目标的识别创造了良好的条件[4]。随着多光谱图像空间分辨率的提高,对多光谱图像处理的要求也越来越高。
自文献[5]给出了3种定义彩色图像边缘的方法以来,发展了大量的彩色图像边缘检测方法:灰度检测算子的扩展,即先对彩色图像每个波段分别进行检测,再将结果进行综合[6],或者将多维图像变换到低维空间进行检测。本质上讲,这些方法还是灰度边缘检测的方法,没有建立多光谱边缘检测的理论与方法。利用灰度算子检测边缘,图像中某一个点在3个波段上虽具有相同的梯度模,但可能有不同的方向,进行综合提取多光谱图像边缘容易造成边缘漏检和伪边缘。同时,卫星传感器的不同波段探测的是地物的不同物理化学特性,地物边缘在不同波段图像会在不同程度上存在不一致,降维处理会引起地物边界出现较大的不确定性。
遥感数据反映传感器接收到的地表能量,是平方可积的离散函数,可以利用相互正交的L2空间中的向量分析方法进行分析。根据向量场模型,多光谱遥感图像可视为一个二维、多属性的向量场,像元的多光谱数据为一个向量,则图像上地物边界的确定问题可转换为微分几何的高维曲面邻域差分问题,可以运用“第一基本形式(first fundamental form,FFF)”[7]进行求解。FFF只能用来刻画图像单个尺度的变化信息。在高分辨率遥感图像上,需要检测不同尺寸大小的多个目标,边缘信息的表征也常会存在于多个尺度,难以确定唯一尺度以适应遥感图像上不同目标的识别[8]。小波变换能够提供多分辨率分析并且具有较好的时频变化特性,能够在大尺度下抑制噪声,可靠地识别边缘,在小尺度下精确定位。
本文提出一种结合向量场模型和小波变换的高分辨率多光谱图像的多尺度边缘检测算法,并在算法过程中引入两种梯度方向量化邻域模型。首先,对多光谱图像进行二进小波变换,获取不同尺度的小波细节系数,根据FFF计算梯度幅值和梯度方向,最后根据非极大值抑制算法对梯度幅值进行细化,获取边缘点。其中,在利用梯度方向进行模极大值检测过程中,发现量化的梯度方向对提取地物边缘的完整性具有一定的影响,需要根据图像地物结构的方向选择适宜的量化邻域模型。选用Quickbird多光谱图像中多种地物类型进行试验,采用F测度[9]对试验结果进行精度评价,并与传统算子检测结果进行比较。
2 基于向量场的图像边缘检测原理 2.1 第一基本形式根据黎曼几何,对于具有n个波段的连续多值图像In,n=1,…,N,像素点对应在向量空间In中的对应矢量I=[I1(x,y) I2(x,y) … In(x,y)]。在欧氏空间内,考虑其一阶微分形式[7]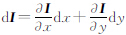 ,dI反映两个无限邻近点之间的距离,定义其作为向量图像的“第一基本形式”,即三维曲面上沿任一给定方向的弧长微元的平方的表达式为
,dI反映两个无限邻近点之间的距离,定义其作为向量图像的“第一基本形式”,即三维曲面上沿任一给定方向的弧长微元的平方的表达式为
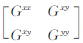 的特征向量反映了该多光谱图像的最大和最小变化方向,相应的特征值反映了其变化率的大小。
的特征向量反映了该多光谱图像的最大和最小变化方向,相应的特征值反映了其变化率的大小。
对于灰度图像,最大的特征值就是其差分的模平方,即梯度幅度的平方,相应的特征向量位于最大梯度的方向上;其他特征值皆为0。多值图像所有的特征值都不为0。当特征值λ1 λ2时,不同波段之间的梯度方向在同一个方向上(相同或者相反);当λ1≌λ2时,不同波段之间的梯度方向无优先顺序。但在任何情况下,较大的特征值λ1都能够提供充足的多值图像的边缘信息[10]。以下均以In代表为多光谱图像,I为单波段图像。
λ2时,不同波段之间的梯度方向在同一个方向上(相同或者相反);当λ1≌λ2时,不同波段之间的梯度方向无优先顺序。但在任何情况下,较大的特征值λ1都能够提供充足的多值图像的边缘信息[10]。以下均以In代表为多光谱图像,I为单波段图像。
设θ(x,y)为二维可微平滑函数,对x和y的积分都是1,且在无穷远处收敛到0。定义
为小波函数。在L2(R2)中,二维图像I(x,y)在尺度为2j上的二进小波变换为 式中,*为卷积运算;L2j、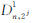 和
和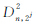 分别是I的j级低通分量和两个高通分量。可以证明
小波变换后的两个细节分量同梯度矢量∇(I*θ2j)(x,y)的两个分量成正比。在尺度2j上,梯度矢量的模正比于小波变换的模
梯度矢量与水平方向的夹角(相角)为
分别是I的j级低通分量和两个高通分量。可以证明
小波变换后的两个细节分量同梯度矢量∇(I*θ2j)(x,y)的两个分量成正比。在尺度2j上,梯度矢量的模正比于小波变换的模
梯度矢量与水平方向的夹角(相角)为
在尺度2j,平滑后图像中尖锐变化的地方使梯度模函数沿幅角有极大值点,该极大值点即为图像的边缘。对于二维图像上一点(x,y),可以根据公式(6)给出的方向对小波变换的模进行局部模极大值检索获取图像的边缘点。
对于多值图像In,n=1,…,N,根据FFF,(In*θ2j)(x,y)微分形式的平方模为
式中,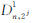 和
和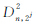 为第n波段图像在第j级尺度上的细节分量。
为第n波段图像在第j级尺度上的细节分量。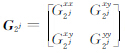 的特征根可用下式简化计算
对应的特征向量为
的特征根可用下式简化计算
对应的特征向量为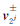 =(cosθ±,sinθ±),其中,
=(cosθ±,sinθ±),其中,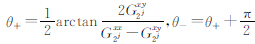 。
。
表达式(7)称为第j尺度基本形式,反映了平滑后的图像在2j尺度上的边缘信息。对于多值图像中的给定像素点,矩阵G2j的特征向量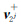 和
和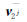 代表了其最大和最小变化方向,特征值
代表了其最大和最小变化方向,特征值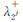 和
和 则表示其相应的变化幅值。特征值和特征向量在图像平面上构成椭圆,椭圆的长轴表示2j尺度的梯度主方向,短轴代表梯度主方向周围的差异值。
则表示其相应的变化幅值。特征值和特征向量在图像平面上构成椭圆,椭圆的长轴表示2j尺度的梯度主方向,短轴代表梯度主方向周围的差异值。
当N=1时,即灰度图像,矩阵G2j的秩为1,最小特征值 =0,即椭圆短轴为0,最大特征值
=0,即椭圆短轴为0,最大特征值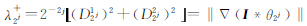 为平滑后图像在第j尺度的梯度幅值,指向图像j尺度的梯度最大方向;当N>1时,即多值图像,
为平滑后图像在第j尺度的梯度幅值,指向图像j尺度的梯度最大方向;当N>1时,即多值图像, 不一定为0。边缘信息包含在矩阵Gj2两个特征值和对应的特征向量中。图像In在第j尺度上的4个细节图像表示为
不一定为0。边缘信息包含在矩阵Gj2两个特征值和对应的特征向量中。图像In在第j尺度上的4个细节图像表示为
由式(7)得到的多值图像不同尺度下的局部变化量远大于单个图像分量给定像素点的变化量,且其特征向量没有唯一确定。文献[10]用图像小波变换的平均值来确定特征向量及其方向。 2.3 基于向量场边缘检测和梯度方向量化
在有噪音环境下进行图像的边缘特征识别,需要在噪音抑制和边缘准确定位之间进行均衡,B样条小波边界检测算子在边界检测综合性能指标上是较佳的,文献[11]从时频局部化的角度对不同次数的B样条函数作分析,认为三次B样条在作为平滑函数边缘提取中是渐进最优的。
故选用三次B样条函数作为平滑函数,其一阶导数作为小波函数。根据公式(3),获取多光谱图像In经过三次B样条函数平滑后的梯度,根据式(6)和式(7)计算在2j尺度上,多光谱图像In的梯度幅值和梯度方向。
根据文献[8],本文中,在第j尺度上,对图像的给定像素点(x,y),取多光谱图像梯度向量的模为
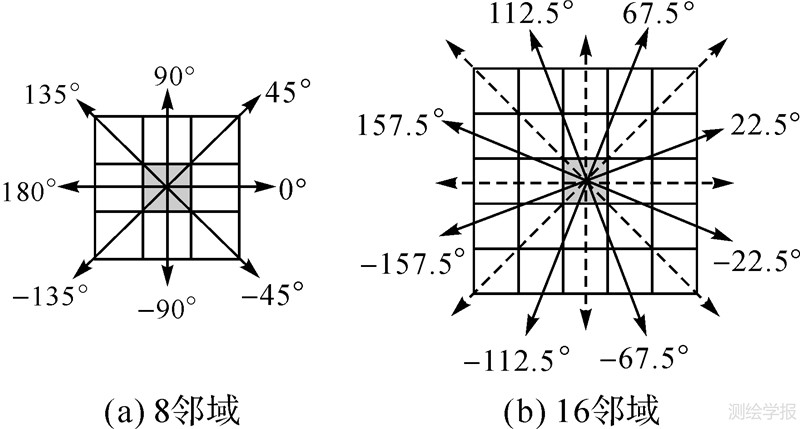
梯度的方向即相角取为θ+,模Grad沿θ+的局部极大值点,即图像的边缘点。不同波段图像梯度方向存在一定的差异,当不同波段图像梯度具有相同幅值但方向相反时,直接进行梯度矢量求和结果的梯度值为0,在进行多光谱图像边缘特征重构时必须考虑量化梯度方向问题。在遥感图像上,地物类型复杂,可只考虑每个像素点的8邻域方向,即8个区间,当θ+在某一区间内,可量化为由该区间内中间梯度方向表示的特征矢量,相反的梯度方向具有相同的影响,8邻域梯度方向可量化为0°、45°、90°和135° 4个方向,量化后梯度方向指向梯度的模极大值的方向。图 1(a)为根据8邻域方向进行量化,实线指向量化后的梯度方向:①若θ+∈[-22.5°,22.5°)∪[157.5°,180°)∪[-180°,-157.5°),θ=0°或180°(此处取0°);②若θ+∈[22.5°,67.5°)∪[-157.5°,-112.5°),θ=45°;③若θ+∈[67.5°,112.5°)∪[-112.5°,-67.5°),θ=90°;④若θ+∈[112.5°,157.5°)∪[-67.5°,-22.5°),θ=135°。
|
| 图 1 梯度方向量化 Fig. 1 Gradient orientation quantification |
在试验中发现,针对高分辨率图像中具有明显方向性且该方向与8邻域方向有所偏移的地物,仅考虑8邻域是不够的,在根据梯度方向检测边缘点的过程中会丢失部分边缘点,需要分析地物纹理方向与量化梯度方向之间的关系,并对量化区间进行适当的调整,可以进一步细化为16邻域方向。图 1(b)为按16邻域进行梯度量化的方向,为显示需要,用实线表示细化补充的检测方向,虚线表示原始的8邻域方向。
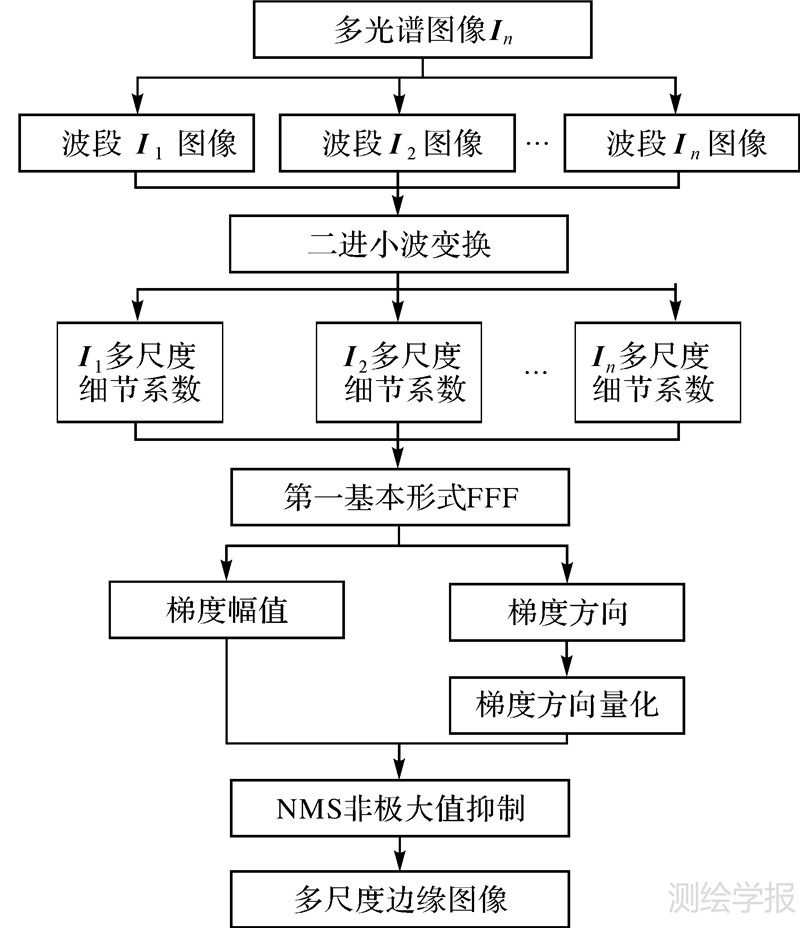
3 试验及分析 3.1 基于向量场多尺度边缘检测试验试验数据为南京幅QuickBird(成像时间2004-11-21)图像,同时具有全色图像和多光谱图像,空间分辨率分别为0.61 m和2.44 m。利用PANSHARP方法,将多光谱图像与全色图像进行融合,获取与全色图像相同的空间分辨率,又保持多光谱和边缘特性,图像质量得到显著增强。试验在融合后多光谱图像上裁取了厂房、农田等典型地物图像(512像素×512像素)以及具有较多地物的图像(2048像素×2048像素)。限于篇幅,所有图像都缩小显示,采用假彩色合成。算法流程如图 2所示。
|
| 图 2 算法流程图 Fig. 2 Flowchart of the proposed method |
小波变换时的边界条件采用镜面投影处理,每个尺度的小波变换都提供了一定的边缘信息,因此在图像边界,边缘可能产生失真,而且随着尺度的增大,失真越严重。所以,为保持边缘的准确性,一般取尺度数不宜超过4,试验取次数为3。从试验中也可以看出:前3个尺度之间的边缘像素的位移几乎可以忽略。
图 3显示QuickBird多光谱图像上厂房多尺度边缘梯度特征。在j=1尺度,厂房屋顶的细小结构检测出来,随着尺度的增大,厂房周围的植被信息被模糊,边缘特征突出了厂房的整体结构特征,表征整个图像的整体内容;图 4是对农田的检测结果。图 4(b)为最精细的边缘信息,包括农田内部的精细几何细节,但是需要提取的是规则的田埂以及因农田内部种植的不同作物而具有的不规则的边界。如图中白色框,随着尺度增加,农田内部不规则边缘信息也被检测,更加符合对农田信息提取的需求;图 5(a)提供了更加丰富的地物信息,在j=1尺度,精细的地物的边缘信息得到较为突出地检出。该类地物边缘大致占图像3~30像素,较之整幅图像大小(2048像素×2048像素)该类地物属于最为精细纹理信息,且具有较强辐射特征。在该尺度形成的边缘特征较为连续完整,能够精确地确定边缘子像素位置;在j=2和3的检测结果中,农田及右上方的河道的结构信息被检测出,显示了图像的结构信息。

|
| 图 3 厂房图像多尺度边缘特征 Fig. 3 Multiscale edge detection results of factory at three scales |

|
| 图 4 QuickBird多光谱农田图像多尺度边缘特征 Fig. 4 Multiscale edge detection results at three scales and comparison with Canny,Sobel gradient |

|
| 图 5 QuickBird多光谱图像多尺度边缘特征 Fig. 5 Multiscale edge detection results at three scales and comparison with Canny,Sobel gradient |
根据Lam等提出的4种空间尺度类型,即制图尺度或地图尺度、地理尺度、分辨率和运行尺度[13]。试验中厂房屋顶精细的结构为3~30像素,稍大于图像分辨率,j=1尺度为较适宜尺度;在检测过程中,关注的是农田的规则田埂信息以及农田内部的不同类型作物间不规则的边缘信息,普遍地,农田的尺寸远大于图像分辨率,较为适合在较大尺度上检测。
对比经典算子的检测结果,考察图 4和图 5,Canny算子抑制噪声效果较好,Sobel获取的边缘信息较为突出,但仅能提供图像单一尺度的边缘信息,在该尺度上,高分辨率图像地物目标内部精细的几何信息也都得到检出,但以噪声的形式存在。同时,综合每个波段图像的检测结果作为多光谱图像边缘,提取的梯度幅值较宽,在后续边缘细化过程中会有一定程度偏移。利用小波变换进行滤噪,小尺度下对边缘点精确定位,大尺度下滤除噪声。
3.3 梯度方向量化及非极大值检测试验考虑梯度方向量化的邻域模型,量化梯度方向,并进行模极大值检测。高分辨率图像地物目标内部具有非常精细的几何特征,获取的模极大值图像存在较多噪点,采用偏微分方程(partial differential equations,PDE)[14]滤噪,能够很好地保持边缘,并有效去除图像的高斯和椒盐噪声。
图 6中厂房结构的方向集中在45°和135°,即8邻域方向。从试验结果来看,在j=1下,8邻域将精细地物边缘点检出,连续并且完整;随着尺度的增加,检出的连续边缘点对结构性特征的表现更为突出,而16邻域边缘点则不连续;图 7中农田边缘方向更多集中在16邻域方向,与8邻域方向有所差异。从检测结果(图中红色框所示)中亦可看出,利用16邻域对农田边缘点检测对提取具有完整连续的农田边缘信息更有优势。限于篇幅,文中未列出所有尺度下的检测结果。

|
| 图 6 厂房细化边缘点结果对比(按两种邻域模型) Fig. 6 Edge point location of factory image (based on eight and sixteen neighborhood) |

|
| 图 7 农田细化边缘点结果对比(按两种邻域模型) Fig. 7 Edge point location of paddy image (based on eight and sixteen neighborhood) |
对于具有较多地物的遥感图像,如图 5。根据3.2节分析可知,j=1和j=2尺度主要提取道路信息,j=3尺度突出农田等结构信息。道路及建筑物信息方向集中于8邻域,而农田为16邻域,可在前两个尺度采用8邻域,j=3采用16邻域。试验亦获得了较好结果,限于篇幅,未列出结果图像。
通常情况下,利用8邻域进行梯度方向量化可以检测出足够的边缘信息。在对高分辨率图像典型地物进行特征检测时,可以考察图像纹理方向,选择合适的量化邻域模型,以能够获取更为符合实际的连续边缘点。试验表明,选用16邻域对计算效率影响不大。
3.4 精度评价选用厂房图像作详细的对比分析和精度评价。考察图 8,本文算法将多光谱图像作为向量模型,充分利用多个波段信息,精确地确定边缘点位置,不会产生伪边缘,比零交叉更优越;获取的梯度特征大多为单像素宽,采用经典算子综合4个波段信息提取的梯度幅值较宽,梯度方向不稳定,Zerocrossing结果中出现了部分伪边缘。

|
| 图 8 不同厂房边缘检测结果对比 Fig. 8 Edge detection result at j=1 scale of factory image compared with Canny,Sobel and Zerocrossing operator |
对图 8中梯度幅值进行模极大值检测获得单像素宽边缘,引入F测度(F-measure)对边缘准确度进行监督评价。F测度包括准确度P和召回度R两部分。精确度P指在一定误差距离范围内,边界像素在参考图中对应的点数目与分割结果点数目的比值;召回度R指在一定误差距离范围内,参考图中边界像素在分割结果中对应的边缘点数目与参考图中所有边缘点的数目之比。根据文献[9],从过分割到欠分割,P逐渐升高,R逐渐下降,为均衡这种变化趋势,定义F测度为F=PR/(αP+(1-α)R),用于表征边缘结果精度,其中α为权重,设定为0.5。本文中的误差距离范围定为2个像素,结果如下。
| P | R | F | ||
| 本文 算法 |
j=1尺度 | 75.03% | 86.27% | 80.27% |
| j=2尺度 | 69.96% | 87.17% | 73.22% | |
| j=3尺度 | 69.63% | 56.81% | 62.57% | |
| Canny | 52.11% | 89.11% | 65.76% | |
| Sobel | 84.99% | 63.57% | 72.73% | |
| Zerocrossing | 57.66% | 83.20% | 68.11% | |
根据参考图像,在j=1到3的检测结果中,F测度下降,P稳定,表明即使经过小波变换,边缘点仍然能够精确定位,j=3结果R较低,是因为该尺度检测的主要是图像的结构信息,精细的边缘信息被忽略。Canny和Zerocrossing的P较低,存在边缘漏检;R较高,是因为综合4个波段的值梯度幅值较宽,边缘点较多,有一定伪边缘;Sobel为经典的灰度检测算子,P值较高,获得的边缘点定位精确,但有较多边缘漏检。总体上,本文算法能够获得较高的检测效果。
4 结 论对同一空间分辨率的影像进行不同尺度的边缘信息检测,可以形成不同尺度的影像对象层次网络体系,不同地物由其最适宜的尺度来进行描述,并在该尺度上进行地物边缘信息的检测[15]。在利用梯度方向进行边缘点检测的过程中,考察图像中地物方向与梯度方向量化邻域模型的关系,试验表明,针对不同地物类型选择不同的邻域模型进行边缘点提取,能够更加有效提取完整连续的边缘点,并获得较高的精度评价。
在后续研究中,将进行边缘综合和边缘连接试验,实现面向对象的图像分割。同时,可以进一步考虑地物大小与图像分辨率之间的关系在不同检测尺度上的表征,定量描述高分辨率图像上地物的适宜检测尺度,找到不同尺寸类型的地物在高分辨率图像分析中的最适宜尺度。
| [1] | XIAO Pengfeng, FENG Xuezhi, ZHAO Shuhe,et al. Segmentation of High-resolution Remotely Sensed Imagery Based on Phase Congruency[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 304-311.(肖鹏峰,冯学智,赵书河,等.基于相位一致的高分辨率遥感图像分割方法[J].测绘学报, 2007, 36(2): 304-311.) |
| [2] | LI Xiaofeng, ZHANG Shuqing, HAN Fuwei, et al. Road Extraction from High-resolution Remote Sensing Images Based on Multiple Information Fusion[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 178-184. (李晓峰,张树清,韩富伟,等.基于多重信息融合的高分辨率遥感影像道路信息提取[J].测绘学报, 2008, 37(2): 178-184.) |
| [3] | TAN Qulin. Urban Building Extraction from VHR Multispectral Images Using Object Based Classification [J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 618-623. (谭衢霖.高分辨率多光谱影像城区建筑物提取研究[J].测绘学报, 2010, 39(6): 618-623.) |
| [4] | SHU Ning. Strengthen the Researching of the Theories and Methods of the Multispectral Images Comprehension [J]. Remote Sensing for Land and Resources, 1999, 3(41): 28-30. (舒宁.应加强多光谱图像理解[J].国土资源遥感, 1999, 3(41): 28-30.) |
| [5] | NEVATIA. A Color Edge Detector and Its Use in Scene Segmentation [J]. IEEE Transactions on Systems, Man and Cybernetics, 1977, 7(11): 820-826. |
| [6] | KUNG S Y, HU Y H. A Highly Concurrent Algorithm and Pipelined Architecture for Solving Toeplitz Systems [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1983, 31(1): 66-76. |
| [7] | CUMANI A. Edge Detection in Multispectral Images[J]. Graphical Models and Image Processing, 1991, 53(1): 40-51. |
| [8] | ZHAO Xian, LI Deren. Constructing Two Dimension Symmetric Wavelets for Extracting Edge Features of Image at Multiscales [J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 313-319. (赵西安,李德仁.二维对称小波与多尺度影像边缘特征提取[J].测绘学报, 2003, 32(4): 313-319.) |
| [9] | MARTIN D R, FOWLKES C, MALIK J. Learning to Detect Natural Image Boundaries Using Local Brightness, Color and Texture Cues [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(5): 530-549. |
| [10] | SCHEUNDERS P. A Multivalued Image Wavelet Representation Based on Multiscale Fundamental Forms[J]. IEEE Transactions on Image Processing, 2002, 10(5): 1204-1211. |
| [11] | WANG Yuping, CAI Yuanlong. Multi-scale Spline Wavelet Edge Detection Operator [J]. Science in China (Series A), 1995, 25(4): 426-437. (王玉平,蔡元龙.多尺度样条小波边缘检测算子[J].中国科学: A辑, 1995, 25(4): 426-437.) |
| [12] | SAPIRO G, RINGACH D L. Anisotropic Diffusion of Multivalued Images with Applications to Color Filtering [J]. IEEE Transactions on Image Processing, 1996, 5(11): 1582-1586. |
| [13] | MING Dongping, WANG Qun, YANG Jianyu. Spatial Scale of Remote Sensing Image and Selection of Optimal Spatial Resolution[J]. Journal of Remote Sensing, 2008, 12(4): 529-537. (明冬萍,王群,杨建宇.遥感影像空间尺度特性与最佳空间分辨率选择[J].遥感学报, 2008, 12(4): 529-537.) |
| [14] | PERONA P, MALIK J. Scale-space and Edge Detection Using Anisotropic Diffusion [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639. |
| [15] | HUANG Huiping, WU Bingfang. Analysis to the Relationship of Feature Size, Objects Scales, Image Resolution[J].Remote Sensing Technology and Application, 2006,21(3):243-248.(黄慧萍,吴炳方.地物大小、对象尺度、影像分辨率的关系分析[J].遥感技术与应用,2006,21(3):243-248.) |