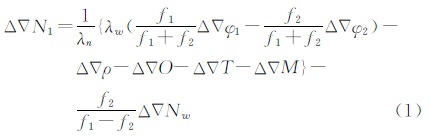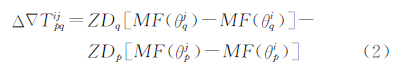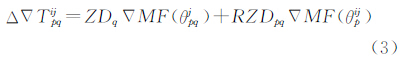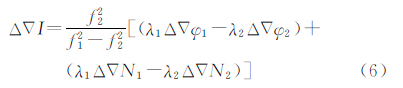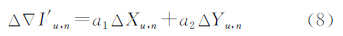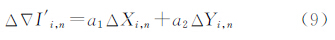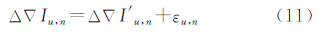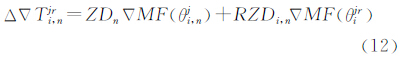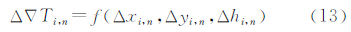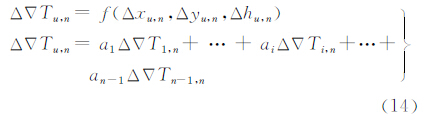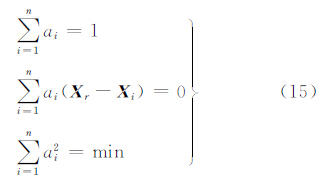2. 东南大学 仪器科学与工程学院,江苏 南京 210096
2. Department of Instrument Science and Engineering, Southeast University, Nanjing 210096, China
1 引 言
随着网络技术的飞速发展,以虚拟参考站技术(VRS)[1, 2]为代表的网络RTK技术有效地弥补了常规RTK的不足,成为GNSS厘米级高精度实时定位的一种重要手段。与常规RTK相比,网络RTK技术具有精度和可靠性高、服务范围广、精度分布均匀等优点[3, 4]。随着互联网与移动通信技术的普及,作为最具代表性的网络RTK技术——VRS技术,其性能越来越稳定,应用范围越来越广泛[5, 6, 7]。常规网络RTK技术一般采用三角形结构进行单基线模式模糊度网解[8, 9, 10]和误差建模[11, 12]。这种三角形网络结构也有一些不足之处,特别是相对于作为将来主要发展趋势的大规模、长基线网络RTK系统,该方式没有充分利用多参考站冗余观测信息,降低了系统模糊度解算速度以及改正数的可靠性,从而严重影响流动站定位速度及可靠性。为了确保大规模网络RTK定位的精度与可靠性,笔者提出了构建星型结构的VRS网络来取代传统VRS三角形网络结构,同时针对星型结构提出了相应的VRS关键算法,并进行了试验分析与比较。
2 星型拓扑结构VRS网络构建目前,网络RTK系统都是在连续运行参考站系统(CORS)基础上建立起来的。CORS基准站的分布情况将直接影响到基线模糊度解算效率和精确误差建模。在GPS差分定位中,影响定位精度的误差主要是距离相关误差,因此基准站间距离和网络分布情况均会影响误差建模的精确性[13],为此构建最优的基准站网络极其关键。由于传统VRS技术是以三角形为基本解算单元[13, 14],因此不规则三角形网络方法常常用于CORS基准站网络的构建,其中以Delaunay三角网最佳[13, 14]。
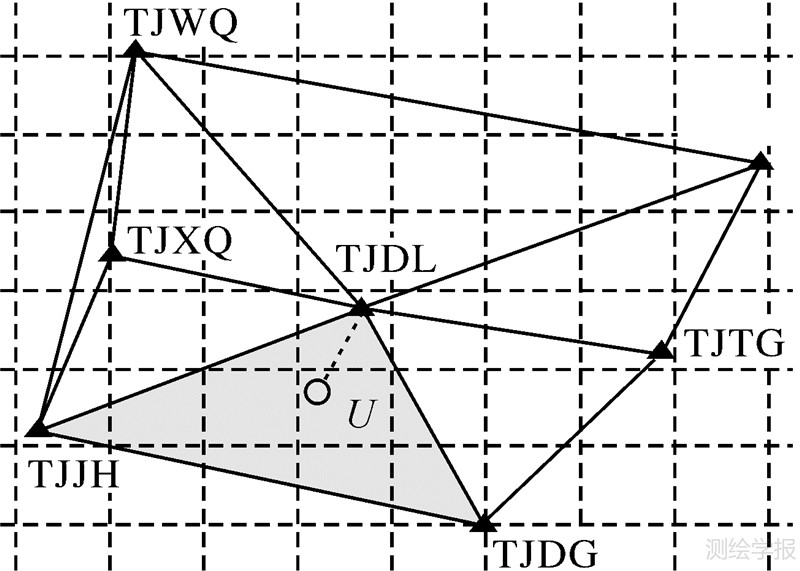
传统VRS技术,以用户所在三角形为基本解算单元建立网络改正模型,它仅选择用流动站所在的三角形区域的3个参考站及基线数据,建立覆盖三角形区域的改正计算模型。如图 1所示,图中阴影部分区域就是其中的基本解算单元。
|
| 图 1 传统VRS基本解算单元 Fig. 1 Basic solving unit of traditional VRS |
这种解算单元能保证改正区域与流动站最大程度的符合,只要该三角形解算单元网络初始化正常,就能保证较优的网络改正精度和可靠性,同时也不受其他单元初始化错误的影响。但在实践过程中笔者发现这种三角形网络结构也有一些不足之处,主要表现在:①它采用的是单基线解算模式,没有充分利用多参考站多余观测信息,导致对于长基线和低高度角卫星的模糊度固定时间较长,不利于大规模基准站网络的初始化;②独立基线信息较少(2条基线),因此限制了内插计算时可供选择的数学模型(模型参数≤2)的精确性[15],因而在一定程度上影响了改正数的精度,特别是对于高程差异较大区域的定位精度会有所降低;③对于基本解算单元以外的区域,其改正精度随距离的增加大幅下降。
本文针对传统VRS技术的基本解算单元的不足,在Delaunay三角网的基础上,提出一种星型结构的VRS网络基本解算单元。如图 2所示,为一个星型结构的基本解算单元。

|
| 图 2 星型基本解算单元 Fig. 2 Basic solving unit of star |
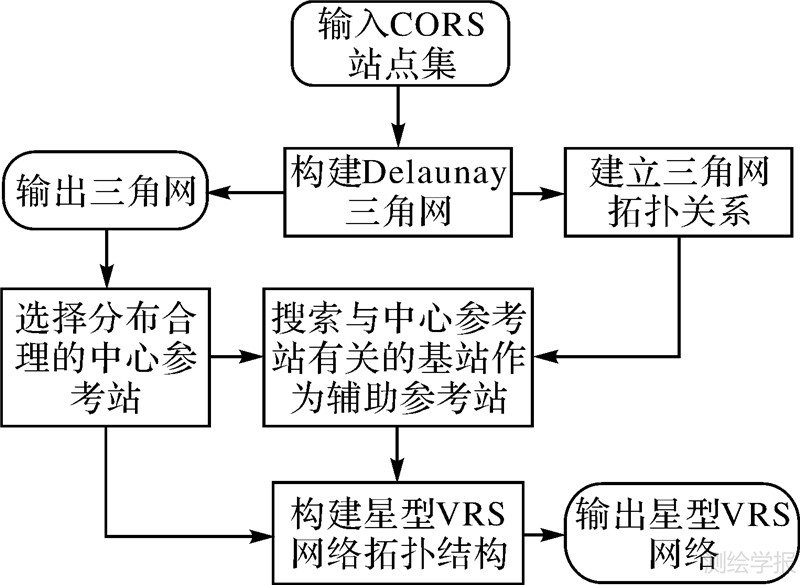
星型VRS网的建立方法是先将整个CORS网络按Delaunay三角网构网原则建立不规则三角网,然后以参考站关联的基线数以及参考站位置作为选取原则,选择其中n个参考站作为中心参考站,将与任一中心参考站形成Delaunay三角网的其余参考站作为辅助参考站,形成一个星型结构基本解算单元,从而可以将整网分成n个子网,而这些子网以星型拓扑结构构建,以中心参考站命名,具体流程图如图 3所示。
|
| 图 3 星型VRS网络结构生成流程 Fig. 3 Flow chart for the growth of star structure VRS network |
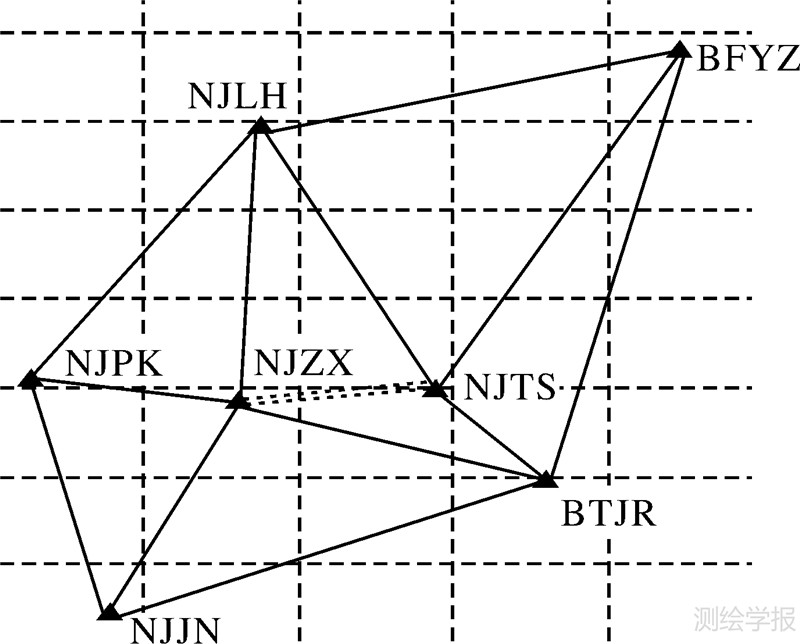
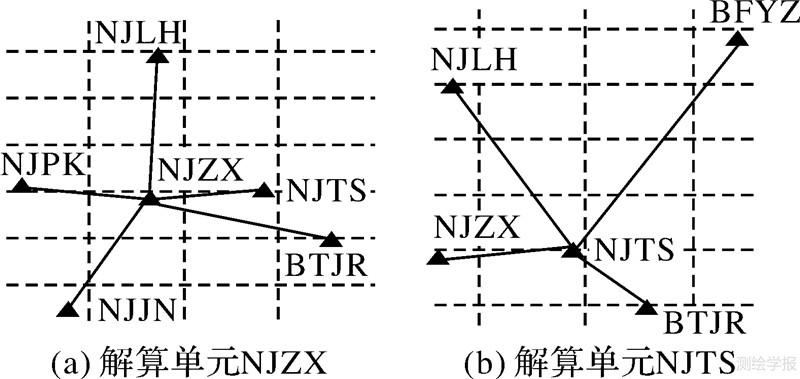
如图 4所示,选择江苏CORS的7个参考站先建立Delaunay三角网,然后选择其中的参考站NJZX站和NJTS站作为中心参考站,即可形成两个星型拓扑结构的基本解算单元,即解算单元NJZX和解算单元NJTS,如图 5所示。
|
| 图 4 JSCORS站分布图 Fig. 4 Distribution of JSCORS stations |
|
| 图 5 JSCORS星型基本解算单元 Fig. 5 Basic solving unit of star of JSCORS |
采用上述星型拓扑结构作为基本解算单元,它既继承了传统VRS三角形解算单元改正相关性强、共视卫星多的优点,又能充分利用多基站多余观测信息,提高模糊解算效率,使得内插模型灵活多样,保证了内插模型具有较好的数据冗余,提高了误差改正的精度和可靠性,同时这种星型基本解算单元有唯一的参考卫星,解算基线独立。
3 星型VRS网络模糊度解算策略对于大规模参考站网络(CORS)而言,网络模糊度解算主要是指参考站间的基线模糊度解算。无论是建立误差模型,还是计算高精度的综合误差,参考站间基线模糊度解算[8, 9, 10]是重要的前提条件。
对于传统VRS三角形解算单元来说,一般采用单基线解算模式,但这种单基线解算模式有其一定的不足。由于在三角形解算单元中,相邻的两条基线估计模糊度时存在共同的参数。该参数的估值误差对于低高度角以及长基线模糊度解算来说影响很大,大大影响了基线模糊度的解算速度,严重影响网络RTK系统的初始化。
本文提出的星型基本解算单元较传统VRS三角形解算单元具有更多的多余观测值。采用多基线解算模式,充分考虑多基线的共有参数,加快L1模糊度解算速度,特别是加快了长基线以及低高度角卫星模糊度解算速度,以利于大规模网络RTK系统的初始化。
采用两步法[10]解算策略:①由于宽巷双差模糊度能在较短时间内固定且不同卫星间相关性较小,因此直接采用单基线模式,利用宽巷组合的长波特性快速固定宽巷模糊度,本文不再详述;②本文重点介绍采用多基线模式,利用无电离层组合、宽巷模糊度与L1、L2模糊度之间的关系解算出L1、L2双差模糊度Δ∇N1、Δ∇N2。
对于星型解算单元中每一条基线在固定宽巷模糊度之后,都可采用无电离层组合分离出L1双差模糊度,其计算公式为
式中,Δ∇(·)为双差算子;λn为窄巷波长;φ、ρ、O、T、M、Nw、N1为相位观测值、卫地距、轨道误差、对流层延迟、多路径效应、宽巷模糊度、L1模糊度;f1、f2为L1、L2载波的频率。由式(1)可见,采用无电离层组合可以有效地消除电离层的影响。其中轨道误差O、多路径效应M可以忽略不计,因此影响Δ∇N1精度的主要为对流层延迟,双差对流层延迟Δ∇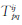 可表示为
可表示为
由于在星型解算单元中共有中心参考站的信息,故可对式(2)进行如下处理,即分离出中心参考站q的待估计参数天顶对流层延迟ZDq,如式(3)所示。
式中,RZDpq为相对天顶对流层延迟。故任意第k条基线多卫星模糊度解算模型如下
式中,r为参考卫星;s为非参考卫星;m为中心参考站;k为辅助参考站。在此基础上,采用以下策略:首先选择星型基本解算单元中基线最短的基线进行模糊度解算,构建卡尔曼滤波器[10],即可快速估计出中心参考站m的天顶对流层延迟ZDm、m与k两站相对天顶对流层延迟RZDmk以及模糊度浮点解。
由于ZDm变化非常缓慢,可把它看做随机游走过程,故设定ZDm与RZDmk的状态转移噪声方差为1 cm2/h、2 cm2/h,其初值由Hopfield模型获得;模糊度的状态转移噪声为零,其状态噪声方差也为零。
式中,Xk为tk时刻的状态向量;Xk=[ZDm RZDmk Δ∇N1…]T;Lk为观测向量,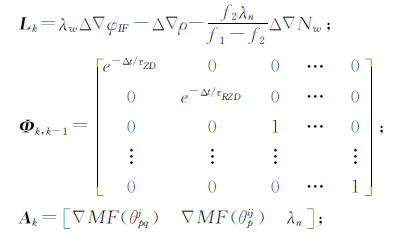
由于星型基本解算单元具有同一中心参考站m,所以可以将已估计出的天顶对流层延迟ZDm实时应用于其余基线的解算,加快模糊度浮点解解算效率,构造新的卡尔曼滤波器。此时只估计相对天顶对流层延迟RZDmk和模糊度浮点解,相关的状态噪声方差与观测值随机模型与第一个滤波器一致,与最后采用LAMBDA算法加快模糊度固定速度。
4 星型VRS网络改正数计算模型在VRS网络模糊度固定之后,则需要进行VRS网络误差改正数的计算建模[16, 17]。目前VRS的误差改正数计算模型大多采用常规内插模型,就是将所有误差综合起来进行综合误差的内插或拟合计算。但是由于多种误差之间的变化规律及相关特性存在差异,使用单一修正模型计算VRS改正数的方法在精度和可靠性上均存在不足。为此,必须对VRS误差分离进行分类建模,以利于VRS误差改正数的精化。
4.1 电离层改正数星型内插模型(SIM)由于电离层延迟误差的色散性,在固定模糊度之后,采用双频相位观测值可以计算参考站网络各基线上的电离层延迟,忽略观测噪声和高阶电离层延迟误差的影响,就可以得到基线上的电离层双差改正数,如下式
式中,Δ∇I为电离层双差改正数。由于线性内插法LIM可以很好地逼近电离层平静时段电离层延迟在参考站网络区域范围内的空间分布相关特征,且具有较强的适用性,尤其在中纬度地区,其改正数精度可达2~4 cm[15]。故本文首先利用LIM模型来计算电离层双差改正数,由此可建立基于星型解算单元的LIM模型,如式(7)所示。
式中
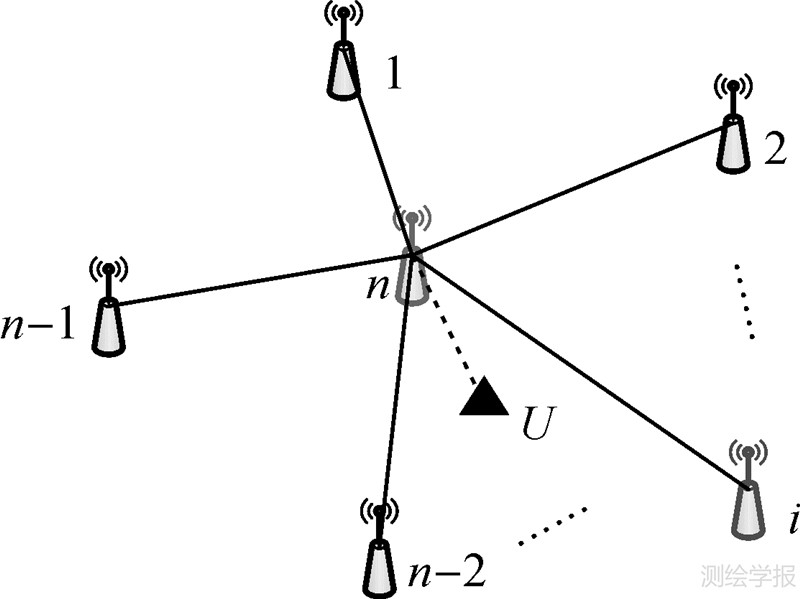
|
| 图 6 星型解算单元站点分布图 Fig. 6 Distribution of stations in solving unit of star |
则对于用户u,根据LIM特性以及式(7)可得到电离层双差改正数的空间相关线性项Δ∇I′u,n,即
在此基础上,依次以i=(1,…,n-1)作为监测站,其余参考站作为辅助站,由式(8)内插监测站i,可得到
而由式(5)可得到基线i,n的电离层改正数Δ∇Ii,n,故存在残差项εi,n,如式(10)所示。 故可建立星型解算单元所有εi,n的拟合模型εi,n=f(ΔXi,n,ΔYi,n,Δ∇Ii,n),从而可得到用户u的内插残差项εu,n,则用户其电离层改正数为 4.2 对流层改正数星型内插模型(SHM)由于对流层延迟误差受高程因子影响显著,使其在水平方向和高程方向空间相关特性存在明显差别,因此参考站与流动站间的高程差异会引起对流层误差改正数中存在系统偏差的影响,使对流层改正精度降低,故对流层改正数内插建模需要考虑高程偏差。本文提出构建三维内插模型,以建立对流层改正数星型网络内插模型。
针对图 6的星型解算单元,利用式(3)和式(4)可得到任意基线i、n的对流层双差改正数,即
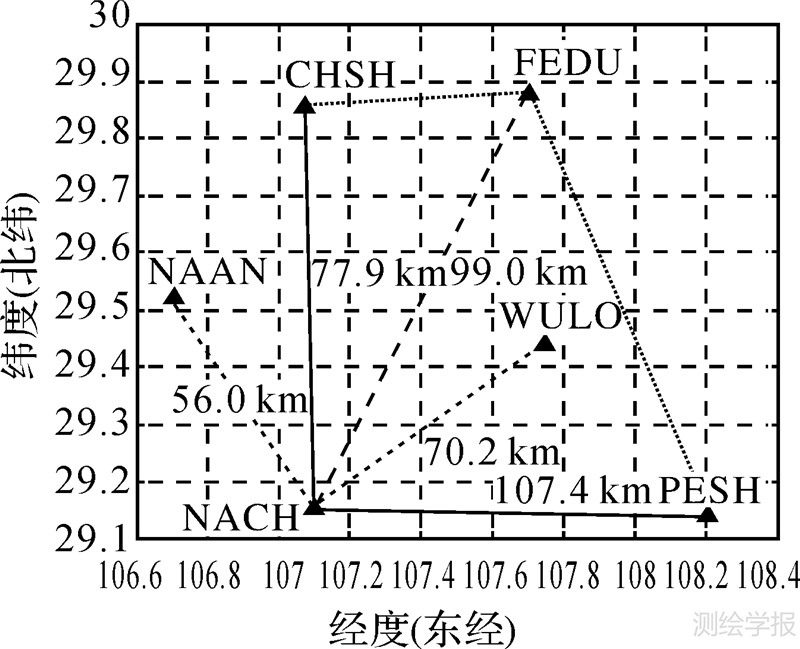
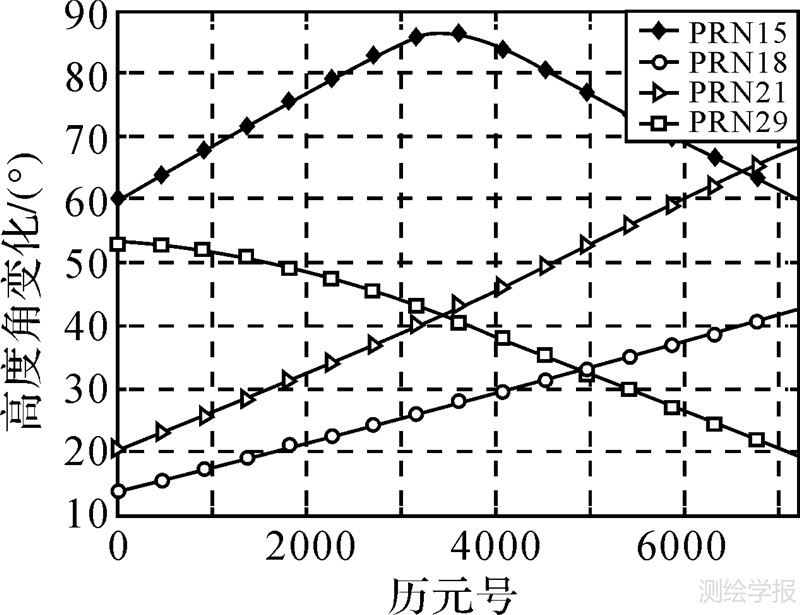
并假设任意改正数满足下式 则对于用户u位置与主参考站n的坐标差(Δxu,n,Δyu,n,Δhu,n)的对流层改正数,可通过建立以下内插模型 并在LCM模型上[16]添加高程因子h,设其内插系数ai满足以下约束条件 式中,Xr-Xi=(Δxri,Δyri,Δhri)。 5 数据处理试验与分析比较 5.1 星型VRS网络模糊度固定试验与分析采用重庆市国土资源GNSS网(CQCORS)的观测数据进行分析,分别选择南川站(NACH)、南岸站(NAAN)、长寿站(CHSH)、丰都站(FEDU)、彭水站(PESH)、武隆站(WULO)共6个基站,以南川(NACH)作为中心参考站,组成星型VRS网络,如图 7所示。该网络中所有参考站均使用天宝天线TRM55971和参考站型接收机。试验数据采用2010-11-10T 10:00:00—11:59:59;采样间隔1 s。根据图 8所示的高度角变化图,选择高度角最大的PRN15卫星作为参考卫星。选择3个代表低、中、高高度角卫星与PRN15组成3组卫星对PRN18-15、PRN21-15、PRN29-15。
|
| 图 7 CQCORS参考站分布图 Fig. 7 Distribution of JSCORS stations |
|
| 图 8 卫星高度角随历元变化图 Fig. 8 The change of elevation of satellites with epochs |
本文主要分析L1双差模糊度的固定。故分别采用单基线解算模式以及本文提出的多基线解算模式进行分析比较。其中单基线解算模式是对星型VRS网络的每一条基线进行模糊度解算。由于单基线模糊度固定时间主要是受较低高度角卫星模糊度收敛的影响,因此以PRN18-PRN15这一卫星对进行分析,其模糊度固定时间结果见表 1所示。
| s | |||||
| 基线 | NACH— NAAN |
NACH— WULO |
NACH— CHSH |
NACH— FUDU |
NACH— PESH |
| 时间 | 282 | 315 | 320 | 427 | 455 |
而多基线解算模式是先选择星型VRS网络中最短基线NACH—NAAN(基线长56 km)进行解算,估计出中心参考站BTJJ的天顶对流层延迟,并将其应用于其余基线,重新构建新的卡尔曼滤波器估计模糊度浮点解与相对天顶对流层延迟。同样以PRN18-PRN15这一卫星对进行分析,其模糊度固定时间结果见表 2所示。
| s | |||||
| 基线 | NACH— NAAN |
NACH— WULO |
NACH— CHSH |
NACH— FUDU |
NACH— PESH |
| 时间 | 282 | 284 | 283 | 301 | 323 |
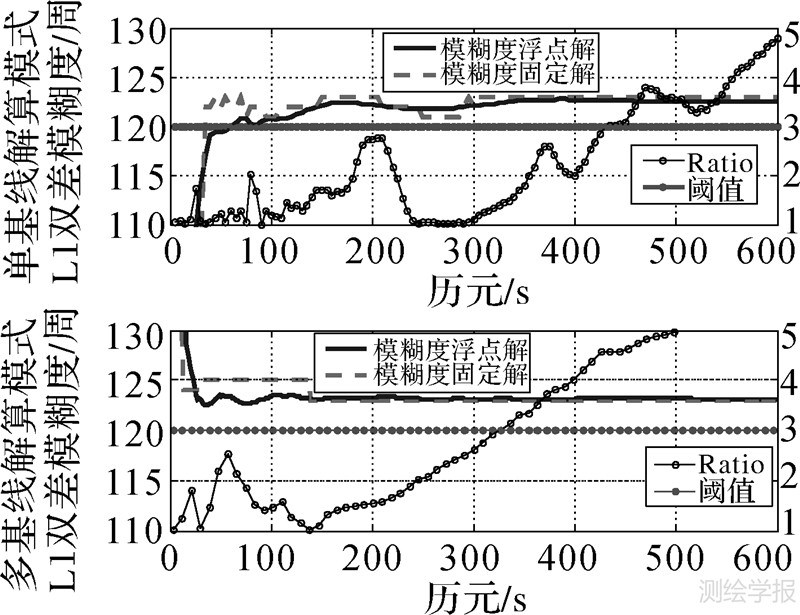
对比表 1和表 2、图 9可以看出,采用本文提出的针对星型解算单元的模糊度解算方式明显比传统VRS的单基线模糊度解算方式优越,它使得模糊度固定时间大大缩短。以基线NACH—PESH为例(如图 9所示),当方差比Ratio因子大于阈值时,可认为模糊度已固定,从图 9可以看出采用多基线解算模式固定速度明显快于单基线解算模式。对比可以看出,采用常规单基线解算模式,随着基线长度的增加,固定时间随之快速增加,而采用星型多基线解算模式,其星型网元内各基线的L1模糊度的固定时间较为接近,有利于提高长距离、大规模网络RTK系统的初始化速度。
|
| 图 9 NACH—PESH两种解算模式比较 Fig. 9 Compare of two resolution models for NACH—PESH |
另外,无论是表 1的结果,还是表 2的结果都表明,长基线L1模糊度固定时间明显长于较短基线。这是由于使用电离层无关组合中,模糊度与相对对流层延迟相关性较强,基线越长,相对对流层延迟越大,其误差也越大,导致长基线上模糊度固定时间很长。
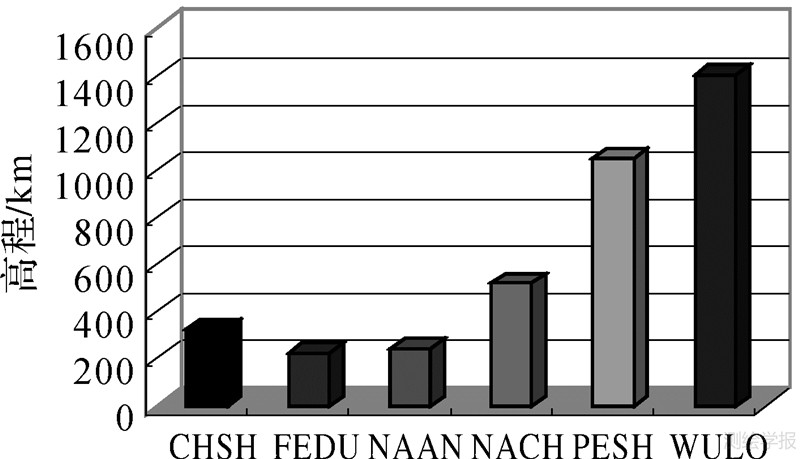
5.2 星型VRS网络改正数计算模型试验与分析试验网络选取同样的星型VRS网络,以NACH作为中心参考站与辅助参考站CHSH、FEDU、PESH组成星型解算单元,以WULO(网内)、NAAN(网外)分别作为流动站,其高程差异分布见图 10,采用本文提出的SIM、SHM分别内插用户电离层改正数、对流层改正数,由于传统的内插模型内插效果基本一致[16],故选择具代表性的线性内插模型LIM,与之进行比较分析。
|
| 图 10 高程差异分布 Fig. 10 Difference of heights among stations |
选取最具代表性的两颗卫星进行分析比较,其中卫星PRN18为低高度角卫星(升星),PRN29为高高度角卫星(降星)。以误差的最大值、平均值、中误差作为统计指标,采用SIM与LIM内插电离层改正数的结果见图 11及表 3,采用SHM与LIM内插对流层改正数的结果见图 12及表 4。

|
| 图 11 LIM与SIM电离层改正数内插误差变化图 Fig. 11 The variation of double-differenced ionospheric biases for LIM and SIM |
| m | ||||||||
| 统计指标 | PRN 18 | PRN 29 | ||||||
| 网外(NAAN) | 网内(WULO) | 网外(NAAN) | 网内(WULO) | |||||
| LIM | SIM | LIM | SIM | LIM | SIM | LIM | SIM | |
| 最大值 | 0.291 | 0.048 | 0.051 | 0.017 | 0.243 | 0.051 | 0.110 | 0.027 |
| 平均值 | 0.084 | 0.015 | 0.012 | 0.005 | 0.045 | 0.013 | 0.020 | 0.006 |
| 中误差 | 0.103 | 0.018 | 0.016 | 0.007 | 0.066 | 0.018 | 0.029 | 0.008 |
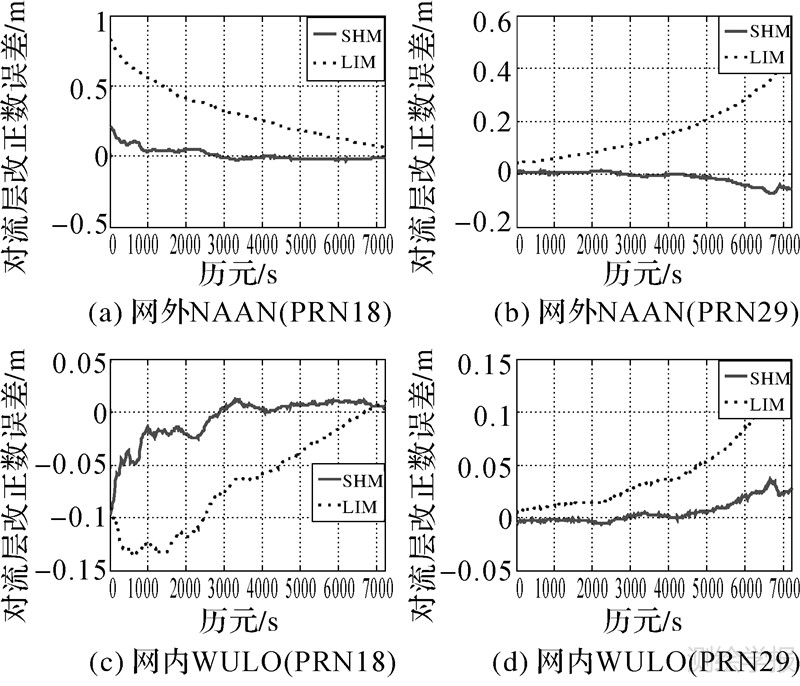
|
| 图 12 LIM与SHM对流层改正数内插误差变化图 Fig. 12 The variation of double-differenced tropspheric biases for LIM and SIM |
| m | ||||||||
| 统计指标 | PRN 18 | PRN 29 | ||||||
| 网外(NAAN) | 网内(WULO) | 网外(NAAN) | 网内(WULO) | |||||
| LIM | SIM | LIM | SIM | LIM | SIM | LIM | SIM | |
| 最大值 | 0.832 | 0.211 | 0.137 | 0.097 | 0.446 | 0.076 | 0.130 | 0.035 |
| 平均值 | 0.318 | 0.032 | 0.068 | 0.015 | 0.166 | 0.013 | 0.044 | 0.008 |
| 中误差 | 0.370 | 0.048 | 0.081 | 0.022 | 0.198 | 0.017 | 0.056 | 0.012 |
从图 11及表 3可以看出,无论流动站是在网内还是网外,本文提出的SIM其内插精度一般在1 cm左右,明显高于传统的LIM内插精度;当在网外时,传统的LIM内插模型改正精度大幅下降,而SIM则下降不明显,仍然保持在1 cm左右。此外网内的内插精度都要高于网外的内插精度,当卫星高度角较低时,传统的LIM内插精度远远低于本文提出的SIM模型,而高度角对SIM模型影响较小,SIM模型内插精度很稳定。
从图 12及表 4可以看出,无论是对于低高度角卫星还是高高度角卫星,本文提出的SHM模型远远高于传统的LIM模型,特别是对于低高度角卫星,LIM模型精度远远低于SHM模型的内插精度;此外可以看出对卫星高度角较高的卫星以及网内流动站内插时,其内插精度较高。
6 结 论试验表明本文提出的星型VRS网络多基线解算模式较传统VRS单基线解算模式效率更高。由于星型VRS网络改正数计算模型的灵活性,本文提出的试验结果表明针对流动站电离层改正数生成的高精度星型内插模型SIM精度优于传统模型,其内插精度稳定在1 cm左右,而对流层改正数三维内插模型SHM可修正参考站与流动站高程差异引起的对流层误差改正数中系统偏差的影响,其内插精度可保持在2 cm左右,明显优于传统内插模型。
| [1] | LANDAU L,VOLLATH U,CHEN X M.Virtual Reference Station Systems[J].Journal of Global Positioning Systems.2002,1(2):137-143. |
| [2] | TRIMBLE.Trimble Virtual Reference Station VRS[M].Sunnyvale:[s.n.] ,2001. |
| [3] | HUANG Dingfa,LI Chenggang,WU Yaoqiang,et al.Study of the Real-time Network Correction Generation[J].Acta Geodaetica et Cartographica Sinica,2007,36(3):256-261.(黄丁发,李成钢,吴耀强,等.GPS/VRS实时网络改正数生成算法研究[J].测绘学报,2007,36(3):256-261.) |
| [4] | KE Fuyang,WAND Qing,PAN Shuguo,et al.Key Algorithm and Technique of VRS Network RTK and Precision Analysis[J].Journal of Astronautics,2009,30(3):1287-1292.(柯福阳,王庆,潘树国,等.VRS网络RTK关键算法与技术及精度分析[J].宇航学报,2009,30(3):1287-1292.) |
| [5] | JENSEN A B O,CANNON M E.Performance of Network RTK Using Fixed and Float Ambiguities[C] //Proceedings of the 2000 National Technical Meeting of the Institute of Navigation.Anaheim:The Institute of Navigation,2000:797-805. |
| [6] | CHEN X M,HAN S W,RIZOS C,et al.Improving Real-time Positioning Efficiency Using the Singapore Integrated Multiple Reference Station Network (SIMCORSN)[C] //Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation. Salt Lake City:The Institute of Navigation,2000:9-18. |
| [7] | HU G,ABBEY DA,CASTLEDEN N,et al.An Approach for Instantaneous Ambiguity Resolution for Medium to Long-range Multiple Reference Station Networks[J].GPS Solution,2005,9(1):1-11. |
| [8] | PAN Shuguo,WANG Qing,KE Fuyang,et al.Method for Integer Ambiguity Resolution in GPS Network RTK[J].Journal of Southeast University:English Edition,2009,25(4):491-495. |
| [9] | GAO Xingwei,LIU Jingnan,GE Maorong.An Ambiguity Searching Method for Network RTK Baselines between Base Stations at Single Epoch[J].Acta Geodaetica et Cartographica Sinica,2002,31(4):305-309.(高星伟,刘经南,葛茂荣.网络RTK基准站间基线单历元模糊度搜索方法[J].测绘学报,2002,31(4):305-309.) |
| [10] | ZHOU Letao,HUANG Dingfa,YUAN Linguo,et al.A Kalman Filtering Algorithm for Online Integer Ambiguity Resolution in Reference Station Network[J].Acta Geodaetica et Cartographica Sinica,2007,36(1):37-42.(周乐韬,黄丁发,袁林果,等.网络RTK参考站间模糊度动态解算的卡尔曼滤波算法研究[J].测绘学报,2007,36(1):37-42.) |
| [11] | HU G R,KHOO H S,GOH P C,et al.Development and Assessment of GPS VRS for RTK Positioning[J].Journal of Geodesy,2003,77(5-6):292-302. |
| [12] | TANG Weiming,LIU Jingnan,LIU Hui,et al.A Modified Combined Bias Interpolation Method for GNSS Network RTK[J].Geomatics and Information Science of Wuhan University,2007,32(12):1156-1159.(唐卫明,刘经南,刘晖,等.一种GNSS网络RTK改进的综合误差内插方法[J].武汉大学学报:信息科学版,2007,32(12):1156-1159.) |
| [13] | ZOU R,LIU H,YAO Y B,et al.Application of Delaunay Triangulated Networks to Continuous Operational Refe-rence System[J].Journal of Geomatics,2005,30(6):9-11.(邹蓉,刘晖,姚宜斌,等.Delaunay三角网构网技术在连续运行卫星定位服务系统中的应用[J].测绘信息与工程,2005,30(6):9-11.) |
| [14] | ZHOU Letao,HUANG Dingfa,LI Chenggang,et al.Algorithm for GPS Network Construction Based on Spherical Delaunay Triangulated Irregular Network[J].Journal of Southwest Jiaotong University,2007,42(3):380-383.(周乐韬,黄丁发,李成钢,等.基于球面Delaunay三角网的GPS网构造算法[J].西南交通大学学报,2007,42(3):380-383.) |
| [15] | LI Chenggang.Generation and Distribution Technique of Precise Differential Corrections for GPS/VRS Network[D].Chengdu:Southwest Jiaotong University,2007.(李成钢.网络GPS/VRS系统高精度差分改正信息生成与发布研究[D].成都:西南交通大学,2007.) |
| [16] | LI Chenggang,LI jie,YANG Li,et al.Ionospheric Disturbance Delay Correction Method for Reference Station Network over Mid&Low Latitude Region[J].Science of Surveying and Mapping,2009,34(4):27-29.(李成钢,李杰,阳力,等.中低纬度地区连续运行参考站网络电离层扰动修正技术研究[J] ,测绘科学,2009,34(4):27-29.) |
| [17] | DAI Liwen,HAN Shaowei,WANG Jinling,et al.A Study on GPS/GLONASS Multiple Reference Station Techniques for Precise Real-time Carrier Phase-based Positioning[C] //Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation. Salt Lake City:ION Publications Department,2001:392-403. |