2. 南京师范大学 地理科学学院,江苏 南京 210097
2. School of Geographic Science, Nanjing Normal University, Nanjing 210097, China
1 引 言
DEM精度是评价空间数据质量的重要指标,目前DEM精度评价指标大多使用中误差、标准差等一系列统计指标,其评价方式采用参考点法,即用有限个更高精度的参考点,通过计算参考点处误差的统计量来评价整幅DEM精度。统计量精度指标从整体意义上描述了DEM和参考值的离散程度,而无法给出DEM误差的空间分布特征。随着新型传感器如激光扫描、干涉雷达和摄影测量等一系列的地形数据获取方式的应用和推广,迫切需要对DEM各类误差进行精细化描述,以便为DEM数字地形分析和应用的不确定性分析提供理论支撑。
本文主要针对传统的两类DEM误差(噪声误差和逼近误差)进行分析和建模。DEM精度模型研究的核心问题是两类误差的定量化描述。经过长期研究,国内外围绕这个问题提出了众多模型,主要分为经验模型和理论模型。经验模型主要通过大量数据试验和统计分析,建立DEM精度与其相关量(如地形起伏度、曲率等)之间的函数关系,实现对DEM格网精度的评价。理论模型通常先对自然地表做数学假设,形成“概念地表”,进而利用特定的数学理论建立DEM误差的数学模型,根据所采用的数学理论不同可以分为解析方法[1, 2, 3]、模糊方法[4, 5]、分形方法[6, 7, 8, 9]和统计方法[10, 11, 12]等。这些方法在很大程度上能给出DEM局部误差可靠预测。然而,由于DEM构建方法的千差万别,现有的方法仍存在一些问题:① 已有模型往往仅考虑单一误差的预测,没有对两类误差实现统一描述;② 已有的模型多数针对于特定的DEM插值建模方法,适用性较差。本文利用空间统计和误差传播等相关理论,建立基于随机过程的格网DEM精度场模型,实现任意插值方式下的格网DEM格网点精度的定量化描述,并结合格网DEM生产实际,对DEM精度场模型进行试验分析和验证。 2 格网DEM精度场模型 2.1 DEM精度场
规则格网DEM结构模型通常用矩阵表示,设其行列号数为m、n,其数学描述为
DEM精度场是指一幅存储对应DEM的每个格网精度的矩阵序列,其行列数、格网大小以及坐标系统与对应的DEM一致,其数学描述为
为实现DEM数据的格网化,需要对观测数据进行插值或重采样。如图 1所示,设有待插值点Pi(xi,yi,zi),插值表面与观测点之间的误差包含两部分,一部分由于观测点上存在的观测误差经插值函数传播到插值表面上,产生DEM噪声误差Δi;另一部分是由于DEM重构而造成DEM表面与真实地表之间的高程偏差而产生的逼近误差εi(也称为地形描述性误差[1])。当对所有格网进行插值生成DEM时,所有的噪声误差Δi和逼近误差εi的方差就组成DEM精度场,分别称之为DEM噪声精度场和DEM逼近精度场。

|
| 图 1 DEM精度场示意图 Fig. 1 The sketch of DEM accuracy fields |
设Z(x1),Z(x2),…,Z(xn)是联合分布的随机变量,x1,x2,…,xn是空间采样点的空间位置,h为位置偏移,如果Z(x1),Z(x2),…,Z(xn)的联合分布与Z(x1+h),Z(x2+h),…,Z(xn+h)的联合分布相同,那么就说明变量Z是平稳的。平稳条件通常比较严格,实际应用中只使用二阶平稳假设[13]:① 随机变量的均值不随位置x而变化;② 协方差函数Cov[Z(x),Z(y)]只取决于样本点x和y之间的距离‖x-y‖。地形作为区域化变量,其数字表现形式(DEM)绝大多数是非平稳的,其变异性可由3部分来表示:确定性部分t、相关信号部分s和随机噪声部分n[13, 14]。其中确定性部分t代表地形的整体趋势,相关信号部分s表示地形起伏在空间上自相关性,随机噪声n表示具有特定统计性质的随机干扰量,因此DEM高程变量可以表示为
设某次插值过程有n个已知点,其高程向量为z=[z1 z2 … zn],设s=[s1 s2 … sn]表示已知点信号向量,t=[t1 t2 … tn]表示已知点的趋势向量,n=[n1 n2 … nn]为观测点上的噪声向量。设待插点P的高程为zp,其信号量、趋势量和随机噪声分别为s′、t′、n′,根据公式(3),zp、z可以表示为
根据插值原理,待插点zp的估计值 p可表示为已知点z=[z1 z2 … zn]的线性函数[15]
p可表示为已知点z=[z1 z2 … zn]的线性函数[15]
用矩阵可表示为
考虑到待插点P为非观测量,其噪声误差为n′为0,因此估计误差为
于是估计误差v的方差为
考虑到噪声误差n′、n与信号s′、s相互独立,且信号与噪声的期望均为0,即E(s′)=E(s)=E(n)=0,趋势t′、t以及m均为常量,对式(9)整理可得
式(10)右边的第1项和第2项表示DEM逼近误差方差(记为Dε),第3项是噪声误差方差(记为DΔ),其中逼近精度又分为两部分,第1项代表趋势精度部分(记为Dεt),表示趋势面的逼近精度,第2项表示信号精度(Dεs),表示空间相关部分精度。当m=0且已知采样点不具有趋势时,趋势误差为0;设Ds′、Dss′、Ds′s、Ds分别代表待插点,已知点与待插点,待插点与已知点,已知点之间信号的协方差阵,由于已知点上的噪声误差相互独立且方差σi2(i=1,2,…,n),即已知点上的先验协方差阵Dn=diag(σ12,σ22,…,σn2),则式(10)可分解为以下3项
以上进一步证明DEM误差是噪声误差和逼近误差之和,而逼近误差又包含趋势面逼近误差和信号逼近误差。 2.3 信号量的方差与协方差阵
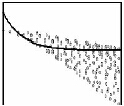
为计算公式(11)中信号量的协方差阵Ds′、Dss′、Ds′s、Ds,需要确定已知点之间以及已知点与待插点之间的协方差函数。与半变异函数γ(d)相对应,协方差函数C(d)通常是距离单调递减的函数(如图 2),其参数主要包括有效变程a、偏基台C1和块金C0。

|
| 图 2 半变异函数和协方差函数 Fig. 2 Semivariance and covariance function |
常用的经验协方差函数类型较多,由于协方差函数模型的类型对DEM精度影响并不大[16, 17],本文统一采用指数协方差函数模型,其表达式为
协方差函数参数估计采用多项式回归方法,首先计算全部点对之间的高程方差,并按照两点之间的距离进行分组统计,计算每组高程的平均方差,最后依据最小二乘方法对各组平均方差进行多项式拟合,解算公式(12)中的a、C1和C0参数。
确定了信号量的协方差函数C(d),因此观测点和待插点信号之间的方差和协方差阵即可用协方差函数表示,于是DEM精度场模型如下
2.4 模型计算流程综上所述,本文的精度场模型计算过程如下。
(1) 获取已知点先验精度:已知数据通常来自于直接观测数据或者间接数据,其高程精度由数据生产单位提供。
(2) 趋势面分析:通过考察不同次数的趋势面的协方差云图和误差方差,确定趋势面的次数,然后利用多项式回归方法确定趋势面方程的参数。
(3) 协方差函数拟合:源数据去掉趋势后,对已知点的点对之间的距离进行分组,分别计算每组数据的平均方差,然后利用多项式回归解算协方差函数的参数。
(4) 权重向量计算:确定具体的插值类型和插值参数,若为基于TIN的插值,首先需要构建TIN,其他类型插值直接进行插值计算,计算并记录式(5)中的权重向量k。
(5) 计算DEM精度场:按式(13)计算每个插值格网的方差,获得DEM精度场数据,并计算DEM精度场的统计信息。
计算方法的流程图如图 3所示。

|
| 图 3 DEM精度场计算流程 Fig. 3 Flow chart of DEM accuracy calculation |
试验采用地形图数据,选择山西省雁北地区山阴县1∶10 000地形图数据(图 4),包括高程注记点、等高线和内业加密点,并构建不规则三角网。研究区域属于平原地区,平均高程1 013.5 m,平均坡度0.2°,其中高程注记点231个,等高线15条,内业加密点22 489个。
本次试验依据国家由地形图生产格网DEM流程,即以等高线为约束线对高程注记点和内业加密点建立约束不规则三角网,再对不规则三角网插值生成格网DEM,使用插值方法为TIN的线性插值。本次试验构建不规则三角网(图 4(d)),三角形顶点数为38 794,三角形数为77 553。

|
| 图 4 地形数据 Fig. 4 Topographic data |
依据国家地形图高程精度标准(GB/T13977),对于平原区1∶10 000等高线的高程精度是0.5 m,高程注记点精度0.35 m,内业加密点的精度采用丘陵地精度标准,即1.0 m。
通过对试验数据进行协方差函数拟合,分别得到4种协方差函数和协方差云图(表 1),比较协方差云图可知三次曲面的协方差云图更收敛且中误差最小,因此选用三次曲面作为本试验样区的趋势面,其对应的协方差函数的表达式为
式中,e为自然对数常数;d为水平距离。
经过计算,获得TIN线性插值的规则格网精度场数据(图 5),包括噪声精度场、逼近精度场的趋势部分、逼近精度场的相关部分,以及最终叠加获得合成精度场。

|
| 图 5 DEM精度场 Fig. 5 DEM accuracy fields |
对精度场数据的进行统计分析(精确到0.001 m),获得精度场数据的最小值、最大值、平均值和标准差,如表 2所示。
| 精度场 | 最小值 | 最大值 | 平均值 | 标准差 |
| DΔ场 | 0.146 | 1 | 0.4 | 0.156 |
| Dεt场 | 0 | 0.113 | 0 | 0.001 |
| Dεs场 | 0 | 0.216 | 0.032 | 0.02 |
| α场 | 0.151 | 1 | 0.427 | 0.153 |
对表 2中的统计值进一步分析并结合图 5发现,从误差分布情况来看,逼近精度场在已知点附近的精度值较低,而在其他地方的精度值较高,表明已知点、等高线附近逼近精度较高,这符合插值条件下逼近误差的特征;噪声精度场刚好相反,在已知点、等高线附近的值较高,在其他地方较低。比较不同精度场数据的统计值发现,噪声误差占DEM总体误差的很大一部分,其主要原因是平原样区的协方差函数的偏基台值较低,其逼近精度较高,因此在平原地区的DEM精度评价中不能忽略源数据的误差,这与实际情况吻合。 4 结 论
借助空间统计和误差传递等相关理论,严密推导DEM格网精度的数学公式,证明DEM精度是数据精度和逼近精度之和,即DEM精度场可以分解成逼近精度场和噪声精度场,而逼近精度场又可以分解为趋势的逼近精度和相关量的逼近精度。在对地形起伏的随机平稳假设条件下,DEM两类误差的统计性质具有统一性,都属于随机误差。从试验结果看出,DEM精度评价应该从数据精度和逼近精度两方面加于考虑,忽略其中之一都不能得到DEM可靠的精度估计。DEM精度场数据对于DEM数据质量评价,以及基于DEM的数字地形分析不确定性研究具有重要意义,主要表现在以下两点:首先,根据DEM精度场数据,可以评价数字地形分析的算法的传递误差,分析地形因子的抗误差能力;其次,根据DEM精度场数据可以更加清晰描绘DEM误差的空间相关性规律,而DEM误差空间相关性已经被证明存在并极大影响DEM数字地形分析的不确定性。DEM精度场模型将为DEM提供更加全面的精度描述信息,进一步完善DEM的误差分析体系,为DEM的地形分析及应用的安全性和可靠性分析提供理论支撑;同时本研究也为其他类型空间数据的不确定性研究、地学模型的可靠性分析提供了有益的参考。
| [1] | TANG G. A Research on the Accuracy of Digital Elevation Models [M]. Beijing: Science Press, 2000. |
| [2] | LI Zhilin, ZHU Qing. Digital Elevation Model [M]. Wuhan: Press of Wuhan Technical University of Surveying and Mapping, 2003.(李志林,朱庆.数字高程模型 [M].武汉:武汉测绘科技大学出版社,2003.) |
| [3] | KRAUS K. Principle and Practice on Photography Processing System [M]. LI Deren, Translate. Beijing: Surveying and Mapping Press , 1989. (KRAUS K.摄影测量信息处理系统的原理与实践[M].李德仁,译.北京:测绘出版社,1989.) |
| [4] | ZHANG Jingxiong, DU Daosheng. A Fuzzy Field Approach to Mapping ε-error Band Models[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1997, 22(3): 212-215.(张景雄,杜道生.基于模糊场的ε误差带模型[J].武汉测绘科技大学学报,1997,22(3):212-215.) |
| [5] | SANTOS J, LODWICK W A,NEUMAIER A. A New Approach to Incorporate Uncertainty in Terrain Modeling [C]//Proceedings of the Second International Geographical Information Science Conference. Berlin: Springer, 2002: 291-299. |
| [6] | POLIDORI L, CHOROWICA J, GUILLANDE R. Description of Terrain as a Fractal Surface and Application to Digital Elevation Model Quality Assessment [J]. Photogrammetric Engineering and Remote Sensing, 1991, 57(10): 1329-1332. |
| [7] | BROWN D, BARA T. Recognition and Reduction of Systematic Error in Elevation and Derivative Surface from 7.5-minute DEMs [J].Photogrammetric Engineering and Remote Sensing, 1994, 60(2): 189-194. |
| [8] | LI Shuang , YAO Jing. Research on DEM Uncertainty Using Fractals Method [M]. Beijing: Science Press, 2007.(李爽,姚静.基于分形的DEM数据不确定性研究[M].北京:科学出版社,2007.) |
| [9] | WANG Guangxia, CUI Kai , DAI Jun. The Accuracy Evaluation of DEM Based on Fractal Analysis [J]. Journal of Institute of Surveying and Mapping, 2005, 22(2): 107-109.(王光霞,崔凯,戴军.基于分形的DEM精度评估[J].测绘学院学报,2005,22(2):107-109.) |
| [10] | KUBIK K, BOTMAN A. Interpolation Accuracy for Topographic and Geological Surfaces [J]. ITC Journal, 1976,2:236-274. |
| [11] | CLERICI E,KUBIC K. Theoretical Accuracy of Terrain Interpolation[M]//XUE Shungui, Translate.Proceedings on Photogrammetric Auto Digitalization. Beijing: Surveying and Mapping Press, 1974. (CLERICI E, KUBIC K.地形地表插值法的理论精度[M]//薛顺贵,译.摄影测量自动数字化译文汇编.北京:测绘出版社,1974.) |
| [12] | HUNTER G J ,GOODCHILD M F. Dealing with Error in a Spatial Database:a Simple Case Study [J]. Photogrammetric Engineering and Remote Sensing, 1995, 61:529-537. |
| [13] | ZHANG R. Theory and Application on Spatial Variation [M]. Beijing: Science Press, 2005. (张仁铎.空间变异理论及应用[M].北京:科学出版社,2005.) |
| [14] | JOHNSTON K, VER HOEF J M, KRIVORUCHKO K, et al. Using ArcGIS Geostatistical Analyst [M]. Redlands: ESRI, 2001. |
| [15] | LU Huaxing. Research on DEM Error Model [D]. Nanjing: Nanjing Normal University,2008.(卢华兴. DEM误差模型研究[D].南京:南京师范大学,2008.) |
| [16] | OKSANEN J. Digital Elevation Model Error in Terrain Analysis [D]. Hesinki:University of Hesinki,2006. |
| [17] | LIU Xuejun, BIAN Lu, LU Huaxing, et al. The Accuracy Assessment on Slope Algorithms with DEM Error Spatial Autocorrelation [J]. Acta Geodaetica et Cartographica Sinica, 2008, 37 (2):200-206 .(刘学军,卞璐,卢华兴,等.顾及DEM误差自相关的坡度计算模型精度分析[J].测绘学报,2008,37 (2):200-206.) |