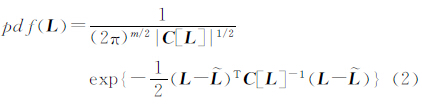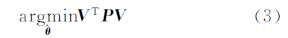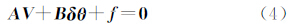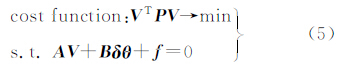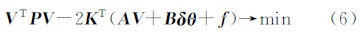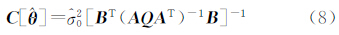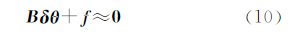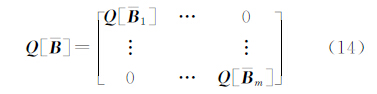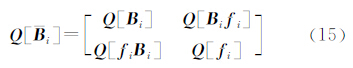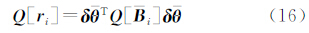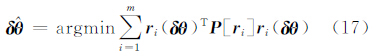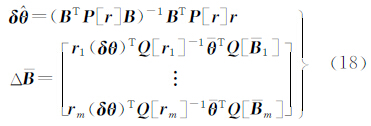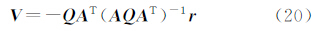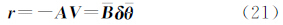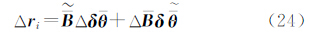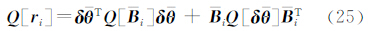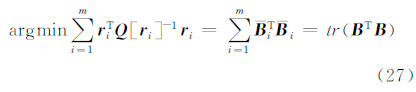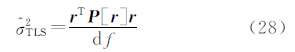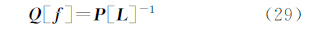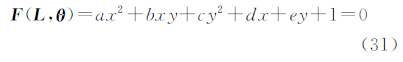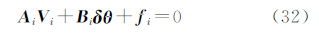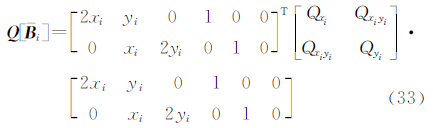2. 中南大学 地球科学与信息物理学院,湖南 长沙 410083
1 引 言
经典测量平差方法是假设观测误差服从正态分布,以观测值的加权最小二乘条件为目标函数,以观测值与参数之间的函数模型线性化为约束条件,并根据约束条件的不同形式得到各种平差模型。文献[1]于20世纪80年代提出了统一的平差模型——附限制条件的条件平差法,经典摄影测量平差理论均以此模型为基础。由于附限制条件的条件平差问题解算较复杂,目前诸多测量平差软件和理论大多以间接平差模型为基础,现代测量平差与数据处理理论仍然是以高斯-马尔可夫模型为核心,通过该模型在不同层面上的扩充、发展形成的若干新理论、新方法[2, 3]。近年来虽然出现了一些扩展模型,但应用上仍相对较少[4, 5, 6]。近年来,国内外许多学者采用总体最小二乘(total least squares,TLS)估计方法解算诸如曲线拟合、坐标变换等问题[7, 8, 9, 10]。TLS法是文献[11]于1980年提出的对线性变量含误差(errors-in-variables,EIV)模型的参数估计方法,该方法考虑了系数矩阵的误差,是一种不同于经典测量平差原理的新方法。文献[12]从理论上证明:对于Y≈Dθ(Y、D分别表示含误差的系数矩阵,θ表示待估计参数)的线性EIV模型,当增广系数矩阵[D Y]的所有元素均服从独立等精度分布时,TLS方法与经典最小二乘的估计结果一致。但这种假设在实际应用中往往不成立,因此需要采用加权总体最小二乘方法(weighted total least squares,WTLS)。由于实际问题中系数矩阵元素间的方差关系极为繁杂且难以准确求定,文献[13]根据系数矩阵权的结构将加权总体最小二乘问题简化为:广义TLS方法、按元素独立 (element-wise) 的WTLS方法、按列独立 (column-
wise) 的WTLS方法、按行独立(row-wise)的WTLS方法等,在已有的应用中往往采用简化权结构或等价权[14, 15, 16]方法解决具体问题。而许多包含不等精度观测值的EIV模型如曲线拟合、坐标变换、直接线性变换等可近似假定条件方程间独立或分块独立,从而简化为RWTLS问题。本文以按行独立的EIV函数模型为背景,给出了利用RWTLS方法和附参数的条件平差方法在解决该问题的原理和解算方法,证明二者的平差结果是一致的,最后以两个典型实例验证。 2 附未知参数的条件平差模型及其解法对于经典测量平差问题,设观测值的总个数为m,必要观测数为t,此时多余观测数r=m-t,若引入u个独立的参数,可以列出c=r+u个条件方程式,用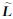 ∈Rm×1表示观测值真值,
∈Rm×1表示观测值真值,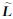 ∈Ru×1表示参数,函数模型可表示为
∈Ru×1表示参数,函数模型可表示为
由于观测值有误差,从而导致参数也含有误差,因而也称为EIV模型[11]。设观测值L=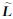 +Δ(L表示观测值,Δ表示误差),测量平差的目的就是找到最佳估计值
+Δ(L表示观测值,Δ表示误差),测量平差的目的就是找到最佳估计值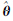 。经典测量平差理论以Δ服从数学期望为零的正态分布为前提,以C[L]∈Rm×m表示观测值的协方差阵,L的概率密度函数为
。经典测量平差理论以Δ服从数学期望为零的正态分布为前提,以C[L]∈Rm×m表示观测值的协方差阵,L的概率密度函数为
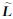 未知,Δ也无法获取,用
未知,Δ也无法获取,用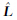 表示观测值的估值,V表示观测值改正数,二者之间的关系为:
表示观测值的估值,V表示观测值改正数,二者之间的关系为: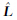 =L+V,在有多余观测值的情况下,参数
=L+V,在有多余观测值的情况下,参数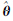 的最大似然估计等价于最小二乘估计[1]
式中,P表示观测值的权阵,与协方差阵的关系为σ02P-1=C[L](σ02表示单位权方差),Q=P-1称为协因数阵。经典测量平差问题是以式(3)为目标函数,以式(1)为约束条件的最优化问题。令
的最大似然估计等价于最小二乘估计[1]
式中,P表示观测值的权阵,与协方差阵的关系为σ02P-1=C[L](σ02表示单位权方差),Q=P-1称为协因数阵。经典测量平差问题是以式(3)为目标函数,以式(1)为约束条件的最优化问题。令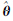 =θ0+δθ(θ0表示初值,δθ表示初值与估值之间的差值),同时考虑观测值和参数的误差,将式(1)线性化,得到其一般形式为
式中
=θ0+δθ(θ0表示初值,δθ表示初值与估值之间的差值),同时考虑观测值和参数的误差,将式(1)线性化,得到其一般形式为
式中
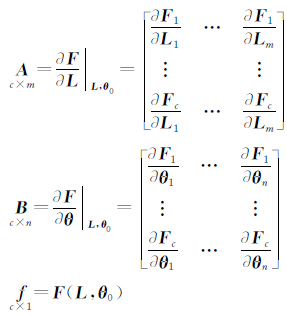
综合式(3)、式(4)得到附参数的条件平差模型
式(5)是一个求条件极值问题,按拉格朗日乘数法求条件极值的原理
式中,K∈Rc×1表示联系数,将上式分别求V、δθ、K偏导并令其等于0,得到[1]根据误差传播定律得到参数的协方差阵为
用df表示自由度,在经典测量平差问题中等于多余观测数,即df=r=c-u,单位权中误差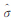 02为
02为
简单总体最小二乘问题通常可表示为求解一个Y≈Dθ形式的超定方程,若在函数模型中引入全部参数,此时u=t,条件方程个数c=r+u=m,即条件方程的个数等于观测值的个数,若只考虑参数的误差,将式(1)在参数初值处线性化,式(4)可写成
此时,B∈Rm×n;δθ∈Rn×1;f∈Rm×1。由于m≥n,因此求解δθ的问题是一个求解超定方程解的问题。仅考虑f的误差,在ΔfTΔf→min准则下的估计称为简单最小二乘估计,同时考虑B和f的误差在tr(ΔBTΔB)+ΔfTΔf→min准则下的参数估计称为简单TLS估计,得到的参数分别为[11]令 =[B f]∈Rm×(n+1),δ
=[B f]∈Rm×(n+1),δ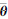 =[δθT 1]T∈R(n+1)×1,σn+1为
=[δθT 1]T∈R(n+1)×1,σn+1为 T
T 的最小特征值。将
的最小特征值。将 T
T 进行奇异值分解,即
进行奇异值分解,即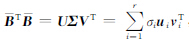 ,δ
,δ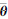 的解为
的解为 T
T 最小特征值σn+1对应的右特征向量vn+1,得到
最小特征值σn+1对应的右特征向量vn+1,得到
简单TLS估计假设矩阵 的所有元素均服从独立等精度分布,而在实际应用中
的所有元素均服从独立等精度分布,而在实际应用中 的元素包含许多常数,其方差等于0,而对于非常数元素,其方差可能不相等和相关,从而导致简单TLS估计非最优估计,需要加权。用Q[
的元素包含许多常数,其方差等于0,而对于非常数元素,其方差可能不相等和相关,从而导致简单TLS估计非最优估计,需要加权。用Q[ ]∈Rm(n+1)×m(n+1)表示
]∈Rm(n+1)×m(n+1)表示 的协因数阵,加权总体最小二乘问题可表示为
的协因数阵,加权总体最小二乘问题可表示为
 ]-表示Q[
]-表示Q[ ]的广义逆矩阵;Δ
]的广义逆矩阵;Δ 表示
表示 的改正值;vec(·)将表示将矩阵元素按行排列得到的向量,由于
的改正值;vec(·)将表示将矩阵元素按行排列得到的向量,由于 可能包含常数从而导致Q[
可能包含常数从而导致Q[ ]大多奇异,不便于求解。为了简化计算,假设
]大多奇异,不便于求解。为了简化计算,假设 按行独立,此时的WTLS问题可简化为按行独立的TLS问题,
按行独立,此时的WTLS问题可简化为按行独立的TLS问题, 的协因数阵是一个分块对角阵
式中,Q[
的协因数阵是一个分块对角阵
式中,Q[ i]∈R(n+1)×(n+1)表示第i行元素的协因数阵,由于
i]∈R(n+1)×(n+1)表示第i行元素的协因数阵,由于 i=[Bi fi],其形式为
i=[Bi fi],其形式为
文献[11]将WTLS的解算分成两个计算步骤,简化为求解一个无约束条件的极值问题,用数值迭代计算来实现。其核心思想是不直接求系数矩阵每个元素的改正值,而是先假定参数固定,仅考虑系数矩阵的方差,经误差的线性传播得到残差的方差,用残差的加权最小二乘代替系数矩阵元素的加权最小二乘,得到参数的估值,然后进一步求出系数矩阵元素的改正值,经迭代直至收敛。令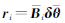 表示残差,若不考虑参数的误差,残差的协因数阵为
表示残差,若不考虑参数的误差,残差的协因数阵为
若要进一步求观测值的改正数,顾及式(5)、式(10)得到
根据式(19)无法得到V的唯一解,根据最小二乘准则VTPV=min(P=Q-1表示观测值的权阵),相当于经典条件平差问题,得到观测值的改正数[1]
4 一致性证明及分析由式(5)和式(10)得到以下关系
根据误差传播定律,得到残差协因数阵的表达式应为
在总体最小二乘方法中,由于不求Ai,此时残差的误差不宜采用式(22)计算,若用上标“~”表示真值,则残差与系数矩阵和观测值之间的关系表示为
忽略高次项,得到真误差之间的关系
按误差传播定律,不考虑δ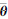 和
和 间的相关性,得到残差协因数阵的表达式
间的相关性,得到残差协因数阵的表达式
在数值计算过程中,通常先考虑其中的一项误差,即固定参数或固定系数矩阵,通过迭代方法实现。在经典间接平差模型中,是不考虑系数矩阵的误差,先求出参数的改正值后再更新系数矩阵然后进行下一次迭代。而在总体最小二乘迭代算法中固定参数值,得到残差的近似协因数阵后再求参数,然后迭代。若采用式(22)计算残差的方差并假设各行独立,得到残差向量的协因数阵为 ,顾及
,顾及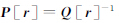 ,代入式(18)得到
,代入式(18)得到
式(26)与式(7)的解析表达式相同,从而证明RWTLS与附参数的条件平差法的结果一致。若不采用式(22)计算残差的方差而按式(16)计算,由于满足式(21)的线性关系,两种计算方法得到的残差的协因数阵相等。无论是残差的方差还是系数矩阵元素的方差都是由观测值的误差传播得到,均满足误差传播律,因而RWTLS的结果与附参数的条件平差结果一致。下面针对几种特殊情况来说明:
(1) A=I的情况(I为单位矩阵),此时的问题为经典间接平差问题,根据误差传播原理,此时残差的权即为观测值的权,代入两种计算方法的参数表达式,得到的结果一致。
(2) 的情况,此时
的情况,此时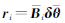 ,
,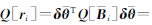 常数,根据RWTLS的解算原理,目标函数为
常数,根据RWTLS的解算原理,目标函数为
此时即为简单总体最小二乘问题,将Q[r]=I代入式(18)中,得到两种方法的计算结果一致,这符合文献[12]的结论,即当系数矩阵 的所有元素均服从独立等精度分布时,TLS方法与经典最小二乘方法的估计结果一致。
的所有元素均服从独立等精度分布时,TLS方法与经典最小二乘方法的估计结果一致。
(3) 精度评定问题,按上述计算原理,RWTLS的单位权中误差的计算式应为
将式(20)、式(22)代入式(9)中可以得到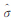 02=
02=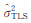 ,但此时的自由度df 应该取整个线性系统的自由度,也就是说两种算法的自由度是相等的。并可以进一步证明,两种方法得到的观测值的改正值、参数的协因数阵也相等。
,但此时的自由度df 应该取整个线性系统的自由度,也就是说两种算法的自由度是相等的。并可以进一步证明,两种方法得到的观测值的改正值、参数的协因数阵也相等。
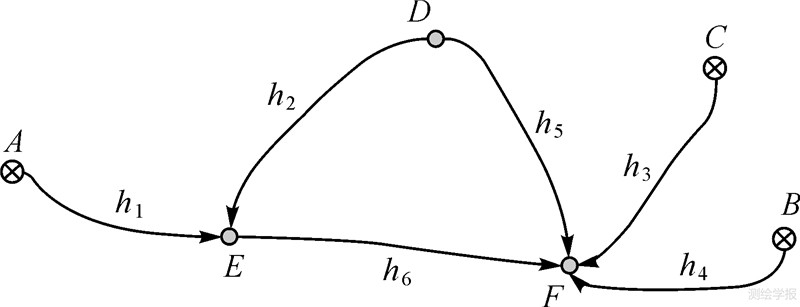
如图 1水准网,其观测值和已知数据见表 1,为保证系数矩阵各行之间不相关,先按经典间接平差方法列出误差方程,观测值的权取路线长度的倒数。然后按下面的计算过程进行加权总体最小二乘解算,计算结果取小数点后5位有效数字,两种方法得到的参数和及其中误差见表 2,数据表明二者的结果是完全一致。
|
| 图 1 水准控制网形 Fig. 1 The configuration of a level control network |
| 测 段 |
观测 值/m |
路线 长/km |
测 段 |
观测 值/m |
路线 长/km |
点 号 |
高程 /m |
| h1 | +1.505 | 3 | h4 | -0.231 | 7 | A | 28.475 |
| h2 | -0.187 | 5 | h5 | +0.756 | 2 | B | 31.118 |
| h3 | -1.582 | 6 | h6 | +0.937 | 1 | C | 32.459 |
| m | |||
| 估计方法 | HE | HF | HD |
| WLS | 29.964 74± 0.010 64 |
30.898 04± 0.010 727 |
30.144 82± 0.014 058 |
| RWTLS | 29.964 74± 0.010 64 |
30.898 04± 0.010 727 |
30.144 82± 0.014 058 |
(1) 先取参数的初值HE=29.980、HF=30.877、HD=30.121。按传统间接平差原理得到误差方程,此时残差等于观测值的改正数:r=Bδθ-f,其中

(2) 按简单TLS方法得到参数初值。
(3) 为了得到残差的协因数阵,先计算f的协因数阵
(4) 得到残差的协因数阵
式中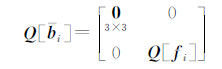
(5) 求出参数,本算例由于残差的误差不受参数影响,不需要迭代。
5.2 最小二乘拟合算例模拟一个常见的二次曲线拟合算例,用椭圆的参数方程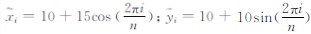 产生10个点(i表示点的序号),并将椭圆沿逆时针方向旋转30°,然后在各点加上真误差Δxi,Δyi~N(0,(0.01i)2)用来模拟不等精度观测值。现按附参数的条件平差方法和RWTLS方法解算该问题,并与参数真值比较。二次曲线的一般方程写为
产生10个点(i表示点的序号),并将椭圆沿逆时针方向旋转30°,然后在各点加上真误差Δxi,Δyi~N(0,(0.01i)2)用来模拟不等精度观测值。现按附参数的条件平差方法和RWTLS方法解算该问题,并与参数真值比较。二次曲线的一般方程写为
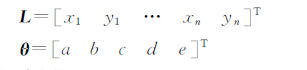

将上面的方程作为约束条件并考虑观测值的权后得到附参数的条件平差的解算结果,由于Ai的系数与参数有关,因此也需要迭代计算。而在进行加权总体最小二乘计算时,需要得到 i的协方差阵,而
i的协方差阵,而 i的协方差阵是观测值传播得到的,其计算式为
i的协方差阵是观测值传播得到的,其计算式为
根据上述计算步骤,取简单TLS的结果为初值,以‖δθ‖<10-8作为迭代结束标志,本算例一般经3~4次迭代即可收敛,模拟1000次,两种方法得到参数及其误差的差值都在10-9数量级以下,说明主要是数值计算误差。表 3是随机选取的一组观测数据,解算结果见表 4(取小数点后6位有效数字),表明估计结果完全一致。
| 像素 | |||
| 点号 | X | Y | 叠加误差 |
| 1 | 13.267 | 29.383 | 0.01 |
| 2 | 1.891 | 29.077 | 0.02 |
| 3 | -8.842 | 22.887 | 0.03 |
| 4 | -14.736 | 13.193 | 0.04 |
| 5 | -13.597 | 3.705 | 0.05 |
| 6 | -6.027 | -2.145 | 0.06 |
| 7 | 5.398 | -1.801 | 0.07 |
| 8 | 16.141 | 4.368 | 0.08 |
| 9 | 22.027 | 14.077 | 0.09 |
| 10 | 20.825 | 23.641 | 0.10 |
| 估计方法 | a | b | c | d | e |
| 真值 | -0.009 773 | 0.005 511 | -0.012 955 | -0.003 741 | 0.333 753 |
| TLS估计 | -0.009 674 | 0.005 396 | -0.012 709 | -0.003 082 | 0.326 639 |
| WLS估计 | -0.009 692 ±0.000 142 |
0.005 463 ±0.000 110 |
-0.012 765 ±0.000 226 |
-0.003 468 ±0.001 194 |
0.328 157 ±0.006 387 |
| RWTLS估计 | -0.009 692 ±0.000 142 |
0.005 463 ±0.000 110 |
-0.012 765 ±0.000 226 |
-0.003 468 ±0.001 194 |
0.328 157 ±0.006 387 |
以上选用了两个比较典型的算例,算例1选用经典间接平差问题并且采用实测数据,由于水准测量的条件方程本身就是线性的,可以避免线性化对估计结果可能造成的影响,计算过程中不需要迭代。第2个算例选择曲线拟合问题,采用不等精度的模拟数据,并采用迭代方法来求解,两个算例得到的参数值及其方差完全一致。结合前面的理论分析可知:加权总体最小二乘与经典附参数的条件平差是同一模型的两种不同解法。附参数的条件平差法以一个等式条件为约束,以原始观测值的加权最小二乘条件为目标函数,加权总体最小二乘是以加权增广系数矩阵的最小二乘条件为目标函数,以一个齐次线性方程为约束条件,而在计算中,将每行元素的改正数和对应的方差转换为等价的残差和对应的权,而这些误差均是由观测值的误差传播得来的,因而估计结果是一致的。但有些研究成果表明二者的结果并不完全一致,这可能是以下原因造成的:① 若增广系数矩阵各元素服从独立等精度分布,则简单TLS估计和LS估计结果应一致,但实际应用中由于矩阵元素有很多常数,导致每个元素并非服从独立等精度分布,从而引起差异;② 假设元素之间按行或按列独立,残差等精度等,而未考虑元素之间准确的相关关系;③ 未进行迭代计算;④ 单位权中误差的计算方法不一致。
6 结 论(1) 对于EIV问题,加权总体最小二乘与经典附参数的条件平差问题估计结果一致,二者是同一测量平差问题的两种不同解法。
(2) 在进行加权总体最小二乘时,关键在权阵的选取,必须分清观测值、参数、系数矩阵元素、残差之间的误差传播关系,特别是矩阵元素的方差,否则将会导致总体最小二乘方法与经典平差结果不一致。
(3) 由于RWTLS估计方法中,残差与参数初值有关,因此需要迭代计算,而且需要注意参数初值可能导致的迭代发散问题。
(4) 两种估计方法虽然在理论上是一致的,但计算的复杂程度不相同,建议根据不同的函数模型选用平差方法。对于经典大地测量问题,由于线性化后系数矩阵元素的误差关系复杂,建议选用原有经典平差方法。而对于数字摄影测量、三维激光扫描数据等中的数据拟合、坐标变换、核线估计等问题,系数矩阵大多只包含观测值且按行分块独立,则选用RWTLS方法更为方便。
| [1] | YU Zongcou, YU Zhenglin. Principle of Surveying Adjustment[M]. Wuhan:Publishing House of Wuhan Technology University of Surveying and Mapping,1990.(於宗俦,于正林.测量平差原理[M].武汉:武汉测绘科技大学出版社,1990.) |
| [2] | ZHU Jianjun, SONG Yingchun. Progress of Modern Surveying Adjustment and Theory of Data Processing[J]. Geotechnical Investigation and Surveying, 2009,37(12):1-5.(朱建军,宋迎春.现代测量平差与数据处理理论的进展[J].工程勘察,2009,37(12):1-5.) |
| [3] | OU Jikun. Uniform Expression of Solutions of Ill-posed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights[J]. Acta Geodaetica et Cartographica Sinica, 2004,33(4):283-288.(欧吉坤.测量平差中不适定问题解的统一表达与选权拟合法[J].测绘学报,2004,33 (4):283-288.) |
| [4] | OUYANG Wensen, ZHU Jianjun . Expanding of Classical Surveying Adjustment Model[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(1):12-15.(欧阳文森,朱建军.经典平差模型的扩展[J].测绘学报,2009,38(1):12-15.) |
| [5] | FENG Guangcai, ZHU Jianjun, CHEN Zhengyang,et al. A New Approach to Inequality Constrained Least-squares Adjustment [J]. Acta Geodaetica et Cartographica Sinica, 2007,36 (2):120-123.(冯光财,朱建军,陈正阳,等.基于有效约束的附不等式约束平差的一种新法[J].测绘学报,2007,36 (2):120-123.) |
| [6] | PENG Junhuan, ZHANG Yali, ZHANG Hongping ,et al. The Solution of Inequality-contrained Least Squares Problem and Its Statistical Properties[J]. Acta Geodaetica et Cartographica Sinica , 2007,36 (1) :50-55. (彭军还,张亚利,章红平,等.不等式约束最小二乘问题的解及其统计性质[J].测绘学报,2007,36 (1):50-55.) |
| [7] | LU Tieding,TAO Benzao,ZHOU Shijian. Modeling and Algorithm of Linear Regression Based on Total Least Squares[J].Geomatics and Information Science of Wuhan University, 2008,33(5):504-507.(鲁铁定,陶本藻,周世健.基于整体最小二乘法的线性回归建模和解法[J].武汉大学学报:信息科学版,2008,33(5):504-507.) |
| [8] | LU Jue, CHEN Yi, ZHENG Bo.Applying Total Least Squares to Three Dimensional Datum Transformation[J].Journal of Geodesy and Geodynamics,2008,28(5):77-81.(陆珏,陈义,郑波.总体最小二乘方法在三维坐标转换中的应用[J].大地测量与地球动力学,2008,28(5):77-81.) |
| [9] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J].Journal of Geodesy,2008, 82(7):415-421. |
| [10] | SCHAFFRIN B, FELUS Y A. On the Multivariate Total Least-squares Approach to Empirical Coordinate Transformations——Three Algorithms[J]. Journal of Geodesy,2008, 82(6):373-383. |
| [11] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis ,1980, 17:883-893. |
| [12] | VAN HUFFEL S, VANDEWALLE J. The Total Least Squares Problem[M]. Philadelphia:SIAM,1991. |
| [13] | MARKOVSKY I, VAN HUFFEL S.Overview of Total Least Squares Methods[J].Signal Process,2007,87: 2283-2302. |
| [14] | MARKOVSKY I, RASTELLO M, PREMOLI P, et al. Element-wise Weighted Total Least Squares Problem[J]. Computational Statistics and Data Analysis,2006,50:181-209. |
| [15] | MVHLICH M, MESTER R. Subspace Methods and Equilibration in Computer Vision[C]//Proceedings of 12th Scandinavian Conference on Image Analysis. Stavanger:[s.n.], 2001: 415-422. |
| [16] | SCHAFFRIN B,FELUS Y A. On Total Least-squares Adjustment with Constraints[C]//Proceedings of Windows on the Future of Geodesy. Berlin:IAG-Symp, 2005: 417-421. |