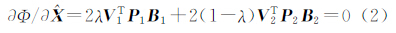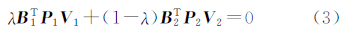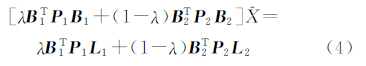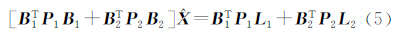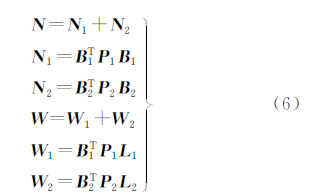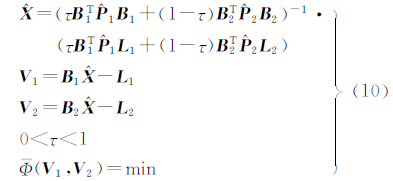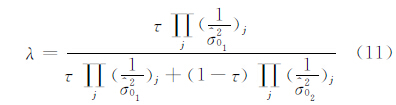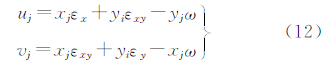2. 武汉大学 测绘学院, 湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
1 引 言
大地测量地球物理联合反演可以融合多种数据(大地测量数据、地震波数据、地质数据以及地球物理数据等),研究地球动力学,反演活动断层、块体的运动情况,探讨地壳运动与地震的关系,是大地测量学深入地学研究领域的一个重要的手段。联合反演应用的一个关键问题是相对权比的确定,它体现了各类资料在联合反演中贡献的大小,一个成功的联合反演必须有一个合理的相对权比,因此相对权比的研究是当今联合反演研究的一个热点问题,得到了广泛关注[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]。目前相对权比确定的方法主要有4种:将相对权比当做未知数与模型参数一同反演求解;根据先验信息(验前方差)确定相对权比;相对权比人为定为0.5;赫尔墨特方差分量估计法[2, 3, 4, 7, 9, 13]。本文针对这些方法的优缺点,提出确定线性联合反演中相对权比的两步法,最后通过模拟计算显示方法的有效性和可行性。
2 确定联合反演中相对权比的两步法对于线性反演模型,假设有两种不同类型的观测数据,联合反演的目标函数为
式中,V1=B1 -L1;V2=B2
-L1;V2=B2 -L2;λ(0<λ<1)为相对权比(由于是联合反演,因此本文λ不取0和1);P1=Q1-1;P2=Q2-1为权阵。
-L2;λ(0<λ<1)为相对权比(由于是联合反演,因此本文λ不取0和1);P1=Q1-1;P2=Q2-1为权阵。
将式(1)对 求导有
求导有
转置后得
将V1和V2代入上式,整理得
两步法确定线性联合反演模型中相对权比的具体步骤如下。
(1) 第1步,用方差分量估计得到两类数据的权阵的估值为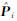 (i=1,2),以及单位权方差的估值
(i=1,2),以及单位权方差的估值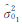 和
和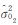 。具体步骤为:
。具体步骤为:
① 先不考虑相对权比λ,联合反演的目标函数为
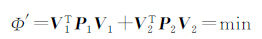
确定两类观测资料权的初值P1和P2,选取时根据前面计算得到的结果作为初值,如利用GPS和地震矩张量联合反演地壳运动速度场时,P1可选为GPS站速度场的先验权阵,P2可选为平均应变率的先验权阵。一般来说两类观测数据的权P1和P2是可能不准确的,也就是说P1和P2所对应的单位权方差不相等(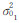 ≠
≠ )。联合反演中利用赫尔墨特方差分量估计的前提是:两类或多类观测值之间是相互独立的,不独立时必须利用方差-协方差分量估计来确定单位权方差与单位权协方差,然后获得合理的观测值权阵。
)。联合反演中利用赫尔墨特方差分量估计的前提是:两类或多类观测值之间是相互独立的,不独立时必须利用方差-协方差分量估计来确定单位权方差与单位权协方差,然后获得合理的观测值权阵。
② 进行第一次求解, =[N1+N2]-1[W1+W2],V1=B1
=[N1+N2]-1[W1+W2],V1=B1 -L1,V2=B2
-L1,V2=B2 -L2,求得V1TP1V1和V2TP2V2。
-L2,求得V1TP1V1和V2TP2V2。
③ 进行第一次方差分量估计[15]
式中
求得两类观测数据单位权方差的第1次估值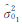 和
和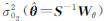 ,再用下式定权[15]
,再用下式定权[15]
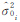 中的某一个值。
中的某一个值。
④ 反复进行步骤②和步骤③,即进行求解ViTPiVi(i=1,2)—方差分量估计(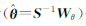 —定权后
—定权后 (i=1,2)再求解ViTPiVi(i=1,2),直至
(i=1,2)再求解ViTPiVi(i=1,2),直至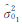 =
=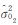 为止,或通过必要的检验认为两类单位权方差之比等于1为止。
为止,或通过必要的检验认为两类单位权方差之比等于1为止。
第1步所用的方程为

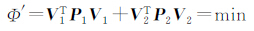
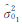 =
=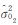 。
。
(2) 第2步,根据第1步得到的两类观测资料权阵的估值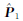 和
和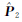 ,在式(10)下求取相对权比和模型参数,即
,在式(10)下求取相对权比和模型参数,即
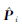 (i=1,2)的相对权比,与式(1)中对应于Pi(i=1,2)的相对权比λ不同;Φ(V1,V2)是V1和V2的函数,常用Φ(V1,V2)函数主要有
(i=1,2)的相对权比,与式(1)中对应于Pi(i=1,2)的相对权比λ不同;Φ(V1,V2)是V1和V2的函数,常用Φ(V1,V2)函数主要有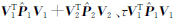 +
+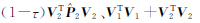 和∑|V1|+∑|V2|等。本文算例部分将进行详细讨论。
和∑|V1|+∑|V2|等。本文算例部分将进行详细讨论。
具体步骤是:选定一个步长,让权比例因子τ遍历整个取值区间0<τ<1,每个τ对应于一个参数解 和Φ(V1,V2),把其中Φ(V1,V2)的最小值对应的参数向量和此时的权比例因子作为最终结果。
和Φ(V1,V2),把其中Φ(V1,V2)的最小值对应的参数向量和此时的权比例因子作为最终结果。
由式(9)和式(10)得λ与τ的关系为
式中,j=1,2,3,…为两步法第1步的迭代次数。可以将两步法简单概括如下:第1步是不考虑相对权比,建立两类或多类数据的联合反演模型,通过赫尔墨特方差分量估计使得两类或多类观测数据的单位权方差相等(或单位权方差的比值接近1),从理论上确定观测数据合理的权阵,同时对不同种类数据进行归一化;第2步是在获得合理的观测数据权阵之后,建立顾及相对权比的联合反演模型,将相对权比和模型参数当做未知数同时进行反演,以目标函数值为最小来确定权比例因子。两步法是一种概括反演方法,赫尔墨特方差分量估计法、将相对权比当做未知数同模型参数一同反演的方法以及单一反演方法都是两步法的特例;其优点是可以获得观测数据合理权阵,同时使得顾及相对权比的联合反演目标函数取得最小值,并对各类观测数据进行归一化。
当不同源数据出现量纲不一致情况时,首先需要对多源数据进行无量纲化处理,常用的方法为[fiobs-Fi(m)]/fiobs或[fiobs-Fi(m)]/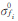 ,其中fiobs为观测数据,Fi(m)为各自模型拟合的观测值,
,其中fiobs为观测数据,Fi(m)为各自模型拟合的观测值,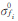 为观测数据的标准差,下标i表示第i类数据[10]。
为观测数据的标准差,下标i表示第i类数据[10]。
在假定介质均匀且邻近测点间应变均匀的情况下,可以建立邻近点间相对形变量与地壳应变张量的线性关系[16]。设监测网第j点两期纵坐标位移为uj,横坐标位移为vj,网中共有m点,则由坐标位移反演应变参数的公式(二维)为[17]
式中,xj、yj(j=1,2,…,m)为第j点近似坐标;ω为其转动量;εx、εy、γxy为应变状态参数,且γxy=2εxy。利用该应变参数反演模型模拟生成了反演应变参数的GPS坐标位移数据和边角网平差后的坐标位移数据(u1、v1)和(u2、v2),并对两类观测资料分别施加了σ2=0.5 mm2和σ2=1.0 mm2的随机噪声后的数据为(u′1、v′1)和(u′2、v′2)。具体见表 1和表 2,相应的坐标位移协因数阵数据分别见表 3和表 4。
| 序号 | X/m | Y/m | u1/mm | v1/mm | u′1/mm | v′1/mm |
| 1 | 100.000 | 100.000 | 1.000 | 20.200 | 0.783 7 | 19.367 2 |
| 2 | 100.000 | 300.000 | -1.000 | 18.600 | -0.937 3 | 18.743 8 |
| 3 | 100.000 | 500.000 | -3.000 | 17.000 | -3.573 2 | 17.595 5 |
| 4 | 300.000 | 100.000 | 5.000 | 62.200 | 5.594 6 | 62.181 2 |
| 5 | 300.000 | 300.000 | 3.000 | 60.600 | 3.163 6 | 60.687 3 |
| 6 | 300.000 | 500.000 | 1.000 | 59.000 | 0.906 6 | 59.362 9 |
| 7 | 500.000 | 100.000 | 9.000 | 104.200 | 8.705 8 | 105.291 6 |
| 8 | 500.000 | 300.000 | 7.000 | 102.600 | 6.931 8 | 102.657 0 |
| 9 | 500.000 | 500.000 | 5.000 | 101.000 | 5.533 4 | 101.029 6 |
| 序号 | X/m | Y/m | u2/mm | v2/mm | u′2/mm | v′2/mm |
| 1 | 100.000 | 100.000 | 1.000 | 20.200 | 0.567 4 | 18.534 4 |
| 2 | 100.000 | 600.000 | -4.000 | 16.200 | -3.874 7 | 16.487 7 |
| 3 | 600.000 | 100.000 | 11.000 | 125.200 | 9.853 5 | 126.390 9 |
| 4 | 600.000 | 600.000 | 6.000 | 121.200 | 7.189 2 | 121.162 4 |
| u1 | v1 | u2 | v2 | u3 | v3 | u4 | v4 | u5 | v5 | u6 | v6 | u7 | v7 | u8 | v8 | u9 | v9 | |
| u1 | 9.2 | 2.1 | -1.6 | 2.8 | -1.9 | 3.2 | 3.7 | -2.6 | 3.1 | 4.7 | 6.3 | 4.1 | -1.6 | 5.4 | 2.9 | -1.1 | 2.9 | -1.8 |
| v1 | 2.1 | 8.6 | 4.7 | -1.9 | 4.2 | 3.5 | 7.8 | -1.1 | -2.7 | 5.3 | 4.8 | -1.2 | 5.7 | 3.9 | 3.7 | 4.6 | 3.4 | 5.1 |
| u2 | -1.6 | 4.7 | 10.7 | 5.8 | 3.9 | 4.1 | 6.2 | 4.3 | -1.4 | 3.8 | 1.9 | 3.9 | 2.8 | 4.2 | -1.5 | 6.3 | -1.1 | 3.6 |
| v2 | 2.8 | -1.9 | 5.8 | 9.8 | 3.3 | -1.8 | 4.1 | 5.2 | 2.2 | 2.9 | 4.6 | -1.5 | 3.9 | 2.6 | 4.3 | 6.6 | -1.4 | 3.9 |
| u3 | -1.9 | 4.2 | 3.9 | 3.3 | 11.4 | 3.5 | -2.8 | 3.0 | 2.7 | 4.3 | 6.0 | 4.3 | -1.1 | 2.7 | -1.7 | 3.3 | 2.7 | 4.0 |
| v3 | 8.2 | 3.5 | 4.1 | -1.8 | 3.5 | 10.7 | 4.2 | -1.3 | 5.1 | 2.7 | 6.2 | -1.3 | -1.5 | 3.7 | 4.1 | 6.3 | -1.3 | 4.5 |
| u4 | 3.7 | 7.8 | 6.2 | 4.1 | -2.8 | 4.2 | 9.9 | -1.8 | -1.2 | 4.6 | 3.9 | 5.1 | -2.7 | 7.1 | 4.6 | 2.9 | 4.2 | 3.4 |
| v4 | -2.6 | -1.1 | 4.3 | 5.2 | 3.0 | -1.3 | -1.8 | 8.3 | 3.8 | 2.7 | 4.8 | -1.7 | -1.3 | 3.8 | -1.5 | 3.4 | 2.7 | -1.9 |
| u5 | 3.1 | -2.7 | -1.4 | 2.2 | 2.7 | 5.1 | -1.2 | 3.8 | 10.6 | 3.2 | -1.1 | -1.3 | -1.9 | 4.7 | 5.9 | 2.8 | 4.6 | -1.1 |
| v5 | 4.7 | 5.3 | 3.8 | 2.9 | 4.3 | 2.7 | 4.6 | 2.7 | 3.2 | 9.9 | 1.6 | 2.3 | -1.0 | 2.4 | 2.7 | -1.1 | 2.0 | 1.6 |
| u6 | 6.3 | 4.8 | 1.9 | 4.6 | 6.0 | 6.2 | 3.9 | 4.8 | -1.1 | 1.6 | 8.2 | -2.7 | -1.1 | 2.7 | 1.8 | 3.0 | -1.1 | 3.7 |
| v6 | 4.1 | -1.2 | 3.9 | -1.5 | 4.3 | -1.3 | 5.1 | -1.7 | -1.3 | 2.3 | -2.7 | 10.4 | 1.9 | -1.4 | 5.0 | 4.3 | 3.7 | 2.9 |
| u7 | -1.6 | 5.7 | 2.8 | 3.9 | -1.1 | -1.5 | -2.7 | -1.3 | -1.9 | -1.0 | -1.1 | 1.9 | 9.6 | -2.3 | 3.0 | 2.9 | 4.1 | -1.7 |
| v7 | 5.4 | 3.9 | 4.2 | 2.6 | 2.7 | 3.7 | 7.1 | 3.8 | 4.7 | 2.4 | 2.7 | -1.4 | -2.3 | 8.8 | -1.7 | 4.6 | -2.7 | 3.6 |
| u8 | 2.9 | 3.7 | -1.5 | 4.3 | -1.7 | 4.1 | 4.6 | -1.5 | 5.9 | 2.7 | 1.8 | 5.0 | 3.0 | -1.7 | 8.4 | -1.1 | 2.7 | 3.7 |
| v8 | -1.1 | 4.6 | 6.3 | 6.6 | 3.3 | 6.3 | 2.9 | 3.4 | 2.8 | -1.1 | 3.0 | 4.3 | 2.9 | 4.6 | -1.1 | 9.6 | -1.1 | 2.9 |
| u9 | 2.9 | 3.4 | -1.1 | -1.4 | 2.7 | -1.3 | 4.2 | 2.7 | 4.6 | 2.0 | -1.1 | 3.7 | 4.1 | -2.7 | 2.7 | -1.1 | 10.2 | -1.5 |
| v9 | -2.8 | 5.1 | 3.6 | 3.9 | 4.0 | 4.5 | 3.4 | -1.9 | -1.1 | 1.6 | 3.7 | 2.9 | -1.7 | 3.6 | 3.7 | 2.9 | -1.5 | 8.0 |
| u1 | v1 | u2 | v2 | u3 | v3 | u4 | v4 | |
| u1 | 19.2 | 6.1 | -2.6 | 4.8 | -2.9 | 5.2 | 3.7 | -2.9 |
| v1 | 6.1 | 18.6 | 4.7 | -3.9 | 5.2 | 6.5 | -3.8 | 5.1 |
| u2 | -2.6 | 4.7 | 16.7 | 5.8 | -3.9 | 4.1 | 6.2 | -4.3 |
| v2 | 4.8 | -3.9 | 5.8 | 15.8 | 6.3 | -3.8 | 4.4 | 5.2 |
| u3 | -2.9 | 5.2 | -3.9 | 6.3 | 17.4 | 3.5 | -2.8 | 3.0 |
| v3 | 5.2 | 6.5 | 4.1 | -3.8 | 3.5 | 18.7 | 4.2 | -1.3 |
| u4 | 3.7 | -3.8 | 6.2 | 4.4 | -2.8 | 4.2 | 16.9 | -1.8 |
| v4 | -2.9 | 5.1 | -4.3 | 5.2 | 3.0 | -1.3 | -1.8 | 18.3 |
为了比较本文提出的确定线性联合反演模型相对权比的两步法与其他方法之间的优缺点,利用模拟数据进行了计算,分以下10个方案进行,λ表示GPS坐标位移在联合反演中所占的比重。方案1:GPS坐标位移的单一反演;方案2:边角网平差坐标位移的单一反演;方案3:λ=0.5;方案4:(1-λ)/λ=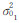 /
/ ,λ=0.666 7;方案5:以Φ= λV1TP1V1 + (1-λ)V2TP2V2 = min,把λ当做未知数同模型参数一同进行反演;方案6:赫尔墨特方差分量估计法[4],迭代终止的条件为两类数据单位权方差估值之差小于等于0.000 1;为了比较两步法中第2步的目标函数Φ(V1,V2)(式(10)所示)的不同对确定相对权比的影响,分别计算了以
,λ=0.666 7;方案5:以Φ= λV1TP1V1 + (1-λ)V2TP2V2 = min,把λ当做未知数同模型参数一同进行反演;方案6:赫尔墨特方差分量估计法[4],迭代终止的条件为两类数据单位权方差估值之差小于等于0.000 1;为了比较两步法中第2步的目标函数Φ(V1,V2)(式(10)所示)的不同对确定相对权比的影响,分别计算了以 、Φ2(V1,V2)=V1TV1+V2TV2=min、Φ3(V1,V2)=τV1T
、Φ2(V1,V2)=V1TV1+V2TV2=min、Φ3(V1,V2)=τV1T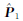 V1+(1-τ)V2T
V1+(1-τ)V2T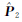 V2=min以及Φ4(V1,V2)=∑|V1|+∑|V2|=min为目标函数确定相对权比的两步法,分别称为方案7、方案8、方案9和方案10,迭代计算时τ步长取为0.000 1;为便于阅读将各方案的所用方法列于表 5中。
V2=min以及Φ4(V1,V2)=∑|V1|+∑|V2|=min为目标函数确定相对权比的两步法,分别称为方案7、方案8、方案9和方案10,迭代计算时τ步长取为0.000 1;为便于阅读将各方案的所用方法列于表 5中。
| 方案 | 方法 |
| 1 | λ=1 |
| 2 | λ=0 |
| 3 | λ=0.5 |
| 4 | (1-λ)/λ=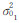 / / ,即λ=0.666 7 ,即λ=0.666 7 |
| 5 | 以Φ=λV1TP1V1 + (1-λ)V2TP2V2=min为目标函数确定相对权比,以式(4)求参数 |
| 6 | 赫尔墨特方差分量估计法 |
| 7 | 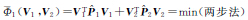 |
| 8 | 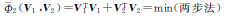 |
| 9 | 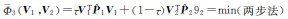 |
| 10 | 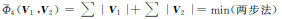 |
各方案应变参数反演结果见表 6。
| εx(×10-6) | εy(×10-6) | εxy(×10-6) | ω(×10-6) | ‖ΔX‖ | λ | |
| R | 20.000 0±0.000 0 | -8.000 0±0.000 0 | 100.000 0±0.000 0 | 110.000 0±0.000 0 | — | — |
| 1 | 20.787 9±0.462 4 | -9.554 0±1.051 4 | 100.768 4±0.518 4 | 111.287 6±0.495 5 | 2.298 7 | 1.000 0 |
| 2 | 19.429 8±1.987 4 | -8.731 8±1.613 5 | 101.002 7±1.158 1 | 108.925 8±1.105 6 | 1.737 8 | 0.000 0 |
| 3 | 19.584 7±0.682 6 | -8.874 4±0.772 5 | 100.962 3±0.453 0 | 109.478 7±0.504 7 | 1.461 1 | 0.500 0 |
| 4 | 19.780 2±0.982 9 | -8.969 2±1.287 5 | 100.916 9±0.712 6 | 109.816 9±0.804 1 | 1.364 5 | 0.666 7 |
| 5 | 20.787 4±1.393 2 | -9.553 5±3.167 0 | 100.768 4±1.561 5 | 111.286 8±1.492 7 | 2.297 7 | 0.999 9 |
| 6 | 20.556 9±0.438 4 | -9.380 0±0.876 6 | 100.779 5±0.439 4 | 110.960 9±0.445 9 | 1.935 3 | 0.955 1 |
| 7 | 20.556 9±0.438 4 | -9.380 0±0.876 6 | 100.779 5±0.439 4 | 110.960 9±0.445 9 | 1.935 3 | 0.955 1 |
| 8 | 20.177 1±0.531 8 | -9.160 7±0.871 8 | 100.834 7±0.453 1 | 110.417 7±0.494 2 | 1.499 9 | 0.851 7 |
| 10 | 20.350 3±0.758 1 | -9.253 7±1.359 8 | 100.805 5±0.694 0 | 110.667 1±0.735 3 | 1.669 9 | 0.904 5 |
由于方案9与方案2等价,因此,表 6中没有列出方案9的计算结果,由方案7、方案8、方案9和方案10的两步法计算出来的相对权比τ分别为0.500 0、0.212 7、0(不加0<τ<1的限制,允许取值0和1)和0.308 2。根据式(11)将对应于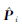 (i=1,2)的相对权比τ转换成对应于式(1)中Pi(i=1,2)的相对权比λ分别为0.955 1、0.851 7、0和0.904 5(如表 6所示);‖ΔX‖表示模型参数反演结果与真值差值的范数;R表示参数的真值。然后,本文绘制了方案5、方案7、方案8、方案9和方案10的目标函数与相对权比之间的关系图,如图 1所示。
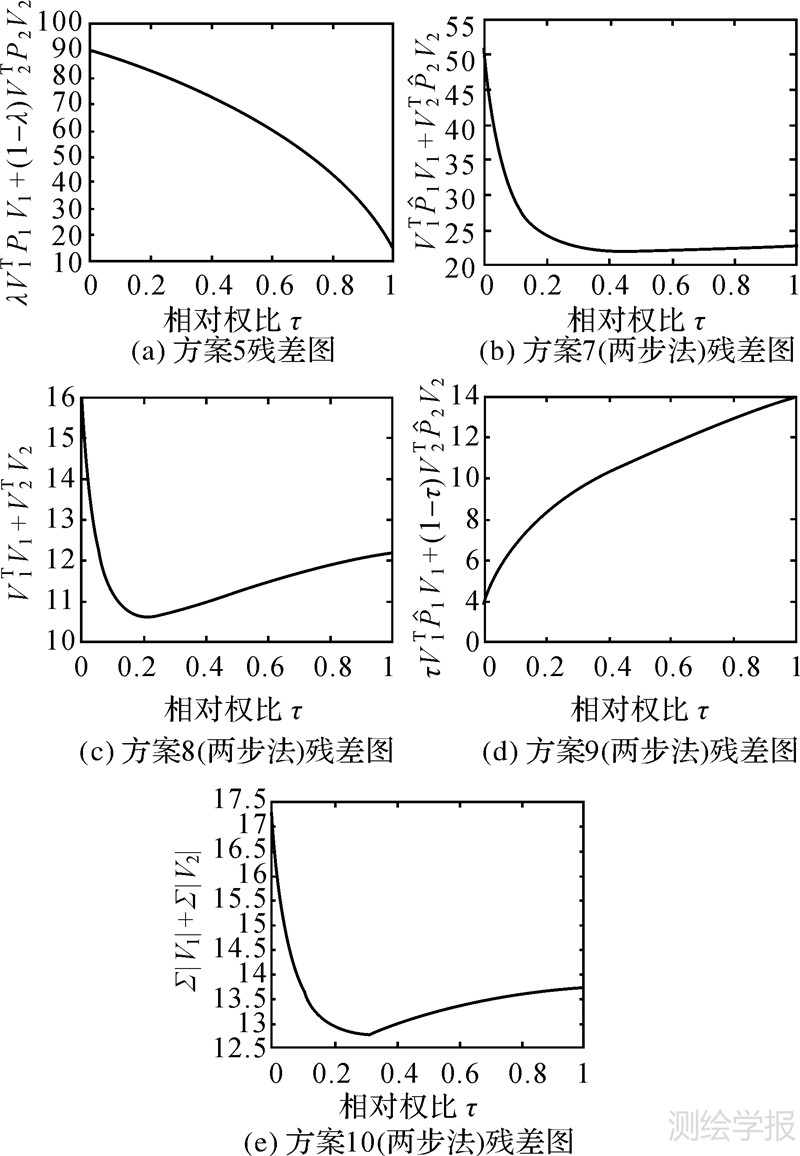
(i=1,2)的相对权比τ转换成对应于式(1)中Pi(i=1,2)的相对权比λ分别为0.955 1、0.851 7、0和0.904 5(如表 6所示);‖ΔX‖表示模型参数反演结果与真值差值的范数;R表示参数的真值。然后,本文绘制了方案5、方案7、方案8、方案9和方案10的目标函数与相对权比之间的关系图,如图 1所示。
|
| 图 1 各方案残差图 Fig. 1 Residual graphs of some projects |
(1) 对于反演结果的评价一般要从内符合精度和外符合精度两个方面进行综合考虑。本文参数估值的中误差是反演结果的内符合精度指标,反演结果与真值的差值范数‖ΔX‖作为外符合精度指标。整体上从内符合精度来看,方案6和方案7的结果最优,而且二者是等价的。从外符合精度来看,方案4的差值范数最小,这与理论相符,因为给定的权比即为实际权比。然而这种方法不具操作性,因为在反演之前两类数据的验前单位权方差是很难准确知道的;方案3虽然外符合精度较高,但是内符合精度稍差;方案5的结果与方案1几乎相同,若不加0<λ<1的限制允许取值0和1,则方案5与方案1是等价的;方案8具有较高的外符合和内符合精度;方案10具有较高的外符合精度,但内符合精度较差;方案9与方案2等价,为边角网坐标位移的单一反演。综合起来看,当观测值不含粗差时,两步法(除方案10外)可以得到较好的反演结果。
(2) 验前单位权方差法(方案4)的主要缺点是反演结果与给予的验前(初始)单位权方差有着很大的关系。验前单位权方差给的准确,则可以得到较好的结果(如本文的算例),若初始单位权方差不准确,就会得到不好的结果[2, 4]。赫尔墨特方差分量估计法(方案6)的主要优点是得到的结果具有最优无偏的特性,不会受到验前单位权方差不准确的限制。两步法是一种概括反演方法,赫尔墨特方差分量估计法(方案6)以及单一反演方法(方案2)等都是两步法的特例。两步法通过目标函数Φ(V1,V2)的选择统一了这些常用的方法。两步法同样不会受到验前单位权方差不准确的限制,可以获得观测数据合理权阵,同时使得顾及相对权比的联合反演目标函数取得最小值,并对各类观测数据进行了归一化。由图 1可以看出,两步法的第2步采用不同的目标函数确定相对权比的结果是不同的。两步法目标函数Φ(V1,V2)的选取方法为,观测值仅含偶然误差时,若要获得最优无偏的反演结果,则选Φ1(V1,V2)为目标函数;相对权比和模型参数都当做未知数同时计算时,可选Φ2(V1,V2)为目标函数;相对权比和模型参数都当做未知数同时计算时,不可选Φ3(V1,V2)作为目标函数,否则变成单一反演。因此,目标函数的选择可以根据实际情况确定。
(3) 由残差图 1(a)(方案5)和图 1(d)(方案9)可以看出,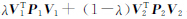 与相对权比λ以及
与相对权比λ以及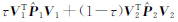 与相对权比τ之间是成递减或递增的关系,因此当以此类目标函数作为确定相对权比的标准,且将其当做未知数与模型参数一同进行求解时,得到相对权比的值为1或者0,如文献[4]中的λ=1。
与相对权比τ之间是成递减或递增的关系,因此当以此类目标函数作为确定相对权比的标准,且将其当做未知数与模型参数一同进行求解时,得到相对权比的值为1或者0,如文献[4]中的λ=1。
(4) 联合反演中相对权比的大小虽然是由所用的方法确定的,但并不能以得到的相对权比的大小作为评价确定相对权比方法好坏的标准。无论采用何种方法确定相对权比,一般精度较高、数目较多的一类观测值应该在联合反演中起主要作用,该观测值的相对权比也较大,如本文算例中的GPS观测数据。
相对权比的确定是联合反演中的关键问题。本文提出的确定联合反演中相对权比的两步法是一种概括反演方法,其优点是不受验前单位权方差的限制,可以获得观测数据的合理权阵,同时使得顾及相对权比的联合反演目标函数取得最小值,并对各类观测数据进行了归一化。模拟数据的计算,显示了在处理线性联合反演问题时该方法是非常有效的。但是,两步法还需要在实际应用中进一步验证和改进。
| [1] | XU Caijun, SHEN Wenbin, CHAO Dingbo. Geophysical Geodesy Principles and Methods[M]. Wuhan: Wuhan University Press, 2006. (许才军,申文斌,晁定波.地球物理大地测量学原理与方法[M].武汉:武汉大学出版社,2006.) |
| [2] | DING Kaihua. Research on Stochastic Modeling in Geodetic Joint Inversion[D]. Wuhan: Wuhan University, 2006. (丁开华.大地测量联合反演中的随机模型研究[D].武汉:武汉大学, 2006.) |
| [3] | FU Yuning. Joint Inversion of Movement Parameters of Main Faults and Blocks in Sichuan and Yunnan Area Using GPS and Gravity Data[D]. Wuhan: Wuhan University, 2007. (富宇宁.利用GPS和重力数据联合反演川滇地区主要断层、块体的运动参数[D].武汉:武汉大学, 2007.) |
| [4] | XU Caijun, DING Kaihua, CAI Jianqing, et al. Methods of Determining Weight Scaling Factors for Geodetic-geophysical Joint Inversion[J]. Journal of Geodynamics, 2009, 47(1): 39-46. |
| [5] | DU Zhixing, OU Jikun, JIN Fengxiang, et al. Optimization Inversion of the Relative Weight Ratio in the Joint Inversion Models[J]. Acta Geodaetica et Cartographica Sinica. 2003, 32(1): 15-19. (独知行,欧吉坤,靳奉祥,等.联合反演模型中相对权比的优化反演[J].测绘学报, 2003, 32(1): 15-19.) |
| [6] | XU Caijun. Progress of Joint Inversion on Geodesy and Geophysics[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6): 555-561. (许才军.大地测量联合反演理论和方法研究进展[J].武汉大学学报:信息科学版, 2001, 26(6): 555-561.) |
| [7] | FU Yuning, XU Caijun. On Relative Weight Problem in Joint Inversion Using Levelling and Gravity Data[J]. Journal of Geodesy and Geodynamics, 2007, 27(2): 68-74. (富宇宁,许才军.水平和重力资料联合反演中权问题的研究[J].大地测量与地球动力学,2007, 27(2): 68-74.) |
| [8] | LI Shuang. Research on Models and Algorithms of Geodesy and Geophysics Joint Inversion[D]. Wuhan: Wuhan University, 2005. (李爽.大地测量联合反演的模式及算法研究[D].武汉:武汉大学,2005.) |
| [9] | DING Kaihua, XU Cajjun. Current Crustal Strain Field in the Sichuan-Yunnan Area by Joint Inversion of GPS and Seismic Moment Tensor[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 265-268. (丁开华,许才军.川滇地区地壳应变场的GPS与地震矩张量联合反演研究[J].武汉大学学报:信息科学版, 2009, 34(3): 265-268.) |
| [10] | ZHAO Shaorong. Joint Inversion of Observed Gravity and GPS Baseline Changes for the Detection of the Active Fault Segment at the Red River Fault Zone[J]. Geophysical Journal International, 1995, 122(1): 70-88. |
| [11] | XU Caijun, WANG Leyang. Progress of Joint Inversion of Geodetic and Seismological Data for Seismic Source Rupture Process[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 457-462. (许才军,王乐洋.大地测量和地震资料联合反演地震震源破裂过程研究进展[J].武汉大学学报:信息科学版,2010, 35(4): 457-462.) |
| [12] | WANG Leyang, XU Caijun. Comparative Research on Equality Constraint Inversion and Joint Inversion[J]. Journal of Geodesy and Geodynamics, 2009, 29(1): 74-78. (王乐洋,许才军.等式约束反演与联合反演的对比研究[J].大地测量与地球动力学, 2009, 29(1): 74-78.) |
| [13] | XU Caijun, LIU Yang, WEN Yangmao, et al. Coseismic Slip Distribution of the 2008 Mw 7.9 Wenchuan Earthquake from Joint Inversion of GPS and InSAR Data[J]. Bulletin of the Seismological Society of America, 2010, 100(5B): 2736-2749. |
| [14] | LIU Chongbing, NING Jinsheng, ZHANG Yushen. Method for Joint Inversion of Seismic Surface Waves and Gravity Data for Three Dimensional Density Structure[J]. Acta Geodaetica et Cartographica Sinica. 1999, 28(2): 103-109. (刘崇兵,宁津生,张禹慎.利用地震面波和重力资料联合反演地壳-上地幔三维密度结构的方法探讨[J].测绘学报, 1999, 28(2): 103-109.) |
| [15] | CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized Surveying Adjustment[M]. New ed. Wuhan:Wuhan Technical University of Surveying and Mapping Press, 2001. (崔希璋,于宗俦,陶本藻,等.广义测量平差[M].新版.武汉:武汉测绘科技大学出版社, 2001.) |
| [16] | TAO Benzao. Robust Homogeneous Analysis of Displacement-Strain Models[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(4): 293-296. (陶本藻.位移-应变模型的稳健均匀分析[J].测绘学报, 2000, 29(4): 293-296.) |
| [17] | CHEN Jian, TAO Benzao. Geodetic Deformation Surveying[M]. Beijing: Earthquake Publishing House, 1987. (陈健,陶本藻.大地形变测量学[M].北京:地震出版社, 1987.) |