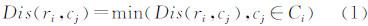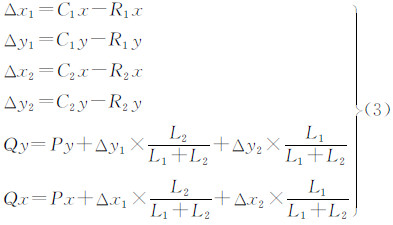2. 华中师范大学 城市与环境科学学院,湖北 武汉 430079
2. College of Urban and Environment Science, Central China Normal University, Wuhan 430079, China
1 引 言
空间数据库建立及更新需集成多种来源数据,存在匹配中的不一致问题。这种不一致可能发生在不同主题、不同比例尺、不同时态的数据集成中,其表现形式包括要素表达不一致、邻近关系冲突、拓扑结构不一致、地理匹配关系矛盾等。而一致性作为空间数据质量的5大特征之一[1],是空间分析、空间决策、空间数据挖掘等过程中应考虑的重要因素,因此,如何将异源数据进行有效地匹配,并探测、纠正不一致成为当前GIS领域的热点。
当前,相关研究多集中于同类要素对象间的匹配及一致性维护(如道路网[2, 3]、河流[4]、居民地[5, 6]等),通过几何特征、属性特征及拓扑关系的相似性比较建立匹配关系[2, 3, 4, 5, 6, 7, 8, 9, 10, 11],利用Delaunay三角网[12]、共轭点控制变换[6]等几何方法实现一致性改正,而不同类要素对象间的匹配及一致性关系的维护由于缺少匹配条件而较少涉及。地理学第一定律[13]认为地表所有事物和现象在空间上都是关联的,距离越近,关联程度越强,距离越远,关联程度越弱。这种关联关系表现为空间实体目标相互作用、相互影响形成特定结构的分布模式与依存关系,如某区域特定海拔高度与对应分布的植被类型具有一定的约束。这种发生在不同地理要素间的关联关系对地理特征认知、空间建模、空间推理等有重要意义,也可以作为空间数据匹配的理论依据。
以地形图上的水网、等高线为例,河流与地表地形间相互制约、相互作用,河流通过流水侵蚀、泥沙淤积一刻也不停地改变着地貌形态,导致水网与等高线的分布形成了特定的模式,在地形图表达上水网与等高线隐含谷底线所在位置应该一致。这种分布模式细化到几何关系上包括:① 谷底点应与水网和等高线的交点重合;② 谷底线与水网重叠;③ 水网流向与谷底线沿高程降低的延伸方向一致。这些约束关系可以作为两种数据匹配及是否一致的考察依据。
水网与等高线数据集成、更新过程中,由于数据的采集方式、更新周期及制图过程中抽象概括程度不同,往往产生违背上述约束的情况,导致水网“爬坡”、等高线“入水”现象。当前,对这种空间关系冲突的检测及纠正主要依靠作业员手工操作,效率低且易错判、漏判,急需一种自动检测及维护方法。基于上述分析,解决问题的关键在于如何利用水网与等高线间的约束条件建立正确的匹配关系,并提出一致与否的评判规则。文献[14]通过矢量投影法寻找等高线与水网对应的谷底点,比较谷底点至水网最小垂距检测两者是否一致,这种方法适用的前提是水网与对应谷底线相距较近且近似平行,实际应用有一定局限性,对于不一致的改正方法没有作进一步探究。
本研究以水网、等高线线匹配为例探讨这种不同类要素间的匹配问题,对它们之间的不一致进行探测并提出改正方法,基本思想是在等高线上利用Delaunay三角网提取谷底特征点,与水网和等高线交点建立匹配关系,当水网与谷底线在距离、方向上相差较大时,认为两者不一致。采用两种策略进行一致化改正,一是将水网移位至谷底线处,二是局部移位等高线,使隐含的谷底线与水网一致。方法选择取决于两种数据的定位精度及数据的具体应用背景。
2 Delaunay三角网模型支持下谷底特征提取等高线是通过等高度曲线的投影来表达三维地形,地形特征(如峰、洼地、山脊、谷地等)隐含在等高线表达中。判断等高线与水网匹配是否一致,其实质是判断谷底线与水网是否一致,为建立两者间的匹配关系,首先要从等高线提取谷底特征。
从等高线提取地形结构特征有两种途径:一是将矢量等高线转化为栅格DEM数据,应用图像处理方法根据极值点跟踪或最陡坡降原则提取地形结构特征[15, 16];二是单根等高线上的弯曲可看做谷地或山脊在某一高度水平面上的投影片段,谷地、山脊在等高线模型上表现为相应弯曲的集合,因此,通过对等高线弯曲特征分析可以直接提取地形结构特征[17, 18]。相比第1种方法,通过弯曲特征分析直接提取地形结构特征可以有效避免DEM方法中的噪音干扰,并且结合弯曲特征的层次关系和分布形态可增强谷地树组织的结构化特征。
这里采用文献[17]中的方法从等高线提取谷底点并建立谷底线网络结构。对单根等高线上的平面点集建立Delaunay三角网,选取位于谷地所在单侧的三角形子集,根据三角形间的邻近关系搜索建立弯曲段之间层次包含关系的二叉树[19],然后基于一定的分辨率提取合适的等高线弯曲作为“谷地片段”,其中分辨率控制条件为谷地深度(在弯曲特征上表现为三角网骨架线距离)。在选取的“谷地片段”弯曲中,考察其包含的三角形,提取骨架线建立以弯曲开口中点为根节点的骨架树,比较根节点到叶节点的路径距离,其中距离最长的叶节点即谷底点。如图 1所示,O点为弯曲开口连线中点,比较O到叶节点A、B、C、D的距离,确定距离最远处的C为该弯曲的谷底点。等高线组提取“谷地片段”后,根据水流方向、坡降方向纵向连接谷底点便可得到谷底线,如图 2中的点群是“谷地片段”对应的谷底点,在连接为谷底线的过程中需考虑最短距离、法线方向、相交性等几何约束条件。

|
| 图 1 骨架线最长分支确定谷底特征点C Fig. 1 The end point C is regarded as the valley bottom point according to the longest skeleton branch principle |

|
| 图 2 等高线组上谷底点提取 Fig. 2 The extraction of terrain valley points from contour group |
等高线隐含谷底线与等高线正向相交,同时水网也与等高线相交,可通过比较同一等高线上谷底点与水网和等高线交点的位置关系进行两者间的匹配,对应图 3算法叙述如下:
(1) 建立水网和等高线交点集合R{r1,r2,…,rn}。
(2) 任一ri∈R,搜索其两侧分布的谷底点建立匹配候选集Ci{c1,c2,…,cn},比较ri与Ci中各谷底点间等高线线段长度,按照距离最近原则(式(1)),得到与ri匹配谷底点cj(简称“匹配对m(ri,cj)”)
(3) 循环执行步骤(2),建立水网和等高线交点与谷底点间的匹配对集合M{m1,m2,…,mn}。

|
| 图 3 建立匹配关系 Fig. 3 Building the matching relation |
步骤(2)中谷底点匹配候选集Ci的大小由单侧搜索候选谷底点个数控制。图 3中ri对应谷底点匹配候选集为{C1,C2,C3,C4},按距离最近原则匹配的谷底点为C2,图 4中的虚线连接为谷底点与水网和等高线交点的匹配对应关系。

|
| 图 4 谷底点与水网和等高线交点匹配关系 Fig. 4 The matching relation between terrain valley points and intersection points of river network and contour |
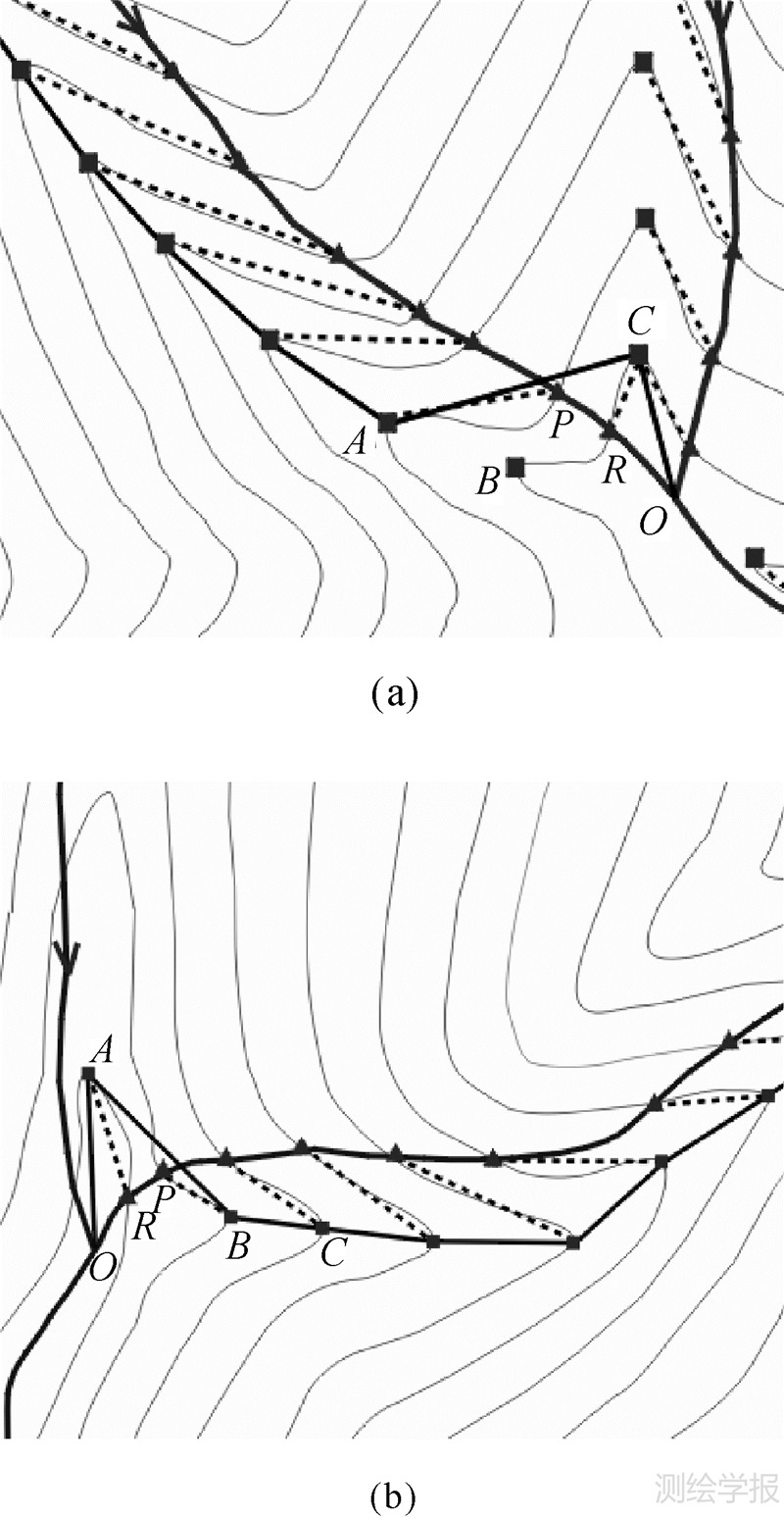
上述匹配过程仅考虑了单个水网和等高线交点与谷底点间的位置关系,未顾及水网流向及整体匹配情况,可能产生错误的匹配关系,需进行正确性检查及改正。图 5(a)中水网和等高线交点R面临谷底点B、C待匹配,按照距离最近原则,匹配结果为(R,C),而正确匹配应为(R,B),图 5(b)中R点实际经过的区域等高线没有明显的弯曲存在(这种情形在河流的下游或主支流汇合时经常出现),不存在与R点匹配的谷底点。类似上述错误匹配,根据谷底线方向(指谷底线沿高程降低的方向)与水网流向的一致性进行补救,算法如下:
(1) 按水网流向排序匹配对集M{m1,m2,…,mn},连接水网和等高线交点及谷底点近似表示水网及谷底线,谷底线两端点与邻近水网节点相连。
(2) 对mi(ri,ci),分别计算ri、ci相邻有向线段间顺时针方向夹角ai、bi,夹角差值θi=|ai-bi|。
(3) 取夹角差值最大θp的匹配对mp(rp,cp),若θp>Δθ,从rp对应的谷底点匹配候选集Cp中剔除cp,然后选取新的匹配谷底点更新匹配对mp(若Cp为空,不存在与rp匹配的谷底点,删除匹配对mp),执行步骤(2);若θp<Δθ,检查结束。
(4) 得到补救后的匹配对集M{m1,m2,…,mk}。
|
| 图 5 错误的匹配关系 Fig. 5 The wrong matching relation |
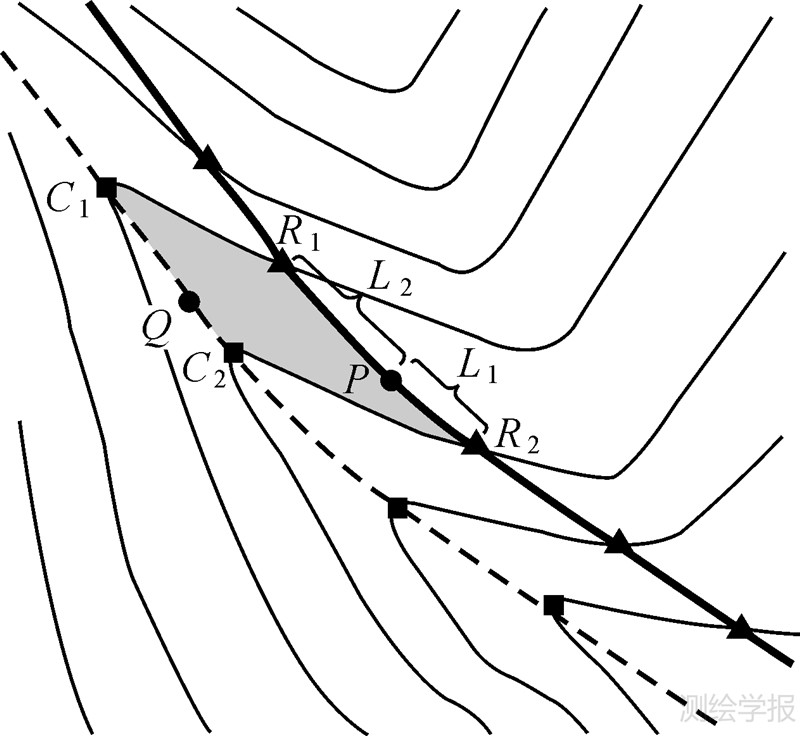
评价水网和等高线是否一致,可以采用水网和谷底线间的距离关系作为依据。如图 6所示,(R1,C1)和(R2,C2)为相邻匹配对,线段C1C2近似表示谷底线,通过下式
求得水网线段R1R2与C1C2间平均距离表示两者间的距离关系。式(2)中S为R1R2、C1C2与等高线围成的多边形(图中阴影部分)面积,L1、L2分别表示R1R2与C1C2的长度。定义水网和等高线一致性改正的位置精度约束值(以水网和谷底线间距离的大小表示),当水网和谷底线间平均距离大于0且小于该约束值,认为水网与等高线不一致,并可进行一致性改正。当两者间平均距离大于该约束值,则产生的不一致性不能简单通过移动某目标的位置来改正,否则位置精度损失导致新的数据质量问题。一致性改正约束值设置需要考虑具体应用背景,如GB/T18315—2001规定1∶50 000地形图山地区域地物点对最近野外控制点的图上点位中误差不能超过0.75 mm,最大误差为中误差的2倍,一致性改正约束值可取实地37.5~75 m之间。
|
| 图 6 水网移位匹配等高线 Fig. 6 The displacement of river network to match contour |
一致性检查后,对不一致的水网和等高线进行改正的方式包括移动水网匹配等高线和移动等高线匹配水网,可以将两种数据的定位精度作为选择标准。当等高线定位精度高时,进行水网移位匹配等高线;反之,等高线移位匹配水网;当两种数据定位精度未知时,一致性改正可能造成定位精度的损失,此时一致性和定位精度成为了矛盾的两个方面,需要结合数据的应用要求进行决策,若定位精度更为重要则不宜进行一致性改正。
4.1 水网移位匹配等高线简单的改正方法便是由相邻等高线间的谷底点顺次相连代替原来水网局部线段,但是当等高距较大时,不能很好地表现出水网的弯曲走势,以谷底点与水网和等高线交点的匹配关系作为控制条件,通过线性变换移位原始水网可以较好地解决这个问题。图 6中水网线段R1R2,以端点R1、R2为控制点分别移位至C1、C2,其余点根据与两端点间的线段长度作相应移位,如P点与R1、R2间线段长度以L1、L2表示,移位后对应点Q通过式(3)求得。该方法在移位水网使之与等高线一致化的同时,较好地保持了水网原来的弯曲走势。
当谷底点所在等高线弯曲形态较复杂时,仅以水网线段的两端点作为移位控制点是不够的(如图 7(a)中水网移位后与同一条等高线产生多个交点),需加强移位控制条件。图 7(b)中,提取C1所在弯曲骨架线,取R1R2中点R3,求得骨架线上距R3距离最近点C3,增加控制点R3移位至C3,图 7(c)是增加控制点后水网移位的效果,但是该方法有一定局限性,要求水网线段与相关弯曲骨架线形态结构差别不大。整个水网移位过程中,为保持拓扑连通性,水网节点作为控制点移位前后位置不变。

|
| 图 7 增加移位控制条件避免移位后出现新的不一致情况 Fig. 7 Adding control condition to avoid new inconsis-tency after river network displacement |
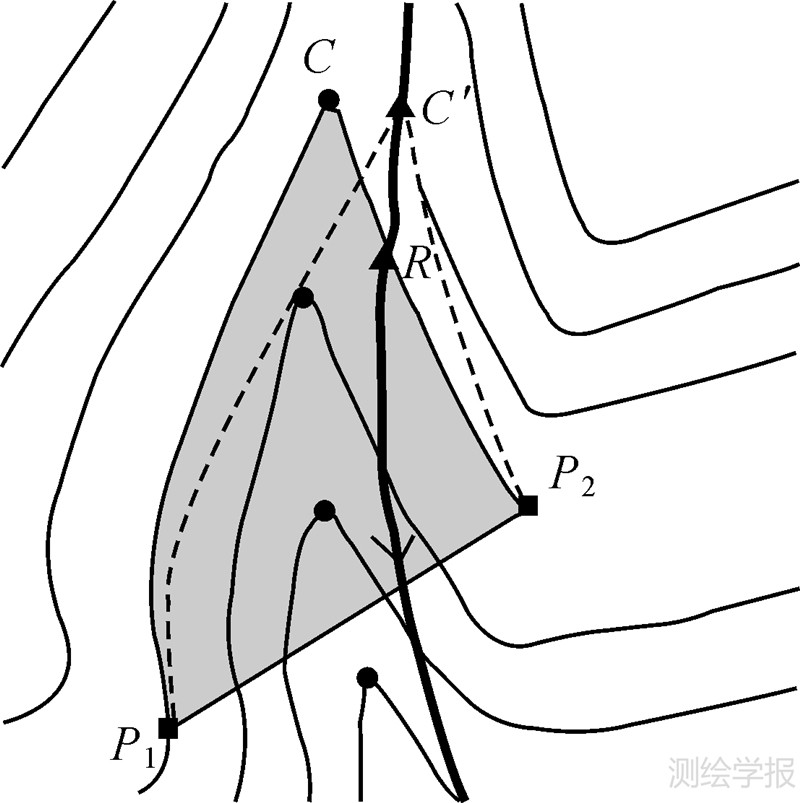
等高线移位的目标是使弯曲隐含的谷底线与水网一致,移位仅针对局部相关等高线的弯曲部分。图 8中C为谷底点,P1、P2为该谷底点所在弯曲的两端点,C′是水网线段上距点C最近的点。以P1、P2、C为弯曲移位控制点,其中P1、P2移位前后位置不变,C移位至C′,弯曲线段上其余点P通过仿射变换(式(4))求得新的坐标位置P′
|
| 图 8 等高线移位匹配水网 Fig. 8 The displacement of contour to match river |
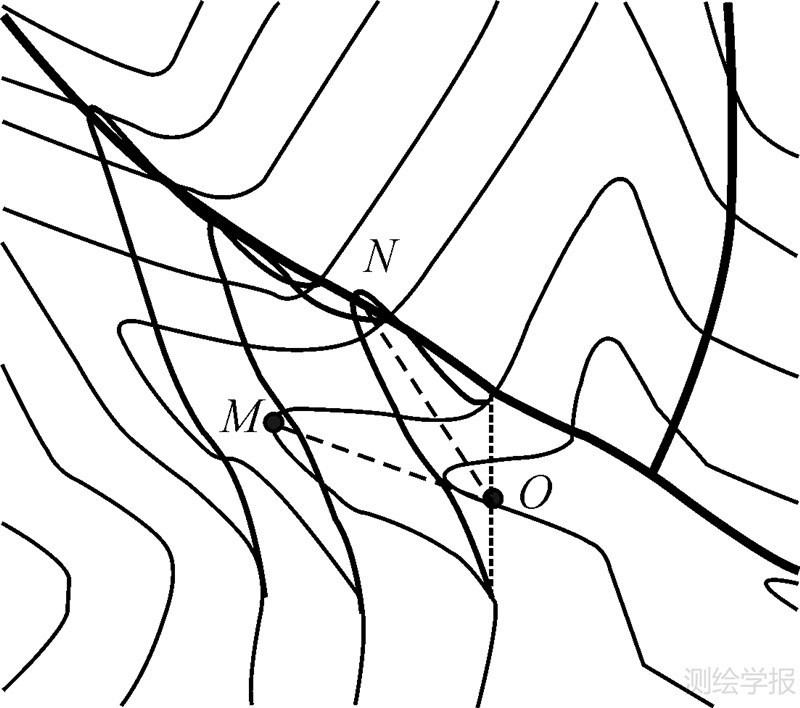
当水网与谷底线相距较远时,等高线弯曲部分移位后形态变化较大,可能出现相邻等高线相交及同一等高线与水网存在多个交点。如图 9,整个谷底点M所在等高线弯曲位于水网一侧,移位后弯曲开后方向发生较大变化,出现了明显的数据不一致,这种情况仅通过移位单个弯曲部分无法达到一致化的效果,需局部扩大移位的等高线范围。与水网移位相比,等高线由于成组分布且形状变化较大,移位后产生新的数据冲突较多,需要探索更好的移位方法。
|
| 图 9 等高线移位后出现相交 Fig. 9 Contours intersected after displacement |
试验数据为云南省谷地特征较为明显的山地区域地形图数据,该数据为在1∶1万地形图基础上通过综合缩编后得到的1∶5万地形图数据,等高距40 m,现要求对综合结果数据的水网和等高线作一致性检测维护。
匹配一致化过程涉及参数的取值需考虑具体区域特点及数据质量的要求。试验数据中“谷地片段”弯曲深度大致在104~445 m之间,取深度阈值465 m以保证识别所有“谷地片段”弯曲。设置水网和等高线交点单侧搜索匹配候选谷底点4个,超过该范围的谷底点与等高线距离太远,匹配概率极小且不宜一致性改正。水网流向与对应谷底线方向间夹角一般小于25°,在水网主支流交汇处可能偏大,因此设置匹配关系正确性检查角度阈值Δθ=30°。一致性检查时,考虑到水网与谷底线平均距离计算时以谷底点连线近似表示谷底线产生一定误差,当平均距离大于3 m且小于50 m时,认为两者不一致,并进行一致性改正。
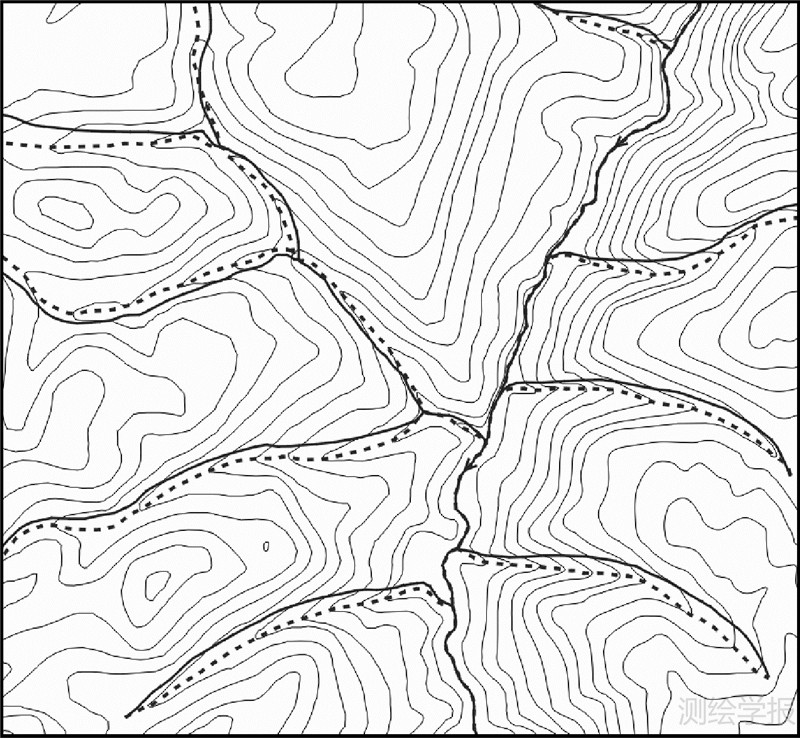
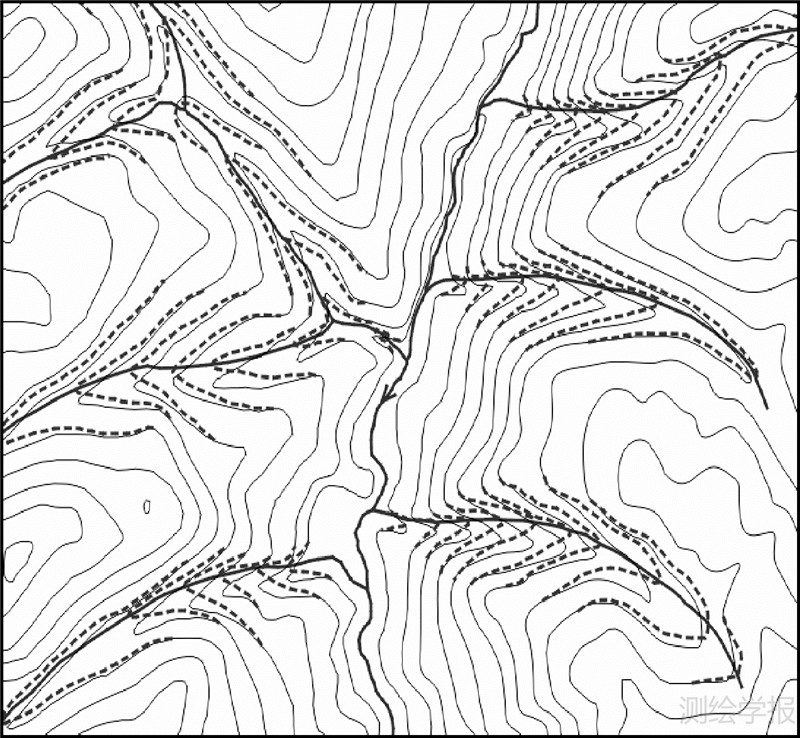
以人工检查的方式对试验结果进行统计分析。表 1是水网和等高线交点与谷底点匹配情况统计,匹配成功率达94.6%;一致性检查时,88.1%的河流线段与等高线不一致;表 2分析两种一致化改正方法的结果,两者成功率均达到90%以上。经分析发现,匹配一致化效果与水网和对应谷底线间的相对距离S及方向夹角Δθ密切相关,其中S=S1/S2,S1为水网与谷底线间距离,S2为谷底线对应“谷地片段”弯曲两开口端点间距离。对于S<0.25且Δθ<30°的区域,水网和等高线匹配一致化效果较好,等高线移位匹配水网后出现相邻等高线相交的情况相对较多,有待进一步改进。图 10、图 11分别是水网移位匹配等高线、等高线移位匹配水网效果图。
| 数量 | 正确 | 错误 | 正确率/(%) | |
| 水网和等高线交点 | 536 | 507 | 29 | 94.6 |
| 得到匹配谷底点的交点 | 508 | 483 | 25 | 95.1 |
| 未得到匹配谷底点的交点 | 28 | 24 | 4 | 85.7 |
| 数量 | 正确 | 错误 | 正确率/(%) | |
| 水网移位线段 | 416 | 389 | 27 | 93.5 |
| 等高线移位弯曲 | 442 | 401 | 41 | 90.7 |
|
|
图 10 水网移位匹配等高线
(虚线为匹配后水网) Fig. 10 The displacement of river network to match contour |
|
|
图 11 等高线移位匹配水网 (虚线为匹配后的等高线) Fig. 11 The displacement of contour to match river network |
从实际数据的试验结果分析,对于谷地特征较明显的山地区域,水网与等高线的匹配关系正确率较高,达到了94.6%,两种一致化改正方法较好地解决了数据间的不一致。
相比较同类要素的匹配,不同类要素间的匹配条件要少得多,需要利用空间分布知识将其间的匹配关系建立起来,进而完成数据间的一致性检测及改正。因此,这种空间分布知识的提取及规则化成为不同要素类数据匹配一致化的关键所在。
本研究需要进一步改进的内容包括:① 一致化改正的两种方法还需进一步改进,尤其是等高线移位匹配水网需挖掘更好的移位控制关系;② 针对线状水网与等高线间的匹配及一致化改正,可进一步扩展至面状水系要素(如面状湖泊、水库)与等高线间的匹配及一致化改正。
| [1] | GOODCHILD M F. Issues of Quality and Uncertainty[C]//Proceedings of State of Indiana Geographic Information System Conference. Indianapolis:Indiana University,1991:113-140. |
| [2] | CHEN Yumin, GONG Jianya, SHI Wenzhong. A Distance-based Matching Algorithm for Multi-scale Road Network[J]. Acta Geodaetica et Cartographica Sinica,2007,36(1):84-90.(陈玉敏,龚健雅,史文中.多尺度道路网的距离匹配算法研究[J].测绘学报,2007,36(1):84-90.) |
| [3] | ZHAO Dongbao, SHENG Yehua. Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J]. Acta Geodaetica et Cartographica Sinica,2010,39(4):416-421.(赵东保,盛业华.全局寻优的矢量道路网自动匹配方法研究[J].测绘学报,2010,39(4):416-421.) |
| [4] | BIRGIT K, HUANG W, HAUNERT J, et al. Matching River Datasets of Different Scales[C]// Proceedings of AGILE Conference .Berlin:[s.n.], 2009. |
| [5] | REVELL P, ANTOINE B. Automated Matching of Building Features of Differing Levels of Detail: a Case Study[C]//Proceedings of International Cartographic Conference 2009. Santiago:ICC, 2009. |
| [6] | HUH Y, YU K, HEO J. Detecting Conjugate-point Pairs for Map Alignment between Two Polygon Datasets[J]. Computer, Environment and Urban Systems, 2010,8(1):1-13. |
| [7] | HOPE S, KEALY A. Using Topological Relationships to Inform a Data Integration Process[J].Transactions in GIS,2008, 12(2):267-283. |
| [8] | MUSTIERE S, DEVOGELE T. Matching Networks with Different Levels of Detail [J]. GeoInformatic, 2008, 12(4): 435-453. |
| [9] | SAFRA E, KANZA Y, SAGIV Y. Location-based Algorithms for Finding Sets of Corresponding Objects over Several Geo-spatial Data Sets[J]. International Journal of Geographical Information Science, 2010, 24 (1):69-106. |
| [10] | DEVOGELE T, PARENT C, SPACCAPIETRA S. On Spatial Database Integration[J]. International Journal of Geographical Information Science, 1998, 12(4):335-352. |
| [11] | WALTER V, FRITSCH D. Matching Spatial Data Sets: a Statistical Approach[J]. International Journal of Geographical Information Science, 1999, 13(5):445-473. |
| [12] | AI Tinghua, WU Hehai. Consistency Correction of Shared Boundary between Adjacent Polygons[J]. Journal of Wuhan Technical University of Surveying and Mapping,2000, 25(5):426-431.(艾廷华,毋河海. 相邻多边形共享边界的一致化改正[J]. 武汉测绘科技大学学报, 2000, 25(5):426-431.) |
| [13] | TOBLER W R. A Computer Movie Simulating Urban Growth in the Detroit Region[J]. Economic Geography, 1970, 46:234-240. |
| [14] | LIU Wanzeng, CHEN Jun, DENG Kazhong, et al. Detecting the Spatial Inconsistency between the Updated Rivers and Valleys[J]. Journal of Image and Graphics,2008,13(5):1003-1008.(刘万增,陈军,邓喀中,等.数据库更新中河流与山谷线一致性检测[J].中国图象图形学报,2008,13(5):1003-1008.) |
| [15] | MARK D M. Automated Detection of Drainage Network from Digital Elevation Model[J]. Cartographica,1984,21(3):168-178. |
| [16] | O’CALLAGHAN J F, MARK D M. The Extraction of Drainage Networks from Digital Elevation [J]. Computer Vision, Graphics and Image Processing, 1984, 28(3):323-334. |
| [17] | AI Tinghua, ZHU Guorui, ZHANG Genshou. Extraction of Landform Features and Organization of Valley Tree Structure Based on Delaunay Triangulation Model[J]. Journal of Remote Sensing, 2003, 7(4):292-299. (艾廷华,祝国瑞, 张根寿. 基于Delaunay 三角网模型的等高线地形特征提取及谷地树结构化组织[J].遥感学报, 2003,7(4):292-299.) |
| [18] | TANG L. Automatic Extraction of Specific Geomorphological Elements from Contours [C]//Proceedings of the 5th SDH conference. Charleston:[s.n.],1992:554-556. |
| [19] | AI Tinghua, GUO Renzhong, LIU Yaolin. A Binary Tree Representation of Bend Hierarchical Structure Based on Gestalt Principles [C]//Proceedings of the 9th International Symposium on Spatial Data Handling. Beijing:[s.n.],2000. |