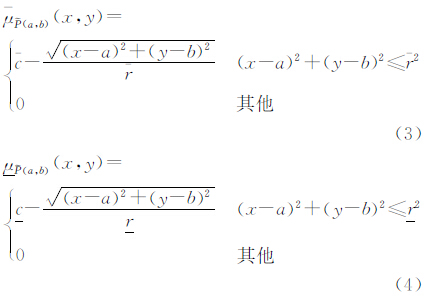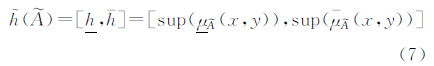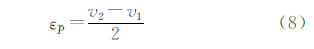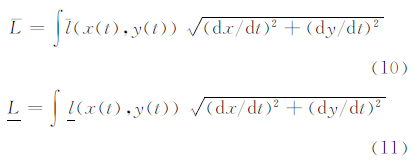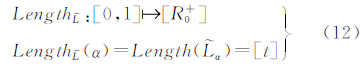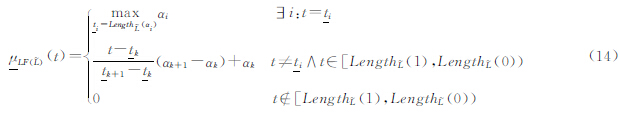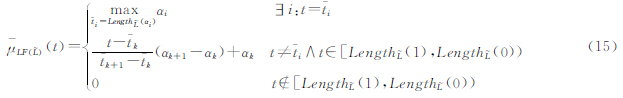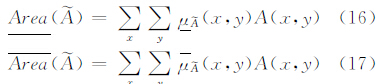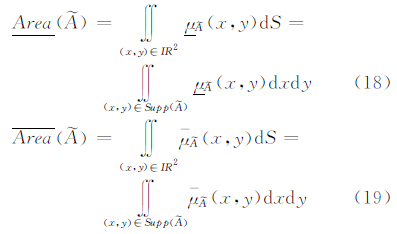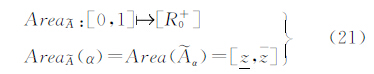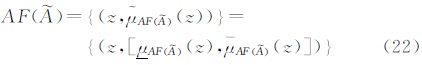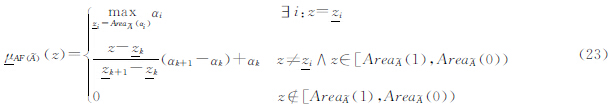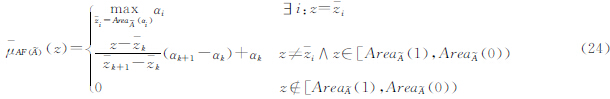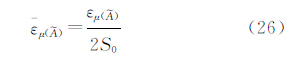2. 中国科学院 遥感应用研究所, 北京 100101
2. Institute of Remote Sensing Applications, Chinese Academy of Sciences, Beijing 100101, China
1 引 言
模糊性是复杂地理空间中许多现象和实体的共性,如自然灾害区域或孕灾环境的范围。对于空间对象的形状模糊性,许多文献用不同的词汇来描述:具有不确定边界的对象[1]、模糊空间对象[2]、宽边界对象[3]。模糊地理现象的描述方法可分为以下几种:① 从模糊边界的角度研究连续场中的模糊现象[4, 5];② 从模糊对象的角度,包括三值逻辑[6]、模糊逻辑[7, 8, 9];③ 基于其他理论的模糊空间现象建模,包括粗糙集理论和灰集理论[10, 11, 12, 13],基于这些模型讨论了模糊对象的拓扑、方向、距离等空间关系。这些表达方法或模型存在的共同缺陷是只能表达单一尺度下的地理特征而不能表达模糊地理现象在适宜尺度区间内的状态,同时也不能表达由测量数据误差等方面引起的隶属度误差。
模糊逻辑方法是模糊地理现象建模和分析的主要方法,但是由于经典的模糊集理论以精确值表示隶属度而不能度量隶属度误差,一直受到国内外学者的质疑。为了克服这一缺陷,文献 [14] 提出n阶模糊集(type n fuzzy sets)的概念,目前应用较多的是Ⅱ-型模糊集(type-Ⅱ fuzzy sets),Ⅱ-型模糊系统理论已在通信、金融、控制及医疗等许多领域取得了成功应用[15],Ⅱ-型模糊集以主隶属度表示对象属性的模糊性,以次隶属度描述主隶属度的不确定性,使得对不确定性的处理能力大大增强。区间Ⅱ-型模糊集(interval type-Ⅱ fuzzy sets)是次隶属度为1时的特殊的Ⅱ-型模糊集,大大降低了Ⅱ-型模糊集的复杂性,应用最为广泛。一些研究人员认为GIS中广泛存在高阶模糊性[16, 17, 18, 19],研究高阶模糊地理现象时大多采用区间Ⅱ-型模糊集[19, 20, 21]。
地理空间数据存在误差,由这些数据模糊化得到的模糊隶属度也应存在误差,文献 [22] 基于空间数据的位置误差推导了模糊地理实体隶属度的误差模型,给出隶属度误差的度量方法;在不同尺度下进行模糊化得到的模糊隶属度也可能不同。认为尺度效应和测量误差是客观上造成模糊隶属度误差的主要方面;解析模糊地理对象时专家知识的不确定性、部门间标准的差异性以及作业人员的主观判断是造成模糊隶属度误差的主观因素。现有的模型不能满足高阶地理现象的建模和分析,本文基于区间Ⅱ-型模糊集构建一个模糊地理对象模型,研究模糊线长度和模糊面面积的度量方法,并讨论区间Ⅱ-型模糊对象隶属度误差的描述方法。
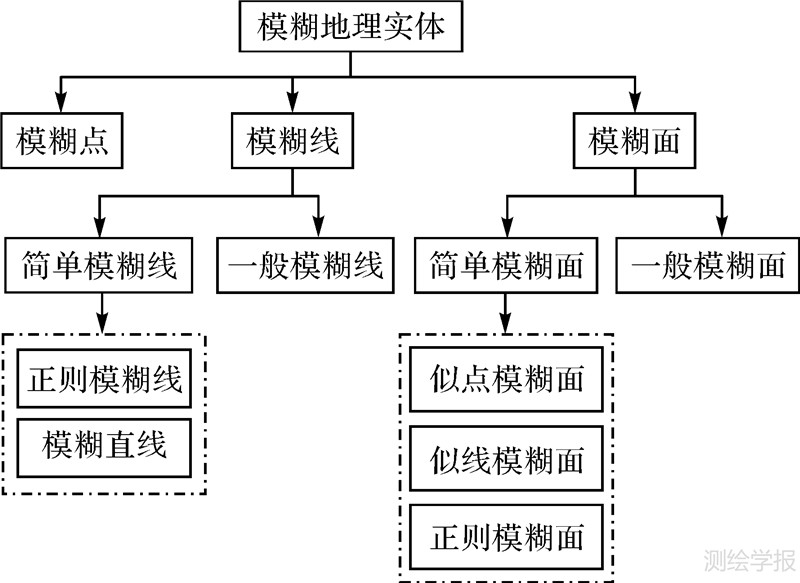
2 基于区间Ⅱ-型模糊集模糊对象表达与定义基于区间Ⅱ-型模糊集的模糊地理对象模型由区间Ⅱ-型模糊点、区间Ⅱ-型模糊线和区间Ⅱ-型模糊面组成,如图 1。本文采用文献 [23] 定义的区间Ⅱ-型模糊集的拓扑空间。设X为非空集合,I为区间 [0,1],τ为X上的区间Ⅱ-型模糊集簇,满足: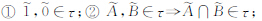
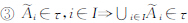 。
。
|
| 图 1 基于区间Ⅱ-型模糊集的模糊对象模型的结构 Fig. 1 Structure of fuzzy object model based on interval type-Ⅱ fuzzy sets |
则称(X,τ)为区间Ⅱ-型模糊集的一个模糊拓扑空间,τ为一个区间Ⅱ-型模糊拓扑。
2.1 模糊点实体简单模糊点表示模糊拓扑空间(X,τ)中位置 (a,b)(a,b∈R2)上具有某种属性,但是只能在一定程度上确定,如图 2( a )所示,定义为
(a,b)(a,b∈R2)上具有某种属性,但是只能在一定程度上确定,如图 2( a )所示,定义为

|
| 图 2 区间Ⅱ-型模糊点 Fig. 2 Interval type-Ⅱ fuzzy point |
模糊点群是由有限多个简单模糊点组成,可以表示成{ i(ai,bi)},1≤i≤n。
i(ai,bi)},1≤i≤n。
区间Ⅱ-型模糊线实体是一种没有宽度(大小)但是线上任意点的隶属度可能不能完全确定的线状实体。例如2008年汶川地震中破坏的公路可用这种实体描述其受损程度。区间Ⅱ-型模糊线的隶属度由上隶属函数(upper membership function,UMF)和下隶属函数(lower membership function,LMF)度量,表示为 (x,y)和
(x,y)和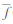 (x,y),且
(x,y),且 (x,y)≤
(x,y)≤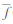 (x,y)。先定义简单区间Ⅱ-型模糊线。
(x,y)。先定义简单区间Ⅱ-型模糊线。
(1) 简单模糊线是指在模糊拓扑空间(X,τ)中满足以下条件的区间Ⅱ-型模糊线:① 简单模糊线在X-Y平面上的投影为线实体;② 简单模糊线的UMF和LMF曲线是三维曲线;③ 简单模糊线的UMF和LMF曲线是连续的;④ 简单模糊线的UMF和LMF曲线是凸的;⑤ 简单模糊线是一个闭集;⑥ 简单模糊线的闭包是紧的。在这些条件中,③ 保证线上属性的连续性;④ 使得模糊线的任意截集都是连续线实体;⑤和⑥要求简单模糊线闭合且有界,同时要求简单模糊线不是由两个或多个独立的模糊线实体构成,这样有利于界定模糊线的边界部分。简单模糊线包括模糊直线、折线、环线、多线、曲线等(图 3),模糊曲线在X-Y平面上的投影为曲线,本文仅讨论前4种。首先定义两种特殊的简单模糊线:模糊直线在 GIS 中通常以两个点分别表示直线的起点和终点,那么简单模糊直线也可以用两个点来分别定义其起点和终点,并且定义其上下隶属函数,如图 3( b )所示,在X-Y平面上的投影为直线;正则简单模糊线是一个区间Ⅱ-型模糊数[3 ,4]。

|
| 图 3 5类区间Ⅱ-型模糊线 Fig. 3 Five type’s interval type-Ⅱ fuzzy line |
(2) 简单模糊线群是简单模糊线的集合。当模糊线段首尾相连时称为模糊折线,即第i条简单模糊线与第i+1条邻接,在连结处有 i,2=
i,2=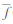 i+1,1,
i+1,1, i,2=
i,2=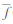 i+1,1。当
i+1,1。当 n,2=
n,2= 1,1且
1,1且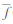 n,2=
n,2=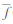 1,1时为模糊环线。模糊多线由简单模糊线、模糊折线或模糊环线构成。图 3中( c)、(d)和(e )分别为模糊折线、模糊环线和模糊多线。
1,1时为模糊环线。模糊多线由简单模糊线、模糊折线或模糊环线构成。图 3中( c)、(d)和(e )分别为模糊折线、模糊环线和模糊多线。
(3) 一般模糊线是指UMF和LMF 不一定连续和凸的,但应是闭集,包括模糊曲线。本文不对一般模糊线展开讨论。
2.3 模糊面实体区间Ⅱ-型模糊面实体S通过上隶属函数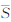 (x,y)和下隶属函数
(x,y)和下隶属函数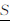 (x,y)来描述。文献[21] 定义Ⅱ-型模糊点和线,事实上这两类实体分别是“点状面”和“线状面”,即本质上还是面实体,例如某些污染源和动物迁移路径。鉴于此将这两类特殊的模糊面分别定义为“似点模糊面”和“似线模糊面”。
(x,y)来描述。文献[21] 定义Ⅱ-型模糊点和线,事实上这两类实体分别是“点状面”和“线状面”,即本质上还是面实体,例如某些污染源和动物迁移路径。鉴于此将这两类特殊的模糊面分别定义为“似点模糊面”和“似线模糊面”。
模糊拓扑空间(X,τ)中满足以下条件的区间Ⅱ-型模糊面称为简单模糊面:① 简单模糊面是凸的,即LMF和UMF均是凸的;② 简单模糊面的LMF和UMF是上半连续的;③ 简单模糊面是一个闭集;④ 简单模糊面的闭包是紧的。
与简单模糊线的性质相似,① 使得模糊面的任意截集都是连续面实体,同时简单模糊面最多只有一个核区域;③和④同时要求简单模糊面不是由两个或多个独立的模糊面域构成,简单模糊面不存在空洞。在此定义3种特殊的简单模糊面:似点模糊面、似线模糊面和正则简单模糊面。
2.3.2 似点模糊面似点模糊面表示在有限范围内,具有某种属性的区域。之所以称为“似点模糊面”,是因为这种实体从认知的角度看,在一定尺度下该类实体具有点的特征,但是在一定的截集水平下又具有面的特征。以参考点 (a,b)(a,b∈R2)为中心,与
(a,b)(a,b∈R2)为中心,与 (a,b)越近就越具有某种属性。例如在农作物发生病虫灾害时,庄稼地呈现出一个小的病虫害斑块,中间点最严重,然后向四周逐渐减弱,因此如果关注的尺度比较小时是一个小的斑块(模糊面),当关注的尺度较大时表现为一个模糊点。似点模糊面形式化描述为
(a,b)越近就越具有某种属性。例如在农作物发生病虫灾害时,庄稼地呈现出一个小的病虫害斑块,中间点最严重,然后向四周逐渐减弱,因此如果关注的尺度比较小时是一个小的斑块(模糊面),当关注的尺度较大时表现为一个模糊点。似点模糊面形式化描述为
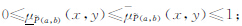
 和
和 分别为某种属性的下隶属度和上隶属度的最大值,表示其中心隶属度,有0≤
分别为某种属性的下隶属度和上隶属度的最大值,表示其中心隶属度,有0≤ ≤
≤ ≤1;
≤1;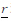 和
和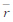 分别表示地理空间中属性可能存在的最小和最大范围的半径,0<r≤
分别表示地理空间中属性可能存在的最小和最大范围的半径,0<r≤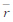 。
。
当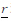 =
=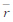 =0时,似点模糊面转化为简单模糊点,此时当
=0时,似点模糊面转化为简单模糊点,此时当 =
= =1时,为经典点集拓扑空间中的分明点( crisp point );当上、下隶属度相等时转化为Ⅰ-型模糊点;当
=1时,为经典点集拓扑空间中的分明点( crisp point );当上、下隶属度相等时转化为Ⅰ-型模糊点;当 =
= =1时称
=1时称 (a,b)为核。可以看出在无限Ⅱ-型拓扑空间中,似点模糊面由无穷多的简单模糊点构成。当“似点模糊面”的
(a,b)为核。可以看出在无限Ⅱ-型拓扑空间中,似点模糊面由无穷多的简单模糊点构成。当“似点模糊面”的 =
= =λ时,
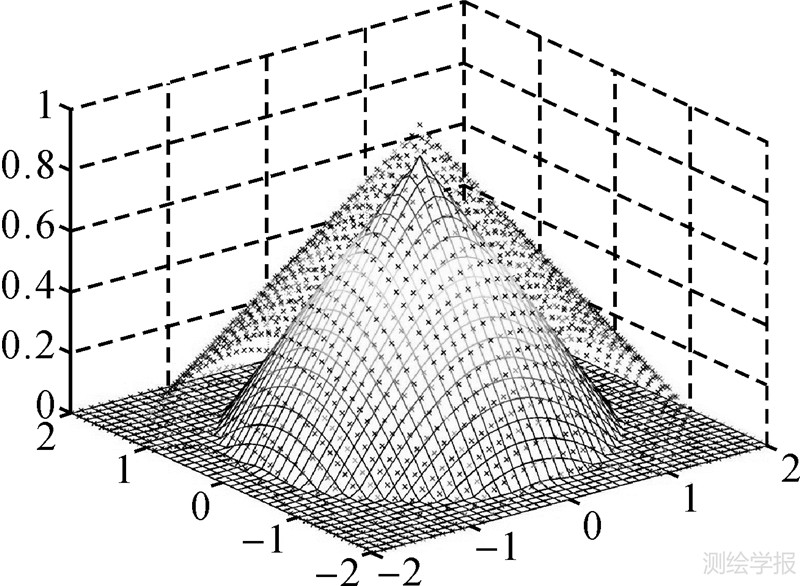
=λ时, λ(a,b)=P(a,b),此时似点模糊面转换为分明集中的点,因此具有点的特征(图 4)。
λ(a,b)=P(a,b),此时似点模糊面转换为分明集中的点,因此具有点的特征(图 4)。
|
| 图 4 区间Ⅱ-型似点模糊面 Fig. 4 Interval type-Ⅱ point-like fuzzy region |
与“似点模糊面”类似,是因为这种实体从认知的角度看,在一定尺度下该类实体具有线状实体的特征,但是在一定的截集水平下又具有面的特征。
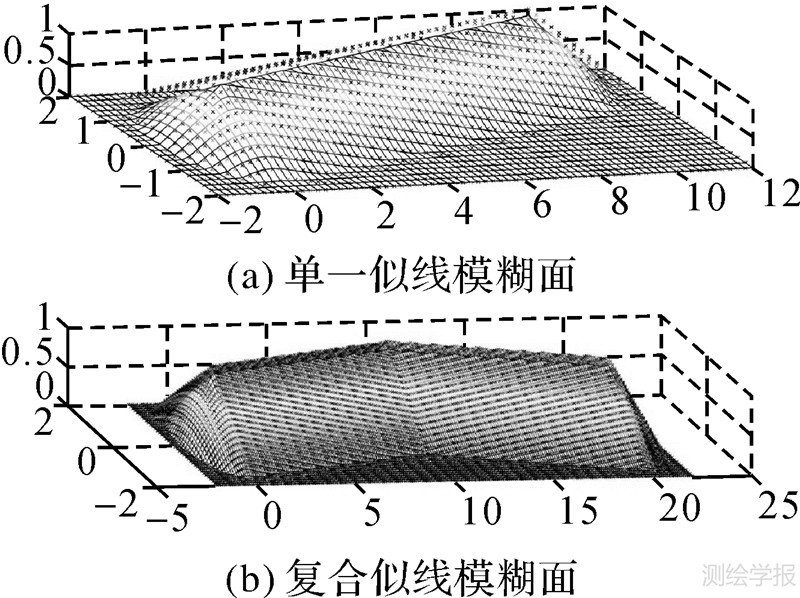
单一似线模糊面是由无限“似点模糊面”构成的有序集合,显然所有“似点模糊面”的中心构成一条简单模糊线。如图 5(a)所示,单一似线模糊面可形式化表示为
|
| 图 5 区间Ⅱ-型似线模糊面 Fig. 5 Interval type-Ⅱ linelike fuzzy region |
复合似线模糊面则为单一似线模糊面的并集,如图 5( b )
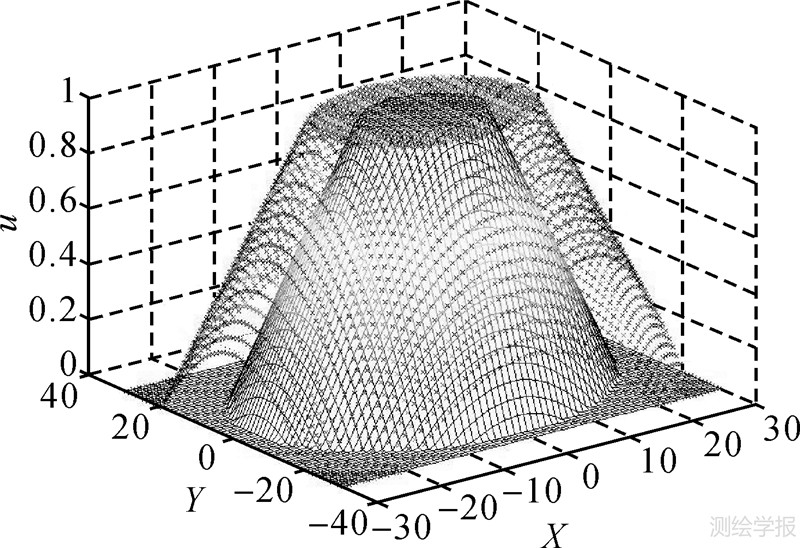
2.3.4 正则简单模糊面正则简单模糊面是一个区间Ⅱ-型模糊数,图 6和图 7分别表示离散空间和连续空间中的正则简单模糊面,因此正则简单模糊面除了满足简单模糊面的条件外,还需满足以下条件:① 正则简单模糊面是一个区间Ⅱ-型模糊数;② 正则简单模糊面的内部、核和外层是双连通的规则开集。

|
| 图 6 离散空间中的正则简单模糊面 Fig. 6 The normal simple interval type-Ⅱ fuzzy region in discrete space |
|
| 图 7 连续空间中的正则简单模糊面 Fig. 7 The normal simple interval type-Ⅱ fuzzy region in infinite space |
对于一个非空区间Ⅱ-型模糊集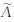 ,高定义如下
,高定义如下
显然对于一个简单的区间Ⅱ-型模糊点,其高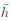 (
(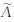 )=[v1,v2]。对于区间Ⅱ-型模糊点群,
)=[v1,v2]。对于区间Ⅱ-型模糊点群,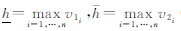 (类似的可以定义区间Ⅱ-型模糊线和面的高)。模糊点的隶属度误差为
(类似的可以定义区间Ⅱ-型模糊线和面的高)。模糊点的隶属度误差为
文献 [8] 通过长度积分法来确定对Ⅰ-型模糊线的长度,得到的长度是一个确切值,这跟模糊的本质不符。设Ⅱ-型模糊线如图 3( a )所示,设图中X-Y平面上量纲为 m 。模糊线的 UMF和LMF 分别表示为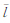 (x,y)和
(x,y)和 (x,y),为计算方便,可以表示成参数t的方程
(x,y),为计算方便,可以表示成参数t的方程 (x(t),y(t))和
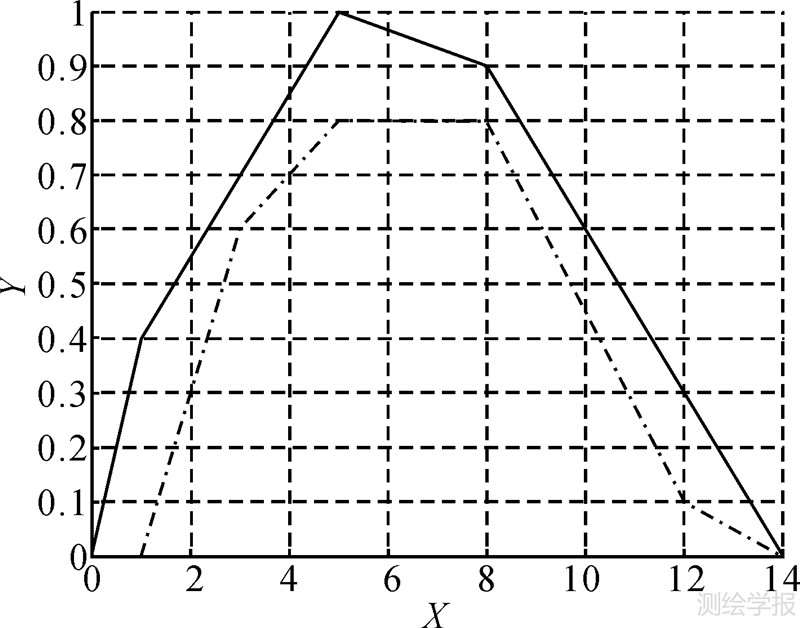
(x(t),y(t))和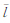 (x(t),y(t)),在直线方向上的隶属函数如图 8所示,本文给出以下几种度量方法。
(x(t),y(t)),在直线方向上的隶属函数如图 8所示,本文给出以下几种度量方法。
式中,长度单位与X-Y平面上的单位一致(后文长度公式的单位也等同于X-Y平面上的长度单位,不再特别说明)。于是模糊长度可表示为
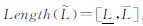 。
。
|
| 图 8 区间Ⅱ-型模糊线的隶属函数 Fig. 8 Membership function of interval type-Ⅱ fuzzy line |
区间Ⅱ-型模糊线的α-截集可表示为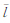 α(x,y)和
α(x,y)和 α(x,y),根据模糊长度的计算方法即可确定其α-截集长度:
α(x,y),根据模糊长度的计算方法即可确定其α-截集长度: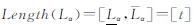 ,因此从α-截集的角度给出了模糊线的长度描述方法
,因此从α-截集的角度给出了模糊线的长度描述方法
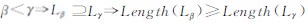 。同时对于任意一个αi存在一个
。同时对于任意一个αi存在一个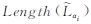 与其对应,因此通过
与其对应,因此通过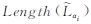 和αi可以定义长度和长度隶属度的关系。区间Ⅱ-型模糊线
和αi可以定义长度和长度隶属度的关系。区间Ⅱ-型模糊线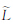 的长度可以表示为一个区间Ⅱ-型模糊集
式中,
的长度可以表示为一个区间Ⅱ-型模糊集
式中, 由下式确定
式中,
由下式确定
式中, ,
,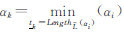 式中,
式中,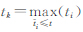 ,并且
,并且 。
3.2.3 绝对长度
。
3.2.3 绝对长度指隶属度为1时模糊直线的长度,也可以认为 1(x,y)的长度。
1(x,y)的长度。
其模糊概略长度、α-截集长度均由模糊区间数表示,长度误差表示为 ,单位与长度单位一致;对于绝对长度,如果存在
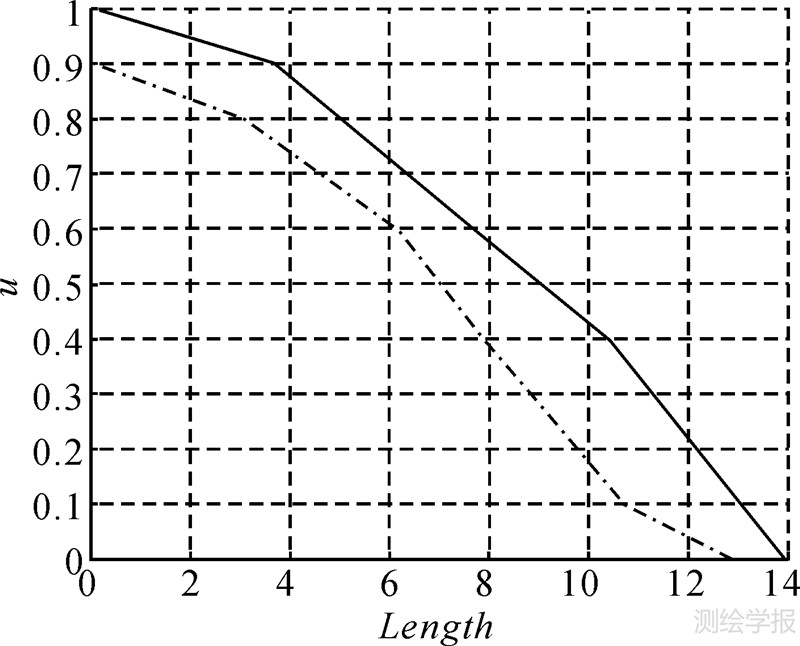
,单位与长度单位一致;对于绝对长度,如果存在 1(x,y)大于0,那么隶属度为1时为分明线。图 3( a)确定的直线的概略长度为[6.3,8.55](单位:m);绝对长度为0 m ;α-截集长度如表 1和图 9所示。
1(x,y)大于0,那么隶属度为1时为分明线。图 3( a)确定的直线的概略长度为[6.3,8.55](单位:m);绝对长度为0 m ;α-截集长度如表 1和图 9所示。
| α | 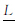 α/m α/m |
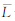 α/m α/m
|
| 0.005 | 12.800 | 13.900 |
| 0.1 | 10.700 | 13.100 |
| 0.2 | 9.800 | 12.200 |
| 0.3 | 8.900 | 11.300 |
| 0.4 | 7.900 | 10.400 |
| 0.5 | 7.100 | 9.000 |
| 0.6 | 6.200 | 7.700 |
| 0.7 | 4.600 | 6.400 |
| 0.8 | 3.100 | 5.000 |
| 0.9 | 0 | 3.700 |
| 0.95 | 0 | 1.900 |
| 1 | 0 | 0.100 |
|
| 图 9 区间Ⅱ-型模糊线的长度 Fig. 9 Length of interval type-Ⅱ fuzzy line |
面积是模糊地理实体很重要的一个属性,在宽边界描述方法中以最大范围和最小范围来表示。文献[25] 给出了离散空间中Ⅰ-型模糊实体面积的度量方法。文献 [26] 分析了这种方法,并从α-截集的角度研究模糊区域的面积描述方法。这两种方法的共同缺陷是以一个精确值表示模糊实体的面积。笔者给出两种区间Ⅱ-型模糊区域的面积度量方法。
3.3.1 三维体积法设区间Ⅱ-型模糊区域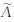 ,由平面X-Y和隶属度μ
,由平面X-Y和隶属度μ 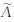 (x,y)构成两个三维实体,那么该实体的体积为区间Ⅱ-型模糊区域的面积Area(·)。在离散空间中
(x,y)构成两个三维实体,那么该实体的体积为区间Ⅱ-型模糊区域的面积Area(·)。在离散空间中
区间Ⅱ-型模糊区域的截集为一个宽边界区域,内部区域为一个确定的α-截集区域,而宽边界区域为不确定区域,避免了在Ⅰ-型模糊集中α-截集为确定区域的缺陷。从α-截集的角度给出了模糊区域的面积描述方法
因此可以得到区间Ⅱ-型模糊区域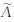 的面积定义
式中,
的面积定义
式中, 可用式(23)、(24)确定
式中,
可用式(23)、(24)确定
式中,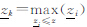 ,并且
,并且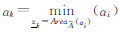 式中,
式中,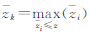 ,并且
,并且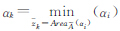 。
。
在图 7中,设X-Y平面上的长度单位为 m ,用三维体积法确定图 7的区间Ⅱ-型模糊面的面积为[1 102.7,2 167],单位为 m 2;用α-截集法确定的面积如表 2和图 10所示。
| α | 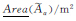 |

|
| 0.005 | 2261 | 3493 |
| 0.1 | 2001 | 3353 |
| 0.2 | 1725 | 3145 |
| 0.3 | 1473 | 2821 |
| 0.4 | 1229 | 2453 |
| 0.5 | 1009 | 2121 |
| 0.6 | 829 | 1793 |
| 0.7 | 657 | 1517 |
| 0.8 | 497 | 1257 |
| 0.9 | 365 | 1009 |
| 0.95 | 305 | 901 |
| 1 | 253 | 797 |
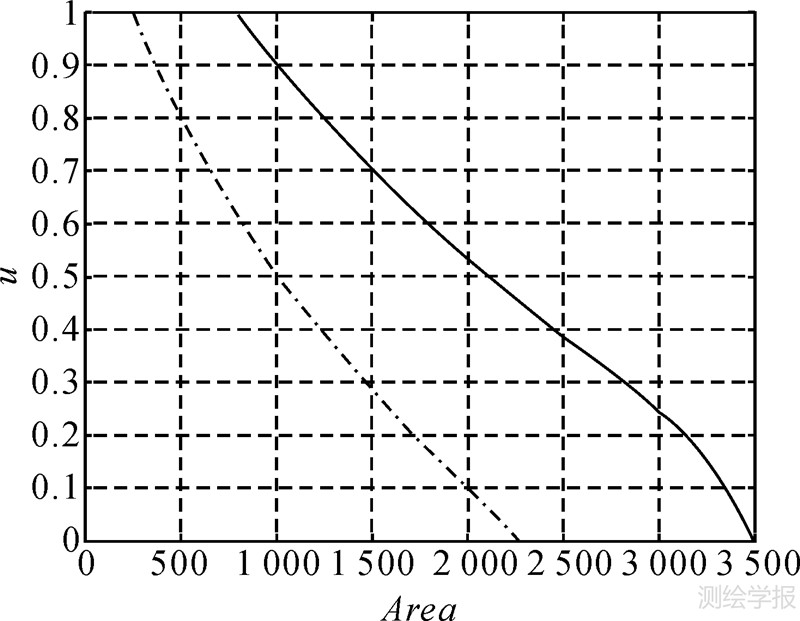
|
| 图 10 区间Ⅱ-型模糊区域的面积 Fig. 10 Area of interval type-Ⅱ fuzzy region |
大量的模糊实体难以定义其几何结构,如通过遥感手段获取的森林区域。假定模糊现象的上隶属函数和下隶属函数已知,由这两个隶属度函数可以定义区间Ⅱ-型模糊区域的不确定性立方体,由此可确定绝对隶属度误差和相对隶属度误差。设区间Ⅱ-型模糊区域支集的面积为 S0,栅格单元的面积为S,上下隶属函数为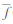 (i,j)和
(i,j)和 (i,j),不确定性可用如下公式度量,单位与面积单位一致。
(i,j),不确定性可用如下公式度量,单位与面积单位一致。
绝对隶属度误差
平均隶属度误差
4 结 论客观地对模糊地理现象建模和度量是分析模糊自然现象的前提,本文讨论基于区间Ⅱ-型模糊集的模糊地理对象建模、度量和不确定性等方面的关键理论,克服了现有模型和度量方法的缺陷,为高阶模糊地理信息理论提供了一种可行的研究思路。本文提出的“似线模糊面”和“似点模糊面”在本质上是模糊面,只是在认知层面上像“线”和“点”,因此二者均用模糊面的面积及其隶属度误差进行度量。本文提出的理论方法的客观性和应用效果有待进一步验证和评价。
| [1] | BURROUGH P A, FRANK A U, et al. Geographic Objects with Indeterminate Boundaries [M]. London: Taylor and Francis,1996. |
| [2] | DILO A. Representation of and Reasoning with Vagueness in Spatial Information: a System for Handling Vague Objects [D]. Enschede: ITC,2006. |
| [3] | CLEMENTINI E, FELICE P. A Spatial Model for Complex Objects with a Broad Boundary Supporting Queries on Uncertain Data [J]. Data and Knowledge Engineering, 2001,37:285-305. |
| [4] | LIU Wenbao, DENG Min, YI Tong. Analyses of Fuzzy Geographic Boundary in Vector GIS[J].Journal of Shandong University of Science and Technology (Natural Science),2000,19(1):28-32.(刘文宝,邓敏,易彤.矢量GIS中模糊地理边界的分析[J].山东科技大学学报:自然科学版,2000,19(1):28-32.) |
| [5] | SUNILAL R, LAINE E, KREMENOVA O. Fuzzy Model and Kriging for Imprecise Soil Polygon Boundaries [C] //Proceedings of 1st International Conference on Advances in Mineral Resources Management and Enviromental Geotechnology. Hania: [s.n.],2004. |
| [6] | BEJAOUI L, PINET F, BEDARD Y,et al. Qualified Topological Relations between Spatial Objects with Possible Vague Shape [J]. International Journal of Geographical Information Science,2009,23(7):877-921. |
| [7] | TANG Xinming. Spatial Object Modeling in Fuzzy Topological Spaces with Applications to Land Cover Change [D]. Wageningen: University of Twente, 2004. |
| [8] | LIU K, SHI Wenzhong. Quantitative Fuzzy Topological Relations of Spatial Objects by Induced Fuzzy Topology [J]. International Journal of Applied Earth Observation and Geoinformation, 2009, 11(1): 38-45. |
| [9] | HE Jianhua, LIU Yaolin, YU Yan,et al.The Topological Relation Model for Indeterminate Geographical Objects Based on Fuzzy Close-degree[J].Acta Geodaetica et Cartographica Sinica,2008,37(2):212-216.(何建华,刘耀林,俞艳, 等.基于模糊贴近度分析的不确定拓扑关系表达模型[J].测绘学报,2008,37(2):212-216.) |
| [10] | DENG Min,LI Zhilin,CHENG Tao. Rough-set Representation of GIS Data Uncertainties with Multiple Granularities[J]. Acta Geodaetica et Cartographica Sinica,2006,35(1):64-70.(邓敏,李志林,程涛.多粒度的GIS数据不确定性粗集表达[J].测绘学报,2006,35(1):64-70.) |
| [11] | LI Dajun,LIU Bo,CHENG Penggen, et al.Description of Topological Relation for Fuzzy Spatial Objects Based on Rough Set[J]. Acta Geodaetica et Cartographica Sinica,2007,36(1):72-77.(李大军,刘波,程朋根,等.模糊空间对象拓扑关系的Rough描述[J].测绘学报,2007,36(1):72-77.) |
| [12] | GAO Zhenji, WU Lun, YANG Jian. Representaion of Topological Relations between Vague Objects Based on Rough and RCC Model [J]. Aeta Scientiarum Naturalium Universitatis Pekinensis,2008,44(4):596-603.(高振记,邬伦,杨俭.基于RCC及粗糙模型的模糊地理对象拓扑关系表达[J].北京大学学报:自然科学版,2008,44(4):596-603.) |
| [13] | BAO Lei, QIN Xiaolin. Uncertain Spatio-temporal Data Model Based on Grey Sets[J].Journal of Remote Sensing, 2005,9(6):645-652.(包磊,秦小麟.基于灰集的不确定性时空数据模型[J].遥感学报,2005,9(6):645-652.) |
| [14] | ZADEH L. The Concept of a Linguistic Variable and Its Application to Approximate Reasoning[J].Information Sciences, 1975,8(3):199-249. |
| [15] | ZHENG Gao,XIAO Jian,JIANG Qiang,et al.Research on Theory and Application of Type-2 Fuzzy Logic Systems[J].Journal of Hefei University of Technology,2009,32(7):966-971.(郑高,肖建,蒋强,等.二型模糊系统理论与应用[J].合肥工业大学学报:自然科学版,2009,32(7):966-971.) |
| [16] | KULIK L. Spatial Vagueness and Second-order Vagueness [J].Spatial Cognition and Computation, 2003,3(2-3),157-183. |
| [17] | CHENG Tao, FISHER P, LI Zhilin. Double Vagueness: Uncertainty in Multi-scale Fuzzy Assignment of Duneness[J].Geo-spatial Information,2004,7(1):58-66. |
| [18] | FISHER P, ARNOT C, WADSWORTH R,et al. Detecting Change in Vague Interpretations of Landscapes [J].Ecological Informatics,2006,1(2),163-178. |
| [19] | FISHER P, CHENG Tao, WOOD J. Higher Order Vagueness in Geographical Information:Empirical Geographical Population of Type n Fuzzy Sets[J]. Geoinformatica , 2007,11(3):311-330. |
| [20] | FISHER P, ARNOT C. Mapping Type 2 Change in Fuzzy Land Cover[C]//Proceedings of the NATO Advanced Research Workshop on Fuzziness and Uncertainty in GIS for Environmental Security and Protection. Kyiv:[s.n.],2007:167-186. |
| [21] | DU Guoning, ZHU Zhongying. Modelling Spatial Vagueness Based on Type-2 Fuzzy Set[J].Journal of Zhejiang University Science A,2006,7(2):250-256. |
| [22] | GUO Jifa,CUI Weihong,LIU Zhen,et al. Investigation of Uncertainty Integrative Description on Fuzzy Geographical Object[J]. Geomatics and Information Science of Wuhan University,2010,35(1):46-50.(郭继发,崔伟宏,刘臻,等.模糊地理实体不确定性综合描述研究[J].武汉大学学报:信息科学版,2010,35(1):46-50.) |
| [23] | MONDA T K,SAMANTA S K. Topology of Interval-Valued Fuzzy Sets[J]. Indian Journal of Pure and Applied Mathematics, 1999,30(1):23-38. |
| [24] | WANG Guijun,LI Xiaoping.Correlation and Information Energy of Interval Valued Fuzzy Numbers[J].Fuzzy Sets and Systems,1999,103(1):169-175. |
| [25] | ROSENFELD A. The Diameter of a Fuzzy Set [J]. Fuzzy Sets and Systems, 1984, 13(3): 241-246. |
| [26] | FONTE C C, LODWICK W A. Areas of Fuzzy Geographical Entities [J].International Journal of Geographical Information Science,2004,18(2):127-150. |