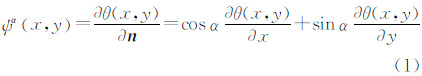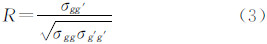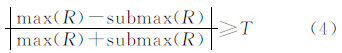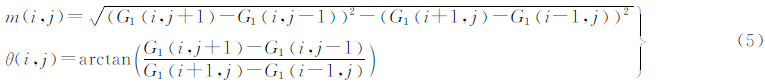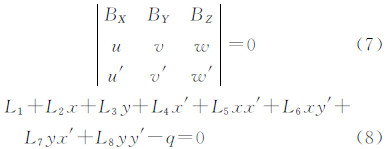1 引 言
立体影像匹配是数字摄影测量的核心技术之一。常用立体影像匹配算法,如跨接法匹配、核线匹配、最小二乘匹配[1]在地形信息自动生成中效果明显。但对于建筑物的三维信息自动生成,上述算法效果还不明显。文献[2]提出的基于小波变换、遗传算法和最小二乘匹配的高精度影像匹配组合算法,其小波变换用于减少匹配搜索数据,遗传算法用于优化搜索空间,最小二乘匹配则用于获得子像素匹配精度。文献[3]提出的全局自动配准算法,采用多分辨率小波变换缩小搜索空间,实现多传感器、大数据量影像的快速高效自动配准。当影像间视差不连续,或存在明显辐射强度变化,或有较大旋转变化时,上述算法的匹配效果明显下降。Fourier-Mellin变换是保持旋转、尺度和平移不变性算法,在SAR与多光谱影像配准,医学影像匹配中得到应用[6, 7, 8] 。Fourier-Mellin影像匹配算法属于一致性尺度不变算法,用于存在中心投影变形的影像匹配还存在一些问题待解决。文献[9]提出SIFT(scale-invariant feature transform)算法,对于不同传感器影像配准、地面立体影像匹配,具有辐射强度与尺度不变性。但是,SIFT算法的高斯多尺度变换以及128维向量匹配,计算量大、效率低,已经影响到其实际应用。
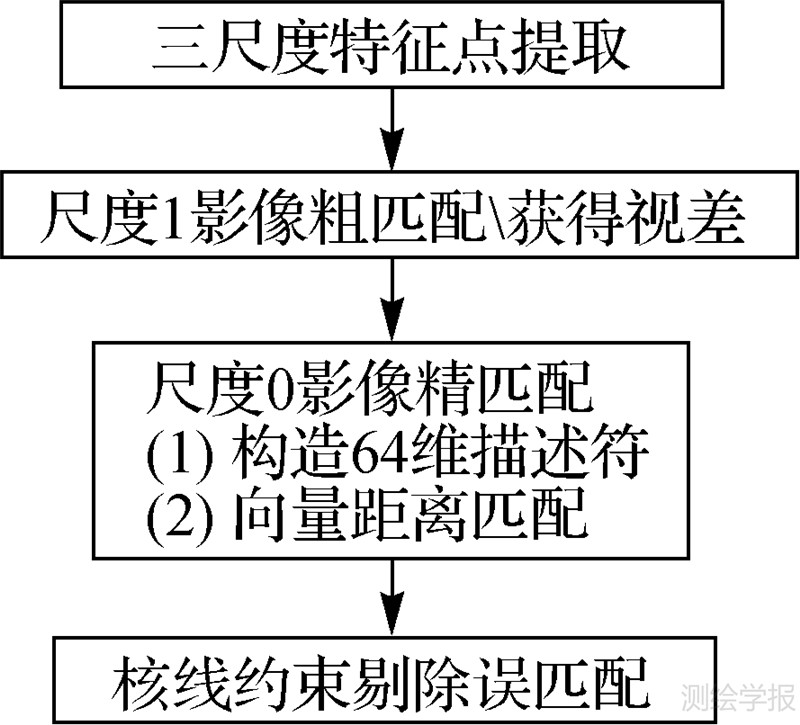
针对上述问题,本文提出了一种新的尺度与旋转不变性匹配算法,其基本思路是利用方向小波变换构造三尺度特征点算子,保证特征提取的尺度与辐射强度不变。采用两尺度立体匹配,解决匹配中尺度不变性问题;在精匹配中,构造特征点的主方向与64维描述向量,解决匹配中旋转不变性问题。算法流程如图 1所示。
|
| 图 1 算法流程 Fig. 1 The algorithmic flow chart |
为解决影像特征提取中辐射强度与尺度不变性,基于多尺度方向小波变换,构造多尺度小波特征算子,在3个尺度下进行特征点提取。
2.1 二维方向小波构造二维光滑函数θ(x,y)沿方向 n=[cos αsin α]的一阶偏导数为[5]
对于任意函数f(x,y),有方向小波变换
式中,α表示方向小波变换后高频信息方向。 2.2 生成三尺度小波影像采用样条小波,基于式(2)对数字影像G(m,n)进行二尺度离散方向小波变换,分别得到三尺度下影像:
尺度0 低频影像 G0
尺度1 低频影像 G1
高频影像 D10、D145、D190、D1135
尺度2 低频影像 G2
高频影像 D20、D245、D290、D2135

|
| 图 2 离散方向小波多尺度变换 Fig. 2 Multi-scale transform of directional wavelet |
三尺度特征点算子构造如下:
由尺度2高频影像得
由尺度1 高频影像得
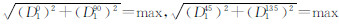
由尺度0 低频影像得
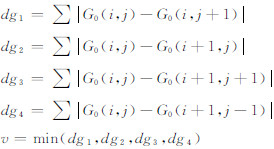
式中,dg1、dg2、dg3、dg4 分别为水平、垂直、倾斜方向的灰度差分绝对值和,三尺度下同时满足条件的点为特征点。
尺度与旋转不变性立体匹配分为两步进行。首先在尺度1低频影像G1上作粗匹配,得到左右影像间视差;然后在尺度0低频影像G0上构造特征点主方向和64维描述向量,进行向量距离匹配。
3.1 基于特征的粗匹配在尺度1左右低频影像上,利用公式(3)计算左、右影像特征点的灰度相关系数
式中,σgg′为左右影像灰度协方差。对于左像上任一特征点,在右像上可找到其最大相关系数max(R)、次大相关系数submax(R)所对应的点。取满足式(4)的点对 作为粗匹配点。通过试验,选取T在0.5~0.8 之间。 3.2 特征点梯度主方向确定在G0影像选定特征点邻域,计算邻域内梯度模m与梯度方向θ
将邻域内梯度方向0°≤θ(i,j)≤360°
按每10°划分,统计邻域内梯度直方图,其峰值即为该特征点的主方向。 3.3 构造64维特征描述向量在G0影像上构造64维特征描述符,保持特征点邻域窗口的0°方向与主方向重合。
定义邻域窗口为以特征点为中心8个同心环,将环域分为8方向(0°、45°、90°、135°、180°、225°、270°、315°)。 如图 3所示,以一特征点为中心取17×17像素的窗口,依次建立8层环形区域。由式(5)计算每个像素的梯度模和方向,统计每环内8个方向的梯度累加值。构建8×8=64维的特征向量。

|
| 图 3 构造64维特征描述向量 Fig. 3 The describing vector of 64 parameters |
设左像一特征点的64维描述向量为X,右像第i个特征点的64维描述向量为Yi,由
可判断右像第i个特征点即为匹配点。 4 基于核线约束的可靠性匹配完成64维特征向量匹配后,建立核线约束模型,剔除不满足核线约束的点对,提高匹配可靠性。
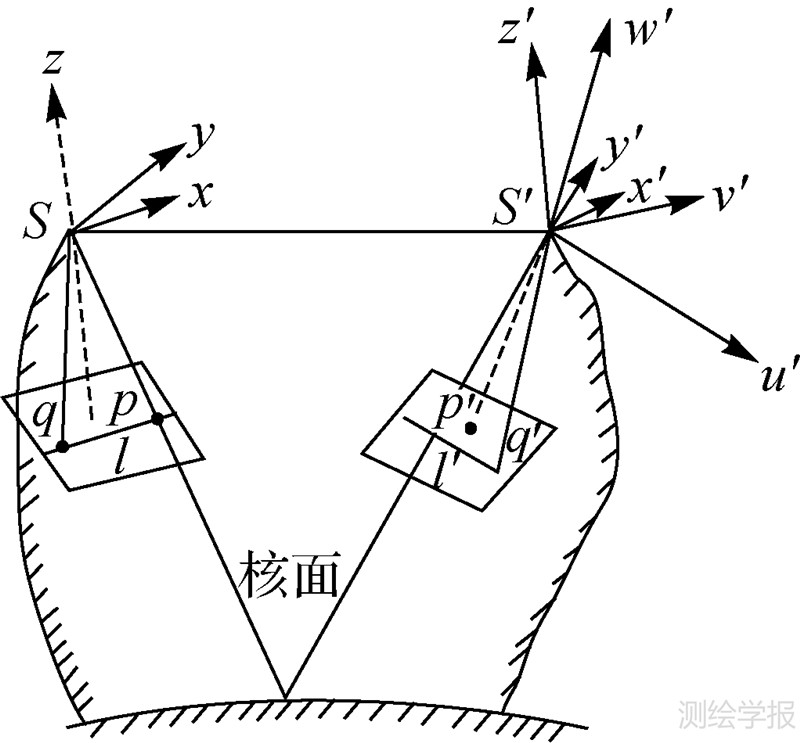
4.1 最优共面模型参数确定由图 4知,左右影像上同名像点满足共面方程展开得[1]
式中,q为“上下视差”;L为待求参数。当已知8对以上同名像点坐标,可根据最小二乘平差解求L参数。
|
| 图 4 核线几何关系 Fig. 4 Relation of epipolar line |
采用随机抽样一致性算法RANSAC(random sample consensus)从匹配点集中迭代搜索匹配点子集,不断修正解算的共面模型(8)中的L参数,计算得到最优共面模型参数,可保证模型整体误差最小。通过试验得出:RANSAC法随机抽取不少于100组同名点对(每组>8对),迭代计算可得到最优模型L参数。
4.2 核线约束检查对于左影像任一特征点p(xp,yp),存在右影像同名像点p′(x′p,y′p),必满足式(7)及式(8)。对于已知x′p,由式(9)计算y′p
由于匹配点对必位于同名核线上,不在同名核线上的点对为误匹配,需要剔除。因此核线约束用于检查发现误匹配,提高匹配的可靠性。
5 试验与分析 5.1 立体影像自动匹配实现(1) 对影像作方向小波变换,得到三尺度低、高频影像,按2.3节进行三尺度影像特征点提取。
(2) 在尺度1 低频影像G1上,给定邻域窗口进行粗匹配。选取满足式(4)并均匀分布的16点对作为粗匹配结果,计算立体像对视差中数。
(3) 在尺度0 低频影像G0上,构造特征点主方向和64维描述向量,进行向量距离匹配。
(4) 计算最优共面模型参数,基于式(9)进行核线约束,剔除误匹配点对。
5.2 试验与结果分析本文采用3种平台获取的立体像对(像对间存在尺度与旋转变化)进行匹配试验。为了说明本文算法的优越性,对试验结果进行人工检查,表 1列出传统基于特征匹配算法及本文算法得到的正确匹配点对数。
| 正确匹配点对数 | ||
| 传统算法 | 本文算法 | |
| 无人机平台立体像对匹配(右像顺时 针旋转15°) | 217 | 415 |
| 地面立体像对匹配(右像逆时针旋 转30°) | 65 | 384 |
| 航空立体像对匹配(右像顺时针旋转120°) | 25 | 420 |
| 无人机平台立体像对匹配(右像缩到 0.6倍) | 44 | 95 |
| 地面立体像对匹配(右像缩到0.6倍) | 19 | 77 |
| 航空立体像对匹配(右像缩到0.6倍) | 7 | 128 |
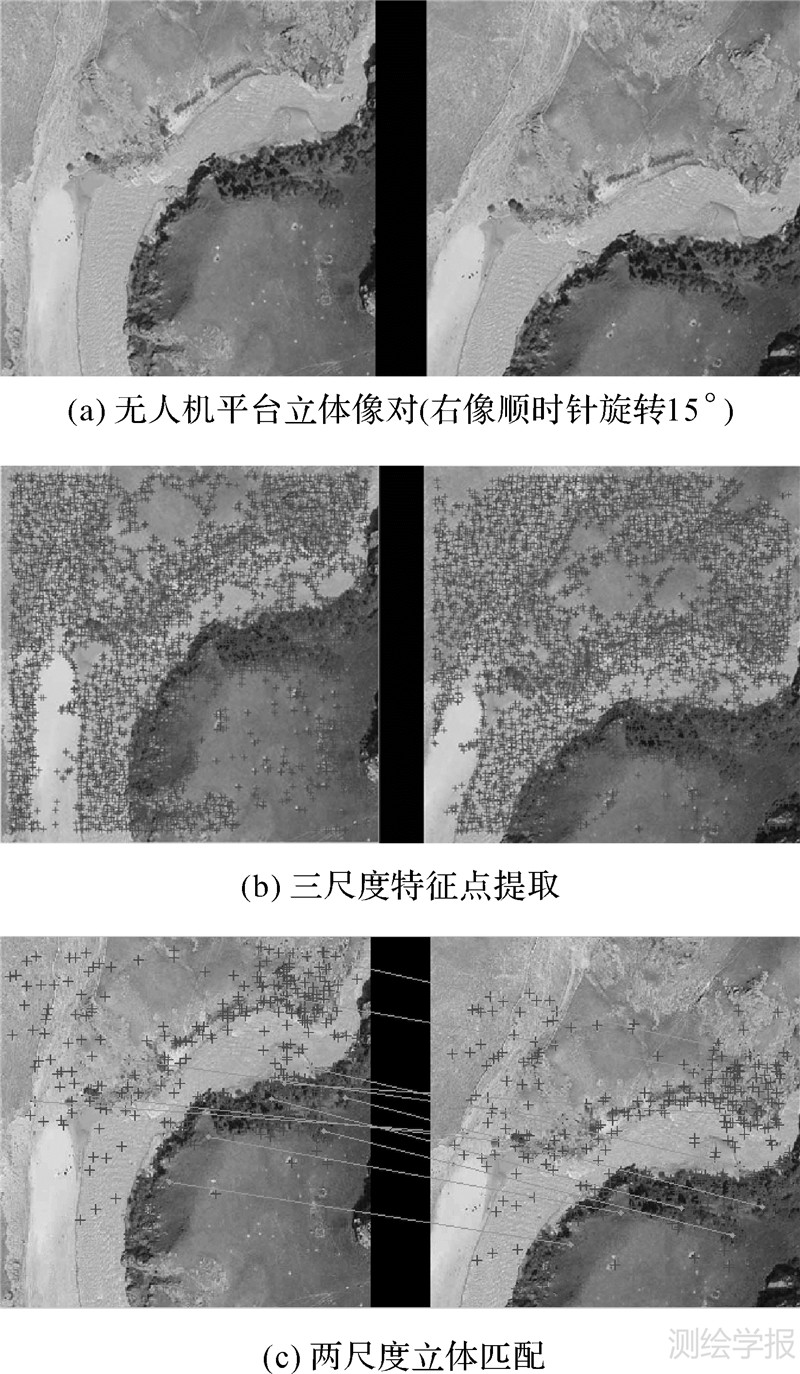
(1) 图 5(a)采用Cannon EOS 400D 数字相机在地面拍摄立体影像,影像尺寸:3888像素×2592像素。对右像逆时针旋转30°;图 6(a)以无人机为遥感平台用Cannon EOS 400D 数字相机拍摄立体影像,相对航高600 m,摄影比例尺1/25 000,对右像顺时针旋转15°;图 7(a)是采用专业DMC面阵相机获取的航空摄影像对,影像尺寸:7680像素×13 824像素,飞行航高800 m,摄影比例尺1/6000,对右像顺时针旋转120°。图 8是将上述3种立体像对的右像缩到原图大小的0.6倍后,与左像的匹配效果。

|
| 图 5 地面影像特征提取与立体匹配 Fig. 5 Feature point extracting and stereo matching by close-range images |
|
| 图 6 无人机平台影像特征提取与立体匹配 Fig. 6 Feature point extracting and stereo matching by unpiloted-aircraft images |

|
| 图 7 航空影像特征提取与立体匹配 Fig. 7 Feature point extracting and stereo matching by airplane images |

|
| 图 8 不同尺度立体影像匹配 Fig. 8 Stereo matching between different scale images |
(2) 图 5(b)、图 6(b)、图 7(b)是在三尺度(尺度2 高频影像、尺度1 高频影像、尺度0 低频影像)下,提取同时满足条件的点作为特征点。3类不同影像对提取效果表明,本算法对于点特征敏感且分布密度均匀。多尺度特征抗辐射强度变化、尺度变化效果明显。
(3) 图 5(c)、图 6(c)、图 7(c)是首先在G1低频影像上,基于(4)式获取均匀分布的16对匹配点,计算影像对的视差中数;然后在G0低频影像上,确定特征点主方向及与主方向有关的64维特征向量,进行向量距离匹配;最后用核线约束剔除误匹配,确保匹配可靠性。为了便于说明,在图 5(c)、图 6(c)、图 7(c)分别表示出10对匹配点。由于立体匹配是在两尺度下完成,其结果具有一定抗尺度变化,基于主方向的64维向量匹配保证了匹配过程的旋转不变性。
(4) 图 8试验结果表明,无论是地面、无人机还是航空平台得到立体像对,其立体匹配尺度不变性效果明显。
(5) 表 1表明,当立体影像间存在尺度与旋转变化时,本文算法匹配获得的正确匹配点对数远多于传统算法,优势明显。
6 讨 论常用立体影像匹配算法,当影像视差不连续、影像间存在明显辐射强度变化,或影像间存在旋转、尺度变化时匹配效果不好。试验结果表明,本文提出基于方向小波多尺度算子、64维特征描述向量、两尺度匹配,可以解决影像尺度和旋转不变性问题。今后需要进一步研究、提高多方向多尺度点特征提取精确性,特别是提高算法对于特殊关键点(如建筑物角点、道路交叉点等)的选择性;另外,进行地面大交向角立体像对匹配时,得到的正确匹配点对较为稀疏,不能满足摄影测量的要求,需要进一步研究改善,同时对城市建筑物特征点匹配的有效性,还需要作深入研究。
| [1] | ZHANG Zuxun. Study on Digital Photo-Grammetry 30 Years[M].Wuhan: Wuhan University Press, 2007.(张祖勋.数字摄影测量研究30年[M].武汉:武汉大学出版社,2007.) |
| [2] | XIONG Xinghua, CHEN Ying,QIAN Zengbo. A Fast, Accurate and Robust Image Matching Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2005,34(1):40-45.(熊兴华,陈鹰,钱曾波. 一种快速、高精度和稳健的影像匹配算法[J].测绘学报,2005,34(1):40-45.) |
| [3] | ZHOU Haifang, TANG Yu, HE Kaitao, et al. An Automatic Global Registration Algorithm Based on Wavelet and Its Parallel Implementation [J]. Acta Automatica Sinica, 2004,30(6):880-889.(周海芳,唐宇,何凯涛,等. 基于小波遥感图像全局配准算法研究及其并行实现[J].自动化学报,2004,30(6):880-889.) |
| [4] | LI Xiaoming. Reaserch in Image Registration Methods[D]. Beijing:Beijing Institute of Technology, 2006. (李晓明.图像配准方法研究[D]. 北京:北京理工大学, 2006.) |
| [5] | MALLAT S. A Wavelet Tour of Signal Processing[M].YANG Lihua, DAI Daoqing, HUANG Wenliang, et al. Translated. Beijing: China Machine Press,2002.(MALLAT S.信号处理的小波导引[M]. 杨力华,戴道清,黄文良,等译.北京:机械工业出版社,2002.) |
| [6] | ANUTA P E. Spatial Registration of Multi-spectral and Multi-temporal Digital Imagery Using Fast Fourier Transform Techniques [J]. IEEE Transactions on Geoscience Electronics, 1970(8):353-368. |
| [7] | CASTRO E D, MORANDI C. Registration of Translated and Rotated Images Using Finite Fourier Transforms[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987,9(5):700-703. |
| [8] | CHEN Q S, DEFRISE M, DECONINCK F. Phase-only Matched Filtering of Fourier-mellin Transforms for Image Registration and Recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994,16(12):1156-1168. |
| [9] | DAVID G L. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision,2004,22(1): 77-85. |
| [10] | BROWN M,LOWE D G. Invariant Features from Interest Point Groups[C]//Proceedings of British Machine Vision Conference. Cardiff: [s.n.], 2002: 656-665. |
| [11] | DENOS M. Automated System for Coarse-to-fine Pyramidal Area Correlation Stereo Matching[J]. Image and Vision Computing,1996, 14(3): 225-236. |
| [12] | HANK P, SONG K W, CHUNG E Y,et al. Stereo Matching Using Genetic Algorithm with Adaptive Chromosomes[J]. Pattern Recognition, 2001, 34(9): 1729-1740. |
| [13] | MALLAT S G. A Theory for Multiresolution Signal Decomposition: the Wavelet Representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1989, 11(7): 674-693. |
| [14] | CANDES E J. Ridgelets: Theory and Application [D]. Stanford: Stanford University, 1998. |
| [15] | DO M N, VETTERLI M. The Contourlet Transform: an Efficient Directional Multi-resolution Image Representation[J]. IEEE Transactions on Image Processing, 2005,14(12):2091-2106. |
| [16] | DONOBO D L. Wedgelets: Nearly Minmax Estimation of Edges[J].The Annals of Statistics, 1999, 27(3): 859-897. |
| [17] | SONKA M, HLAVAC V, BOYLE R. Image Processing, Analysis, and Machine Vision [M]. AI Haizhou, WU Bo,Tanslated. Beijing: Post and Telecom Press, 2003.(SONKA M, HLAVAC V, BOYLE R.图像处理、分析与机器视觉[M]. 艾海舟,武勃,译. 北京:人民邮电出版社,2003.) |
| [18] | TONJES R, GROWE S, BUCKNER J, et al. Knowledge Based Interpretation of Remote Sensing Images Using Semantic Nets[J]. Photogrammetric Engineering & Remote Sensing, 1999, 65(7):811-821. |
| [19] | KRUGER N, PETERS G. ORASSYLL: Object Recognition with Autonomously Learned and Sparse Symbolic Representation Based on Metrically Organizied Local Line Detectors[J]. Computer Vision and Understanding, 2000, 77:48-77. |
| [20] | SZU H H, TELFERN B, KADAMBE S. Neural Network Adaptive Wavelets for Signal Representation and Classification[J]. Optical Engineering, 1998, 31(9):1907-1916. |