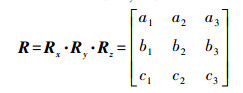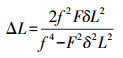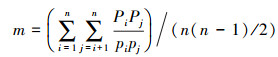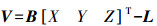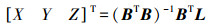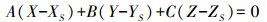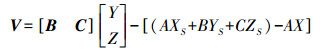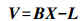2. 东莞中子科学中心, 广东 东莞 523803
2. Dongguan Neutron Science Center, Dongguan 523803, China
为了满足粒子加速器设备高精度安装要求, 准直技术向着多元化的方向发展, 准直对象也逐渐扩展到对丝线等绝对位置的高精度测量。其中, 振动线技术对磁铁磁中心引出标定具有巨大优势, 但是如何将代表磁中心位置的振动线精确引出到磁铁的外基准上, 是需要解决的问题。由于丝线的非接触测量特性, 无法采用高精度的三坐标机、激光跟踪仪等进行接触测量, 而采用传统光学仪器, 如水准仪、工具经纬仪等, 由于受人眼瞄准误差、仪器自身误差等因素影响, 丝线位置测量的精度难以提高。因此, 需要对高精度的丝线绝对位置测量技术进行研究。
目前, 国外加速器准直领域对丝线进行位置测量的方法主要有3种:一维光电式、二维电容式、三维视觉式。在美国斯坦福直线加速器中心SLAC的直线加速器相干光源LCLS四级铁标定中[1-2], 采用一维光电式丝线定位仪确定振动线位置, 其原理为:当光被丝线遮挡时, 则光电传感器接收到的信号产生相应变化, 从而来确定丝线中心相对于光电中心的距离, 最后利用两个垂直放置的丝线定位仪测量出振动线相对于丝线定位仪外部工具球的横向和高程距离。在欧洲核子中心CERN的紧凑型直线对撞机CLIC的DBQ磁铁标定中, 采用二维电容式丝线定位仪确定振动线位置[3-6]。其原理为:当丝线穿过上下左右两对平行电极时, 引起极间介质的介电常数的变化, 从而将丝线位移转换为电容量的变化, 得到丝线相对位移与电容量的线性关系, 最后得到丝线相对于其底板定位基准槽在横向和垂直方向的距离。同样, 在CERN的CLIC概念设计报告中, 提出了一种新的丝线定位技术对引张线的位置进行测量, 从而将设备准直到一条直线上[7-10], 本文称之为三维视觉式丝线定位仪。其原理为:采用2个工业相机, 从两个不同的方向对丝线进行近景成像, 结合预先标定获取的相机位置及参数, 进而得到丝线相对于底板定位基准槽的三维绝对位置。我国即将开工建设的国家重大科技基础设施项目“高能同步辐射光源”HEPS, 其对振动线高精度位置测量精度要求达到10 μm。综上, 本文对采用数字近景摄影测量技术进行丝线三维绝对位置测量的方法进行研究。
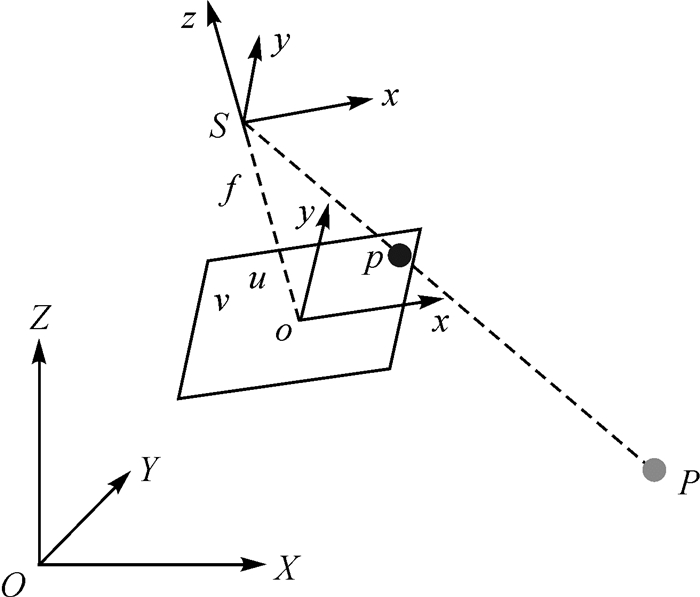
1 数字近景摄影测量原理数字近景工业摄影测量是通过在不同的位置和方向获取同一物体两幅以上的数字图像, 经计算机图像匹配等处理及相关数学计算后得到待测点精确的三维坐标。物方坐标系O-XYZ, 也称为全局坐标系, 用于描述被测目标在物方空间的位置。像空间坐标系S-xyz用于表示像点在像方空间的位置, 原点为光学镜头的投影中心S, z轴和光学镜头的主光轴重合, 垂直于像平面, x轴、y轴分别与像平面坐标系的x轴、y轴平行, So为光学镜头的有效焦距f。如图 1所示。
|
| 图 1 各种坐标系之间的关系 |
首先通过图像传感器的分辨率、尺寸大小, 将像点的像素坐标(u, v)转换成以公制单位表示的像平面坐标(x, y)。假设物方点P在物方坐标系下的坐标为(X, Y, Z), 在像空间坐标系下的坐标为(X', Y', Z'), 其对应的像点p在像空间坐标系中的坐标为(x, y, -f), 投影中心S在物方坐标系下的坐标为(XS, YS, ZS)。根据物方点、投影中心、像点的三点共线条件, 得到物方坐标系与像空间坐标系的转化关系及物方点坐标与像点坐标的关系为
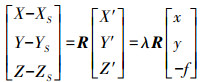 (1)
(1) 式中, R为像空间坐标系向物方坐标系转化的旋转矩阵; λ为比例因子。旋转矩阵的表达可以用绕3个坐标轴的旋转角(εx, εy, εz)来表示
R为正交矩阵, R-1=RT。
相机在实际成像中, 像点在像平面上相对其理论位置存在偏差(Δx, Δy)。将式(1)展开并消去比例因子, 同时顾及像点系统误差的影响, 得到共线方程式[11-12], 如式(2)所示。常用的像点系统误差模型为十参数模型, 除了像主点偏差(x0, y0)和相机有效焦距f外, 还包括镜头形状加工误差引起的径向畸变(k1, k2, k3)、镜头组光心装配误差引起的偏心畸变(p1, p2)、像素的长宽尺度比例因子, 以及像平面x轴和y轴不正交引起的像平面畸变(b1, b1)。采用十参数模型, 则像点的系统误差可以采用下式来表达
 (2)
(2) 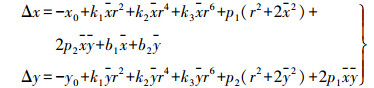 (3)
(3) 式中,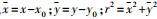
以粒子加速器磁铁预准直中常用的振动线为代表的丝线测量为例, 本项目采用单相机多站位的方法对振动线进行摄影测量。振动线为直径0.1 mm的金属线, 通过丝线夹持机构固定在预准直平台上。为了提高现场测量的适应性, 采用自标定法对相机系统误差进行补偿。首先, 加工建立一个标定平台, 标定平台由底板、标定板及基准座组成, 标定板和基准座固定在底板上, 标定板及基准座的位置关系事先通过高精度的影像仪测得。然后, 在对振动线位置进行测量时, 将标定平台放置在振动线下方, 相机在不同的方位对振动线和标定板同时进行拍摄, 通过标定板提供的高精度控制点坐标, 结合对点和线的亚像素特征提取, 采用自标定光束法平差对相机进行标定及丝线整体求解, 从而得到振动线在标定平台坐标系下的空间位置。最终, 将振动线的位置引出到标定平台的基准座上, 基准座可以放置激光跟踪仪反射球, 从而将振动线引出供激光跟踪仪或三坐标机等进行测量。如图 2所示。

|
| 图 2 摄影测量进行丝线测量 |
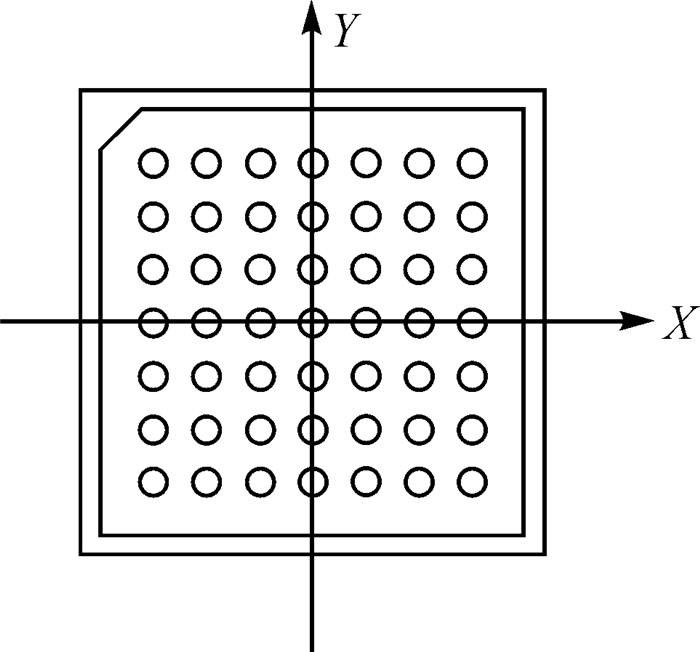
标定板选用Halcon的AFT-MCT-HC50高精度标定板, 其由光学玻璃制成, 具有热膨胀系数小、精度高的优点, 有效尺寸为36 mm×36 mm×2 mm。该标定板由7×7个实心圆组成, 每个圆直径2 mm, 圆心与圆心之间的距离4 mm。另外, 标定板最外层图案为一带斜边的方框, 在点位识别时, 用来对这49个点进行编号。图 3为标定板坐标系, 在该坐标系下, 这49个点的坐标精确已知, 点位精度可达1 μm。
|
| 图 3 标定板坐标系 |
为了能够同时对丝线和标定板进行高质量的成像, 同时满足振动线10 μm的定位精度要求, 对相机参数进行了分析, 包括图像传感器的分辨率、像元尺寸大小、镜头焦距、光圈值等。
(1) 图像传感器的分辨率。系统定位精度10 μm及拍摄视场大小36 mm×36 mm, 假设图像特征提取定位精度能够达到0.5个像素, 则要求图像传感器的分辨率, 即行或列的像素个数最少为0.5×36 mm/10 μm=1800。
(2) 图像传感器的像元尺寸。根据成像系统的缩放系数β=(像元尺寸×所占像元数)/丝线直径, 在β一定的情况下, 像元尺寸越小, 丝线所占的像素越多, 则对于图像特征的精确定位更有利; 另一方面, 在图像特征所占的像元数一定的情况下, 像元尺寸越小, 则缩放系数β越小, 系统成像的景深可以增大。被摄丝线直径为0.1 mm, 同时保证丝线在图像上至少占5个像素, 选择图像传感器的像元尺寸大小为2.2 μm, 此时β=0.11。
(3) 镜头的焦距及光圈值。景深ΔL的近似计算公式为
式中, δ表示容许弥散圆直径; F表示镜头光圈值; f表示镜头焦距; L为物距。可以看出, 景深与光圈值、弥散圆、物距成正比, 与焦距成反比。为了保证合适的景深范围, 将光圈值设为F=22, 弥散圆直径取2个像元大小, 即4.4 μm, 结合系统的缩放系数β=焦距/物距, 焦距为35 mm, 物距为300 mm, 则系统景深可达到14 mm, 满足拍摄要求。
最终, 采用AVT工业相机G-503B, 图像传感器为1/2.5″CMOS, 500万像素, 分辨率2592×1944, 像元大小2.2 μm; 镜头为Computar工业镜头M3520-MPW2, 焦距35 mm, 最大光圈值22。
2.3 丝线测量方法(1) 将标定平台放置在需要测量的丝线下方, 标定板与丝线距离小于5 mm; 同时, 使标定板的X或Y轴与丝线大致平行。在拍摄时, 相机对焦在丝线上, 工作距离约300 mm, 这样保证丝线和圆点都能拍摄清楚。
(2) 将相机固定在支架上, 设置适当的快门, 对丝线和标定板进行拍照, 在拍摄的过程中可以采用光源辅助拍照, 同时要注意相机与丝线之间的方位。
(3) 丝线位置解算, 具体包括:①进行影像特征提取定位, 包括点、线的提取定位; ②相机的外方位元素近似值计算; ③点和线的空间位置近似值计算; ④自标定光3束法求解点、线的空间三维位置。
在空间直线的表达中[13-14], 一般采用点向式来描述, 参数较多, 不方便参与平差计算。由于空间直线的自由度为4, 因此, 为了方便求取空间直线及结果展示, 本文提出采用两个已知平面X1=-12和X2=12, 分别与空间直线相交于两点Q1(-12, Y1, Z1)、Q2(12, Y2, Z2), 则对空间直线的求解转换为求取Q1、Q2点的坐标。
3 参数近似值计算为了进行平差迭代求解, 需要将共线方程线性化, 因此在平差前需要计算各未知参数的初值, 包括外方位元素、待定点坐标、待求直线位置。
3.1 外方位元素近似值计算为了通过单张像片空间后方交会求得单张像片的外方位元素, 即投影中心S的位置(XS, YS, ZS)及外方位角元素(φ, ω, κ), 本文采用基于“以摄影中心为顶点的两根构像光线的像方角应与其物方角相等”原理的角锥体法对相机进行定向[15-16]。
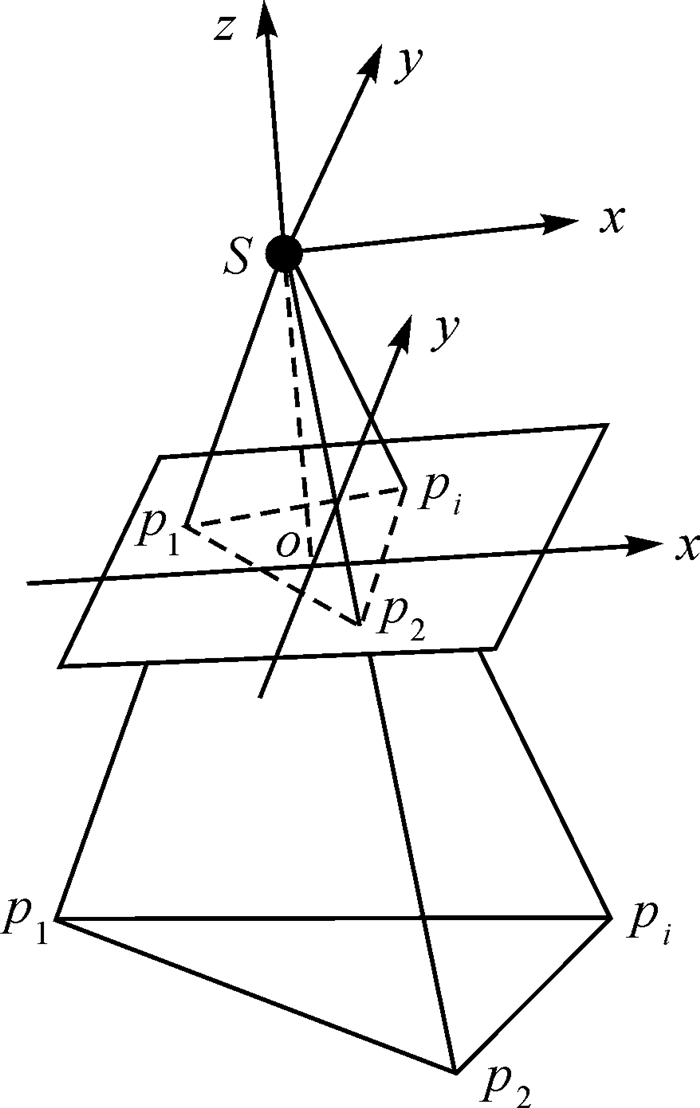
假设物方两个控制点P1、P2通过摄像机得到的相应构像点为p1、p2, 其像面坐标分别为(xp1, yp1)、(xp2, yp2), 如图 4所示。
|
| 图 4 角锥体法定位 |
设投影中心S与像点p1、p2的距离分别为lSp1、lSp2, 由余弦定理可知, 直线Sp1与Sp2的夹角即像方角θp1p2为
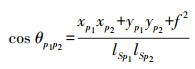 (4)
(4) 式中, 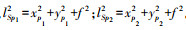
同样设投影中心S与物方点P1、P2的距离分别为LSP1、LSP2, 直线SP1与SP2的夹角即物方角θP1P2为
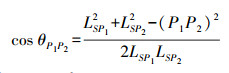 (5)
(5) 式中, 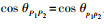
采用角锥体法求取外方位元素, 至少需要4个物方已知点, 如有n个点, 则可列出如式(5)的n(n-1)/2个方程, 把cos θP1P2作为虚拟观测值, 将式(5)按泰勒级数展开线性化, 即可求平差取各摄影中心至各物方点的距离LSPi。在线性化的过程中需要知道摄影中心至各物方点距离的近似值LSPi0, 可以通过物方两点间的距离及相应的像方两点间的距离来计算平均构象比例尺
则摄影中心至各物方点的距离可以近似为LSPi0=mlSPi。此观测值改正数的误差方程为
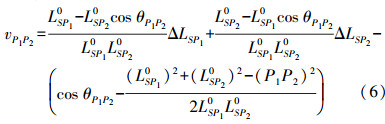 (6)
(6) 式(6)的矩阵形式为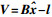
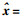
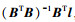
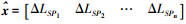
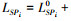
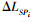
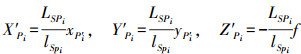 (7)
(7) 对于物方点P1、P2、…、Pn, 得到其在物方坐标系下的坐标(XPi, YPi, ZPi)及其在像空间坐标下的坐标(X'Pi, Y'Pi, Z'Pi)后, 可根据式(1)列出坐标转换方程(式(8)), 通过n个点的坐标最小二乘拟合转换, 具体可以采用基于罗德里格矩阵的方法来实现[17-18], 即可求得相机的外方位元素(投影中心坐标(XS, YS, ZS)和旋转矩阵R)。
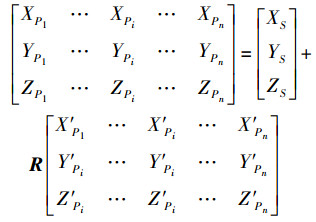 (8)
(8) 得到像片的外方位元素的近似值后, 通过线线前方交会的方法求取物方未知点空间坐标的近似值。由式(1)可得
 (9)
(9) 对于包含待求未知点像点的每一张像片, 均可以列出上述方程, 转换得到
式中,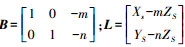
为了求得未知点的近似坐标, 该点至少在两张像片上成像, 当前方交会的像片多于2张时, 则可以较为精确地求解出待定点近似坐标
3.3 待求直线近似位置计算得到像片的外方位元素的近似值后, 通过面面前方交会的方法求得待求直线空间位置的近似值[19-20]。
假设空间直线L在像片上对应的投影直线为l:ax+by+c=0。将共线方程式(2)代入上式, 则可以得到过投影线l及投影中心S的平面Ⅱ
式中,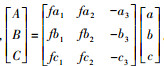
对于包含待求直线图像的每一张像片均可以列出上述方程, 转换得到
为了求得空间直线的近似位置, 该直线至少在两张像片上成像, 通过两个平面方程相交即可求得直线位置。当前方交会的像片多余2张时, 对每一张像片, 令X分别为-12和12, 均可列出2个上述方程, 则可以通过平差求解来较为精确地解算Q1、Q2点的近似坐标。
4 自标定光束法平差采用自标定光束法平差对相机进行标定及空间点、线的求解, 具体分为两步:第一步为整体求解相机的内外方位元素和空间待求点坐标; 第二步为多张像片交会求解空间待求直线的位置。
4.1 内外方位元素求解光束法平差是基于共线条件方程式的, 由式(2)可以看出, 共线条件方程含有三类未知数:物方未知点坐标、摄站外参数和相机内参数。将像点坐标(x, y)视为观测值, 则误差方程可写为
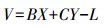 (10)
(10) 式中, V为像点坐标的改正数; X、Y分别为物方未知点坐标、相机内外方位元素的改正数; L为常数项; B、C为系数矩阵。则式(10)法方程为
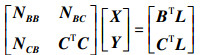 (11)
(11) 式中, 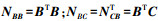
对式(11)采用逐点法化、消元法进行求解。假设有n个物方点, 分别对第i点在所有像片上的相应像点的误差方程进行单独法化、消元, 得到约化法方程式, 将所有的约化法方程式相加, 最终得到只包含相机内、外方位元素改正数Y的约化法方程, 如式(12)所示。对约化法方程求解即可得到各像片的内、外方位元素。
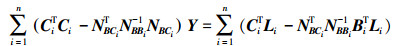 (12)
(12) 利用多张像片的空间前方交会, 逐点计算各待定点的物方坐标。由于已经求解出Y, 因此式(10)可以写为
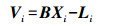 (13)
(13) 对于物方未知点Pi, 将其在m张像片上的所有相应像点列出式(13)方程式, 当此点在两张以上的像片上成像时, 可以用最小二乘平差解算出该点的坐标。对于其他物方未知点的求解按此方法进行。
4.3 待求直线精确求解对于空间待求直线L上的两点Q1(-12, Y1, Z1)及Q2(12, Y2, Z2), 需要求取的未知参数为4个坐标分量(Y1, Z1, Y2, Z2)。将这两点分别代入共线方程式(2), 得到Q1、Q2对应的像点坐标q1(x1, y1)、q2(x2, y2), 即
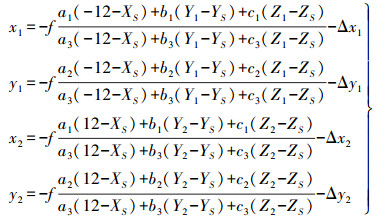 (14)
(14) 通过直线特征提取及定位, 得到空间直线L在像片上对应的投影直线为l:ax+by+c=0。分别求得像点q1、q2到直线l的距离
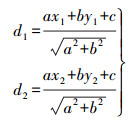 (15)
(15) 将式(14)代入式(15), 然后分别对[Y1 Z1 Y2 Z2]T求偏导进行线性化展开, 得到误差方程
式中, 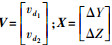
每张像片可以列出一组上述方程, 当有2张像片时, 共有4个方程, 可以求解4个未知坐标分量, 即确定空间直线L。当多于2张像片时, 需要进行最小二乘求解, 使得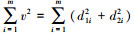
为了验证本文理论及方法的正确性, 同时由于空间直线的精确位置不易获得, 本文采用标定板上两点的连线代替直线进行空间直线求解验证。详细的试验方法为:取标定板上的两点P01和P49的连线作为待求直线L1, 点P02和P48的连线作为待求直线L2; 以P01像点和P49像点的连线作为直线L1的投影线, 以P02像点和P48像点的连线作为直线L2的投影线。以P03—P47作为已知控制点, 计算相机的内、外方位元素, 以所有像片上直线L1的投影线和直线L2的投影线进行整体前方交会求解直线L1和直线L2的位置。具体计算过程如下:
(1) 圆心像素坐标提取。相机在多个位置拍摄标定板, 总共拍摄16张像片。借助Halcon提供的函数库, 利用find_calib_object函数寻找矩形轮廓, 并定位标定板位置; 利用get_calib_data_observ_points函数寻找矩形框中的椭圆并编号, 然后进行亚像素边缘提取, 对满足条件的轮廓进行椭圆拟合; 最终, 得到各个点对应的像素坐标。
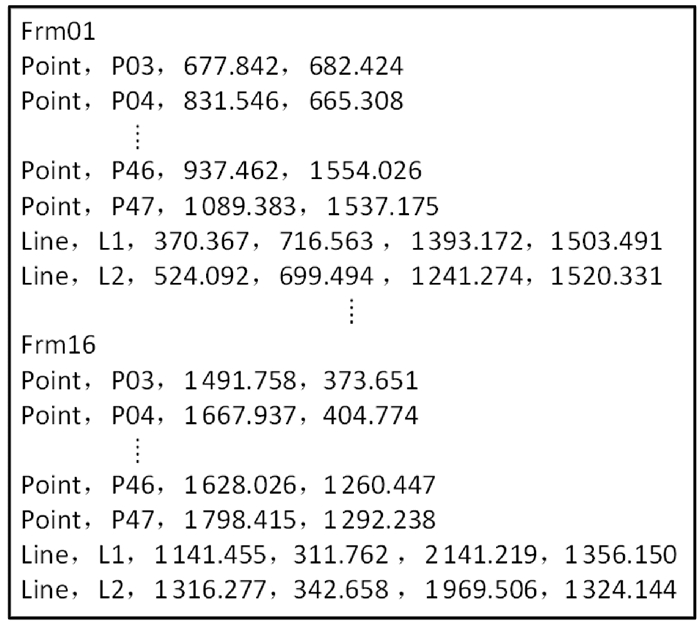
(2) 像素坐标输入。将每张图像中所有的像点及投影线列出形成一个文本文件, 如图 5所示。图 5中像片Frm01列出了点P03—P47的像点坐标, 以及构成投影线L1的两像点坐标P01(370.367, 716.563)、P49(1 393.172, 1 503.491)、构成投影线L2的两像点坐标P02(524.092, 669.494)、P48(1 241.274, 1 520.331)。
|
| 图 5 数据输入格式 |
(3) 自标定光束法平差计算。将上述文本文件输入程序计算后, 得到相机的内参数, 以像素为单位表示: f=17 697.8, x0=990.511, y0=1 340.170, k1=-0.029 387 3, k2=0.005 780 4, k3=-0.000 532 844, p1=-0.007 257 86, p2=-0.018 183 6, b1=0.060 427 9, b2=-0.062 861 4。利用式(15)计算平差后的像点残差RMS=0.045, u、v为原始像点坐标,û 、
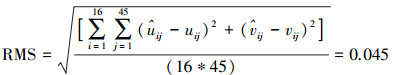 (16)
(16) 待求直线L1由(-12, Y1, Z1)、(12, Y49, Z49)两点来表示, 待求直线L2由(-8, Y2, Z2)、(8, Y48, Z48)两点来表示, 对组成两条直线的4点的坐标分量求解即得到这两条直线的空间位置。将平差得到这4点坐标与理论值进行对比, 差值见表 1。
| mm | |||||
| 空间直线 解算 | 理论 点坐标 | 实测 点坐标 | 误差 | ||
| 直线L1 | X | -12 | -12 | 0 | |
| P01 | Y | 12 | 11.999 6 | -0.000 4 | |
| Z | 0 | 0.003 1 | 0.003 1 | ||
| X | 12 | 12 | 0 | ||
| P49 | Y | -12 | -11.998 9 | 0.001 1 | |
| Z | 0 | 0.002 8 | 0.002 8 | ||
| 直线L2 | X | -8 | -8 | 0 | |
| P02 | Y | 12 | 11.999 1 | -0.000 9 | |
| Z | 0 | 0.002 2 | 0.002 2 | ||
| X | 8 | 8 | 0 | ||
| P48 | Y | -12 | -11.998 8 | 0.001 2 | |
| Z | 0 | 0.002 0 | 0.002 0 | ||
本文对采用摄影测量技术进行丝线空间三维绝对位置高精度测量方法进行了研究, 从拍摄硬件及解算方法上进行了详细论述, 最终, 采用标定板上的两点来模拟代表直线, 通过对标定板的实际拍摄来验证直线测量精度。从表 1可以看出:点位横向Y测量精度比高程方向Z略高, 这与摄站交会角度有关; 同时, 通过实测坐标与理论坐标对比, 点位坐标分量差值最大为3.1 μm, 这表明本文方法的测量精度非常高, 验证了本文方法的正确性。本文的研究及试验为下一步真正的丝线高精度空间绝对位置测量打下了基础。
| [1] |
WOLF Z. A vibrating wire system for quadrupole ducializa-tion[C]//Proceedings of LCLS Technical Note.[S.l.]: SLAC, 2005.
|
| [2] |
LEVASHOV Y M, WOLF Z.Set up and test results for a vibrating wire system for quadrupole fiducialization[C]//Proceedings of LCLS Technical Note.[S.l.]: SLAC, 2006.
|
| [3] |
DURAND M H. Novel method of fiducialisation[C]//Proceedings of IWAA 2014. Beijing: IHEP, 2014.
|
| [4] |
DURAND M H, DUQUENNE M, SANDOMIERSKI J, et al. Drive beam quadrupoles for the CLIC project: a novel method of fiducialisation and a new micrometric adjustment system[C]//Proceedings of IWAA 2014. Beijing: IHEP, 2014.
|
| [5] |
TOUZÉ T. Feasibility of the CLIC metrological reference network[C]//Proceedings of IWAA 2010. DESY, Germany: [s.n.], 2010.
|
| [6] |
DUQUENNE M. Determination of the magnetic axis of a CLIC DB quadrupole using a combination of WPS, CMM and laser tracker measurements[R].[S.l.]: CERN, 2014.
|
| [7] |
BESTMANN P, HERTY A, BENSINGER J, et al. Validation of an optical WPS system[C]//Proceedings of IWAA 2010. DESY: [s.n.], 2010.
|
| [8] |
DANIELS D, HASHEMI K, BENSINGER J. BCAM camera calibration[R].[S.l.]: CERN, 2000.
|
| [9] |
DURAND M H, BESTMANN P, HERTY A, et al. oWPS versus cWPS[C]//Proceedings of IWAA 2012. DESY: [s.n.], 2012.
|
| [10] |
HERTY A. Micron precision calibration methods for alignment sensors in particle accelerators[D]. Nottingham: Nottingham Trent University, 2009.
|
| [11] |
黄桂平. 数字近景工业摄影测量理论、方法与应用[M]. 北京: 科学出版社, 2016.
|
| [12] |
冯其强.数字工业摄影测量技术研究与实践[D].郑州: 解放军信息工程大学, 2010.
|
| [13] |
邱武, 丁明跃, 周华. 基于三维Hough变换的三维超声针状物体检测[J]. 计算机工程与科学, 2009, 31(6): 30-33, 39. DOI:10.3969/j.issn.1007-130X.2009.06.010 |
| [14] |
ROBERTS K. A new representation for a line[C]//Proceedings of CVPR'88. Ann Arbor: IEEE, 1988: 635-640.
|
| [15] |
冯文灏. 近景摄影测量[M]. 武汉: 武汉大学出版社, 2002.
|
| [16] |
邾继贵, 于之靖. 视觉测量原理与方法[M]. 北京: 机械工业出版社, 2011.
|
| [17] |
姚吉利, 韩保民, 杨元喜. 罗德里格矩阵在三维坐标转换严密解算中的应用[J]. 武汉大学学报(信息科学版), 2006, 31(12): 1094-1096, 1119. |
| [18] |
陈林宇. 基于罗德里格矩阵的三维坐标转换方法研究[J]. 地理空间信息, 2018, 16(11): 107-109, 12. DOI:10.3969/j.issn.1672-4623.2018.11.031 |
| [19] |
姜楠.摄影测量计算机视觉在工业测量中的关键技术[D].西安: 西安科技大学, 2008.
|
| [20] |
张永军.基于序列图像的工业钣金件三维重建与视觉检测[D].武汉: 武汉大学, 2002.
|