2. 江苏省地理信息资源开发与利用协同创新中心, 江苏 南京 210023;
3. 南京师范大学地理科学学院, 江苏 南京 210023;
4. 江苏省地理环境演化国家重点实验室培育建设点, 江苏 南京 210023
2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China;
3. School of Geography, Nanjing Normal University, Nanjing 210023, China;
4. Jiangsu Province State Key Laboratory Cultivation Base of Geographical Environment Evolution, Nanjing 210023, China
城市建筑物高度对建筑物容积率、城市三维重建、城市环境等都具有显著的影响[1]。近年来, 随着高分辨率遥感技术的日益发展, 利用高分辨率遥感影像获取建筑物的高度吸引了国内外许多学者的研究。目前的研究方法总体上可分为两类:一是利用高分辨率影像立体像对, 根据空中三角测量原理来计算建筑物高度[2-4], 该方法理论精度较高, 但需要具有一定重叠度的两幅或多幅影像; 二是根据太阳、卫星方位角度、阴影长度与建筑物的空间几何关系来估计建筑物高度[5-8], 该方法应用较多, 计算量少且成本较低, 但是受阴影质量的影响较大, 当遇到建筑物阴影相互遮挡等复杂情况时, 建筑物高度估计的精度很难达到实际应用要求。
针对当前研究方法的不足, 本文根据卫星侧视成像情况下因高差引起的建筑物像点位移与建筑物高度之间的几何关系, 提出基于建筑物侧面轮廓线的高分辨遥感影像建筑物高度估算方法, 利用实际高分辨率遥感影像进行试验验证, 并与基于阴影建筑物高度提取法进行对比, 试验结果表明本文方法可以得到较高精度的建筑物高度估算结果。
1 本文方法原理本文根据卫星侧视成像时因高差引起的建筑物像点位移与建筑物高度的关系, 通过提取影像中的建筑物侧面轮廓线并计算其长度, 从而反算建筑物的高度。本文方法的总体技术路线如图 1所示。
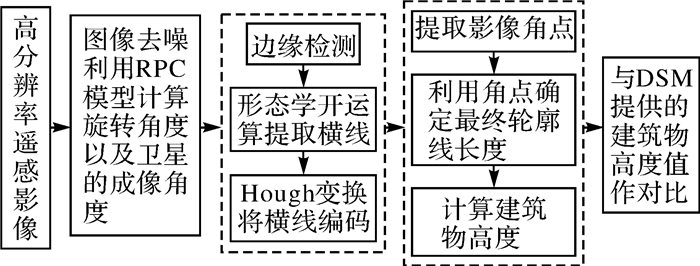
|
| 图 1 本文方法的技术路线 |
本文利用有理函数模型计算像点位移的角度技术流程为:先采用RPC模型的反解形式(见式(1)), 取图像上一点, 坐标为(r0, c0), 初始高程为该地区的平均高程Z0, 经过计算便得到一个虚拟的物点(X0, Y0, Z0), 然后以10 m为间隔取Z0附近7个点; 再利用RPC模型的正解形式(见式(2))求得对应的7个像点, 对这些像点进行函数拟合, 根据相关核线理论, 航天遥感影像的核线在小范围内可看做直线[9-11], 且WorldView系列影像核线具有很好的平行特性[12], 因此这几个像点可以用一条直线进行拟合, 像点位移的方向便是该直线的方向α(α=tan-1k, k为拟合直线的斜率)。
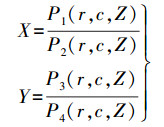 (1)
(1) 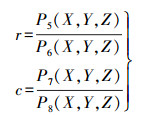 (2)
(2) 式中, (r, c)和(X, Y, Z)分别为经过归一化处理的像点的像方坐标及其对应的物方点坐标; P1, P2, …, P8为有理多项式函数, 函数系数可从卫星影像的RPC文件中获得。
1.2 基于RPC模型的卫星成像角度计算相关研究表明[13], 线阵遥感卫星侧视成像时像移误差公式为
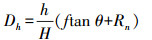 (3)
(3) 式中, Dh为像点位移的大小; h为地面高度; H为卫星轨道高度; f为传感器焦距; Rn为中心像元到第n个成像像元的距离, 若Rn以向外侧CCD方向为正方向, 取正, 若以向内侧CCD方向为负方向, 取负。一般而言, Rn相比ftan θ是一个极小量, 因此在极小范围内Rn可看做常数, 即ΔDh与h正相关, 由于影像中通过使用RPC模型计算得到的7个虚拟像点分别对应着不同的高程h, 不同像点间的距离ΔDh同样与其对应的物点高程之差Δh成正比, 因此可求得卫星侧视成像的角度θ如下
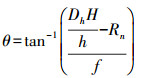 (4)
(4) 利用前面求得的像点位移角度α将图像进行旋转, 使建筑物像点位移的方向沿水平方向。为了获得图像建筑物轮廓线, 首先, 采用Canny[14]边缘检测算法提取建筑物轮廓的二值图像, 然后对二值图像进行形态学闭运算填充小型空洞; 然后, 构建矩形形态学结构元素SE(structure element)对二值图像进行开运算提取图像中的横线, 矩形形态学结构元素的尺寸和方向直接决定检出线状地物的粗细和方向, 由于建筑物轮廓线都是水平的, 因此本文试验主要采用宽度为1、长度一定的结构元素, 长度的选取与建筑物像点位移的距离有关, 像点偏移越严重, 长度越长; 最后, 利用Hough变换, 设置角度阈值为90°检测图像中的横线, 并将横线编码, 从而得到建筑物的轮廓线。
1.4 结合角点约束与几何规则进行横线精简为了使横线的长度更好地契合建筑物的侧面轮廓线, 以及排除路面线等误检横线, 本文首先利用FAST[15]算子进行角点检测, 然后为了使所提取的横线长度更加准确, 本文按照几何形态规则进行横线合并。假设横线的左右两端坐标为(lxl, y)、(lxr, y), 则横线的合并规则如图 2所示。
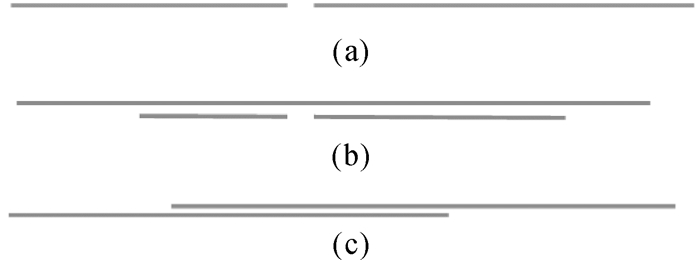
|
| 图 2 横线合并规则 |
规则1:横线“头尾”相距很近, 横线坐标y相近:l2xr-l1xl≤t1, y1-y2≤t2; 规则2:横线包含:l1xl≤l2xl, l1xr≥l2xr, y1-y2≤t2; 规则3:横线“头头”相距很近且坐标y相近:l1xl-l2xl≤t1, y1-y2≤t2。
其中, t1、t2分别为直线坐标x、y距离阈值。横线经过合并之后, 寻找距离端点处最近的角点, 如果提取的横线不能正确契合建筑物的侧面轮廓线, 无论是“超出”或是“过短”的情况, 都可以利用与之一端最近的角点进行约束, 从而对轮廓线的长度进行修正。同样, 如果同一建筑物有多条横线, 则取修正后最长的横线为建筑物侧面轮廓线的长度。
1.5 基于建筑物轮廓线的建筑物高度计算建筑物轮廓线的长度可以很好地表示建筑物在卫星一定侧视成像角度下相对于地面的像点位移长度D'h, 而此位移又与建筑物高度有密切关系。因此, 建筑物的高度h'可利用下式求得
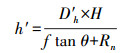 (5)
(5) 式中, f为传感器焦距; H为卫星轨道高度; Rn为中心像元到第n个成像像元的距离; θ为卫星侧视成像的角度。
2 试验与结果分析为了验证本文算法具有比阴影法更好的适用性及准确性, 在Windows 10环境下, 采用Visual C#.NET 2013程序设计语言结合Emgu CV函数库对本文算法进行编程实现, 并采用两组不同地区的遥感影像数据进行对比试验。两组数据都是WorldView-3卫星4波段多光谱影像, 分辨率为1.24 m, 单波段全色影像分辨率为0.31 m及0.5 m的DSM数据(用作建筑物真值作为比对)。多光谱影像与全色影像融合之后试验影像如图 3所示。其中, 影像(a)位于巴西里约热内卢, 尺寸为1302×1086像素, 该影像中建筑物的阴影相互遮挡, 无法有效提取出建筑物阴影, 因此无法使用阴影法进行高度估算; 影像(b)位于利比亚地区, 尺寸为1629×1606像素, 该影像可以很好地提取阴影的长度。

|
| 图 3 试验用的高分辨率遥感影像数据 |
在求出旋转角度α将影像进行旋转之后, 为了更好地进行建筑物轮廓线的提取, 本文将原图像经过双边滤波之后设置Canny算子高低阈值为200进行轮廓提取, 随后进行形态学闭运算, 填充轮廓小空洞, 使轮廓具有更好的连贯性。在进行建筑物的横线提取时, 形态学结构元素的构造对最终的试验结果至关重要[16], 因此试验采用长度为15个像素的矩形结构元素对经过处理后的图像进行开运算, 使用合并精简规则处理之后, 最终的结果如图 4所示。最后设置FAST角点检测器的阈值为60提取图像的角点信息, 以此修正横线的距离, 从而最终确定建筑物侧面轮廓线的长度。

|
| 图 4 不同地区影像建筑物侧面轮廓线提取结果 |
本次试验每组数据各随机选取了15座建筑物, 其真实高度数值从DSM数据上获取。在求得卫星成像角度θ之后, 利用建筑物侧面轮廓线的长度反算建筑物高度, 并与其真值进行绝对误差和相对误差的计算。里约地区试验影像的建筑物高度提取结果见表 1; 对于利比亚地区的试验影像, 利用本文方法和文献[17]中阴影法的建筑物高度提取对比试验结果如图 5所示。
| 楼号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 真值/m | 90.51 | 17.34 | 24.53 | 47.75 | 17.14 | 24.47 | 38.55 | 27.43 | 27.84 | 25.86 | 31.54 | 27.92 | 14.52 | 27.42 | 44.53 |
| 计算值/m | 92.22 | 16.17 | 24.56 | 44.32 | 16.77 | 23.72 | 35.95 | 27.57 | 27.57 | 25.77 | 32.36 | 28.77 | 13.78 | 25.29 | 41.35 |
| 绝对误差/m | 1.71 | 1.17 | 0.03 | 3.43 | 0.37 | 0.75 | 2.6 | 0.14 | 0.27 | 0.09 | 0.82 | 0.85 | 0.74 | 2.13 | 3.18 |
| 相对误差/(%) | 1.89 | 6.75 | 0.12 | 7.18 | 2.16 | 3.06 | 6.74 | 0.51 | 0.97 | 0.35 | 2.60 | 3.04 | 5.09 | 7.77 | 7.14 |
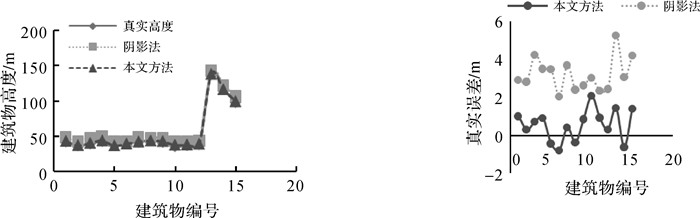
|
| 图 5 基于不同方法的建筑物高度提取的对比试验结果 |
根据试验结果, 里约地区影像建筑物计算结果绝对误差的范围为0.03~3.43 m, 相对误差范围为0.12%~7.77%, 平均误差为0.74 m。而在利比亚影像的试验结果中, 本文方法的建筑物高度估算绝对误差为0.29~2.06 m, 相对误差为0.52%~5.37%;阴影法的绝对误差为2.06~5.26 m, 相对误差为2.63%~10.4%。因此, 本文方法的建筑物高度估算精度明显优于阴影法。
另外, 本文方法的误差大小与建筑物底部被遮掩的情况有关。如果建筑物靠近地面的部分被植物遮挡或处于混合像元, 则本文方法进行建筑物高度测算误差相对较大。但是, 在一定误差允许的范围内, 利用本文方法计算的建筑物高度的精度仍然较高, 有些甚至可以达到分米级, 达到甚至超过了利用阴影法计算建筑物高度的精度。
3 结语本文提出了一种基于建筑物侧面轮廓线的高分辨率影像建筑物高度计算的新方法, 相对于已有的利用阴影求算建筑物高度的方法, 本文方法只需要解算像点位移的方向, 以及卫星侧视成像的角度(在此角度已知的情况下计算量会更少); 而且, 本文方法还可以应用于阴影混淆相互遮挡、卫星夜间成像等阴影法无法应用的情况。通过使用实际遥感影像的试验结果分析, 本文提出的方法比基于阴影的建筑物高度估算方法的精度更高, 且具有更广泛的适应性。但是, 面对建筑物过于密集、建筑物侧面轮廓相互遮挡等复杂情况, 本文方法还存在一定的不足。在未来的研究工作中, 还需要考虑以上更加复杂的情况, 以提高本文方法的适用性。
| [1] |
霍少峰, 顾行发, 占玉林, 等. 资源三号卫星前视影像的建筑物高度提取[J]. 测绘科学, 2017, 42(2): 147-153. |
| [2] |
卓莉, 黄信锐, 王芳, 等. 基于高空间分辨率与立体像对遥感数据的建筑物三维信息提取[J]. 遥感技术与应用, 2013, 28(6): 1062-68. |
| [3] |
陈爱军, 徐光佑, 史元春. 基于城市航空立体像对的全自动3维建筑物建模[J]. 测绘学报, 2002, 31(1): 54-59. DOI:10.3321/j.issn:1001-1595.2002.01.011 |
| [4] |
王伟玺, 宋伟东, 刘艳春. 广义立体像对三维重建模型精度分析[J]. 测绘科学, 2010, 35(4): 31-33. |
| [5] |
刘小洲, 周石琳, 李智勇. 高分辨率遥感图像中建筑物阴影的提取[J]. 计算机仿真, 2008, 25(8): 197-200. DOI:10.3969/j.issn.1006-9348.2008.08.051 |
| [6] |
石义方, 汪小钦, 孙振海, 等. 基于阴影的资源三号卫星数据城市建筑物高度估算[J]. 地球信息科学学报, 2015, 42(13): 236-243. |
| [7] |
王京卫, 郭秋英, 郑国强. 基于单张遥感影像的城市建筑物高度提取研究[J]. 测绘通报, 2012(4): 15-17. |
| [8] |
田峰, 陈冬花, 黄新利, 等. 基于形态学阴影指数的高分二号影像建筑物高度估计[J]. 遥感技术与应用, 2017, 32(5): 844-850. |
| [9] |
张永生, 巩丹超, 刘军. 高分辨率遥感卫星应用:成像模型、处理算法及应用技术[M]. 2版. 北京: 科学出版社, 2014.
|
| [10] |
张永军, 丁亚洲. 基于有理多项式系数的线阵卫星近似核线影像的生成[J]. 武汉大学学报(信息科学版), 2009, 34(9): 1068-1071. |
| [11] |
WANG M, HU F, LI J. Epipolar resampling of linear pushbroom satellite imagery by a new epipolarity model[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(3): 347-355. DOI:10.1016/j.isprsjprs.2011.01.002 |
| [12] |
曹彬才, 邱振戈, 朱述龙, 等. 利用线阵卫星立体像对的平行特性生成核线影像[J]. 测绘通报, 2017(1): 43-47. |
| [13] |
战鹰, 史良树, 王金强, 等. 卫星侧视成像引起的像点位移误差计算方法[J]. 河南理工大学学报(自然科学版), 2015, 34(3): 370-373. |
| [14] |
CANNY J. A computational approach to edge detection[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1986, 8(6): 679-698. |
| [15] |
ROSTEN E, PORTER R, DRUMMOND T. Faster and better: a machine learning approach to corner detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(1): 105-119. DOI:10.1109/TPAMI.2008.275 |
| [16] |
顾徐博君, 虞思逸, 金叶蒙, 等. 基于数学形态学和Hough变换的复杂形态线状地物提取方法[J]. 遥感技术与应用, 2014, 29(4): 689-694. |
| [17] |
胡云锋, 张千力. 结合形态学和光谱特征参数的建筑物阴影提取及其高度估算[J]. 测绘通报, 2018(6): 22-26. |



