2. 地球空间信息技术协同创新中心, 湖北 武汉 430079;
3. 中南大学地球科学与信息物理学院, 湖南 长沙 410083
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China;
3. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China
超高建筑在运营载荷、强风等外界因素影响下将发生特定频率的振动变形及缓慢的似静态变形[1-2]。对超高建筑动态特性进行监测,在验证其结构设计参数、评估其安全运营能力等方面具有重要意义[3-4]。GNSS技术因其具有无需通视,可直接获取三维位移等优点,已经成为高楼风振响应监测的重要手段之一[5]。高楼在高频段的振动信号微弱,由于受到GNSS接收机高频噪声的影响,很难从强噪声背景下的观测信号中提取高楼的弱振动信号[6-7]。目前,学者已经提出了一些数据滤波方法来提取高楼的振动信号,并取得了较好的信噪分离效果[8-9]。加速度计可以直接获取高楼的振动加速度数据,具有采样率高、精度高等优点,但是加速度数据通过积分会导致误差积累,且容易产生零漂,无法实现对高楼低频似静态位移的监测[10]。通过融合GNSS和加速度计数据,可以发挥两者的优势。目前,一些学者在GNSS和加速度计融合方面开展了研究,并在工程、地学等应用领域取得了较好效果[10-12]。
在桥梁,超高建筑等大型结构健康监测领域,一些监测对象同时安装了GNSS接收机和加速度计,虽然取得了一定的监测效果,但是一般都是针对单一GNSS数据或加速度数据进行分析的[9]。为了充分发挥两种传感器的互补优势,本文利用多速率Kalman滤波和RTS(Rauch Tung Striebel)平滑方法,对超高建筑GNSS和加速度计监测数据进行融合处理,并对高楼动态特性进行分析。
1 基于RTS平滑的多速率Kalman滤波Kalman滤波是一个在时间域上不断预测、修正的递推过程,被广泛地应用于动态数据处理[13-14]。在超高建筑动态监测中,加速度计的采样率往往会比GNSS采样率高。融合GNSS数据和加速度计数据需要将位移作为观测量,加速度作为控制量,采用多速率Kalman滤波。
利用多速率Kalman滤波方程融合位移和加速度数据的状态方程式为
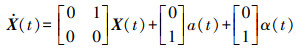 (1)
(1) 式中,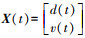
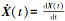
将位移作为观测值,建立Kalman观测方程为
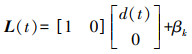 (2)
(2) 式中,βk表示位移观测噪声,β~0, r, r为位移方差。
式(1)和式(2)的离散形式可表示为
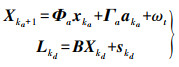 (3)
(3) 式中,aka表示加速度观测值;Lkd表示位移观测值;其状态噪声协方差为Qa和观测噪声协方差为Rd。令加速度采样时间间隔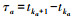
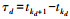
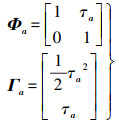 (4)
(4) 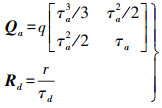 (5)
(5) 融合位移和加速度数据的多速率Kalman滤波流程如图 1所示,具体步骤如下:

|
| 图 1 基于RTS平滑的多速率Kalman滤波流程 |
(1) 初始化
 (6)
(6) (2) 基于加速度数据的预测更新
状态预测公式为
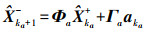 (7)
(7) 状态协方差矩阵预测公式为
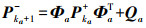 (8)
(8) (3) 当进行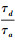
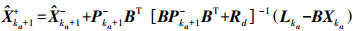 (9)
(9) 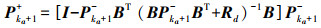 (10)
(10) RTS平滑是一种固定区间最优平滑算法,经过多速率Kalman滤波之后,通过RTS平滑,位移估计精度可以得到大幅度提高[15]。RTS平滑公式为
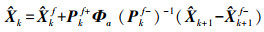 (11)
(11) 式中,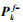
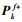
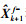
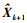
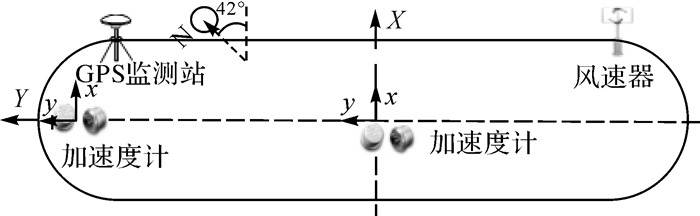
为研究超高建筑在风载荷情况下的动力特性及评估其结构健康状况,某研究机构对一超高建筑进行了长时间的风载动态变形监测。该建筑共68层,高度约为260 m,外形呈长方形,长宽比例为4:1。建筑X方向方位为北偏西42°。监测系统的数据采集设备包括2台GNSS接收机、4个加速度计、1个风速计。其中,2台GNSS接收机组成基线用来监测大厦的风致动态变形,监测站和参考站之间的距离约为0.84 km。4个加速度器用来监测大厦风致振动加速度,它们分两组分别安装在大厦顶层的边翼和中心。GNSS采样率设置为10 Hz,加速度计设置为20 Hz,仪器安置如图 2所示。
|
| 图 2 大厦楼顶平面与传感器布置 |
本文对高楼侧翼1 h的GNSS数据和加速度监测数据进行了分析。加速度计获取的振动加速度时间序列如图 3所示。在图 2所示的坐标系下,GNSS监测的位移时间序列如图 4(a)、图 5(a)所示。在台风的影响下,高楼主轴x方向的振动加速度振幅明显强于y方向。高楼在主轴x方向位移较大,存在明显的变形趋势。主轴y方向的变形位移较小,趋于零值附近波动。监测结果表明,由于受到高楼形状的影响,高楼在主轴x方向上对风载更加敏感。
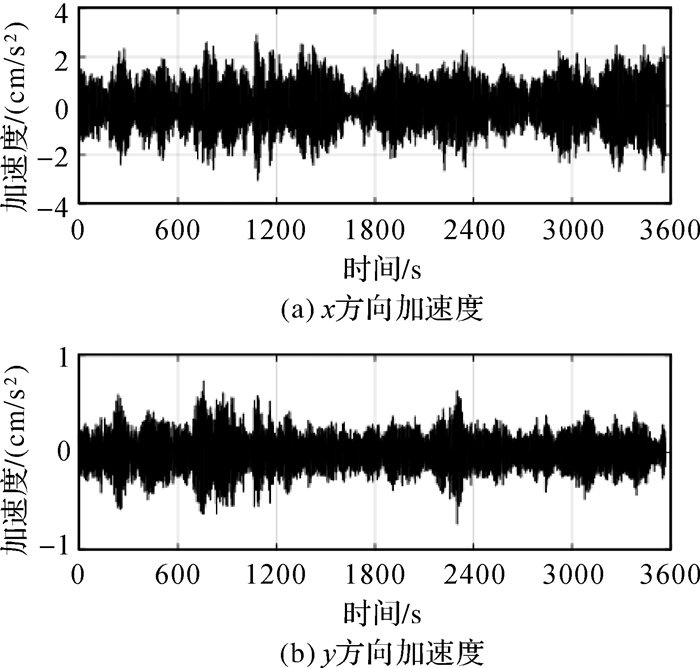
|
| 图 3 加速度计原始时间序列 |

|
| 图 4 x方向原始位移和融合位移时间序列 |
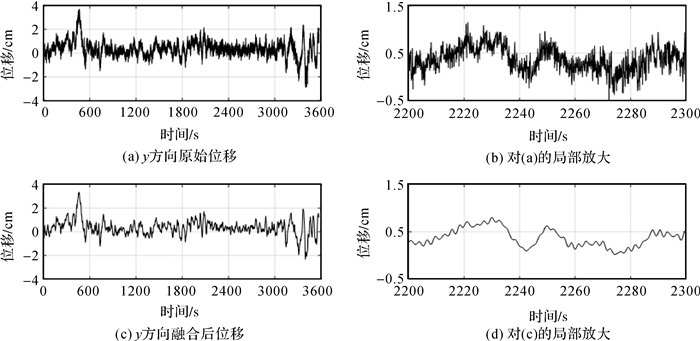
|
| 图 5 y方向原始位移和融合位移时间序列 |
将GNSS和加速度计数据作为输入量,进行多速率Kalman滤波,并对滤波后的数据进行RTS平滑处理,结果如图 4(c)、图 5(c)所示。融合之后的位移数据采样率为20 Hz。将原始位移数据和融合后位移数据进行对比分析可以发现,二者的整体变化趋势一致,融合位移保留了高楼低频变形信息。融合后的位移更加平滑,尤其是在振动不敏感的y方向,由于受接收机噪声的影响,高楼微弱振动信号已经被淹没。数据融合之后,高频噪声得到了很好的抑制,从而可以监测到高楼微弱的振动位移。
为了研究高楼的动态特性,需要将时间域数据转换到频率域。基于快速傅里叶变换对图 4和图 5位移数据进行频谱分析,结果如图 6所示。由于高楼似静态变形和多路径的影响,位移数据在低频部分表现出较高的功率谱密度。高楼的前3个主模态振动频率分别为0.21、0.34、0.44 Hz。融合后的位移时间序列和原始位移时间序列相比,功率谱密度更加平滑,在高频部分功率谱密度较低,融合后的位移时间序列受白噪声的影响较小。
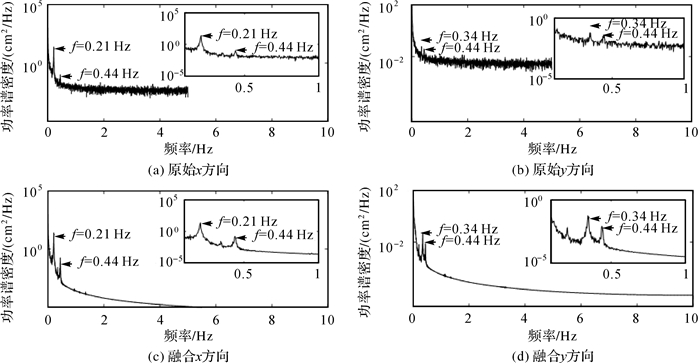
|
| 图 6 位移时间序列频谱分析结果 |
将融合位移序列对时间进行两次差分处理转化为加速度。图 7(a)、(b)是加速度计原始监测数据的频谱分析结果。图 7(c)、(d)是融合位移转化的加速度频谱分析结果。结果表明,加速度计和GNSS识别的前3个振动频率是一致的。与GNSS技术相比,加速度计能够监测出更多的振动频率,这主要是因为加速度计的精度更高,对高楼的振动信号更加敏感。融合位移转换的加速度可有效识别高楼低频和高频振动频率。该方法在消除GNSS高频噪声的同时,依然保留了高频振动信息。

|
| 图 7 加速度时间序列频谱分析结果 |
小波分析是一种在全频段内对信号进行多分辨率分解的方法,具有很好的时频局部化优点。因其具有带通滤波的特性,常被用于超高建筑振动信号提取[8-9]。本文采用小波分析对高楼x方向和y方向的原始位移和融合后的位移进行振动信号提取,将提取的振动位移进行两次时间差分转化为加速度,同时对侧翼x方向和y方向加速度计数据进行振动提取。结果如图 8所示。在高楼x方向谐振振幅较大,对原始位移信号进行小波分析,提取的高楼振动位移转化的加速度和提取的加速度计振动信号具有很好的一致性。但是在y方向上,由于高楼谐振振幅较小,振动信号信噪比较低,利用原始数据提取的振动位移转换的加速度和提取的加速计振动信号相比,存在一定的偏差。利用融合后的位移数据提取的振动信号,无论是在x方向还是y方向上都与提取的加速度计振动信号有较好的吻合。结果表明,融合GNSS和加速度计数据,可以减弱高频噪声的影响,提高对超高建筑微弱振动信号的监测能力。
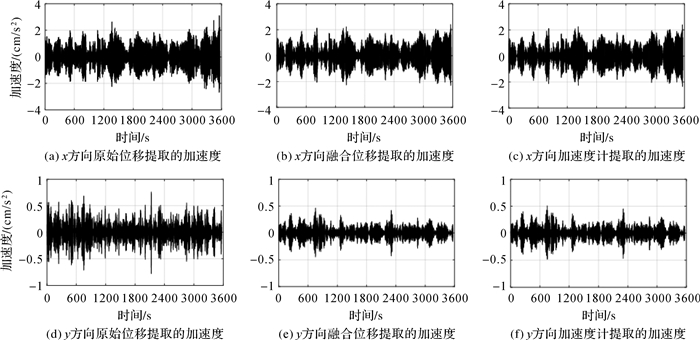
|
| 图 8 提取的高楼振动加速度 |
GNSS和加速度计已成为超高建筑动态监测的重要技术手段,对这两种传感器监测数据进行融合处理,可充分发挥两者的互补优势。针对GNSS对超高建筑微弱振动及高频振动信息不敏感的问题和加速度计无法监测低频变形的缺陷,本文利用多速率Kalman滤波和RTS平滑方法,融合超高建筑的GNSS和加速度计监测数据,并对高楼的振动特性进行了分析。数值结果表明,该方法可以提高位移数据的采样率,有效识别高楼的低频和高频振动频率。在保留高楼低频变形信息的同时,削弱了GNSS的高频噪声,提高了对超高建筑振动微变形的监测能力。该方法在高楼动态监测中具有良好的应用价值。
| [1] |
YI Z H, KUANG C L, WANG Y R, et al. Combination of high-and low-rate GPS receivers for monitoring wind-induced response of tall buildings[J]. Sensors, 2018, 18(12): 4100. DOI:10.3390/s18124100 |
| [2] |
匡翠林, 张晋升, 曾凡河, 等. GPS监测高层建筑在台风载荷下的动态响应特征[J]. 大地测量与地球动力学, 2012, 32(6): 139-143. |
| [3] |
林巍, 黄铭枫, 郭中秀, 等. 台风下香港K11大楼风振响应实测及分析[J]. 深圳大学学报(理工版), 2012, 29(1): 45-50. |
| [4] |
GÍRSKI P. Dynamic characteristic of tall industrial chimney estimated from GPS measurement and frequency domain decomposition[J]. Engineering Structures, 2017, 148: 277-292. DOI:10.1016/j.engstruct.2017.06.066 |
| [5] |
KALOOP M R, ELBELTAGI E, HU J W, et al. Recent advances of structures monitoring and evaluation using GPS-time series monitoring systems:a review[J]. International Journal of Geo-Information, 2017, 6(12): 382. DOI:10.3390/ijgi6120382 |
| [6] |
戴吾蛟. GPS精密动态变形监测的数据处理理论与方法研究[D].长沙: 中南大学, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10533-2007197868.htm
|
| [7] |
YI T H, LI H N, GU M. Experimental assessment of high-rate GPS receivers for deformation monitoring of bridge[J]. Measurement, 2013, 46(1): 420-432. DOI:10.1016/j.measurement.2012.07.018 |
| [8] |
黄声享, 刘经南, 柳响林. 小波分析在高层建筑动态监测中的应用[J]. 测绘学报, 2003, 32(2): 153-157. DOI:10.3321/j.issn:1001-1595.2003.02.012 |
| [9] |
匡翠林, 戴吾蛟. GPS监测高层建筑风致振动变形及小波应用[J]. 武汉大学学报(信息科学版), 2010, 35(9): 1024-1028. |
| [10] |
戴吾蛟, 伍锡锈, 罗飞雪. 高楼振动监测中的GPS与加速度计集成方法研究[J]. 振动与冲击, 2011, 30(7): 223-226, 249. DOI:10.3969/j.issn.1000-3835.2011.07.043 |
| [11] |
于先文, 薛红琳. 基于GPS/加速度计组合的桥梁振动监测方法[J]. 东南大学学报(自然科学版), 2013, 43(S2): 329-333. |
| [12] |
CHAN W S, XU Y L, DING X L, et al. An integrated GPS-accelerometer data processing technique for structural deformation monitoring[J]. Journal of Geodesy, 2006, 80(12): 705-719. DOI:10.1007/s00190-006-0092-2 |
| [13] |
林旭, 罗志才. 位移和加速度融合的自适应多速率Kalman滤波方法[J]. 地球物理学报, 2016, 59(5): 1608-1615. |
| [14] |
SMYTH A, WU M. Multi-rate Kalman filtering for the data fusion of displacement and acceleration response measurements in dynamic system monitoring[J]. Mechanical Systems and Signal Processing, 2007, 21(2): 706-723. DOI:10.1016/j.ymssp.2006.03.005 |
| [15] |
BOCK Y, MELGAR D, CROWELL B W. Real-time strong-motion broadband displacements from collocated GPS and accelerometers[J]. Science, 2011, 336(6082): 707-710. |


