2. 甘肃省地理国情监测工程实验室, 甘肃 兰州 730070;
3. 兰州精准地形沙盘模型智能制造有限公司, 甘肃 兰州 730020;
4. 68029部队博士后科研工作站, 甘肃 兰州 730020
2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Gansu Province, Lanzhou 730070, China;
3. Lanzhou Precision Sand Table Model Intelligent Manufacturing Co., Ltd., Lanzhou 730020, China;
4. Post-Doctor Research Center of 68029 Troops, Lanzhou 730020, China
2014年8月19日,高分二号(GF-2)卫星的成功发射实现了亚米级空间分辨率、多光谱综合光学遥感数据的获取,成为我国遥感事业的里程碑。充分利用高分辨率遥感影像及时、精确获取水体信息有利于水利规划、水资源保护与监测、洪涝灾害应急救助等。目前常用的水体提取方法主要有单波段阈值法、归一化差分植被指数法(NDVI)及各种水体提取指数法等,上述方法在中、低分辨率遥感影像上具有很好的适用性。
在高分影像研究中,文献[1]以GF-2影像为数据源,采用基于面向对象分析技术,提出了一种选取最佳分割尺度和特征规则的方法,提取了杭嘉湖水网平原的水体。文献[2]基于GF-1卫星影像对比分析了水体指数模型法、单波段阈值法、谱间关系法在河流水域面积提取上的差异,结果显示水体指数阈值法对大型的河流、湖泊提取效果较好。文献[3]利用GF-2卫星融合影像很好地识别了城镇区域内宽度较窄的河道岸线,并判定水面浮萍的存在。文献[4]提出了基于LBV变换的水体提取方法。首先通过对GF-2影像的LBV变换及其归一化,得到了物理意义明确的L、B、V变换分量;然后利用这3个分量计算特征分量BL、BV,构建了完整的水体提取方案。文献[5]通过分形网络进化算法实现影像分割并借助ESP尺度分割工具选取特定地物的最优分割尺度,随后使用基于规则的面向对象方法实现了水体信息的精确提取。文献[6]基于GF-1、GF-2遥感影像提出了一种基于面向对象和人工蜂群的地表水体提取方法。该方法首先对遥感图像进行分割以获取分割对象的光谱、比率、几何形状等统计特征,然后借助人工蜂群算法在解决复杂问题最优化方面的优势,选取水体同阴影二值分类的几何平均正确率作为算法的适应度函数,最终获取地表水体的最优化提取规则。
本文以GF-2影像为数据源,针对GF-2影像波段的特点,利用不同的水体提取指数模型对两个不同的研究区进行水体试验,分析比较不同地区、不同水体提取模型及阈值对水体提取精度和稳定性的影响,为后续利用GF-2影像进行水体提取试验提供参考和依据。
1 研究区概况与数据源 1.1 研究区概况临夏回族自治州位于甘肃省中部西南面,黄河上游,北与兰州接壤,东临洮河与定西相望, 西倚积石山与青海省海东地区毗邻,南靠太子山与甘南藏族自治州搭界。临夏回族自治州是黄河上游重要的水源补给区,州内河流都属黄河水系。黄河流经临夏州境内约103 km,一级支流有洮河、大夏河、湟水河等,有黄河三级以上支流30多条[7]。文中选取两个不同区域的水体,研究区1为城市区域水体,研究区2为山区水体,如图 1所示。

|
| 图 1 研究区影像 |
本文采用的GF-2数据源为2017年11月11日获取的PMS2、LEVEL1A级别影像,影像无云覆盖且成像质量良好。在ENVI 5.3软件中对GF-2影像进行预处理,主要包括辐射定标、FLAASH大气校正、正射校正及图像融合。其中图像融合采用NNDiffuse Pan Sharpening方式,该方式获取的融合结果对于色彩、纹理和光谱信息,能够得到很好的保留[8-11]。
2 水体提取方法与结果 2.1 水体提取指数模型(1) 单波段阈值法(NIR)。在近红外波段水体与其他地物的灰度值差距最大,使水体能够与非水体信息较好地分离。因此,单波段阈值法主要利用对水陆界线反映较好的近红外波段,根据影像的灰度特征经过数据采样确定阈值进行水体的提取。GF-2影像提取模型如下
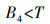 (1)
(1) 式中,B4表示近红外波段的灰度值;T为水体提取的灰度阈值。
(2) NDVI法与NDWI法。许多学者利用归一化植被指数法(NDVI)来提取水体信息,在GF-2卫星影像中,即第4波段与第3波段灰度值的差与和的比值,即
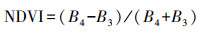 (2)
(2) 归一化水体差异指数(NDWI)的构建,是依据水体信息在绿光波段及近红外波段有较强的反射和吸收的特性,建立的水体信息提取方法[12]。即第2波段与第4波段灰度值差与和的比值,以GF-2影像数据为例,其式如下
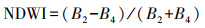 (3)
(3) (3) SWI法和MSWI法。阴影水体指数法(SWI)是在文献[13]中提出的。在可见光范围内,水体反射率总体较低,一般为4%~5%,且有着随波长增大而降低的特点。水体反射率在绿波段与蓝波段表现最高,近红外波段最低,几乎被完全吸收,依据此特点构建了SWI法,即
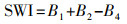 (4)
(4) 改进的阴影水体指数法(MSWI)由王瑾杰等在阴影水体指数法的基础上改进而来[14]。根据GF-2影像4个波段对水体反射率表现出的不同特性,反射率最高的蓝波段与反射率最低的近红外波段灰度值之差,再除以近红外波段,能够加大水体与阴影之间的区分,结合单波段阈值法构成决策树能够取得更好的水体提取结果。MSWI法如下
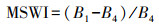 (5)
(5) 式中, B1、B2、B4分别表示GF-2影像中的蓝色波段、绿色波段和近红外波段。上述两种方法一定程度上能够区分阴影和水体,提高水体提取的精度。
2.2 水体提取结果分别采用上述5种方法对2个研究区进行水体信息提取,提取结果分别如图 2、图 3所示。

|
| 图 2 研究区1提取结果 |

|
| 图 3 研究区2提取结果 |
从图 2可知,研究区1范围内有建筑物等地物及阴影,在提取水体时效果受到一定程度的影响,其中NDWI法提取效果最好。图 3对于山区中水体,5种方法都能得到较好的提取效果。由此可知同一种提取方法在不同的区域具有不同的适用性,选择水体提取方法时应有针对性。
3 不同指数模型水体提取精度分析为比较不同水体提取模型提取水体的精度和稳定性,分别计算研究区1和研究区2水体采样区内各指数模型的最小值、最大值和平均值,见表 1、表 2。
| 指数模型 | NIR | NDVI | NDWI | SWI | MSWI |
| 最小值 | 487.000 0 | -0.338 0 | -0.568 5 | -1 897.000 0 | -0.813 7 |
| 最大值 | 6 311.000 0 | 0.537 4 | 0.331 0 | 7 686.000 0 | 0.676 9 |
| 均值 | 1 796.651 7 | 0.082 6 | -0.186 1 | 302.999 0 | -0.504 3 |
| 指数模型 | NIR | NDVI | NDWI | SWI | MSWI |
| 最小值 | 283.000 0 | -0.430 4 | -0.487 6 | -897.000 0 | -0.829 8 |
| 最大值 | 4 710.000 0 | 0.425 6 | 0.490 9 | 3 471.000 0 | 0.668 6 |
| 均值 | 1 453.228 8 | 0.095 5 | -0.191 0 | 99.245 2 | -0.502 6 |
将最大值和最小值的差值100等分,记为d;分别以平均值m、m+d、m-d、m+2d和m-2d作为分割的阈值,计算各指数模型的总体精度和Kappa系数所能达到的最大值。最后以目视解译的水体真值做为参考,将各指数提取结果与其建立误差矩阵,从而利用Kappa系数和总体精度2个指标分析比较2个不同研究区水体提取模型的提取精度和稳定性[16]。研究区1和研究区2阈值对不同水体提取模型的提取精度影响见表 3、表 4。
| NIR | 阈值 | 1 680.171 7 | 1 738.411 7 | 1 796.651 7 | 1 854.891 7 | 1 913.131 7 | 差值 |
| 总体精度/(%) | 71.29 | 67.87 | 63.94 | 59.43 | 54.27 | 17.01 | |
| Kappa系数 | 0.287 7 | 0.254 3 | 0.220 9 | 0.187 7 | 0.155 3 | 0.132 4 | |
| NDVI | 阈值 | 0.065 1 | 0.073 8 | 0.082 6 | 0.091 3 | 0.100 1 | 差值 |
| 总体精度/(%) | 55.94 | 46.77 | 38.51 | 32.30 | 27.15 | 28.79 | |
| Kappa系数 | 0.165 2 | 0.116 3 | 0.081 5 | 0.059 7 | 0.043 7 | 0.121 5 | |
| NDWI | 阈值 | -0.204 1 | -0.195 1 | -0.186 1 | -0.177 1 | -0.168 1 | 差值 |
| 总体精度/(%) | 33.37 | 38.81 | 45.03 | 51.34 | 57.20 | 23.83 | |
| Kappa系数 | 0.063 2 | 0.082 7 | 0.108 4 | 0.139 1 | 0.173 0 | 0.109 8 | |
| SWI | 阈值 | 111.339 0 | 207.169 0 | 302.999 0 | 398.829 0 | 494.659 0 | 差值 |
| 总体精度/(%) | 22.61 | 32.69 | 45.39 | 57.22 | 66.31 | 43.70 | |
| Kappa系数 | 0.031 1 | 0.060 9 | 0.110 0 | 0.173 2 | 0.240 4 | 0.209 3 | |
| MSWI | 阈值 | -0.534 2 | -0.519 3 | -0.504 3 | -0.489 4 | -0.474 5 | 差值 |
| 总体精度/(%) | 33.37 | 40.00 | 46.84 | 53.15 | 58.77 | 25.40 | |
| Kappa系数 | 0.063 2 | 0.087 3 | 0.116 6 | 0.149 0 | 0.183 3 | 0.120 1 |
| NIR | 阈值 | 1 364.688 8 | 1 408.958 8 | 1 453.228 8 | 1 497.4988 | 1 541.768 8 | 差值 |
| 总体精度/(%) | 79.63 | 78.90 | 78.06 | 77.23 | 76.37 | 3.27 | |
| Kappa系数 | 0.600 0 | 0.585 9 | 0.569 9 | 0.554 0 | 0.537 5 | 0.062 5 | |
| NDVI | 阈值 | 0.078 3 | 0.086 9 | 0.095 5 | 0.104 0 | 0.112 6 | 差值 |
| 总体精度/(%) | 92.10 | 89.03 | 85.17 | 81.69 | 78.17 | 13.93 | |
| Kappa系数 | 0.842 9 | 0.782 5 | 0.707 1 | 0.639 6 | 0.572 0 | 0.270 9 | |
| NDWI | 阈值 | -0.210 5 | -0.200 7 | -0.191 0 | -0.181 2 | -0.171 4 | 差值 |
| 总体精度/(%) | 87.74 | 90.80 | 92.48 | 93.72 | 94.75 | 7.00 | |
| Kappa系数 | 0.757 3 | 0.817 2 | 0.850 4 | 0.874 9 | 0.895 3 | 0.138 0 | |
| SWI | 阈值 | 11.885 2 | 55.565 2 | 99.245 2 | 142.925 2 | 186.60 52 | 差值 |
| 总体精度/(%) | 75.05 | 79.82 | 82.38 | 84.62 | 86.89 | 11.85 | |
| Kappa系数 | 0.512 3 | 0.603 6 | 0.653 1 | 0.696 5 | 0.740 7 | 0.228 4 | |
| MSWI | 阈值 | -0.532 5 | -0.517 5 | -0.502 6 | -0.487 6 | -0.472 6 | 差值 |
| 总体精度/(%) | 91.86 | 93.07 | 94.13 | 95.05 | 95.76 | 3.90 | |
| Kappa系数 | 0.838 2 | 0.862 0 | 0.883 0 | 0.901 2 | 0.915 4 | 0.077 2 |
从表 3中可以看出,当选用一定的阈值时,上述5种模型水体提取所能达到的精度由高到低依次为NIR、SWI、MSWI、NDWI、NDVI。相同的阈值变化程度下,阈值对精度稳定性影响最大的是SWI法,即在用SWI法对水体提取时,只要阈值稍微有波动,就会对精度造成较大的影响。稳定性最好的为NIR单波段阈值法。
表 4中可以发现,5种模型水体提取所能达到的精度由高到低依次为MSWI、NDWI、NDVI、SWI、NIR。相同的阈值变化程度下,阈值对精度稳定性影响最大的为NDVI法。当阈值发生5个相同的变化程度时,总体精度相差值为13.93。稳定性最好的为NIR单波段阈值法。
综合分析表 3和表 4可以发现对于不同的研究区域,相同的提取模型所能达到的提取精度不同,阈值对精度的影响程度也不同。研究区1中当选用一定的阈值时NIR法精度最高,阈值对其精度的稳定性影响最小;NDVI法提取精度最低,阈值对SWI法精度的影响程度最高。研究区2中MSWI法提取精度最高,NIR法提取精度最低;阈值对NDVI法提取精度影响最大,对NIR影响最小。
4 结论(1) 本文选用了5种不同的水体提取方法,对2个不同研究区进行了水体信息提取,并分析比较了提取结果。在对城区中的水体进行提取时,受城区建筑物、阴影等因素的影响,5种方法提取效果大不相同,在研究区1中NDWI法水体提取效果最好。研究区2中由于没有建筑物等地物因素的影响,5种方法的提取效果相当,并没有太大的差距。
(2) 利用水体指数模型提取水体时,阈值的选取影响着水体提取的精度。通过计算各指数模型相同变化幅度下的总体精度和Kappa系数所能达到的最大值,分析了阈值在2个研究区内对于不同的指数模型的水体提取精度及稳定性。结果显示相同阈值变化范围内,不同指数模型在同一研究区内阈值对水体提取精度的影响程度不同;相同水体指数模型在不同研究区内阈值对水体提取精度影响程度也不同。
| [1] |
付勇勇, 王旭航, 邓劲松, 等. 采用国产GF-2遥感影像的复杂水网平原水体信息提取[J]. 浙江大学学报(工学版), 2017, 51(12): 2474-2480. DOI:10.3785/j.issn.1008-973X.2017.12.022 |
| [2] |
孙金彦, 钱海明, 王春林. 基于GF-1遥感影像的河湖水域面积提取[J]. 江淮水利科技, 2016(3): 46-48. DOI:10.3969/j.issn.1673-4688.2016.03.020 |
| [3] |
靳海霞, 潘健. 基于高分二号卫星融合数据的城镇黑臭水体遥感监测研究[J]. 国土资源科技管理, 2017, 34(4): 107-117. |
| [4] |
彭凯锋, 贾永红, 李辉. 基于LBV变换的GF-2影像水体提取方法[J]. 北京测绘, 2018, 32(4): 394-398. |
| [5] |
黄帅, 丁建丽, 李艳华. 面向对象的国产GF-1遥感影像水体信息提取研究[J]. 人民长江, 2016, 47(5): 23-28. |
| [6] |
邓富亮, 章欣欣, 花利忠, 等. 基于国产高分辨率光学遥感影像的水体提取[J]. 水文地质工程地质, 2017, 44(3): 143-150. |
| [7] |
巩琳琳, 黄强, 孙清刚, 等. 刘家峡水库调度方式对黄河上游水文情势的影响[J]. 干旱区资源与环境, 2013, 27(2): 143-149. |
| [8] |
陈业培, 孙开敏, 白婷, 等. 高分二号影像融合方法质量评价[J]. 测绘科学, 2017, 42(11): 35-40. |
| [9] |
左梦颖. 基于高分二号数据的遥感影像融合方法研究[J]. 黑龙江科技信息, 2017(11): 130-131. DOI:10.3969/j.issn.1673-1328.2017.11.123 |
| [10] |
肖昶, 余晓敏, 韩逸飞. 高分二号卫星影像融合技术研究[J]. 地理空间信息, 2018, 16(6): 13-16. DOI:10.3969/j.issn.1672-4623.2018.06.004 |
| [11] |
郑雅兰, 王雷光, 陆翔. 高分二号全色-多光谱影像融合方法对比研究[J]. 西南林业大学学报(自然科学), 2018, 38(2): 103-110. |
| [12] |
MCFEETERS S K. The use of the normalized difference water index (NDWI) in the delineation of open water features[J]. International Journal of Remote Sensing, 1996, 17(7): 1425-1432. DOI:10.1080/01431169608948714 |
| [13] |
陈文倩, 丁建丽, 李艳华, 等. 基于国产GF-1遥感影像的水体提取方法[J]. 资源科学, 2015, 37(6): 1166-1172. |
| [14] |
王瑾杰, 丁建丽, 张成, 等. 基于GF-1卫星影像的改进SWI水体提取方法[J]. 国土资源遥感, 2017, 29(1): 29-35. |
| [15] |
熊金国, 王世新, 周艺. 不同指数模型提取ALOS AVNIR-2影像中水体的敏感性和精度分析[J]. 国土资源遥感, 2010, 22(4): 46-50. |



