2. 西安石油大学计算机学院, 陕西 西安 710065
2. School of computer, Xi'an Shiyou University, Xi'an 710065, China
高光谱图像虽然具有很高的光谱分辨率,但空间分辨率却普遍不高,这就导致高光谱图像中的每个像元可能不仅包含一种地物,而是多种地物覆盖类型的混合。对于这种光谱混合像元,无法根据提取的光谱特性判断其物质属性,也不能在分类过程中简单地将其归于某一类地物。混合像元在高光谱图像中的普遍存在使得传统的像元级图像分类和分割精度难以提高,是高光谱遥感技术向定量化方向发展的严重障碍。混合像元分解是解决该问题的有效方法,它能够在亚像元尺度上获取像元内部地物分布的真实信息,提高图像分类的精度。
根据混合像元的产生机理,高光谱图像混合模型可以分为线性混合和非线性混合两种模型。在传统的线性光谱混合像元分解算法中,一般假设图像中的像元都包含全部的端元光谱,对每个端元给出一个对应的丰度估计,但这往往与实际情况并不相符[1-4]。
实际上混合像元并不一定包含所有端元,而是由其中的一小部分端元混合而成,即混合像元只包含一个端元子集。混合像元中实际所包含的端元也互不相同,因此混合像元所包含的端元是可变的。常用的线性混合模型在混合像元分解过程中将所有的端元都纳入考虑范围,对每个端元向量都进行丰度估计,因此存在过拟合的分解误差。为了解决混合像元端元可变问题,国内外一些学者对如何选择混合像元的最优端元子集作了一些研究。国外学者主要提出了多端元光谱混合分析(MESMA)[5-6]、迭代光谱混合分析(ISMA)[7]和端元可变线性混合模型(EVLMM)[8]等最优端元子集选择方法。MESMA算法从光谱库中选择端元,假设每个像元最多由3个端元混合,尝试对所有端元的组合进行光谱分解,运算效率较低,光谱分解的误差较大。ISMA采用迭代算法去除丰度最小的端元,采用非限制性光谱分解方法进行丰度估计,根据混合像元光谱与剩余端元重建光谱之间均方根误差RMSE的变化情况确定最优端元子集。EVLMM基于端元组合数量由少到多进行搜索,直到采用更多的端元进行光谱重建后所得RMSE比上一步大时停止。文献[9]提出的OESSA算法首先利用所有端元进行非限制性光谱分解,然后根据丰度值量化重要程度的大小,对端元进行排序,由丰度最大的端元开始,逐渐增加端元个数解混,根据RMSE的统计结果确定最优端元子集。文献[10]提出了一种端元子集的局域确定方法,首先利用所有端元对混合像元进行分解,根据该像元邻域内各端元的丰度分布状况直接判定是否为纯像元,如果不是纯像元,则根据邻域内端元的丰度累加值大小排序,去掉累加值最小的端元,进行精度更高的二次解混。混合像元的端元可变性在实际中对应于混合像元的丰度矩阵具有稀疏特性。文献[11—15]尝试把稀疏原理与高光谱混合像元分解相结合,提出了基于稀疏约束的混合像元分解算法,基于稀疏约束的混合像元分解算法是在已知一个过完备的光谱库的情况下,寻找方程的最简单的解。
以上方法从不同思路对混合像元的可变性进行了研究,但实际上混合像元一般分布于不同地物的交界地带,不同地物交界处的混合像元所包含的端元最有可能与周围的地物分布状况相关。针对这种情况,本文提出一种利用图像的空间信息选取最优端元组合的混合像元分解方法,在混合像元周围局部邻域提取纯净像元光谱,与从整幅图像中提取到的全部端元进行对比,根据分解后RMSE的变化情况优化端元组合,对混合像元进行分解,从而获得最佳的光谱分解结果。
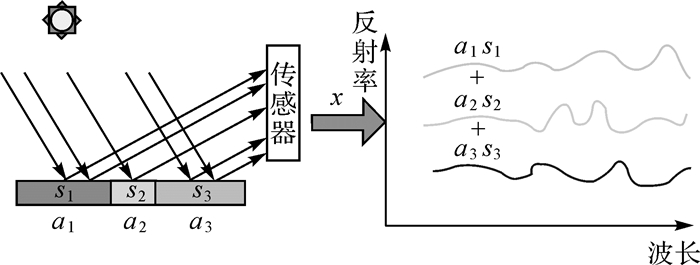
1 理论基础 1.1 线性混合模型线性混合模型(如图 1所示)是假定混合像元光谱由各端元的光谱通过线性叠加混合而成,由于其原理简单,物理含义明确,运算效率高,分解精度基本满足实际应用的需求,因而获得了广泛的应用。
|
| 图 1 线性光谱混合模型 |
图 1形象地阐述了线性光谱混合过程,在地面的3种物质分别为a1、a2和a3,所占面积的比例分别为s1、s2和s3,阳光照射在这3种地物上,互不干扰,而在成像光谱仪上形成一个混合像素点,混合像元得到的反射率为x=a1s1+a2s2+a3s3,它是各个光谱特征的线性叠加。
线性光谱混合模型的数学表达式为
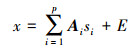 (1)
(1) 式中,x为混合像元的反射率;Ai为像元的第i个端元向量;si为该像元内第i个端元的反射率比例(即丰度);E为模型误差;p为端元数目。
式(1)中各端元的丰度没有数学限制,因而称为非限制性线性混合模型(FCLS)。若si受以下两个条件的约束: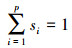
对混合像元的分解结果所进行的评价分为定性评价和定量评价两种。定性评价主要是通过目视的方式对分解后的端元分布丰度图进行观察,并与实际地物的分布状况进行对比。为了对混合像元的分解结果进行准确客观的评价,需要建立相关的评价指标进行定量评价,定量评价通过严格的数学计算分解,给出精确的对比评价结果,因而获得了广泛的应用。对真实高光谱图像进行混合像元分解时,端元光谱和端元对应的丰度图像信息一般是未知的,均方根误差是一种比较简单、常用的混合像元分解精度定量评价指标。
假设混合像元原始光谱向量为X,光谱分解所得的端元矩阵为A,丰度向量为S,则光谱重构后的光谱向量为
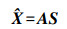 (2)
(2) 该像元的余差为
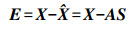 (3)
(3) 对于n维的光谱向量,均方根误差为
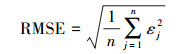 (4)
(4) 式中, εj为余差向量中的元素。获得的RMSE值越小说明算法的混合像元分解精度越高,算法越有效。
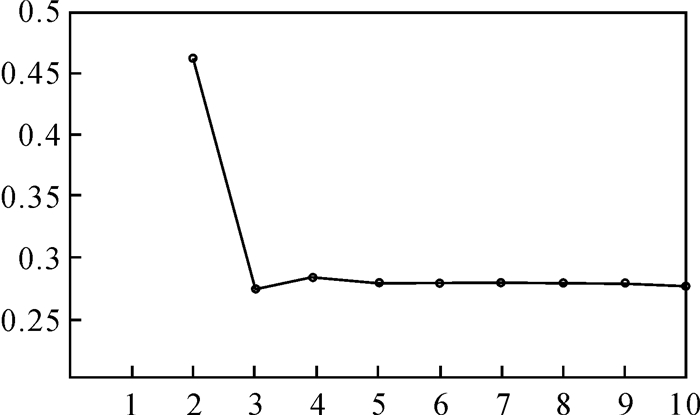
2 光谱分解误差随端元子集变化情况现有的研究表明,利用图像中的所有端元对混合像元进行分解,得到各端元的丰度值,然后从丰度最大的端元开始,按照丰度从大到小的顺序,逐渐添加端元,建立并扩充端元子集,用这些端元子集分别对该混合像元进行二次分解,则混合像元分解的误差总体上趋于减小[9]。
如对于整幅图像包含10个端元、实际上由3个端元组成的混合像元,图 2给出了RMSE随端元子集中端元数目增加的变化趋势。
|
| 图 2 光谱分解误差随端元子集扩充的变化趋势 |
在混合像元分解时,如果端元子集中漏选实际存在的端元,那么光谱重构图像与原始图像的RMSE会很大;当端元子集中恰好包含实际存在的端元时,RMSE最小;而当端元子集中多选了冗余端元进行分解时为无偏估计,RMSE变化很小。
图 2中,按照丰度排序,在利用其中3个丰度最大的端元进行混合像元二次分解后,相比上一步2个端元分解时重构光谱与原始光谱之间的RMSE急剧下降,再向端元子集中增加端元数量进行分解,RMSE的变化也不大,而是趋于平缓,由此可以判断曲线“拐点”对应的端元集就可以作为组成该混合像元的最优端元子集,该混合像元实际包含的端元数为3。
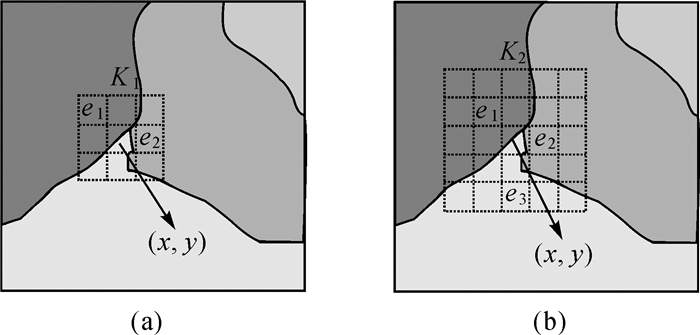
3 结合图像空间信息的最优端元子集选择当图像中地物种类较多、存在较多端元的时候,如果通过全局搜索的方式在全部端元中搜索混合像元的最优端元组合效率较低,因自然界地物往往具有一定的空间结构,如农田、森林、草地、建筑物,湖泊等,这些不同种类地物区块之间光谱差异明显。光谱混合像元一般位于地物区块的边缘交界地带,在混合像元的周围存在纯净像元的可能性较大,而这些纯净像元的光谱往往就是组成混合像元的端元光谱。充分利用图像的空间信息,从混合像元的就近邻域开始寻找纯净像元,搜索确定混合像元的最优端元组合,可以提高搜寻混合像元最优端元子集的效率。如图 3所示,本文提出一种结合图像的空间信息寻找混合像元最优端元子集的方法。具体步骤如下:
|
| 图 3 扩大结构元素寻找最优端元子集 |
(1) 定义一个结构元素K,K是一个中心像元坐标为(x, y)、边长为k的正方形。让结构元素K在图像上滑动,在结构元素覆盖的区域内计算所有像元光谱向量均值
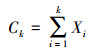 (5)
(5) 计算结构元素覆盖区域内k2个像元的光谱向量到均值光谱向量Ck的欧氏距离,记为dk。
(2) 根据凸面几何学理论,最大dk对应的像元必然是结构元素覆盖的局部区域内“最纯”的像元,将其记为第1个“端元”e1;然后将结构元素k2个像元中距离e1最远的像元记为第2个“端元”e2;距离e1和e2所构成直线最远的像元(这个点向e1和e2所构成的直线作垂线距离最远)记为第3个“端元”e3;距离e1、e2和e3所构成平面最远的像元记为第4个“端元”e4;以此类推,最多得到k2个“端元”e1, e2, …, ek。
(3) 对步骤(2)中获得的“端元”ei,与从整幅图像中提取的所有端元ai(i=1, 2, …, m)进行对比,计算它们之间的光谱夹角距离
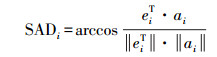 (6)
(6) 如果光谱夹角SADi小于设定的阈值,光谱高度相似,则可以将对应的端元ai加入结构元素K覆盖区域中心位置处混合像元的最优端元子集中。此步骤本质上是通过结构元素K在混合像元附近邻域寻找“纯像元”光谱作为混合像元的端元光谱,这符合混合像元一般位于地物区块边缘交界地带的规律,实际上是利用了图像的空间信息就近寻找混合像元的最优端元子集。
(4) 最优端元子集建立后,应用全限制线性混合模型对混合像元进行分解,然后计算重构光谱与原始光谱的RMSE。如果该RMSE近似等于全端元a1, a2, …, am分解时与原始光谱之间的RMSE,则当前的端元子集即为最优;如果该RMSE远大于全端元a1, a2, …, am分解时的RMSE,则说明端元子集中缺少实际存在的端元。
(5) 增大结构元素K(x, y)的尺寸(增大边长k),扩大搜索范围,返回步骤(1)重复执行,直到RMSE减小到近似全端元分解时的RMSE为止,最终得到混合像元的最优端元子集,进而得到最优的光谱分解结果。
图 3为扩大结构元素寻找最优端子集示意图。图 3(a)中结构元素K1边长为3,结构元素内只包含两种物质的纯像元,因此只能找出结构元素中心位置处混合像元(x, y)包含的两个端元e1和e2;扩大结构元素,使其边长为5(如图 3(b)所示),结构元素内涵盖3种物质的纯像元,即可找到混合像元(x, y)的全部端元e1、e2和e3。
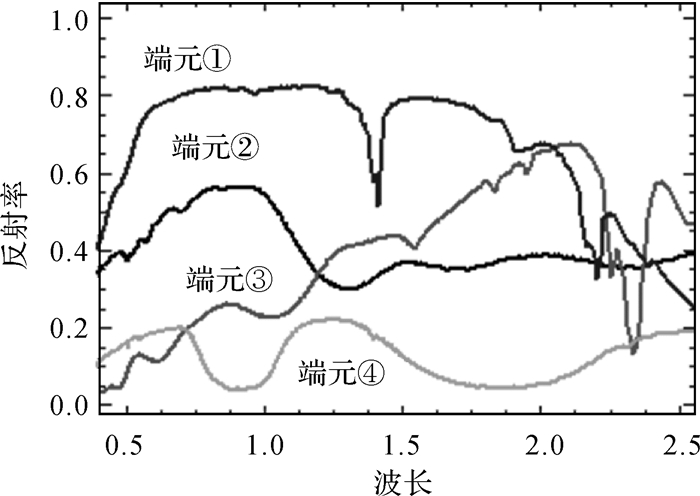
4 试验与讨论 4.1 模拟图像试验在USGS[16]矿物光谱库中选择4种矿物光谱作为端元,其光谱曲线如图 4所示。
|
| 图 4 从USGS光谱库中选择的4个光谱 |
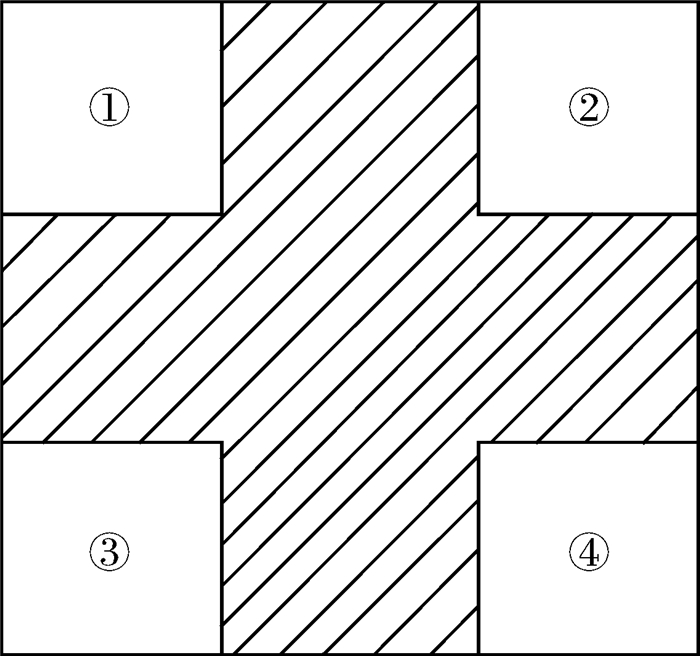
添加SNR=30dB的高斯噪声,构建大小为200×200的模拟图像。如图 5所示,模拟图像4个角上分布着4个端元的纯像元,阴影部分是由4种端元混合而成的混合像元。
|
| 图 5 模拟图像 |
以4个端元的其中一个进行分析,图 6为端元①的实际丰度图及分别采用UCLS、FCLS、迭代光谱混合分析(ISMA)及本文所提出的端元可变混合像元分解方法解混后的丰度图。图中颜色由浅到深表示丰度逐渐增加。

|
| 图 6 端元①的丰度分布 |
试验数据见表 1,可以看出,UCLS由于没有添加丰度约束条件,因而产生了最小的RMSE,由于对丰度和没有进行约束,丰度和在0.95~1.05之间的像元仅占图像中像元的69.35%;FCLS严格满足和为1的约束条件,但RMSE较大,分解精度较低。ISMA算法的RMSE也比FCLS大。本文提出的算法在RMSE上优于ISMA算法,并且最后的分解结果丰度和满足和为1的要求。
| 算法 | RMES | 丰度和 | ||
| 最小值 | 最大值 | 0.95%~1.05% 中像元占比 /(%) |
||
| UCLS | 0.006 2 | 0.862 | 1.153 | 69.35 |
| FCLS | 0.010 6 | 1 | 1 | 100 |
| ISMA | 0.009 6 | 0.865 | 1.132 | 89.58 |
| 本文算法 | 0.007 1 | 1 | 1 | 100 |
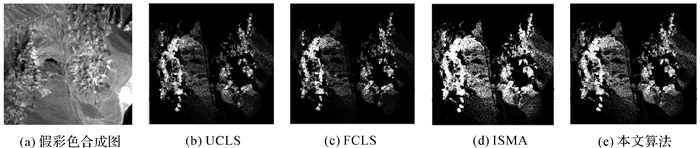
美国内华达州Cuprite地区矿物品种多样,各种矿物露头良好,该地区的AVIRIS数据包含224个波段(0.4~2.5 μm),空间分辨率和光谱分辨率分别为20 m和10 nm,适合检验混合像元分解算法的性能。去除其中受水蒸气吸收影响较大和低信噪比的波段(1~3、104~113、148~167、221~224),保留187个波段,经过辐射校正得到反射率数据,并选取其中200×200大小的区域用于试验。图 7为该区域的假彩色合成图与执行UCLS、FCLS ISMA及本文算法所得到的其中一个端元丰度的分布图。
|
| 图 7 Cuprite地区AVIRIS数据假彩色合成图及光谱分解后各端元丰度分布 |
表 2是对试验所得结果的数据分析。结果表明,UCLS算法的RMES最小,但图像中仅有11.8%的像元丰度和在0.8~1.2之间。FCLS算法虽然满足丰度和为1的约束条件,但RMES最大。相比本文算法,ISMA算法的RMSE较大,丰度和也不满足和为1的约束条件。本文方法在选定最优端元子集进行二次分解时,采用的是FCLS算法,丰度和为1。因此本文所提算法在性能上是优于ISMA的。
| 算法 | RMES | 丰度和 | ||
| 最小值 | 最大值 | 0.8%~1.2% 中像元占比 /(%) |
||
| UCLS | 0.003 6 | -5.6 | 6.53 | 11.8 |
| FCLS | 0.005 3 | 1 | 1 | 100 |
| ISMA | 0.004 9 | 0.28 | 1.98 | 73.6 |
| 本文算法 | 0.003 9 | 1 | 1 | 100 |
本文方法利用图像的空间信息,用结构元素搜索周围邻域的“纯像元”光谱,优先组成最优端元子集,进行光谱分解。表 2中真实高光谱数据的试验结果再次表明,采用本文方法优化后的端元子集进行光谱分解结果在RMSE上优于FCLS和SALSA;且在二次分解时采用FCLS算法,因此丰度和为1,符合实际情况,总体上达到了较好的光谱分解效果。
5 结语混合像元分解是高光谱遥感信息提取的常用方法。传统的分解方法一般假设混合像元包含图像中的所有端元,但这并不符合实际情况,因此导致分解结果对噪声敏感,分解精度不高。实际的混合像元只包含少数端元,由于地物空间分布上的连续性,混合像元所包含的端元往往与附近区域分布的地物有关。
本文结合图像空间信息,用一个空间结构元素在混合像元附近区域就近确定选取最优端元子集。相比其他方法,该方法既不需要遍历图像中所有端元, 且通过迭代运算来寻找最优端元子集,也不需要按照初次解混后的丰度大小进行排序后对端元进行取舍,而是将附近邻域的“纯像元”光谱优先加入最优端元子集,从最有可能属于该混合像元的端元开始搜索添加,这符合现实地物分布的实际情况,有利于提高最优端元子集的搜索效率,最终获得较好的分解效果。
| [1] |
ZARE A, HO K. Endmember variability in hyperspectral analysis:addressing spectral variability during spectral unmixing[J]. IEEE Signal Processing Magazine, 2014, 31(1): 95-104. |
| [2] |
WU K, ZHANG L, NIU R, et al. Super-resolution land-cover mapping based on the selective endmember spectral mixture model in hyperspectral imagery[J]. Optical Engineering, 2011, 50(12): 126201. DOI:10.1117/1.3660527 |
| [3] |
ZHANG L, DU B, ZHONG Y. Hybrid detectors based on selective endmembers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2633-2646. DOI:10.1109/TGRS.2010.2040284 |
| [4] |
KUMAR U, RAJA S K, MUKHOPADHYAY C, et al. Assimilation of endmember variability in spectral mixture analysis for urban land cover extraction[J]. Advances in Space Research, 2013, 52(11): 2015-2033. DOI:10.1016/j.asr.2013.08.022 |
| [5] |
FRANKE J, ROBERTS D A, HALLIGAN K, et al. Hierarchical multiple endmember spectral mixture analysis (MESMA) of hyperspectral imagery for urban environments[J]. Remote Sensing of Environment, 2009, 113(8): 1712-1723. DOI:10.1016/j.rse.2009.03.018 |
| [6] |
TITS L, SOMERS B, HEYLEN R, et al. Improving the efficiency of MESMA through geometric unmixing principles[C]//SPIE Remote Sensing.[S.l.]: International Society for Optics and Photonics, 2013: 88920Q.
|
| [7] |
ROGGE D M, RIVARD B, ZHANG J, et al. Iterative spectral unmixing for optimizing per-pixel endmember sets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(12): 3725-3736. DOI:10.1109/TGRS.2006.881123 |
| [8] |
RAKSUNTORN N. Unsupervised spectral mixture analysis for hyperspectral imagery[M]. Starkville: Mississippi State University, 2009.
|
| [9] |
李二森.高光谱遥感图像混合像元分解的理论与算法研究[D].郑州: 信息工程大学, 2011.
|
| [10] |
王立国, 张晶. 基于线性光谱混合模型的光谱解混改进模型[J]. 光电子·激光, 2010, 21(8): 1222-1226. |
| [11] |
IORDACHE M D, PLAZA A, BIOUCAS-DIAS J. On the use of spectral libraries to perform sparse unmixing of hyperspectral data[C]//Hyperspectral Image and Signal Processing: Evolution in Remote Sensing.[S.l.]: IEEE, 2010: 1-4.
|
| [12] |
IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Sparse unmixing of hyperspectral data[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(6): 2014-2039. |
| [13] |
CHEN F, ZHANG Y. Sparse hyperspectral unmixing based on constrained lp - l2 optimization[J]. IEEE Geoscience & Remote Sensing Letters, 2013, 10(5): 1142-1146. |
| [14] |
IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Hyperspectral unmixingwith sparse group lasso[C]//Geoscience and Remote Sensing Symposium.[S.l.]: IEEE, 2011: 3586-3589.
|
| [15] |
IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Collaborative sparse regression for hyperspectral unmixing[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(1): 341-354. |


