2. 广西空间信息与测绘重点实验室, 广西 桂林 541004;
3. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079;
4. 武汉大学测绘学院, 湖北 武汉 430079
2. Guangxi Key Laboratory of Spatial Information and Geomatics, Guilin 541004, China;
3. GNSS Research Center, Wuhan University, Wuhan 430079, China;
4. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
地球冰冻圈内的积雪占据了全世界约1/6的淡水资源,是全球水循环过程中重要组成部分之一。积雪深度的变化量是用来进行雪水当量估算、地表辐射平衡、流域水平衡等研究的一个重要参数,同时可为下游的洪灾预警和水力发电提供信息[1]。因此,监测雪深对于管控水资源具有重要意义。目前,全球大多数区域的雪深观测资料尚不充足,一方面是由于常规的雪深测量技术(主要为人工测量或超声波测深仪)缺乏较高的时空分辨率,另一方面是卫星图像遥感更适用于监测积雪覆盖度而非积雪的深度和密度[2]。针对以上的问题,基于信噪比(signal-to-noise ratio, SNR)的GPS-R技术遥测GNSS测站周围的雪深参数已成为一种新手段,具有范围广、全天候、费用低等优势[3]。
目前,基于GPS-R技术遥测表层环境参数已成为国内外的研究热点之一,研究领域由海洋遥感扩展到陆地遥感,可适用于海面测高、海面风速、土壤湿度、雪深等[4-7]。最初GPS-R技术一般使用双天线GNSS接收机,同时使用方向向上的右旋圆极化天线和方向向下的左旋圆极化天线分别接收GPS卫星直射信号和反射信号,该方法能简单有效地分离直射分量和反射分量,获取不同厚度的积雪表层的反射情况,但其特殊性导致价格高昂[8]。因此,现有的GPS-R研究主要采用单天线的大地测量型GNSS接收机,但反演精度有待提升。文献[5,9—10]利用连续运行参考站(CORS)的GPS观测数据,提出了多路径信号的振幅和相位变化量与接收机周围土壤水分存在相关性。随后,文献[11—12]利用直射分量和反射分量组成的复合信号SNR数据,将GPS多路径的应用扩展到测量长时间的雪深数据,表明雪深的变化同样能够很清晰地被多路径调制跟踪。文献[13]展示了GPS L2P波段的信噪比数据反演积雪深度,并与L1 C/A的结果对比,结果表明L2P信号频率低于L1 C/A,但是其与L1 C/A的结果无显著差异。与上述的基于信噪比数据提取多路径信息不同,文献[14]引入了GPS无几何距离组合观测L4(L1、L2载波的相位观测线性组合)的概念并进行了雪深探测的研究,获得了略差于信噪比的反演结果。同时,文献[15]SNR数据与L4相位组合值反演分析了雪深数据,并与GPS SNR观测值融合来提高反演精度。
基于信噪比方法反演雪深可以独立应用于单个载波,而其反演性能在很大程度上取决于SNR数据的观测质量和直接路径分量的去除。目前,GPS-R技术反演雪深仍处于前期的理论阶段,反演模型基于假设的理想状态,运用经验参数设置阈值,确定反射信号的有效性。为了改进有效的GPS反射观测量,本文利用GPS跟踪站提供的新型L5信号作为数据源,结合实测雪深资料,研究GPS多路径反射信号与积雪深度的特征关系,分析反演结果,探讨GPS反射信号反演积雪特征的适用范围。
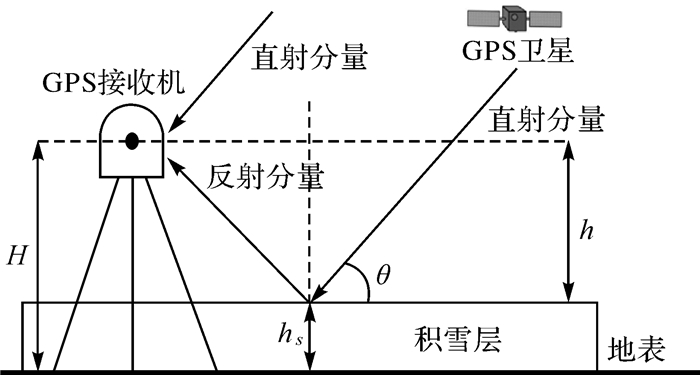
1 GPS-R遥测雪深理论概述目前,GPS多路径已成为限制高精度定位的重要误差源,主要受反射层的结构和介质等影响。本文使用单天线GNSS接收机,可同时接收直射信号及来自积雪层等多路径影响的反射信号[16]。GPS-R技术反演雪深使用的是复合信号中的多路径信息,尽管测地型接收机的扼流圈和抑径板等能有效减小多路径效应但并未完全被消除,且低高度角时反射信号的极化变化很小,反射分量进入接收机后易与直射分量形成干涉,在低高度角下引起严重的信号震荡,此为GPS反射信号测量雪深的理论基础[17]。为方便处理卫星数据,在反演模型中,假设反射面无明显的倾斜且暂不考虑信号穿透积雪层,图 1为仅考虑了GPS信号经水平反射面反射后被接收机接收的几何模型。接收机天线同时接收卫星的直接信号分量Sd和经反射面反射的多路径信号Sr,θ为卫星高度角,h为接收机天线与积雪反射面间的垂直距离,H为无雪时地表与天线间的垂直距离,hs为积雪层的深度。
|
| 图 1 GPS-R技术反演雪深的几何模型 |
为精确反演地表雪深,应预处理合适的卫星观测数据。当电离层活动不剧烈时,L4的反演雪深精度仍差于SNR数据,考虑从SNR数据中提取多路径信息相较于GPS相位观测值更简便,因此利用GPS卫星反射信号的SNR数据反演雪深具有明显优势。
信噪比数据是表示接收机天线接收的卫星信号强度的一个量值,单位为dB。卫星信号的发射功率、天线增益强度、卫星与接收机天线的直线距离及多路径效应等是影响信噪比变化的主要因素。对于接收的复合信号与直射分量、反射分量的信噪比数据来说,三者的关系如下[13]
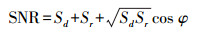 (1)
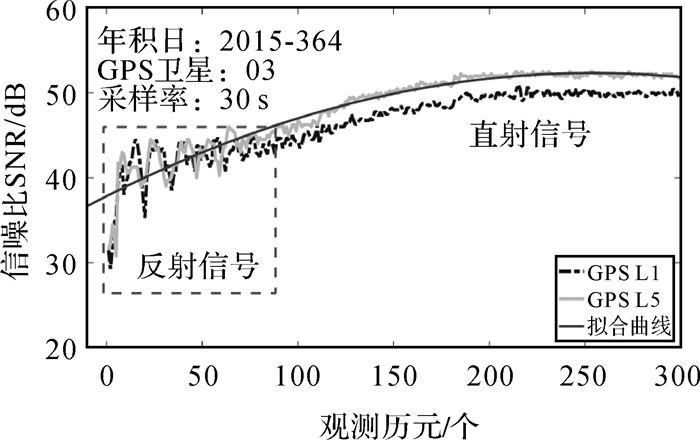
(1) 式中,Sd和Sr为直射分量和反射分量的信号功率;cos φ为两种信号分量的夹角余弦值。图 2为2015年第364年积日加拿大YEL2测站PRN 03号卫星信噪比数据的时间序列,其中,横轴为连续的观测历元,纵轴为信噪比数据,观测采样率为30 s。研究表明,天线增益强度在较高的卫星高度角下得到加强,SNR数值被有效提高;而在低卫星高度角下,因接收机天线的增益强度减弱及存在多路径效应使得SNR数值下降较严重。由图 2可见,较低的高度角下,SNR数据会受到较强的多路径影响,其数值比高高度角下明显减小且变化量急剧加大,因此可利用低高度角的GPS卫星反射信号信噪比数据评价多路径效应。相反,多路径效应引起的信号反射会直接导致信噪比数据发生相应的变化。
|
| 图 2 GPS卫星L1和L5信号的信噪比变化 |
由于测量型接收机天线的扼流圈和天线增益能有效抑制因地表层反射引发的多路径信息,因此直射分量和反射分量的振幅之间存在Sd≫Sr的关系。直射分量是复合信号的整体趋势项且卫星通过单个完整周期,而反射分量的信号幅度小得多,且以更高的频率产生局部振荡,主要是在低高度角下由多路径所致(如图 2所示的虚框部分)。通过利用低阶多项式拟合建模,去除复合信号的趋势项(直接路径分量),以此获得去趋势项后的信噪比时间序列,即SNR残差序列(dSNR),具体如下
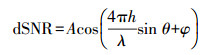 (2)
(2) 式中,A为信号振幅大小;λ为载波波长;θ为卫星高度角;φ为不足整周期的相位值。为了使复合信号的信噪比趋势由指数变化转化为线性变化,在去除趋势项前应由dB转化为比值(Volts/Volts),转换公式[13]如下
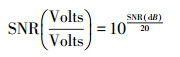 (3)
(3) 由于直射信号和反射信号经过不同的传播路径长度,两者会产生一段2hsinθ的波程差,相位延迟量ψ,可表示为[18]
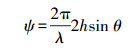 (4)
(4) GPS卫星、地表积雪层和接收机天线的几何位置关系会随着时间t不断缓慢变化,卫星高度角θ随之发生相应变化,复合信号的多路径相位延迟量ψ也随之呈周期性变化。该相位延迟量的变化率可由相位延迟与时间t求导数的获取。基于卫星高度角θ与时间t的对应关系,将t=sinθ代入式(4),可得
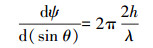 (5)
(5) 通过进一步简化式(5),可得GPS反射信号的主频率与接收机天线高度的比例关系为
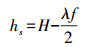 (6)
(6) 式中,hs为地表积雪深度;H为无积雪时接收机天线的高度;f为信号频率。由式(6)得,GPS反射信号频率成为解决GPS-R技术测量积雪深度的关键量。一般来说,信号频率的提取主要采用快速傅里叶变换的方法,但是该方法仅对整周期的信号具有显著效果。由于sinθ为非等间隔采样,因此可采用Lomb-Scargle周期图法进行非等间隔频谱分析来求取信号的频率值[19]。此外,Lomb-Scargle周期图法可从时域序列中提取出弱周期信号并减弱不均匀性产生的虚假信号。当地表存在积雪时,积雪深度发生变化,则天线高度h同时发生变化,通过此时的信号频率f可获取地表雪深信息,即达到GPS-R探测雪深的目的。
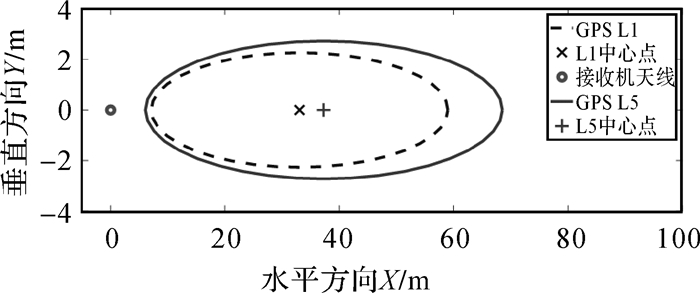
2 GPS-R技术的实例分析本次试验验证了基于新型的L5信号的GPS-R技术反演地表雪深参数的适用性和稳定性,主要利用了国际GNSS服务中心(IGS)的加拿大YEL2测站的实测GPS数据进行实例分析,观测时段为2015年9月—2016年7月。测站周围地形平坦,无雪时测站天线高为1.8m,观测间隔为30s,采集数据为GPS卫星L1和L5载波的信噪比数据,其中包含了全部的32颗MEO卫星。本试验未能顾及短时间内发生强降雪或地表的起伏度较大,此情况下需获取各时段内的雪深变化量,为简化数据处理的难度仅仅考虑一天内的各时段雪深平均值作为GPS-R技术的测量值。假设地面平坦时,反射信号的入射角最小值为5°。图 3显示了GPS-R技术测量雪深的椭圆覆盖区域,此时的探测面积最大,且L5的反射信号轨迹明显大于L1。该区域内应避免非地表雪层的其他反射源,选择反射轨迹位于地表相对平坦区域的卫星作为信号源。
|
| 图 3 卫星高度角5°的菲涅尔反射区 |
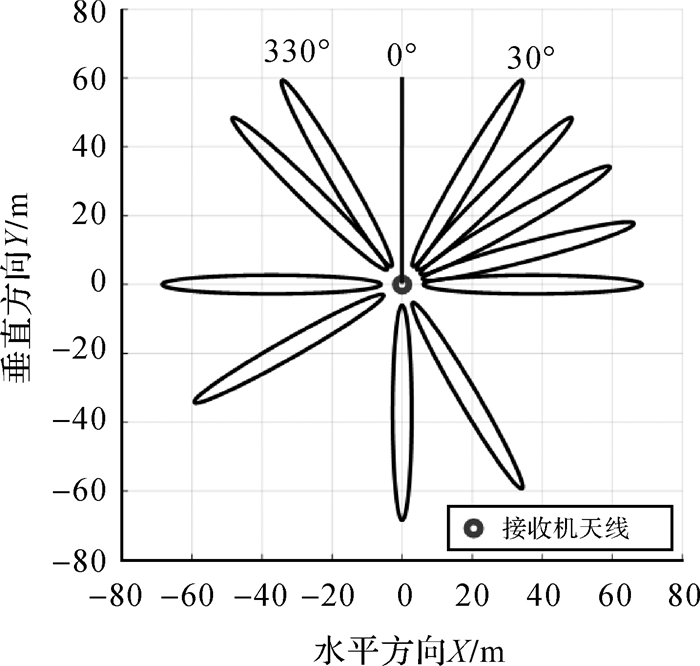
根据文献[20]的结果可知,GPS卫星轨迹存在一定的区域限制,以GPS接收机天线为中心形成了一个方位角在30°~330°内半径为2a的扇形区域,如图 4所示。由于接收机天线与反射面之间的垂直距离较小,陆基GPS-R技术的测量面积远小于空基和星基,但是陆基平台具有的成本低廉、操作简便及接收数据稳定等优点使得其在GPS-R理论研究方面更具优势。
|
| 图 4 不同弧段的卫星轨迹 |
同时,本次试验利用了加拿大Yellowknife Henderson(Y-H)气象监测站的实测雪深数据进行对比分析。该气象站与YEL2测站之间相距约2 km,由于两地的直线距离较小,因此两地实际雪深的变化并不明显,Y-H气象站提供的雪深数据作为真实值,可用于检验GPS-R技术反演雪深的可靠性。
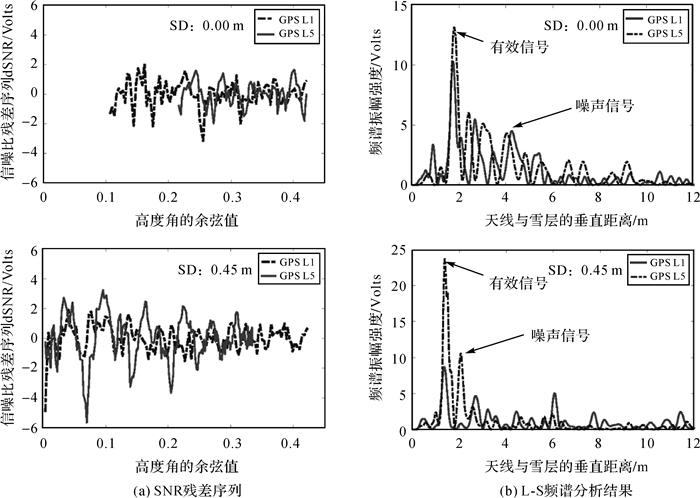
YEL2测站提供了GPS卫星L1、L5波段的信噪比数据,图 5给出了2015年第274和349年积日PRN 03号卫星的dSNR序列及Lomb-Scargle频谱分析特性图。由图 5可看出,GPS卫星L1和L5波段的反射信号均能获取到多路径信息,但是利用L5信号信噪比数据的频谱振幅强度的数值明显小于L1的结果,这样减小了利用L5信号提取主频信息的难度。
|
| 图 5 GPS卫星反射信号的dSNR序列与L-S频谱特性 |
图 5(a)中,通过去除整体趋势化处理后的dSNR序列近似于三角函数曲线,随着地表雪深逐渐加大,波峰(波谷)与波峰(波谷)之间的间距逐渐变大,即序列中波动的周期变大,振荡频率变小,而根据式(6),信号的振荡频率与反射高度为线性正相关。图 5(b)中,随着积雪深度的增大,频谱振幅强度的峰值变大,峰值对应的天线与雪层间反射高度变小。由于反射高度越小,地表雪深越大。因此,验证了雪深变化会导致GPS卫星反射信号信噪比数据的多路径分量频率产生规律性变化。
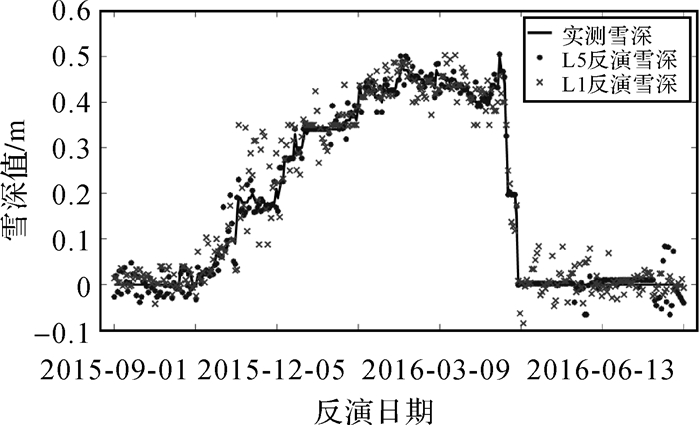
为了进一步验证GPS多路径信号反演雪深的探测质量,本文收集了2015年9月—2016年7月逐日的GPS观测数据及气象雪深数据,进行反演试验和对比分析。利用新型的L5信号反演地表雪深,并与L1的结果和实测雪深进行对比,如图 6所示。在反演雪深的时间段内,由于积雪深度发生明显上升,可明显看出至少出现5次强降雪,分别为2015年10月初、2015年11月末、2015年12月中旬、2016年2月初及2016年3月底。在雪深的变化过程中,GPS反射信号随之相应变化,因此雪深反演值与实测雪深在长时间序列上的趋势基本保持一致。
|
| 图 6 基于GPS-R技术反演雪深与实测雪深的对比 |
对不同时段的积雪深度分析表明:当雪深为0~10 cm时,由于反射面的结构复杂,反演结果波动较大,此时无法判定地表是否存在积雪,可能是夏季植被茂盛而导致;当雪深为10~35cm时,L1的雪深反演效果明显差于L5的结果,尤其是2015年12月初,地表积雪有部分消融,使得反演值与实测值的偏差加大,这可能是由于GPS测站与气象监测站的周边环境不同,使得积雪的消融快慢不同;当雪深为35~50 cm时,反演结果与实测数据的一致性良好,反演结果不但较好地体现了雪深的变化趋势,且与实测值的差值较小,验证了GPS-R技术可用于实时雪深监测的可行性,尤其是强降雪量地区。对于GPS-R技术反演雪深与实测雪深进行相关性分析,L5反演结果与实测值、L1反演结果与实测值、L1反演结果与L5反演结果的相关系数分别为0.96、0.89和0.91,L1和L5与实际雪深的RMSE值分别为2.1和4.0 cm。实测雪深与GPS-R反演雪深仍存在约3~4 cm的系统误差,其原因之一可能是提供实测雪深数据的Y-H气象站与YEL2测站有数千米的距离差异。通过上述分析,利用GPS卫星L1和L5载波的多路径反射信号反演雪深均是有效的,但是新型的GPS L5波段反射信号的信噪比数据在反演雪深的精度方面有所提高。
地表雪深变化量的准确和长期监测对于研究全球的气候科学具有重要的实际价值。本文系统分析了利用GPS-R技术反演雪深的理论基础,提出了以一种GPS卫星新型的L5载波的信噪比观测资料作为数据源,反演了YEL2测站附近的雪深变化,分别从载波变量、反射区域范围、信号频率、频谱振幅强度的变化规律及相关性分析等方面进行了分析,并与实测雪深数据进行比较,得出了较好的反演结果,初步验证了GPS-R遥感技术反演雪深的可行性;同时运用新型的L5信号在雪深反演方面明显优于L1反演结果,雪深反演精度和可靠性得到了有效提高。随着GNSS-R的发展,新的卫星、新的载波信号为多路径反射信号应用于反演雪深提供了更多潜在的可能性,从而进一步地完善GNSS-R反演模型。
基于GNSS-R遥感技术反演雪深具有独特优势和良好的应用前景,但目前国内的相关研究尚处于起步阶段,为获得更精确和准确的反演结果,仍需大量的研究。
| [1] |
冯学智, 柏延臣. 北疆地区积雪深度的克里格内插估计[J]. 冰川冻土, 2000, 22(4): 358-361. DOI:10.3969/j.issn.1000-0240.2000.04.011 |
| [2] |
金双根, 张勤耘, 钱晓东. 全球导航卫星系统反射测量(GNSS+R)最新进展与应用前景[J]. 测绘学报, 2017, 46(10): 1389-1398. DOI:10.11947/j.AGCS.2017.20170282 |
| [3] |
王娜子, 鲍李峰, 高凡. 宽巷组合下的cGNSS-R测高算法[J]. 测绘通报, 2016(8): 6-9. |
| [4] |
杨东凯, 刘毅, 王峰. 星载GNSS-R海面风速反演方法研究[J]. 电子与信息学报, 2018, 40(2): 462-469. |
| [5] |
LARSON K M, BRAUN J J, SMALL E E, et al. GPS multipath and its relation to near-surface soil moisture content[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2010, 3(1): 91-99. DOI:10.1109/JSTARS.2009.2033612 |
| [6] |
ZHOU W, LIU L, HUANG L, et al. Snow depth detection based on L2 SNR of GLONASS satellites and multipath reflectometry[C]//Proceedings of CSNC.[S.l.]: Springer, 2018: 221-231.
|
| [7] |
YU K. Tsunami-wave parameter estimation using GNSS-based sea surface height measurement[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2603-2611. DOI:10.1109/TGRS.2014.2362113 |
| [8] |
CARDELLACH E, FABRA F, RIUS A, et al. Characteri-zation of dry-snow sub-structure using GNSS reflected signals[J]. Remote Sensing of Environment, 2012, 124(11): 122-134. |
| [9] |
LARSON K M, SMALL E E, GUTMANN E, et al. Using GPS multipath to measure soil moisture fluctuations: initial results[J]. GPS Solutions, 2008, 12(3): 173-177. DOI:10.1007/s10291-007-0076-6 |
| [10] |
LARSON K M, SMALL E E, GUTMANN E D, et al. Use of GPS receivers as a soil moisture network for water cycle studies[J]. Geophysical Research Letters, 2010, 35(24): 851-854. |
| [11] |
LARSON K M, GUTMANN E D, ZAVOROTNY V U, et al. Can we measure snow depth with GPS receivers?[J]. Geophysical Research Letters, 2009, 36(17): L17502. DOI:10.1029/2009GL039430 |
| [12] |
NIEVINSKI F G, LARSON K M. Inverse modeling of GPS multipath for snow depth estimation—part Ⅱ: application and validation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6564-6573. DOI:10.1109/TGRS.2013.2297688 |
| [13] |
JIN S, QIAN X, KUTOGLU H. Snow depth variations estimated from GPS-reflectometry: a case study in Alaska from L2P SNR data[J]. Remote Sensing, 2016, 8(1): 63-77. DOI:10.3390/rs8010063 |
| [14] |
OZEKI M, HEKI K. GPS snow depth meter with geometry-free linear combinations of carrier phases[J]. Journal of Geodesy, 2012, 86(3): 209-219. DOI:10.1007/s00190-011-0511-x |
| [15] |
QIAN X, JIN S. Estimation of snow depth From GLONASS SNR and phase-based multipath reflectometry[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(10): 4817-4823. DOI:10.1109/JSTARS.2016.2560763 |
| [16] |
周晓敏, 郑南山, 祁云, 等. 利用GPS-R遥感技术反演植被生物量[J]. 测绘通报, 2018(1): 129-132. |
| [17] |
王泽民, 刘智康, 安家春, 等. 基于GPS和北斗信噪比观测值的雪深反演及其误差分析[J]. 测绘学报, 2018, 47(1): 8-16. |
| [18] |
税广通, 郑南山, 周方平, 等. 一种GPS多路径反射信号的雪深反演[J]. 测绘科学, 2017, 42(10): 55-59. |
| [19] |
WANG X, ZHANG Q, ZHANG S. Water levels measured with SNR using wavelet decomposition and Lomb-Scargle periodogram[J]. GPS Solutions, 2018, 22(1): 22. DOI:10.1007/s10291-017-0684-8 |
| [20] |
张双成, 南阳, 李振宇, 等. GNSS-MR技术用于潮位变化监测分析[J]. 测绘学报, 2016, 45(9): 1042-1049. |



