2. 首都师范大学三维数据获取与应用重点实验室, 北京 100048;
3. 首都师范大学资源环境与旅游学院, 北京 100048
2. Key Lab of 3D Information Acquisition and Application, Capital Normal University, Beijing 100048, China;
3. College of Resources Environment and Tourism, Capital Normal University, Beijing 100048, China
传统移动测量系统(mobile mapping system,MMS)集成了导航系统,如全球导航卫星系统(GNSS)、惯性导航系统(INS)、遥感传感器(相机和三维激光扫描仪)及移动平台(如汽车、飞机等),能够获取目标点三维坐标信息[1]。这种系统的定位质量高度依赖于所使用的POS(position and orientation system)系统,然而高端的GPS/INS单元,尤其是惯性系统成本较高[2]。集成了全球导航卫星系统、加速度计、磁力计、相机等传感器[3]的智能手机,具备了成为移动测图设备的可能。将智能手机的定姿定位功能与影像量测技术相结合,可以提高移动测量设备的便携性,并大大降低成本。然而智能手机的传感器精度不高,降低了所获得的外方位元素的准确性[4]。针对这些问题,前人已经进行了一些相关的研究工作。
文献[5]研究了智能手机在特定环境中对于行人的姿态估计算法的精度。在建筑物中存在正常磁扰动的情况下,使用多个智能手机测试姿态估计技术,并提出了一种新的技术用于限制磁扰动带来的影响。文献[6]提出了一种基于视觉的方法,用于在室内环境中构建WiFi地图。通过视觉信息和惯性信息,在空间上恢复人们的轨迹,估计轨迹上的位置,并构造一个WiFi地图,实现了使用手机传感器进行室内定位。文献[7]介绍了一种基于智能手机的沿海监测技术,文中将手机获取的姿态数据与LPS(the ERDAS Leica photogrammetry suite)姿态数据进行对比,证明手机姿态数据能够精度满足需求。
本文提出使用基于LM(Levenberg Marquardt)算法的非线性最小二乘方法来修正初始的内、外方位元素及物方点坐标,以期克服目标点点位坐标计算值相对精度差的问题,从而实现较高精度的空间三维坐标的计算。
1 方法原理 1.1 相机标定受手机相机镜头的制造精度和组装工艺的影响,通过手机所拍影像存在畸变[8]。因此需要在获取影像前对手机相机进行标定。相机标定即是根据一组已知空间位置的点与其图像上的对应点求解相机参数的过程[9]。其最终目的是求出相机的内、外参数,以及畸变参数。本文采用了文献[10]提出的相机标定方法,通过坐标系的转换获得相机的内参数矩阵。
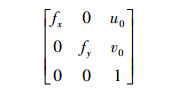 (1)
(1) 式中,fx、fy为焦距,一般情况下,二者相等;(u0, v0)为主点相对于成像平面的坐标。
理想图像的像素坐标与实际图像的像素坐标之间的关系为
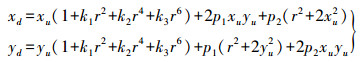 (2)
(2) 式中,(xu, yu)为畸变点在成像仪上的原始位置;r为该点距离成像仪中心的距离;(xd, yd)为校正后的新位置;k1、k2、k3为径向畸变参数;p1、p2为切向畸变参数。其中r可表示为
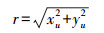 (3)
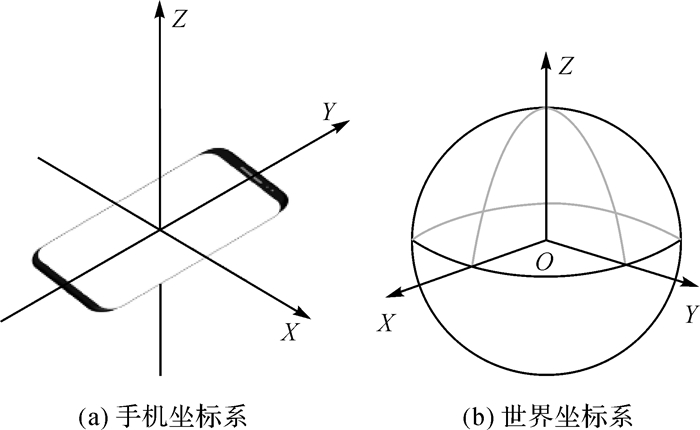
(3) 在安卓手机中,加速度计、磁场计等传感器的输出结果均以手机局部坐标系为参考基准,而手机坐标系是以手机屏幕为基准定义的一种相对坐标系[11]。当一个设备被放在其默认的方向上时,X轴水平指向右,Y轴垂直向上,Z轴指向屏幕正面之外,如图 1(a)所示。由于在手机运动过程中,手机坐标系不断变化。为此,在实际计算中,需要将手机坐标系转换到统一的世界坐标系中,如图 1(b)所示。
|
| 图 1 两种坐标系 |
惯性坐标系可以看作是手机坐标系与世界坐标系之间的中间状态,其原点与手机坐标系的原点重合,坐标轴与世界坐标系的坐标轴平行[12]。因此,本文利用惯性坐标系来完成手机局部坐标系与世界坐标系之间的转换。
1.2.2 外方位元素的获取确定影像或摄影光束在摄影瞬间的空间位置和姿态的参数,称为外方位元素。其中线元素用于描述摄影中心S相对于物方空间坐标系的位置(XS, YS, ZS)[13]。手机方向传感器可以提供当前的手机姿态数据,分别为航向角、俯仰角、翻滚角(a,p,r)。由手机姿态角获得旋转矩阵的方法如下:
绕z轴旋转
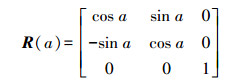 (4)
(4) 绕x轴旋转
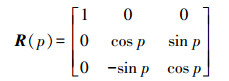 (5)
(5) 绕y轴旋转
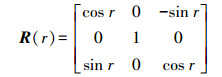 (6)
(6) 将这3个基本旋转序列以适当方式组合,可得到两个坐标系之间的旋转矩阵,本文以常用的z-x-y序列旋转,即
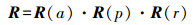 (7)
(7) 得手机坐标系到惯性坐标系的旋转关系为
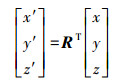 (8)
(8) 式中, (x′, y′, z′)为惯性坐标系下点的三维坐标;(x, y, z)为手机坐标系下点的三维坐标。
1.3 同名点匹配SURF算法对物体的旋转、光照等情况有较好的稳健性,且较SIFT算法而言计算速度更快[14]。本文使用SURF进行特征点提取,并通过FLANN(fast library for approximate nearest neighbors)进行匹配。
FLANN实现了一系列查找算法,还包含了一种自动选取最快算法的机制[15]。本文使用FLANN进行特征点匹配,并利用RANSAC(random sample consensus)约束实现粗差剔除。
RANSAC算法通过迭代计算坐标转换误差和异常值,直至获得具有最大内点数的单应矩阵[16]。在去除异常值之后,可以改善图像匹配的性能。
如图 2所示,在使用RANSAC算法进行粗差剔除后,错误的匹配点明显减少,证明该方法效果良好。

|
| 图 2 |
目标点的三维坐标初始值由立体像对空间前方交会获取。立体像对的空间前方交会是指利用左右两张像片的同名像点的像平面坐标和像片的内、外方位元素来确定该点的物方空间坐标的方法。使用立体像对上的同名像点,就能得到两条同名射线在空间的方向,这两条射线在空间一定相交,其相交处必然是该地面点的空间位置[13]。根据手机获得的位置姿态数据,以及同名像点的影像坐标,通过空间前方交会计算像点的物方空间坐标,作为光束法平差的初始值。
1.4.2 光束法平差光束法平差的目的是找到重投影误差最小化的三维点位置和相机参数。该优化问题通常被称为非线性最小二乘问题[17]。
在光束法平差中,相机模型可表示为
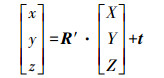 (9)
(9) 式中,(x, y, z)为相机坐标系坐标;(X, Y, Z)为世界坐标系坐标;R′为世界坐标系旋转到相机坐标系的罗德里格斯矢量; t为平移量,即摄影中心的世界坐标。
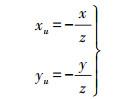 (10)
(10) 式中,(xu, yu)为畸变点在成像仪上的原始位置。由此可得
 (11)
(11) 式中,(xpredicted, ypredictied)为根据已知同名点的世界坐标值计算得到的图像坐标系坐标值;f为焦距;r为畸变点距离成像仪中心的距离;k1、k2为径向畸变参数。而在摄影测量中,其相机模型与光束法平差刚好相反,可描述为
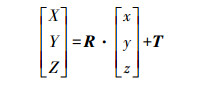 (12)
(12) 其中
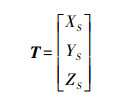 (13)
(13) 式中,T为像片摄影中心的世界坐标。
因此可以得到摄影测量中坐标系转换的参数与光束法平差中参数的关系为
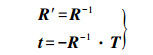 (14)
(14) 光束法平差的实质是计算残差,并使残差最小。残差公式为
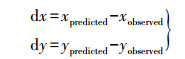 (15)
(15) 式中,(xobserved, yobserved)为1.3节中得到的同名点图像坐标。
LM算法是求解非线性最小二乘问题最常用的算法[18],也是光束法平差的首选算法。LM算法保证了每次迭代都是下降的,并且可以快速收敛。
2 试验分析由于手机内置传感器受磁场和手机电子设备的干扰,在采集数据前,应尽量远离其他电子设备,以保证获取的数据尽量精确;同时选取特征点较多且清晰的地方进行数据采集。
2.1 相机标定表 1、表 2为通过标定棋盘格对智能手机相机的标定结果,所使用的智能手机为Samsung Galaxy S8。
| 机型 | k1 | k2 | k3 | p1 |
| Samsung Galaxy S8 | 0.133 009 995 | -0.228 390 907 | -0.002 825 789 6 | -0.000 436 608 06 |
本次试验区为北京市大兴区亦庄开发区,地形开阔,无大型建筑物遮挡,通视效果好。本次图像采集时间为16:00:00,拍摄时光线良好,拍摄像片清晰。图 3为立体像对中的一组。

|
| 图 3 一组手机获取的影像 |
通过智能手机获取的像片位置姿态信息见表 3。
| 照片编号 | 方向 | 线元素/m | 姿态 | 角元素/(°) |
| 1 | X | 440 3272.154 944 | 航向角 | 50.363 514 |
| Y | 458 278.097 015 | 俯仰角 | -38.975 674 | |
| Z | 21.492 | 翻滚角 | -21.059 156 | |
| 2 | X | 4 403 274.376 600 | 航向角 | 20.033 936 |
| Y | 458 276.221 487 | 俯仰角 | -52.697 66 | |
| Z | 22.685 | 翻滚角 | -26.984 594 |
根据获得的试验数据,设定合适的阈值,得到一组剔除粗差后的同名点的图像坐标,结果如图 4所示。

|
| 图 4 |
通过空间前方交会计算出一组物方点坐标,由于手机定位在Z方向上误差较大,根据实际情况可知两个摄影中心实际高程差很小,因此在本次试验中,将两个摄影中心的世界坐标的Z值均取21.492 m。通过全站仪测量其中13个点的世界坐标作为真实值,表 4给出了这13个点的真实坐标、优化前坐标(即空间前方交会得到的物方坐标)及优化后的坐标(即经过光束法平差后的物方坐标)。
| m | ||||
| 点号 | 方向 | 真实坐标 | 优化前坐标 | 优化后坐标 |
| 1 | X | 4 403 265.75 | 4 403 257.429 364 | 4 403 269.845 289 |
| Y | 458 274.04 | 458 284.759 211 | 458 277.909 621 | |
| Z | 25.54 | 41.496 120 | 24.375 319 | |
| 2 | X | 4 403 265.76 | 4 403 257.253 763 | 4 403 269.848 581 |
| Y | 458 274.05 | 458 285.247 685 | 458 277.913 124 | |
| Z | 24.78 | 38.646 863 | 24.360 008 | |
| 3 | X | 4 403 263.12 | 4 403 264.939 498 | 4 403 269.847 859 |
| Y | 458 273.03 | 458 278.193 366 | 458 277.877 082 | |
| Z | 24.76 | 27.467 216 | 24.330 520 | |
| 4 | X | 4 403 264.34 | 4 403 262.822 299 | 4 403 269.846 180 |
| Y | 458 273.74 | 458 280.431 839 | 458 277.901 790 | |
| Z | 24.20 | 29.358 845 | 24.336 216 | |
| 5 | X | 4403 265.75 | 4 403 264.204 062 | 4 403 270.294 834 |
| Y | 458 274.04 | 458 282.377887 | 458 277.849 412 | |
| Z | 22.65 | 27.241 573 | 23.848 469 | |
| 6 | X | 4 403 265.78 | 4 403 269.169 687 | 4 403 270.284 368 |
| Y | 458 274.02 | 458 279.780 809 | 458 277.852 802 | |
| Z | 21.35 | 23.100 631 | 23.846 495 | |
| 7 | X | 4403 263.09 | 4 403 266.583 136 | 4 403 269.862 463 |
| Y | 458 273.01 | 458 278.777 232 | 458 277.884 653 | |
| Z | 22.64 | 24.333 092 | 24.281 533 | |
| 8 | X | 4 403 265.00 | 4 403 261.898 369 | 4 403 269.844 429 |
| Y | 458 273.75 | 458 281.289 543 | 458 277.904 459 | |
| Z | 25.05 | 32.818 008 | 24.361 403 | |
| 9 | X | 4 403 262.49 | 4 403 266.544 326 | 4 403 269.858 938 |
| Y | 458 272.78 | 458 278.360 363 | 458 277.878 340 | |
| Z | 22.66 | 24.151 168 | 24.281 879 | |
| 10 | X | 4403 262.38 | 4 403 266.255 507 | 4 403 269.856 091 |
| Y | 458 272.75 | 458 278.244 681 | 458 277.876 851 | |
| Z | 22.85 | 24.404 478 | 24.286 832 | |
| 11 | X | 4 403 262.81 | 4 403 266.148 211 | 4 403 269.856 094 |
| Y | 458 272.90 | 458 278.529 424 | 458 277.881 173 | |
| Z | 22.95 | 24.690 520 | 24.290 317 | |
| 12 | X | 4 403 262.77 | 4 403 266.727 003 | 4 403 269.861 823 |
| Y | 458 272.90 | 458 278.560 468 | 458 277.881 346 | |
| Z | 22.55 | 24.088 121 | 24.279 196 | |
| 13 | X | 4 403 263.50 | 4 403 266.701 054 | 4 403 269.868 538 |
| Y | 458 273.18 | 458 279.087 451 | 458 277.889 071 | |
| Z | 22.56 | 24.363 086 | 24.276 994 | |
由于光束法平差是一种整体优化,因此会有个别点的坐标值反而与真值相差更大,但总体上,优化后精度有明显提高。
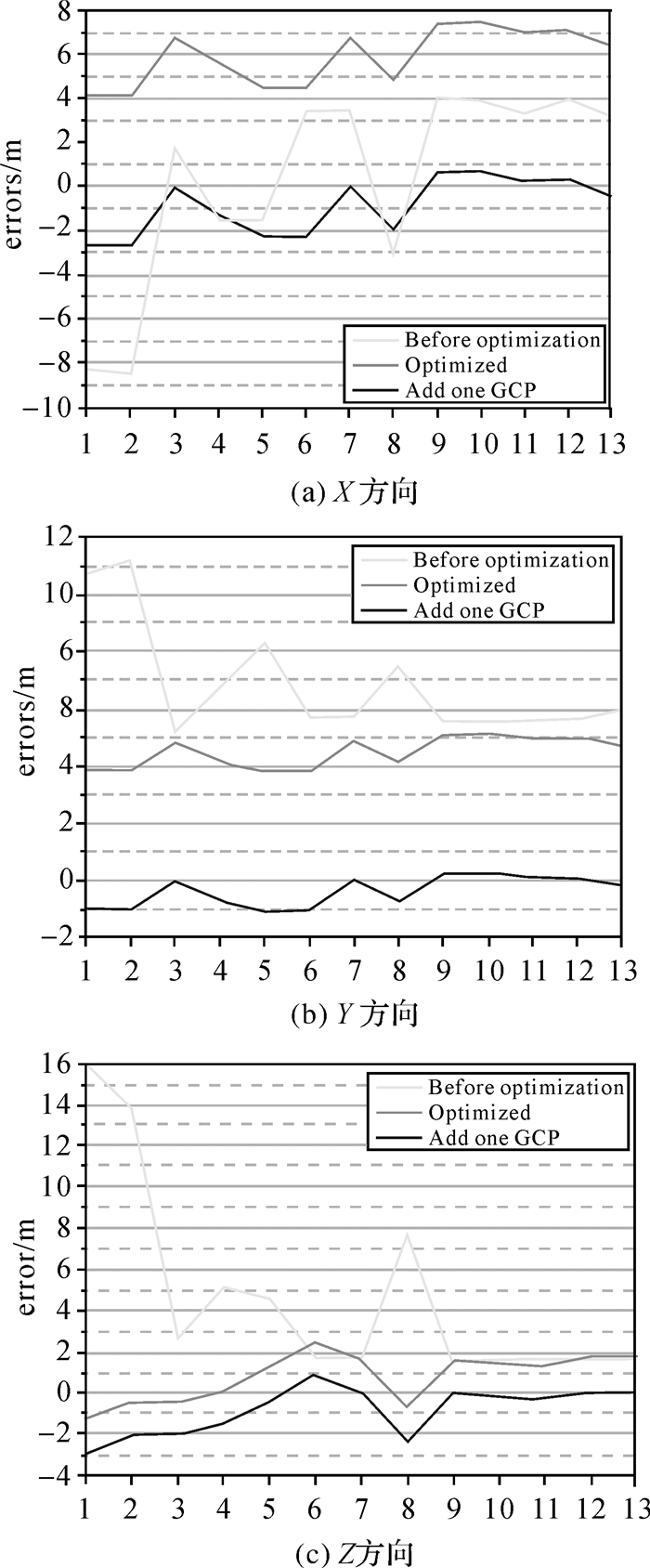
2.3.3 精度评价为了验证本文方法的精度,分别将优化前与优化后的物方坐标与真实值进行对比,得到各轴坐标的差值,如图 5所示。
|
| 图 5 X、Y、Z 3个方向差值对比 |
图 5中黑色线为空间前方交会结果与真值的差值,可以看出在X、Y、Z 3个方向上,差值起伏较大,且没有规律。深灰色折线为优化后结果与真实值的差值,可以看出优化后差值趋于平稳,且稳定在横轴的一侧或横轴附近。其中,X轴的折线虽出现在优化前折线的上方,但根据X、Y、Z 3个方向上的结果来看,物方点的相对位置较优化前有了很大的改善。图中浅灰色折线为加入一个控制点(GCP)后的差值,即把所有的物方点作整体的平移,本文选择7号点为控制点,经过平移后,可以看出X、Y、Z 3个方向的误差均在零线附近。
标准差能够表示数据的离散程度,RSME代表了观测值与真实值之间的偏差。为了进一步验证本文方法的精度,对优化后的结果增加1个控制点并统计3个坐标轴的标准差和RMSE,同时与优化前后进行对比。从表 5中可以看出,优化后3个坐标轴的离散程度明显减小,说明误差趋于稳定,相对位置精度明显提高。同时,虽然优化后X方向的RSME增加了,但是X、Y、Z整体的偏差减小。此外,加入1个控制点后,也使RSME明显减小,提高了绝对精度。表 6给出了优化前、优化后及加1个控制点后的最大误差与最小误差。可以看出,优化后点位误差明显减小,加入1个控制点后点位误差进一步减小。
| m | ||||
| 项目 | 方向 | 优化前 | 优化后 | 加1个GCP |
| 标准差 | X | 4.386 118 | 1.259 680 | 1.259 680 |
| Y | 2.021 152 | 0.538 112 | 0.538 112 | |
| Z | 4.718 183 | 1.120 963 | 1.120 963 | |
| RMSE | X | 4.397 643 | 6.013 078 | 1.543 989 |
| Y | 7.149 529 | 4.515 061 | 0.647 176 | |
| Z | 6.687 948 | 1.386 837 | 1.391 816 | |
由于智能手机的不断发展,使用手机作为数据采集设备,价格低廉且方便快捷,本文提出了一种基于智能手机的可移动测量方法。该方法通过获取手机影像及传感器数据,运用摄影测量的方式获取影像目标点的三维坐标信息,通过光束法平差实现整体优化,使用LM算法实现快速收敛,从而得到相对准确的点位坐标。本文方法实现了手机的可移动测量,使数据采集的过程变得非常简单。通过试验过程与最终的数据结果分析,证明了该方法可以获得较好的点位精度,并具备实际的可行性。
| [1] |
ELLUM C, ELSHEIMY N. Land-based mobile mapping systems[J]. Photogrammetric Engineering and Remote Sensing, 2002, 68(1): 13-17. |
| [2] |
RAU J Y, HABIB A F, KERSTING A P, et al. Direct sensor orientation of a land-based mobile mapping system[J]. Sensors, 2011, 11(7): 7243-7261. DOI:10.3390/s110707243 |
| [3] |
尹邦杰, 黄晓莹. 浅析Android手机传感器机制及应用设计举例[J]. 计算机光盘软件与应用, 2013(5): 148-148. |
| [4] |
陈龙彪, 李石坚, 潘纲. 智能手机, 普适感知与应用[J]. 计算机学报, 2015, 38(2): 423-438. |
| [5] |
THIBAUD M, GENEVES P, FOURATI H, et al. On attitude estimation with smartphones[C]//Proceedings of 2017 IEEE International Conference on Pervasive Computing and Communications. Kona: IEEE, 2017: 267-275.
|
| [6] |
LIU T, ZHANG X, LI Q, et al. A visual-based approach for indoor radio map construction using smartphones[J]. Sensors, 2017, 17(8): 1790. DOI:10.3390/s17081790 |
| [7] |
KIM J, LEE S, AHN H, et al. Accuracy evaluation of a smartphone-based technology for coastal monitoring[J]. Measurement, 2013, 46(1): 233-248. DOI:10.1016/j.measurement.2012.06.010 |
| [8] |
DRUMMOND J. Manual of photogrammetry[J]. Photogram-metric Record, 2010, 20(112): 390-392. |
| [9] |
LI H, YANG D H, ZHAI C. Research on the pose measurement of a 6-DOF platform using a single camera[J]. Optical Technique, 2010, 36(3): 344-349. |
| [10] |
ZHANG Z Y. A flexible new technique for camera calibration[M].[S.l.]: IEEE Computer Society, 2000.
|
| [11] |
张勇, 夏家莉, 陈滨. Google Android开发技术[M]. 西安: 西安电子科技大学出版社, 2011: 124-127.
|
| [12] |
赵宏, 郭立渌. 手机内置加速度传感器数据的空间坐标转换算法[J]. 计算机应用, 2016, 36(2): 301-306. |
| [13] |
张剑清, 潘励, 王树根. 摄影测量学[M]. 2版. 武汉: 武汉大学出版社, 2009: 64-65.
|
| [14] |
BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF)[J]. Computer Vision and Image Understanding, 2008, 110(3): 346-359. DOI:10.1016/j.cviu.2007.09.014 |
| [15] |
MUJA M, LOWE D G. Fast approximate nearest neighbors with automatic algorithm configuration[C]//Proceedings of the 4th International Conference on Computer Vision Theory and Application. Lisboa: DBLP, 2009.
|
| [16] |
FISCHLER M A, BOLLES R C. A paradigm for model fitting with applications to image analysis and automated cartography[J]. Communication of the ACM, 1981, 24(6): 381-395. DOI:10.1145/358669.358692 |
| [17] |
AGARWAL S, SNAVELY N, SEITZ S M, et al. Bundle adjustment in the large[C]//Proceedings of European Conference on Computer Vision.[S.l.]: Springer-Verlag, 2010: 29-42.
|
| [18] |
NOCEDAL J, WRIGHT S J. Numerical optimization[M].[S.l.]: Springer, 1999.
|


