2. 中国测绘科学研究院, 北京 100036
2. Chinese Academy of Surveying and Mapping, Beijing 100036, China
通行时间隐含道路交通状况信息,是居民出行关注的重要问题。通行时间估计同时也被广泛应用于出行路线规划、交通状况监控[1]、出行辅助决策、车辆调度[2]等各大基于位置的服务。浮动车轨迹覆盖范围广,可持续大量获取,是交通状态挖掘和通行时间估计的典型数据源[3-7]。
基于浮动车历史轨迹估计路径通行时间,核心思想是用一组通过指定路径的历史轨迹的通行时间估计该路径的通行时间。受数据时空分布特征影响,在指定时隙和路径通常很难找到一组完整的历史轨迹,因此需要对路径进行剖分。现有研究包括两种典型方法:基于路网节点划分和基于规则格网划分。文献[8]基于支持向量回归模型,通过统计历史时段车辆穿过道路两端所用时间估计了路径通行时间。文献[9]采用规则格网划分地理空间,基于稀疏轨迹结合POI兴趣点、天气状况等信息,通过动态规划寻找最佳级联和构建三阶张量模型估计了路径通行时间[9]。然而这些研究并未考虑海量数据的高效管理,算法完成多在本地计算机实现,虽然规则格网划分较路网节点划分具有更高的计算效率,但轨迹数据量巨大时计算机计算过程仍具有较大压力。
本文从轨迹数据和相关基础数据高效一体化管理的角度研究路径通行时间,依托于Apache平台Cassandra数据库设计数据索引策略和高效检索算法,利用分布式数据库存储及索引策略降低通行时间估计的计算压力;基于Google S2[10]索引格网单元划分轨迹段和路段,挖掘历史轨迹在Cell中的停留时间,构建模式知识库;将复杂路线分解为一组路段模式,利用历史时隙相似路段模式估计车辆通行时间。
1 数据清洗及模式库构建 1.1 轨迹数据清洗轨迹数据清洗包括以下3部分:
(1) 异常点及运动状态提取。设置时间阈值φT为轨迹最大采样间隔,当前轨迹点与前一点时间间隔为Δt、空间距离为Δs,空间阈值φS=120Δt。当Δt>φT时,当前轨迹点作为新的轨迹段的起点;当Δt≤φT且ΔS>φS时,该点作为异常点剔除。当ΔS < 5 m时,轨迹运动状态为静止,标记State=1;否则,标记State=0。
(2) 滤波[11]。分别将轨迹数据坐标值和运动状态作为输入值进行中值滤波,消除轨迹点噪声及异常运动状态判断。设置窗口大小m=5,将窗口内中心点的值Yi用窗口内各点的中值代替。
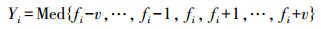 (1)
(1) 式中, i∈N;v=(m-1)/2。
设置时间阈值为30 min,当一组轨迹点在连续超过30 min的时段内State=1时,当前该组连续状态为1的轨迹点的中心点为静止点,对轨迹进行切分,产生新的轨迹段。用轨迹ID标识切分后的轨迹段,轨迹ID的编码方式为“车辆编号@轨迹段编号”。
(3) 地图匹配。采用隐马尔可夫模型[12-13]实现地图匹配,获取轨迹点对应的路段。
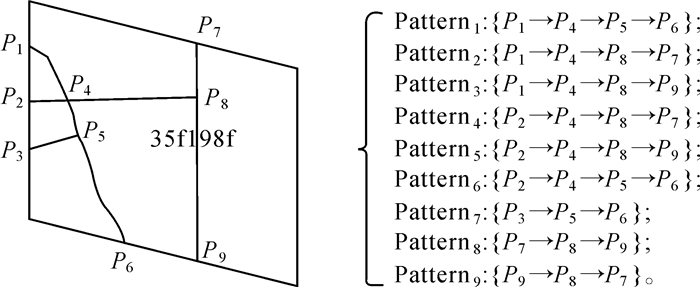
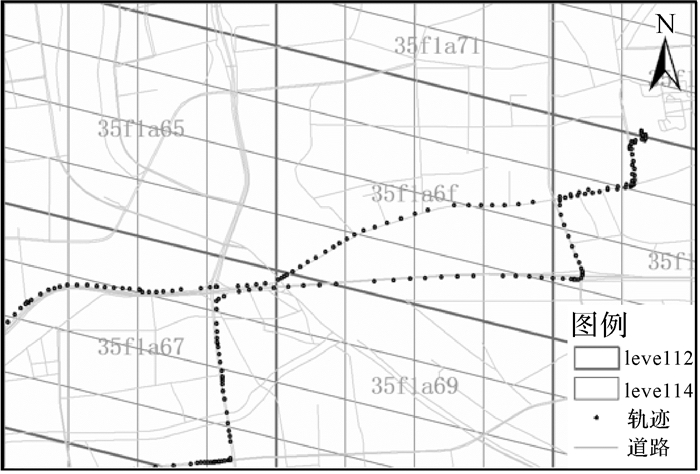
1.2 模式库构建基于Google S2索引生成的地理格网对路网进行分割,单个Cell中的路网拓扑重构后获得Cell所对应的路段模式(Pattern)。以Cell为单位编码组织路段模式,构建模式知识库。知识库中每条路段模式的历史通行时间由一系列历史轨迹综合计算获得。图 1为空间索引编码为“35f198f”的Cell中的全部路段模式示例(部分路段为单行道)。
|
| 图 1 Cell中路段模式 |
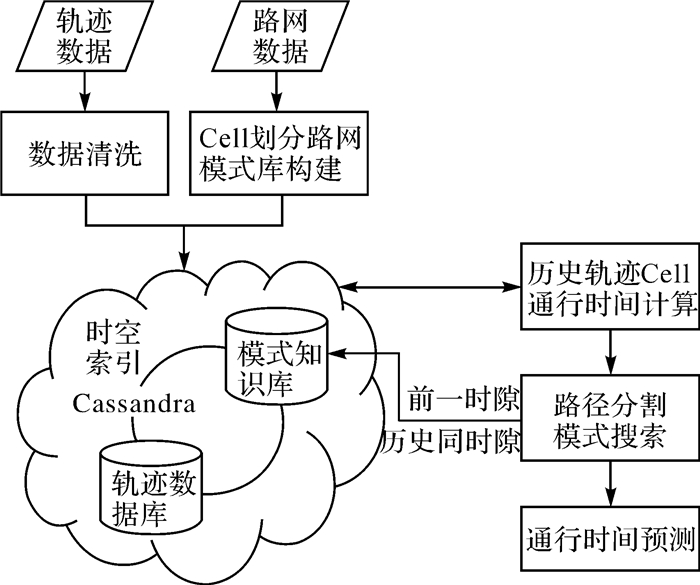
本文通行时间估计模型的关键为时空索引构建和基于索引的轨迹及路网划分,模型如图 2所示。
|
| 图 2 通行时间估计模型 |
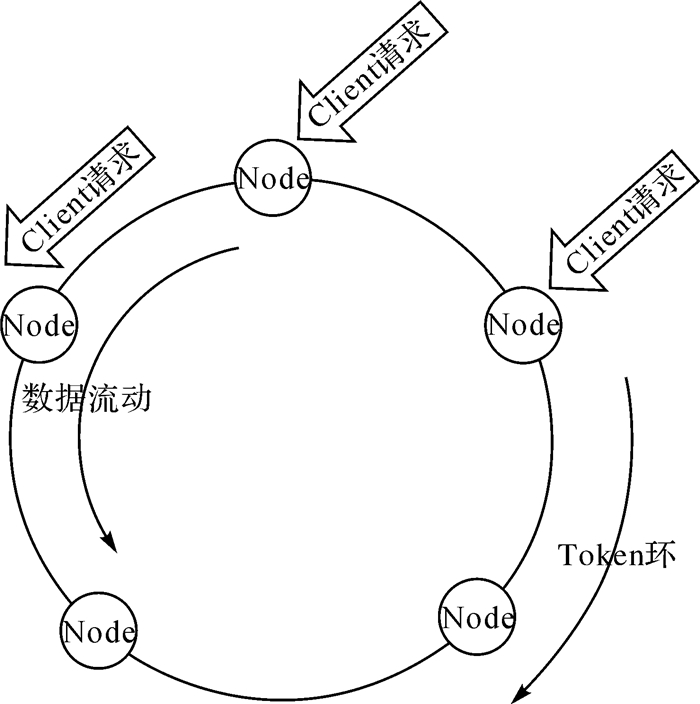
非关系型Cassandra数据库具有较快的读写性能,能够高效管理复杂的高动态高实时轨迹数据。其P2P去中心化架构及一致性Hash环保证了数据的安全性、最终一致性和负载均衡性。Cassandra数据库为Key-Value数据库,由分区键和排序键组成Row Key,通过Hash值确定要素在分布式Hash环中存储的位置,具有相同分区键的数据存储在同一个节点上[14-15],工作原理如图 3所示。本文采用时空划分的方式通过设计分区键和排序键构建时空索引。
|
| 图 3 Cassandra工作模型 |
轨迹和路网数据空间划分采用Google S2索引,该索引提供了一种分级的全球格网划分和编码方案。采用S2算法对轨迹数据和路网数据进行编码,采用12级地理格网编码索引轨迹数据,14级地理格网编码索引路网数据。12级的地理格网面积约为5.07 km2,索引次数引发的时间复杂度和去除冗余查询结果产生的时间消耗相对平衡,具有较好的查询性能。14级地理格网覆盖面积约为0.32 km2,格网内路网结构简单,轨迹分布适中,能够减少不确定性因素,保证通行时间估计的效率及准确性。图 4为分级格网索引示意图。轨迹数据存储表结构见表 1。数据时间以1 h为间隔进行划分,组合空间和时间编码为分区键。将清洗和路网匹配后的轨迹数据按表 1的结构构建索引存储。模式知识库存储结构见表 2。
|
| 图 4 分级空间索引 |
通行时间估计算法通过计算历史通行时间完善路径模式知识库,利用知识库实现任意时段任意路径的通行时间估计。
生成覆盖研究区域和历史时段的时空索引值检索全部轨迹数据。以轨迹ID为单位按时间排序组织轨迹数据。地理格网将每一条轨迹划分为一组轨迹段,Cell中的每一个轨迹段对应模式库中的一个路段模式。轨迹段时间维度以小时为单位进行划分。每个时段Cell中路段模式的通行时间由与该路段模式对应的一组轨迹中对应时段的数据综合计算获得。受出行特征影响,对工作日和休息日分别进行计算。匹配Cell中轨迹段和路段模式的算法如下:①获取当前轨迹段Tri的最小外包矩形MBRTri;②检索数据库获取当前Cell中的全部路段模式,计算每个模式的最小外包矩形MBRPTj,若MBRTri≥MBRPTj,将该模式存入候选结果集合Cand1;③对Cand1中的路段模式作缓冲区Buffer,若Buffer包含当前轨迹段,且长度差小于阈值,则将该模式存入候选结果集Cand2;④若Cand2为空,求取Cell中与当前轨迹段最相似的路段模式为当前轨迹段对应的Pattern,否则求取Cand2中与当前轨迹段最相似的路段模式作为当前轨迹段对应的Pattern。定义轨迹和路段模式的相似距离函数如下
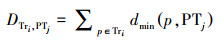 (2)
(2) 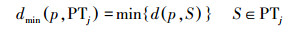 (3)
(3) 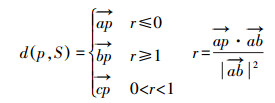 (4)
(4) 式中,p为轨迹Tri上的轨迹点;PTj为Cell中的一条路段模式;dmin(p, PTj)为轨迹段Tri上的轨迹点p与某一路段模式PTj的最短距离。PTj由一组直线段S组成,a、b表示S的端点,点c为轨迹点p在直线段S上的投影。轨迹段和模式的相似距离DTri, PTj为轨迹段上全部轨迹点与PTj的最短距离和,其值越小相似性越高。
匹配Cell中轨迹段和模式后,模式知识库中每一条Pattern在特定的时隙均有一组轨迹作为其训练样本。计算该组历史轨迹在Cell中的停留时间,作为车辆穿过该Pattern所需的时间。无历史轨迹经过的路段采用限速计算其通行时间,标识该路段的通行时间为理想状态通行时间。本文上节中的索引具有实时性,能够实现模式知识库通行时间的迅速写入和更新。
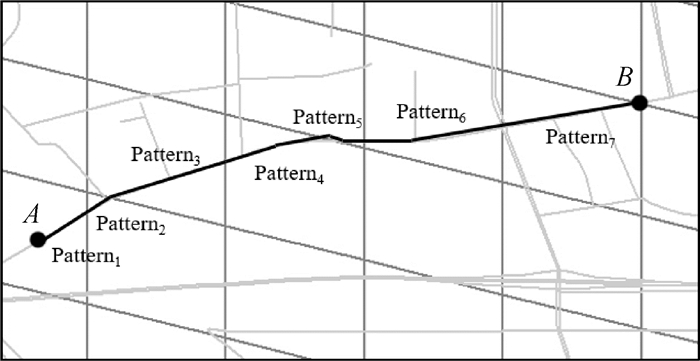
由模式知识库中模式的通行时间估计车辆从某一时刻起通过指定路径R所需的时间算法如下:①生成覆盖路径R的地理格网编码和时隙编码集合;②地理格网将R划分为一组落在Cell中的路段,每条路段对应一条Pattern,如图 5两点之间路径R为一组路段Pattern的集合,R={Pattern1, Pattern2, …, Patternn},路径R的预测通行时间为集合中全部Pattern通行时间之和;③组合空间编码和时间编码为分区键,检索知识库;④搜索知识库中历史同时隙与Patterni对应的路段模式,获取历史通行时间;⑤若Patterni在历史同时段无车辆通过,搜索当前Cell中道路等级与当前路段相似的距离最近的路段模式;⑥若仍无历史轨迹通过,以理想状态计算。
|
| 图 5 路径模式集合 |
采用北京市10 000辆出租车一周内采集的约1500万个轨迹点及OpenStreetMap开源的路网数据完成试验。清洗和匹配全部轨迹数据,筛选出采样间隔小于等于30 s、时间跨度在周一至周五内的车辆轨迹,按照上文的索引策略入库。分割重构路网数据构建模式知识库。选择周一至周四4 d的历史轨迹作为计算模式知识库中每一个模式在1 d 24个时段各自通行时间的样本。使用周五的轨迹数据验证通行时间估计结果的准确性。
采用平均绝对误差(MAE)和平均相对误差(MRE)评估估计结果的准确性。计算方法见式(5)—式(6),ti为第i条路径的实际通行时间,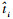
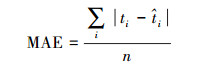 (5)
(5) 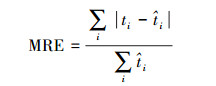 (6)
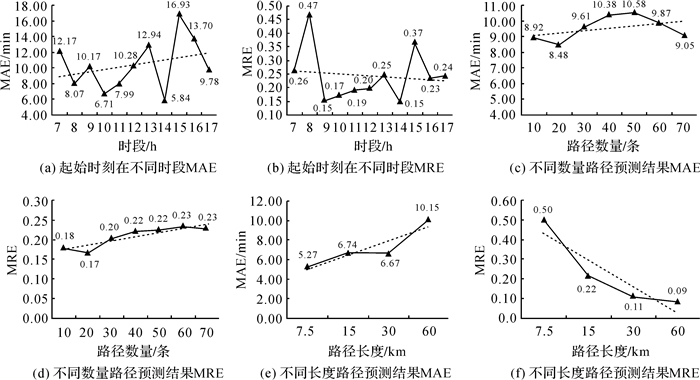
(6) 随机抽取100条不同时段不同长度的轨迹段,将轨迹的起始时刻作为时间估计的起始时刻,轨迹经过的路径作为时间估计的路径,轨迹的实际通行时间作为真实值与估计结果对照,计算MAE和MRE。图 6(a)和图 6(b)为轨迹起始时刻落在7~17 h之间的不同时段时估计结果的MAE和MRE。结果显示,路径通行时间估计的整体平均绝对误差在10 min左右,非高峰时段误差相对较小,高峰时段受交通状况不确定性影响误差增大;平均相对误差趋近0.20,具有一定的整体精度。图 6(c)和图 6(d)随着估计路径数量的增加,MAE和MRE稳定在10 min和0.20。随机抽取平均长度分别为7.5、15、30和60 km的4组轨迹,每组50条,估计通行时间并计算MAE和MRE。图 6(e)和图 6(f)随着路径长度的增大,MAE小幅度增加但仍稳定在10 min左右,MRE大幅度减小。因此,对于较长的复杂路线,本文方法具有较高的估计精度。
|
| 图 6 通行时间估计结果准确性评估 |
表 3统计了本文通行时间估计模型的方法耗时。利用10 000辆出租车周一至周四的历史轨迹构建知识库的所需时间为13.68 min。随着路径长度的增加,需要从知识库中检索的路段模式也增加,估计通行时间的耗时小幅度增加。长度在30 km内的路径,通行时间估计平均耗时稳定在3 s内。因此,对估算较长路径上车辆的通行时间,本文方法具有较高的估算效率。
| 方法 | 路径长度/km | 耗时 |
| 检索历史轨迹,构建知识库 | — | 13.68 min |
| 检索知识库,估计通行时间 | 7.5 | 0.32 s |
| 15 | 0.80 s | |
| 30 | 2.51 s | |
| 60 | 4.01 s |
通行时间估计结果准确性评估及方法效率评估表明:空间维度引入地理格网、组合空间和时间信息构建时空复合索引,能够减轻海量历史轨迹的管理和计算压力;地理格网划分轨迹和路网,将全局通行状况的挖掘转换为局部状况的分析和累积,能够最大化地挖掘历史轨迹的通行状况,提高较长路径车辆通行时间估计的准确性和效率。
4 结语本文提出了一种基于地理格网的复杂路线车辆通行时间估计方法,利用地理格网划分历史轨迹和路网挖掘历史交通状态,较好地完成了指定路径车辆通行时间估计,通过索引构建和相似轨迹搜索算法提高了数据检索效率。时间估计模型依托于轨迹数据和基础数据的高效一体化管理,减轻了计算机计算压力。此外,路径通行时间通常受各种复杂因素的影响,今后的研究将综合考虑各种不确定性因素,完善本文提出的通行时间估计模型,在轨迹数据高效管理的基础上挖掘数据的其他价值。
| [1] |
CHAWLA S, ZHENG Y, HU J. Inferring the root cause in road traffic anomalies[C]//Proceedings of International Conference on Data Mining.[S.l.]: IEEE, 2013: 141-150.
|
| [2] |
YUAN N J, ZHENG Y, ZHANG L, et al. T-finder:a recommender system for finding passengers and vacant taxis[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(10): 2390-2403. DOI:10.1109/TKDE.2012.153 |
| [3] |
王晓蒙, 彭玲, 池天河. 基于稀疏浮动车数据的城市路网交通流速度估计[J]. 测绘学报, 2016, 45(7): 866-873. |
| [4] |
董岳, 张发明. 利用低频浮动车交叉口运行状态的单车路段行程时间估计[J]. 测绘地理信息, 2018(3): 28-32. |
| [5] |
涂丽佳.基于轨迹数据的长距离路径通行时间估计问题[D].哈尔滨: 哈尔滨工业大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10213-1017739642.htm
|
| [6] |
刘扬.基于网格模型的城市交通运行状态识别和行程时间预测方法研究[D].北京: 北京交通大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10004-1018144557.htm
|
| [7] |
ZHANG X, HASAN S, UKKUSURI S V, et al. Urban link travel time estimation using large-scale taxi data with partial information[J]. Transportation Research Part C, 2013, 33(4): 37-49. |
| [8] |
WU C H, HO J M, LEE D T. Travel-time prediction with support vector regression[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(4): 276-281. DOI:10.1109/TITS.2004.837813 |
| [9] |
WANG Y, ZHENG Y, XUE Y. Travel time estimation of a path using sparse trajectories[C]//Proceedings of the 20th SIGKDD Conference on Knowledge Discovery and Data Mining.[S.l.]: ACM, 2014: 25-34.
|
| [10] |
CHRISTIAN S P. Google's S2, geometry on the sphere, cells and Hilbert curve[EB/OL]. 2015-08-14[2018-09-18]. http://blog.christianperone.com/2015/08/googles-s2-geometry-on-the-sphere-cells-and-hilbert-curve/.
|
| [11] |
高强, 张凤荔, 王瑞锦, 等. 轨迹大数据:数据处理关键技术研究综述[J]. 软件学报, 2017, 28(4): 959-992. |
| [12] |
NEWSON P, KRUMM J. Hidden Markov map matching through noise and sparseness[C]//Proceedings of ACM Sigspatial International Conference on Advances in Geographic Information Systems.[S.l.]: ACM, 2009: 336-343.
|
| [13] |
GOH C Y, DAUWELS J, MITROVIC N, et al. Online map-matching based on Hidden Markov model for real-time traffic sensing applications[C]//Proceedings of International IEEE Conference on Intelligent Transportation Systems. Anchorage: IEEE, 2012: 776-781.
|
| [14] |
BRAHIM M B, DRIRA W, FILALI F, et al. Spatial data extension for Cassandra NoSQL database[J]. Journal of Big Data, 2016, 3(1): 1-16. |
| [15] |
MISHRA V. Beginning Apache Cassandra development[M].[S.l.]:Apress, 2014.
|


