单幅影像通常无法覆盖航摄测区范围,因此大范围DOM的生产需要对多幅影像进行镶嵌处理[1]。镶嵌线的自动生成作为影像镶嵌中的关键步骤,已经成为计算机视觉、摄影测量与遥感领域的研究热点之一[2-4]。现有的镶嵌线自动提取方法大多只关注相邻两幅影像的拼接,处理多幅影像时,将当前两幅影像的镶嵌结果与剩余影像中的下一幅影像进行镶嵌,依此类推直到所有影像镶嵌完毕。这种处理模式严重依赖镶嵌过程,处理效率较低[5-6]。随着高精度、高重叠度与高分辨率遥感数据的不断涌现,研究基于全局的镶嵌网络自动生成,确定每幅影像的有效镶嵌区域成为提升大范围、海量影像镶嵌处理效率的关键[6-7]。
文献[8]提出了将单独镶嵌线连接生成镶嵌网络的方法,该方法需要记录测区航带信息,适用性有限。文献[9]研究了利用Voronoi图生成镶嵌网络,但其不能保证生成的镶嵌线一定在相邻DOM影像的重叠区域内,从而导致镶嵌结果可能存在未被有效数据覆盖的区域。文献[7, 10]提出了顾及重叠的面Voronoi图初始镶嵌线网络生成方法,该方法具有与输入影像顺序无关、无中间结果等优点,但是对处理单片纠正后有效范围呈不规则多边形的正射影像比较复杂。文献[11]改进了文献[7]提出的顾及重叠的面Voronoi图方法,通过局部搜索将镶嵌网络顶点调整到最优位置,但受限于搜索范围,顶点仍然可能位于建筑和树木等障碍区域。
结合DOM实际镶嵌生产需求,本文提出基于Voronoi图的正射影像镶嵌网络生成及优化方法。通过构建Voronoi图生成初始镶嵌网络,然后结合数字表面模型(digital surface model,DSM)数据对镶嵌网络顶点进行动态调整以避免镶嵌结果出现无数据区域,并使顶点避开建筑、树木等区域,以便使用已有的各类镶嵌线自动提取方法对镶嵌网络进一步调整优化。
1 基于Voronoi图的初始镶嵌网络生成 1.1 Voronoi图介绍Voronoi图是计算几何领域关于空间划分的基础数据结构,它是一组由连接相邻两点直线的垂直平分线组成的连续多边形。其数学定义如下:假设P=p1, p2, p3, …, pn(3≤n < ∞)是二维欧氏空间(平面)上n个互不相同的点,则可以把点pi的Voronoi多边形V(pi)定义为
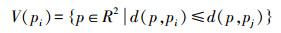 (1)
(1) 式中,i, j=1, 2, 3, …, n, i≠j,p为平面上的任意点;d(p, pi)与d(p, pj)分别为点p与pi和pj的欧氏距离;集合V={V(p1), V(p2), V(p3), …, V(pn)}所定义的图形即为以点集P为种子点生成的Voronoi图,如图 1所示。
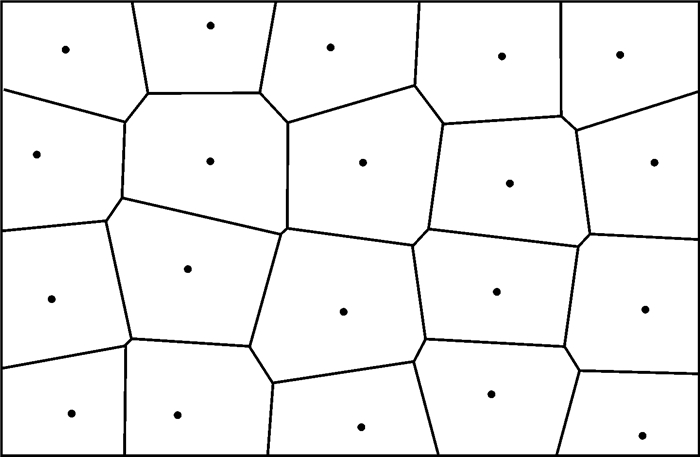
|
| 图 1 Voronoi图 |
原始影像基于DEM进行数字微分纠正后得到DOM影像,由于影像正射纠正时通常会发生旋转或DEM数据缺失,导致DOM影像出现无效值区域。
一般而言无效值区域分布于影像的四周,像素值被标记为0或255,可以采用边缘跟踪的方法获取影像有效多边形边界,此时的边界由连续像素点连接构成,节点数量过多,不利于后期进行多边形求交等操作。为了减少计算复杂度,可以使用Douglas-Peucker算法[12]进行点集抽稀。由于影像有效区域边界为闭合多边形,因此可以在点集中选定某一起点及距离其最远的一个节点,将多边形拆分为两条曲线段进行抽稀处理。图 2(a)和图 2(b)分别为单幅DOM边缘跟踪和点集抽稀结果。
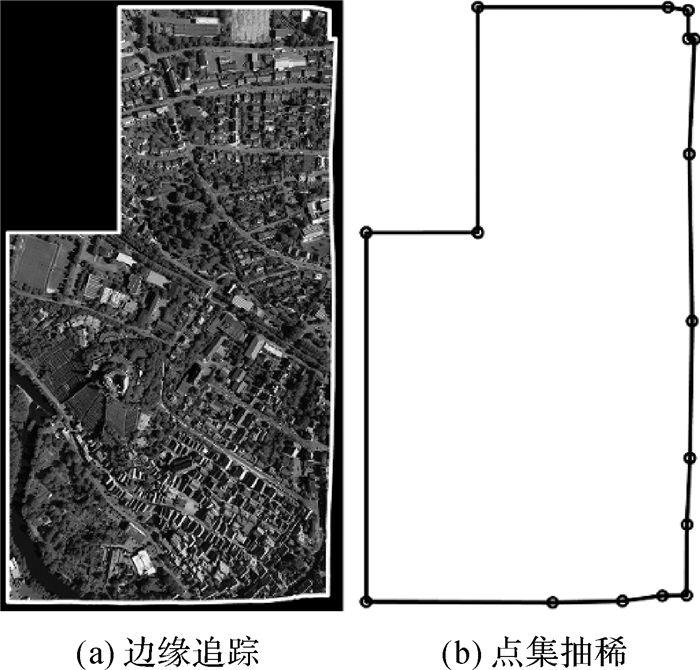
|
| 图 2 影像有效区域提取与点集抽稀 |
实际镶嵌处理时,首先获取每幅DOM影像的有效多边形范围,然后以多边形中心为种子点生成Voronoi图,对每幅影像进行划分,从而确定单幅影像在最终镶嵌结果影像上的有效区域,避免中间结果产生,以提高DOM生产效率与镶嵌的灵活性。
航空数码影像一般为中心投影成像方式,在投影中心区域几何畸变与投影差较小、图像质量较高、数字微分纠正后的DOM也是如此[13-14]。Voronoi图是基于散点最邻近原则的空间划分方法,因此生成初始镶嵌网络可以保留影像质量较高的区域,提高影像镶嵌和DOM生产精度。
2 镶嵌网络优化 2.1 顶点调整原则基于常规Voronoi图生成的镶嵌网络是根据影像中心点集对区域进行分割,没有考虑Voronoi多边形是否位于影像有效区域内,从而可能会在最终镶嵌影像上产生一些无数据的漏洞,尤其是当影像分布不均或影像间重叠区域不足时。因此需要对镶嵌多边形的顶点进行相应调整以避免镶嵌漏洞的产生。
Voronoi图中的每个顶点与三条边相连,并对应与其相关的3幅DOM影像。因此只需Voronoi网络中每一个顶点都位于与其相关的3幅影像有效多边形的重叠区域内,即可保证镶嵌线落在影像的有效重叠区域,从而避免无数据漏洞的出现。如图 3所示,当顶点位于V1处时,镶嵌影像的部分区域无有效数据覆盖(图中黑色区域),需将其调整至3张影像(P1, P2和P3)的重叠区域(图中灰色区域)内,即点V2,这样即可避免空洞区域的产生,实现正射影像无缝镶嵌。
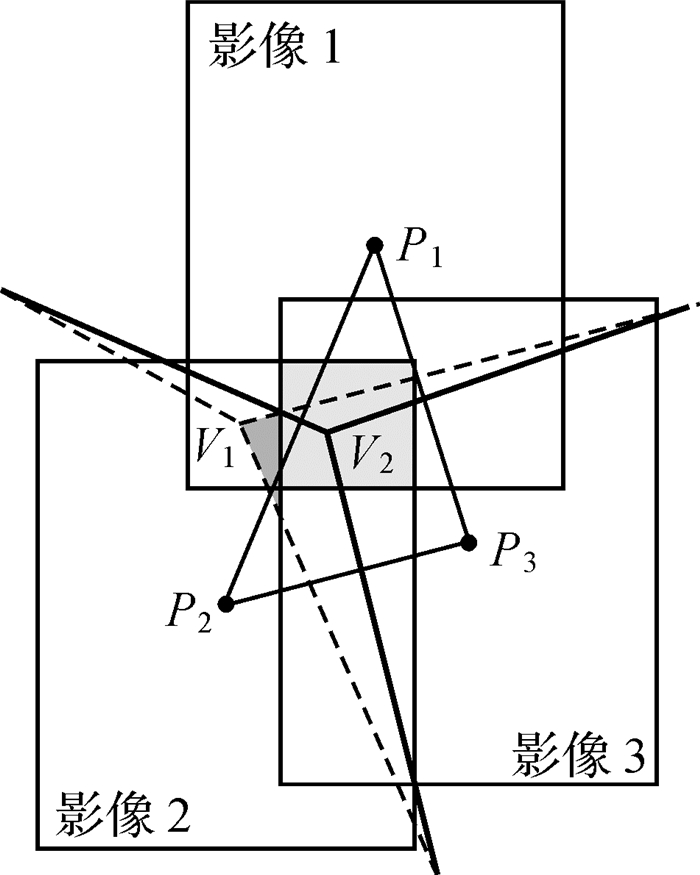
|
| 图 3 镶嵌效果示意图 |
对于以效率优先的影像拼接处理,一般只需实现无漏洞的拼接即可满足要求。而为了生产高质量、高精度的大范围DOM,需要使镶嵌线避开建筑、树木等存在投影差的地物区域。当镶嵌网络中的顶点位于这些地物上时,镶嵌线经过优化之后仍然会不可避免地穿越这些地物,产生几何错位与变形,因此顶点也应避开存在投影差的地物区域。由于DSM数据能够直接体现地物的高度信息与区域范围,并且一般与DOM产品一同生产,容易获取,因此本文结合DSM数据对镶嵌网络顶点位置进行进一步调整优化。
2.2 顶点调整方法对于多级别的DSM灰度影像,使用阈值分割将其分为障碍区域(建筑物、树木等)与非障碍区域(地面)。由于影像投影差的存在,顶点在DSM上紧贴障碍区域边缘时在原始DOM上可能表现为已穿越建筑物边缘部分。因此需要对DSM二值图像进行形态学膨胀[15]处理,填充建筑物与树木等障碍区域的空洞与凹陷,并使边缘往外扩展,最终使顶点偏离障碍区域,如图 4所示。

|
| 图 4 DSM处理结果 |
DSM处理完成后,基于处理影像对顶点进行调整,具体方法如下:以初始顶点v为圆心,从0开始以指定长度的步距不断增大半径r,在生成圆弧所经过的像素点集中,如果存在一点v′同时满足:①点v′在处理后DSM影像上的像素值为0;②点v′在3幅影像有效多边形重叠区域内,则以v′为新的顶点取代初始顶点v。
实际进行顶点调整时,为了保持镶嵌网络的拓扑性及多边形凹凸性,需要设置最大调整限制范围。如图 5所示,灰色区域为影像有效多边形重叠区域,记为VO;虚线区域为待调节顶点v相连接的3个Voronoi顶点构成的三角形,记为VT。则顶点调整的范围应限于VO与VT的交集多边形内,如图 5中阴影区域所示。
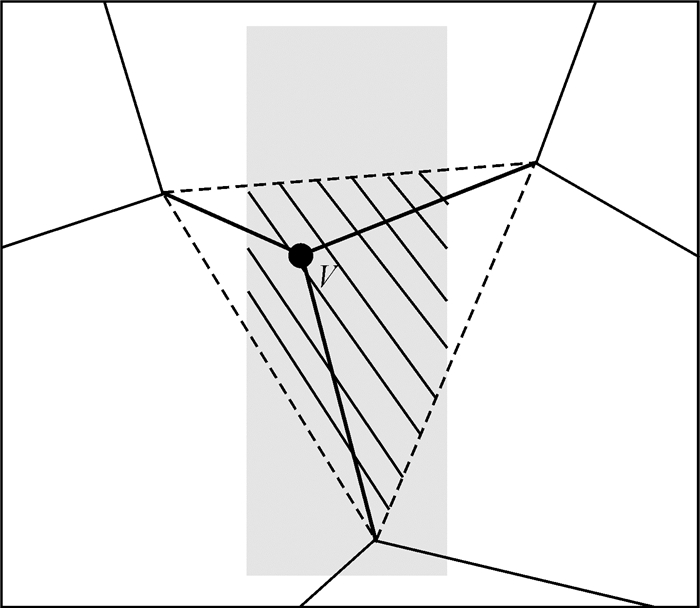
|
| 图 5 调整限制范围 |
顶点调整后可以使用已有学者提出的各类镶嵌线自动提取算法对初始镶嵌线进一步优化,使其避开建筑、树木和车辆等存在投影差的区域,避免产生几何错位与变形,形成高质量的无缝镶嵌影像。本文采用文献[2]提出的方法对镶嵌网络进行优化,对于每一段镶嵌线,在其最小外包矩形的基础上向外扩展一定范围,对所形成区域内的DSM数据进行处理生成搜索代价图,而后使用改进的JPS算法进行最优镶嵌线自动提取。
3 试验与结果分析 3.1 试验设计为了验证本文算法的可行性与有效性,基于C++(VC14)与OpenCV(3.2.0)实现了本文所提出的镶嵌网络生成方法。使用德国Vaihingen地区影像数据进行镶嵌网络生成试验,包括3个航带共14幅影像,航向与旁向重叠度均为60%;影像大小约为7680像素×13 824像素,空间分辨率为8 cm,正射纠正后重采样至0.2 m;影像对应的DSM分辨率为0.14 m。
3.2 结果分析试验中初始镶嵌网络生成与顶点调整结果如图 6所示,其中(b)、(c)和(d)分别为(a)中白色框内图像的局部放大显示。图 6(a)中黑色线条是以DOM影像有效区域中心点为种子点基于Voronoi图生成的初始镶嵌网络,由于仅考虑了影像中心点几何位置关系,生成的镶嵌网络中部分顶点位于房屋、树木等存在高投影差的区域,不利于接下来对镶嵌线进行走向优化。图 6(a)中白色线条为经过顶点调整后的镶嵌网络,可以看出,位于房屋处的顶点均被移至地面区域,而且Voronoi图的结构特性得以较好地保留。顶点调整后镶嵌网络中各条线段均位于影像有效重叠区域内,避免了拼接结果中影像数据丢失,形成无拼接漏洞的镶嵌影像。

|
| 图 6 初始镶嵌网络与顶点调整效果 |
顶点调整完成后,采用文献[2]提出的基于DSM与JPS算法的镶嵌线自动提取方法对初始镶嵌网络进行优化,从而使镶嵌线避开建筑和树木等存在投影差的地表区域。镶嵌网络优化结果如图 7所示,(b)、(c)和(d)分别为(a)中白色框内图像的局部放大显示。

|
| 图 7 镶嵌网络优化结果 |
本文提出了一种基于Voronoi图的正射影像镶嵌网络生成与优化方法,首先基于Voronoi图生成初始镶嵌网络;然后对镶嵌网络节点进行优化调整,确定每幅影像的有效多边形并保证无拼接漏洞产生;最后对每一段镶嵌线进行走向优化使其避开建筑、树木等区域,避免产生几何错位与色彩差异,形成最终的无缝镶嵌影像。本文方法与输入影像顺序无关,可以避免中间结果的产生,提高影像镶嵌的效率,能够满足大范围正射影像无缝拼接处理需求。值得注意的是,镶嵌网络顶点调整及镶嵌线走向优化效果主要取决于DSM的精度及阈值分割效果,后续将对DSM处理流程作进一步优化改进。
| [1] |
周清华, 潘俊, 李德仁. 遥感图像镶嵌接缝线自动生成方法综述[J]. 国土资源遥感, 2013, 25(2): 1-7. |
| [2] |
CHEN G, CHEN S, LI X, et al. Optimal seamline detection for orthoimage mosaicking based on DSM and improved JPS algorithm[J]. Remote Sensing, 2018, 10(6): 821-840. DOI:10.3390/rs10060821 |
| [3] |
KERSCHNER M. Seamline detection in colour orthoimage mosaicking by use of twin snakes[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2001, 56(1): 53-64. DOI:10.1016/S0924-2716(01)00033-8 |
| [4] |
ZHENG M, XIONG X, ZHU J. A novel orthoimage mosaic method using a weighted A* algorithm-implementation and evaluation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 138: 30-46. DOI:10.1016/j.isprsjprs.2018.02.007 |
| [5] |
陈继溢.正射影像镶嵌线快速检测方法研究[D].北京: 中国测绘科学研究院, 2015. http://cdmd.cnki.com.cn/Article/CDMD-86001-1015643510.htm
|
| [6] |
HE J, SUN M, CHEN Q, et al. An improved approach for generating globally consistent seamline networks for aerial image mosaicking[J]. International Journal of Remote Sensing, 2018, 40(3): 859-882. |
| [7] |
潘俊, 王密, 李德仁. 基于顾及重叠的面Voronoi图的接缝线网络生成方法[J]. 武汉大学学报(信息科学版), 2009, 34(5): 518-521. |
| [8] |
XANDRI R, PÉREZ F, PALÀ V, et al. Automatic generation of seamless mosaics over extensive areas from high resolution imagery[C]//World Multi-Conference on Systemics, Cybernetics and Informatics. Orlando: [s.n.], 2005.
|
| [9] |
HSU S, SAWHNEY H S, KUMAR R. Automated mosaics via topology inference[J]. IEEE Computer Graphics and Applications, 2002, 22(2): 44-54. DOI:10.1109/38.988746 |
| [10] |
潘俊, 王密, 李德仁. 接缝线网络的自动生成及优化方法[J]. 测绘学报, 2010, 39(3): 289-294. |
| [11] |
MILLS S, MCLEOD P. Global seamline networks for orthomosaic generation via local search[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 75: 101-111. DOI:10.1016/j.isprsjprs.2012.11.003 |
| [12] |
DOUGLAS D H, PEUCKER T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. The Canadian Cartographer, 1973, 10(2): 112-122. DOI:10.3138/FM57-6770-U75U-7727 |
| [13] |
张剑清, 孙明伟, 张祖勋. 基于蚁群算法的正射影像镶嵌线自动选择[J]. 武汉大学学报(信息科学版), 2009, 34(6): 675-678. |
| [14] |
袁修孝, 段梦梦, 曹金山. 正射影像镶嵌线自动搜索的视差图算法[J]. 测绘学报, 2015, 44(8): 877-883. |
| [15] |
龚声蓉. 数字图像处理与分析[M]. 北京: 清华大学出版社, 2014.
|



