大桥在人们生活中扮演着重要的角色,跨海大桥更是为人们的出行提供了方便。它处在海洋之上,不仅经受海水的冲击,还承受着车载的外力,发生形变后如果不进行充分的维护,就会影响桥体的使用,严重时会危及桥身的安全,引起坍塌,给社会和人类的生活带来极大的损失。因此,随时监测桥体的变形状态,并及时维护,不仅能保证桥身的正常运行,还能降低国家和人民的经济损失。由于桥梁的变形受很多因素的影响,使用传统的预测模型,难以精确判别桥梁变形程度。针对桥梁形变的非线性特点,需要使用非线性的预测模型进行分析。
非线性混沌时间预测是当今科学与工程技术领域研究的热点,但在变形分析方面的认识还不够深入,需要研究和解决的问题较很多[1]。因此,开展针对跨海大桥应用混沌理论进行时间序列预测的研究,深入了解并探寻大桥的变形规律,可为桥梁的维护和安全运行提供科学数据,对揭示跨海大桥变形机理、实现桥梁安全运营具有重大意义。本文对青岛胶州湾跨海大桥开展变形监测工作,在传统数据处理的基础上,进行非线性、动态的测量数据处理,并通过建立加权一阶局域预计模型和RBF神经网络混沌预计模型对其进行预测研究。
1 时间序列的相空间重构混沌系统形变轨迹经过长时间不断的变化,具有一定的规律可循。这种轨迹经过多种变化,变成一种与时间有关的序列时会呈现出混乱的特性。由于系统元素是相关的,因此所产生的数据点也是互相关联的。文献[2]提出使用原系统中的某个变量的延迟坐标进行相空间重构;文献[3]证实了可以找到合适的嵌入维数,即若延迟坐标的维数是动力系统的维数,在该嵌入维空间之中可以把这个有规则的轨迹还原出来,从而为混沌时间序列的预测理论打下基础。相空间重构的核心是延迟时间和嵌入维数的求取,传统的C-C算法和G-P算法能够准确求出重构参数[4-6],但这两种算法存在着不足之处。针对这些不足,本文使用改进的C-C算法和G-P算法,能够更好地完成相空间重构,可为后续预计模型的建立提供方便。
1.1 传统C-C算法原理C-C算法是应用关联积分构建时间序列的检验统计量来代表非线性时间序列的相关性,最终求取嵌入维数的计算方法。定义检验统计量,N为时间序列长度[7-8],即
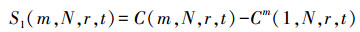 (1)
(1) 将时间序列分解为t个子序列,t为重构时延,当N→∞时,将统计量采用分块策略可表示为
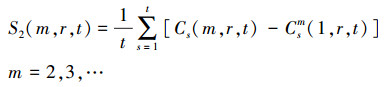 (2)
(2) 求取最大与最小两个半径r的差量如下
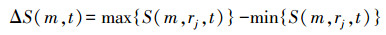 (3)
(3) 取m=2, 3, 4, 5, 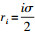
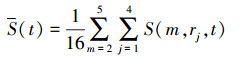 (4)
(4) 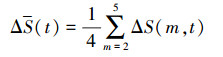 (5)
(5) 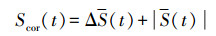 (6)
(6) 根据计算式(4)—式(6)寻找S(t)的第1个零点或ΔS(t)的第1个极小值,得到时间序列独立的第1个局部最大值,此时所求的t即为时间延迟。
1.2 C-C算法的改进传统C-C法存在4个问题:①关联积分中距离r的取值是一个定值,不能有效地体现出动态的混沌特性;②现实中S2(t)的第1个零点与ΔS2(t)的第1个极小点并不相等,且式(1)采用分块的方法,随着t的不断增大,ΔS2(t)会出现不断上升的高频起伏现象,当时间延迟τ较大时,这种现象尤为明显,会干扰ΔS2(t)的第1个极小值的选择;③定义关联积分时,只考虑m维向量中最大的一维,其他维数并没考虑,不符合实际情况;④计算效率较低。
针对以上4个问题,本文使用改进方案:①不在固定关联积分中进行距离r的取值,而是根据嵌入维数取相应的值;②S1(m, N, r, t)与S2(m, N, r, t)相比没有高频起伏现象,但有相同的规律,通过S1(m, N, r, t)求取S1(t)与ΔS1(t),并查找ΔS1(t)的第1个极小值点作为时间延迟;③将定义关联积分时使用的无穷范数改为F范数;④为了加快计算速度,将式(1)写成分块的方法计算关联积分,即
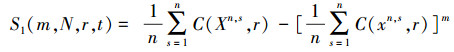 (7)
(7) 式中,Xn, s和xn, s分别为X和x的n个无重叠子集,n为常数,它可以控制计算精度和速度。当n=1时, S1(m, N, r, t)的计算精度最高;当n较大时,会存在一定的误差,但不同的时间之间只相差一个常数,因此不影响局部极值的读取。
1.3 传统G-P算法原理G-P算法从时间序列中计算吸引子的关联维数,对实测数据x(1),x(2),…, x(t)用Tankens嵌入维定理进行延时重构[9],得到一组空间向量X(t)=(x(t), x(t+τ), …, x[t+(m-1)τ]),t=1, 2,…, M,其中M=N-(m-1)τ, 对于空间中的M点,计算有关联向量的对数。间距小于指定正数r的向量都是关联向量,向量的距离一般有两种表示方法:2-笵数与∞-笵数,这里选用∞-笵数来计算,即将两向量最大分量作为距离。它在M2种可能中,配对所占的百分比称为关联积分
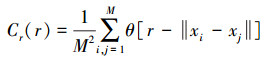 (8)
(8) 式中,θ(·)为Heaviside单位函数,即
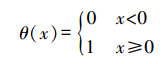 (9)
(9) 由此可计算关联积分Cr(r),选择不同邻域半径r,并分别对Cr(r)进行计算,然后拟合出Dm,增加m,最后得出饱和值D,根据m≥2D+1求出恰当的嵌入维数m[10]。
1.4 G-P算法的改进传统G-P算法存在4个问题:①寻找邻域半径r时,个人主观性很强,若r取值太小,则邻域内相位点太少,Cr(r)趋近于0,若r取值太大,则会包含所有的相位点,此时Cr(r)趋近于1,给嵌入维数的判别带来困难;②主要依赖人的观察来判别无标度区间,选取个人认为的线性区域,然后判别该区域线段的导数是否变化,这种主观占决定因素的判别容易产生误差;③邻域半径r变化步长的选择,步长太大,样本点数会变少,影响精度,步长太小,不仅增加运算量,同时也放大了噪声误差;④求取关联积分的方法在原理和结构上存在冗余,若不进行改善,不能满足实用性需要。
针对以上几个问题,本文采用以下方法进行改进:①邻域半径r的选择范围应该在相点间距的最小与最大的数值之间;②选定[ln(σ/3), ln(3σ)](σ为时间序列的标准差)为无标度区间的界限,找出Dm和m的函数关系,并画出关系曲线图,当曲线斜率趋近于0时,说明Dm趋于饱和;③步长从0开始线性递增,进行多次尝试;④在原始数据中读取相点的多维元素来计算相点间距离,不再进行多次重构,可以减轻大量的计算任务,当嵌入维数确定以后相点间距离不受r的影响,由于循环计算造成计算冗余,因此每进行一次相点距离的计算便与r进行一次比较,根据如下递推公式可以减少大量计算工作
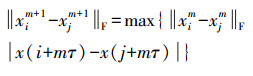 (10)
(10) 运用小数据量法求取最大Lvyapunov指数,小数据量法基本原理[11]为:根据重构的混沌时间序列的相空间,查询给定轨道上每个点的最小间距的邻点,即
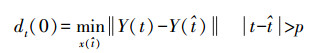 (11)
(11) 式中,
通过计算所有相邻最近两点的平均发散率的估算值获取最大Lyapunov指数,即
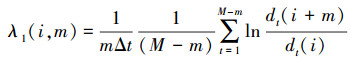 (12)
(12) 式中, m为常数;Δt为样本周期;dt(i)为第t组相邻最近的两点经过i个离散时间的步长距离。对dt(i)取对数得
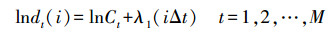 (13)
(13) 最大Lyapunov指数可通过近似于式(13)中直线的斜率获得。
3 混沌时间序列预测 3.1 加权一阶局域预测模型在相空间之间计算每个邻域点到X(t)之间的欧氏距离,并找出X(t)的参考向量集X(ti), i=1, 2, …, N,且点X(ti)与X(t)的区间为d,假设dm为di中的最小量,定义点权值为[12]
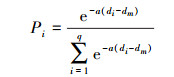 (14)
(14) 式中,a为常系数,通常取a=1。则一阶局域线性拟合为
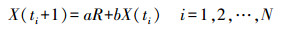 (15)
(15) 式中,R=[1 1···1]T。嵌入维数m=1时,采用加权最小二乘法,有
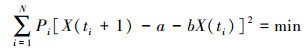 (16)
(16) 对式(16)中与a、b有关的函数求偏导,并求解a和b,代入可以求取预测值如下
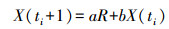 (17)
(17) 径向基函数RBF神经网络将前馈网络分为3层:第1层为输入层,由信号源节点组成[13];第2层为隐含层,将输入空间投影到新的空间,根据问题的需要确定单元数;第3层为输出层,对输入模式的作用作出反应[14]。
RBF网络进行投影f:Rn→Rm,其数学表达式为
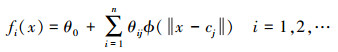 (18)
(18) 式中m=1;x∈Rn为网络的输入变量;径向基函数为ϕ(·),非线性变换为Rn→R;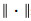
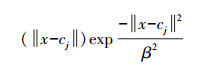 (19)
(19) 式中,β表示宽度值,为常数。
RBF神经网络混沌预测的步骤为[15]:
(1) 对时间序列进行归一化处理,所得数据分为预测部分和训练部分;利用时间延迟和嵌入维数m两个重构参数对训练部分进行相空间重构,重构后的点数为N=n-(m-1)。
(2) 通过调用newrb函数建立径向基神经网络的预测模型,其格式为net=newrb(P, T, goal, SPERAD, MN, DF),其中,P为输入向量,m个输入层元素;T为目标向量;SPREAD为隐含层的分布密度;指定元素的最大数目为MN;DF为两次显示时间间隔内所增加的神经元数量。newrb函数内部确定线性变换及非线性变换、初始偏离值与初始值。用RBF网络逼近函数时,newrb可以自动添加网络中的隐层神经元,当均方误差满足限差时停止,此时所用的网络输出为an=sim(net, P)。
(3) 取中心向量X(N)=(x(n-(m-1)τ), x(n-(m-2)τ), …, x(n))作为输入RBF神经网络,进行预测得到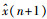
预测过程中存在多种不确定因素,若预测结果不科学,建立的模型就不能用在桥梁变形数据处理中,因此需要采用科学的评价标准进行评定。评定的方法有很多种,本文采用以下两种方法:
(1) 平均绝对误差(MAE):计算每期实际值与预测值绝对误差的平均值,公式如下
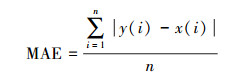 (20)
(20) (2) 均方根误差(RMSE):求取绝对误差平方和的平均值,然后将平均值进行开方,计算公式如下
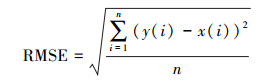 (21)
(21) 式中,y(i)为第i点的预测值;x(i)为第i点的实测值;n为期数。
4 应用实例本次观测高程基准网共布设7个控制点,其中3个已知的基准点。根据《国家一、二等水准测量规范》(GB/T 12897—2006)规定的二等水准测量要求对青岛胶州湾大桥的高程基准网进行观测。采用精度为0.6 mm的Trimble DINI03数字水准仪及配套铟瓦条码尺,按“后前前后”奇偶交替模式对青岛胶州湾大桥进行往返观测,数据合格后取其平均值作为项目实测数据,确保变形数据的可靠性。从2017年4月—2017年10月期间连续检测的数据中每3 d取一期形成等间隔的时间序列,共70期数据。下沉值计算均以第1期观测数据为基准。以沉降点R6为例,下沉数据如图 1所示。
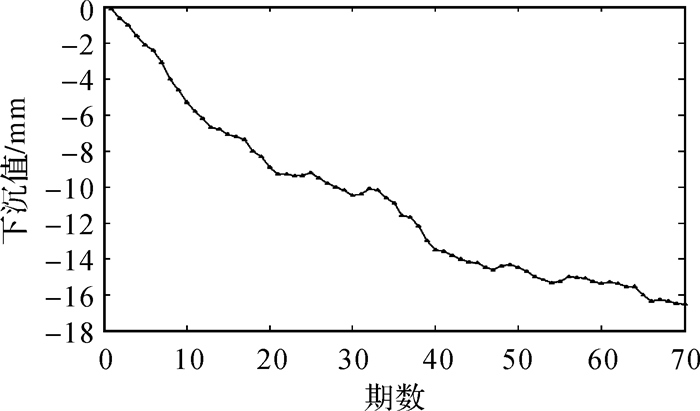
|
| 图 1 观测数据 |
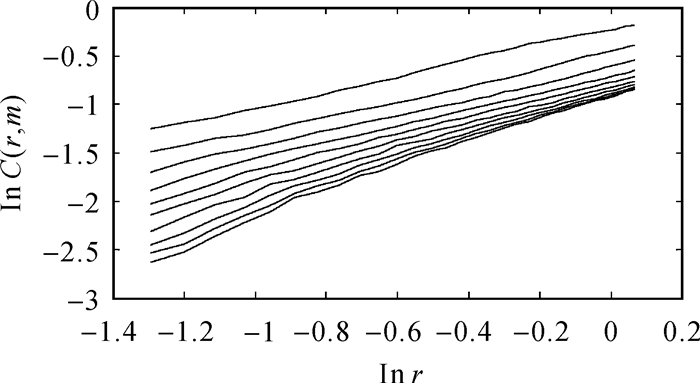
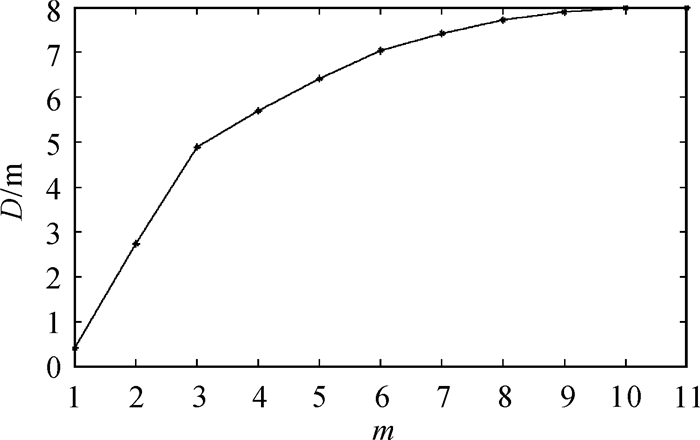
图 2、图 3中的ΔS(t)和Scor(t)都在τ=7时达到第1个近似极小点,因此时间序列的时间延迟τ=7。由图 2、图 3可以看出,改进的C-C方法与传统方法相比,第1个近似极小点明显易读,不存在干扰现象。由图 4、图 5可以看出,维数增加到10时曲线斜率不再变化,图 5与图 4相比易于观察,减少了主观因素,证明了无标度区间选取的合理性。由图 6可知,当嵌入维数m=10时,D趋向于饱和,因此嵌入维数为10。改进的G-P算法与传统算法相比计算速度快,计算出的关联维数接近理论值,说明该方法可行性较强。
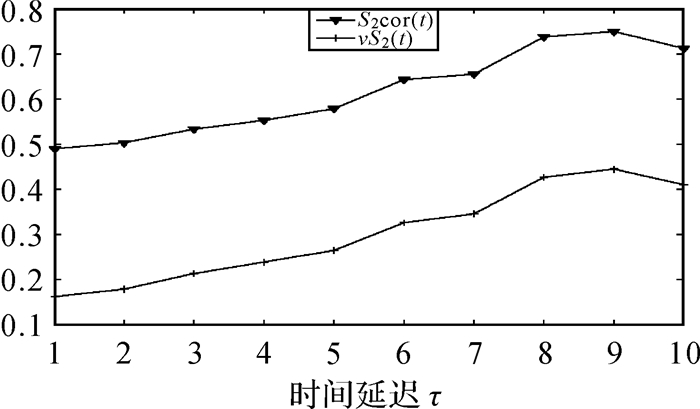
|
| 图 2 传统C-C法求时间延迟 |
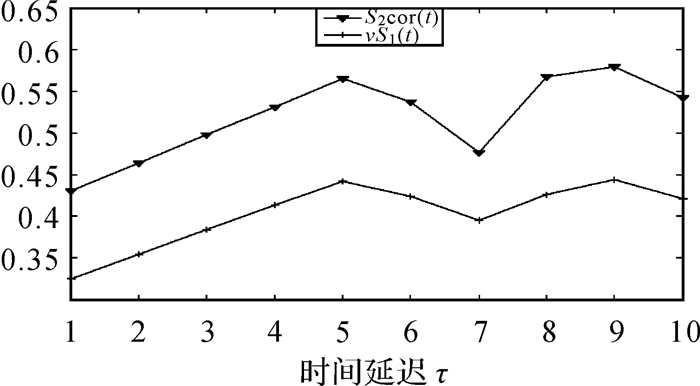
|
| 图 3 改进C-C法求时间延迟 |
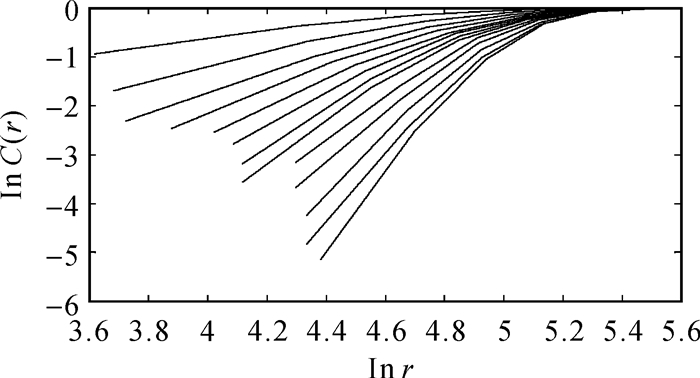
|
| 图 4 传统G-P法求取嵌入维数 |
|
| 图 5 改进G-P法求取嵌入维数 |
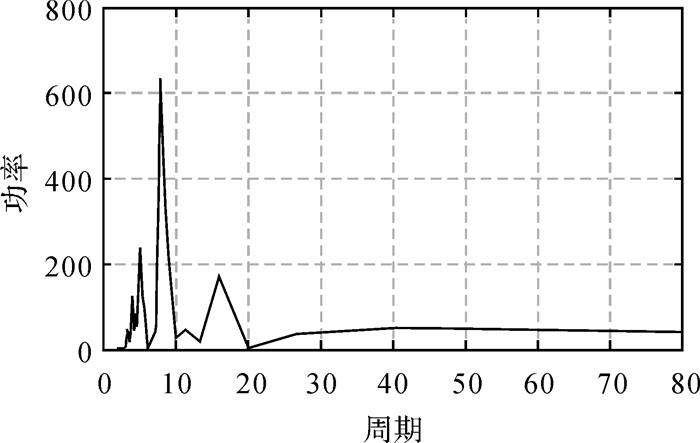
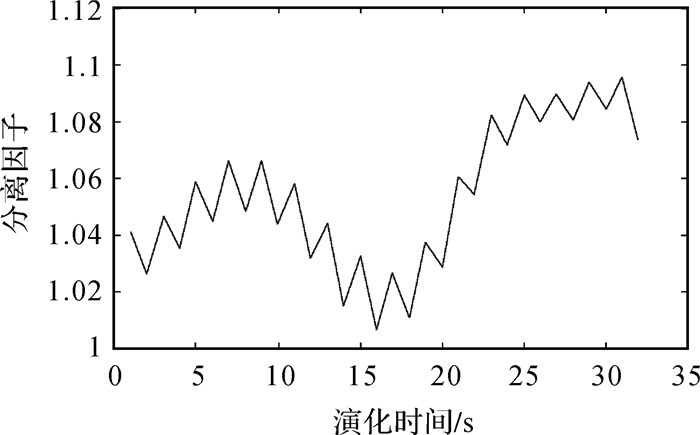
通过小数量法对桥墩沉降时间序列进行混沌性判别。使用FFT估计时间序列的平均周期,根据重构参数τ和m,求取时间序列的最大Lyapunov指数λ。周期—功率图和最大Lyapunov指数计算图如图 7、图 8所示。时间序列周期P=8,最大Lyapunov指数为0.034 5,大于0,可以确定此时间序列存在混沌迹象[16];同时,系统最长预报时间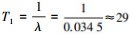
|
| 图 6 关联积分D(m)-m关系 |
|
| 图 7 周期—功率谱 |
|
| 图 8 最大Lyapunov指数计算 |
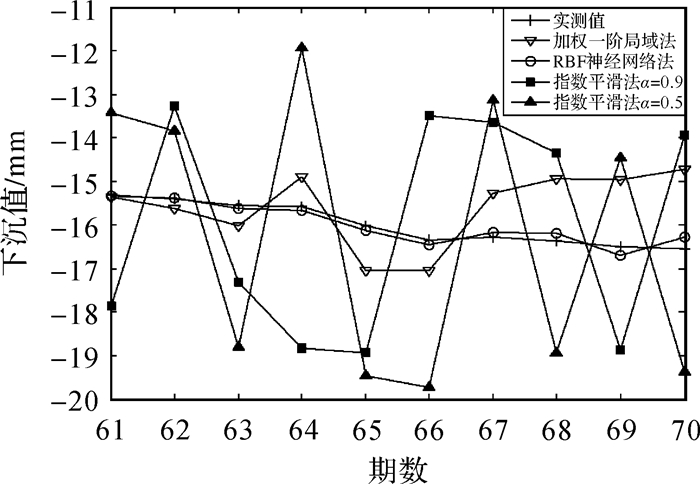
本文运用两种混沌时间序列预测方法对跨海大桥沉降数据进行预计:①根据时间延迟τ=0和嵌入维数m=10对时间序列进行相空间重构,建立加权一阶局域预测模型[17];②对时间序列进行归一化,取前60期数据作为训练样本,再根据前面所求的时间延迟和嵌入维数进行相空间重构,建立RBF神经网络混沌预测模型[18];③使用以上两种混沌预计模型及系数为0.9和0.5的指数平滑法对时间序列进行短期预测。系统最长预报时间为87 d,为保证预测精度,预测数据选取后30 d观测的最后10期数据对比分析预测结果。如表 1和图 9所示。
| 预测期数 | 实测值/mm | 加权一阶局域预测 | RBF神经网络混沌预测 | 指数平滑法预测 | |||||||||||||
| 预测值/mm | 绝对误差/mm | 相对误差/(%) | 预测值/mm | 绝对误差/mm | 相对误差/(%) | 预测值/mm | 绝对误差/mm | 相对误差/(%) | |||||||||
| α=0.9 | α=0.5 | α=0.9 | α=0.5 | α=0.9 | α=0.5 | ||||||||||||
| 61 | -15.32 | -15.36 | -0.04 | 0.26 | -15.34 | -0.02 | 0.13 | -17.85 | -13.43 | -2.53 | 1.89 | 16.51 | 12.34 | ||||
| 62 | -15.41 | -15.61 | -0.20 | 1.30 | -15.37 | 0.04 | 0.26 | -13.28 | -13.85 | 2.13 | 1.56 | 13.82 | 10.12 | ||||
| 63 | -15.56 | -16.01 | -0.45 | 2.89 | -15.62 | -0.06 | 0.39 | -17.31 | -18.81 | -1.75 | -3.25 | 11.25 | 20.89 | ||||
| 64 | -15.57 | -14.89 | 0.68 | 4.37 | -15.66 | -0.09 | 0.58 | -18.82 | -11.94 | -3.25 | 3.63 | 20.87 | 23.31 | ||||
| 65 | -16.02 | -17.04 | -1.02 | 6.37 | -16.13 | -0.11 | 0.69 | -18.94 | -19.47 | -2.92 | -3.45 | 18.23 | 21.54 | ||||
| 66 | -16.35 | -17.05 | -0.70 | 4.28 | -16.45 | -0.1 | 0.61 | -13.49 | -19.72 | 2.86 | -3.37 | 17.49 | 20.61 | ||||
| 67 | -16.29 | -15.27 | 1.02 | 6.26 | -16.16 | 0.13 | 0.80 | -13.64 | -13.13 | 2.65 | 3.16 | 16.27 | 19.40 | ||||
| 68 | -16.36 | -14.95 | 1.41 | 8.62 | -16.20 | 0.16 | 0.98 | -14.34 | -18.93 | 2.02 | -2.57 | 12.35 | 15.71 | ||||
| 69 | -16.49 | -14.97 | 1.52 | 9.22 | -16.70 | -0.21 | 1.27 | -18.88 | -14.46 | -2.39 | 2.03 | 14.49 | 12.31 | ||||
| 70 | -16.55 | -14.73 | 1.82 | 11.00 | -16.29 | 0.26 | 1.57 | -13.92 | -19.38 | 2.63 | -2.83 | 15.89 | 17.10 | ||||
|
| 图 9 两种方法预测对比 |
由表 1可以看出,混沌时间序列预测结果比指数平滑预测结果更接近实测值,说明混沌时间序列预测方法的可靠性;RBF神经网络混沌时间序列预计效果优于加权一阶局域法预计效果。由图 9可知,两种模型预测结果都与真实值相差不大,且随着期数的增加,两种模型预计值与实测值的差距越来越大,预测误差随着预测时间的增加呈递增趋势,但最大相对误差为11%,说明混沌预测法在桥梁变形监测中进行短期预测是可行的。
对以上3种模型的预测精度进行评定,结果见表 2。
| 预测模型 | 加权一阶局域预测模型 | RBF神经网络混沌预测模型 | 指数平滑法预测模型 | |
| α=0.9 | α=0.5 | |||
| 均方根误差 | 1.043 | 0.138 | 2.550 | 2.859 |
| 平均绝对误差 | 0.886 | 0.118 | 2.513 | 2.774 |
从表 2中定量数值可看出,加权一阶局域法和RBF神经网络混沌法预测精度明显高于指数平滑法,RBF神经网络混沌法计算精度优于加权一阶局域法,表明混沌时间序列预测方法可靠,能够反映桥梁变形的真实状态。
5 结论本文根据青岛胶州湾跨海大桥的变形监测数据,提出了桥梁变形混沌状态判别标准,给出了桥梁变形混沌相空间重构方法;并综合神经网络非线性数据处理的能力,建立了桥梁变形神经网络混沌时间序列预计模型。结论如下:
(1) 采用改进的C-C法计算时间序列的时间延迟τ,采用改进的G-P法计算最佳嵌入维数m,通过这两个重构参数,对桥梁实测数据进行了相空间重构,实例表明与传统算法相比,改进算法的抗干扰性、计算效率等方面都得到了改善。
(2) 建立了混沌预测模型,将混沌预测方法预测精度与指数平滑法预测精度进行比较,前者预测精度明显高于后者,RBF神经网络混沌法预测精度优于加权一阶局域法。
| [1] |
XIONG L, LIU Z L, ZHANG X G. Dynamical analysis, synchronization, circuit design, and secure communication of a novel hyperchaotic system[J]. Complexity, 2017, 20(3): 1-23. |
| [2] |
陈演羽, 李廷会, 黄飞江, 等. 基于混沌时间序列的GPS卫星钟差预测算法[J]. 仪器仪表学报, 2018, 33(4): 115-122. |
| [3] |
秦四清, 张倬元, 王士天, 等. 非线性工程地质学导引[M]. 成都: 西南文通大学出版社, 1993: 16-20.
|
| [4] |
王新迎, 韩敏. 多元混沌时间序列的多核极端学习机建模预测[J]. 物理学报, 2015, 64(7): 37-143. |
| [5] |
栾元重, 栾亨宣, 马德鹏, 等. 桥梁变形数据小波去噪与混沌预测[J]. 大地测量与地球动力学, 2013, 33(5): 133-135, 139. |
| [6] |
王建波, 栾元重, 许君一, 等. 小波分析桥梁变形监测数据处理[J]. 测绘科学, 2012, 37(3): 79-81. |
| [7] |
卢天秀.关于几类系统混沌性的研究[D].成都: 电子科技大学, 2013: 1-7. http://cdmd.cnki.com.cn/Article/CDMD-10614-1014137372.htm
|
| [8] |
SU L Y, SUN H H, WANG J, et al. Detection and estimation of weak pulse signal in chaotic background noise[J]. Acta Physica Sinica, 2017, 66(9): 23-36. |
| [9] |
吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2005: 57-85.
|
| [10] |
GRASSBERGER P, PROCACCIA I. Measuring the strangeness of strange attractors[M]. New York: Springer, 2004: 189-208.
|
| [11] |
李海波.混沌时间序列预测应用研究[D].合肥: 中国科学技术大学, 2009: 19-25. http://cdmd.cnki.com.cn/article/cdmd-10358-2010019378.htm
|
| [12] |
刘利强.基于IABC-RBF算法和小波分析的瓦斯时间序列优化预测[D].辽宁: 工程技术大学, 2015: 33-39. http://cdmd.cnki.com.cn/Article/CDMD-10147-1016059400.htm
|
| [13] |
ZHANG R D, TAO J L, LU R Q, et al. Decoupled ARX and RBF neural network modeling using PCA and GA optimization for nonlinear distributed parameter systems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(2): 457-469. DOI:10.1109/TNNLS.2016.2631481 |
| [14] |
雷宇.基于RBF神经网络的电梯故障诊断方法研究[D].武汉: 武汉理工大学, 2015: 12-20. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D01038525
|
| [15] |
李文华, 马思宁, 沈培根, 等. 振动条件下铁路继电器寿命预测研究[J]. 电气工程学报, 2017, 12(7): 8-15. |
| [16] |
徐国宾, 赵丽娜. 基于多元时间序列的河流混沌特性研究[J]. 泥沙研究, 2017, 42(3): 7-13. |
| [17] |
王超, 朱明, 赵元棣. 基于改进加权一阶局域法的空中交通流量预测模型[J]. 西安交通大学学报, 2018, 53(1): 206-213. |
| [18] |
莫小琴, 李钟慎. 混沌时间序列的LSSVM预测方法[J]. 华侨大学学报(自然科学版), 2014, 35(4): 373-377. |


