2. 甘肃省地理国情监测工程实验室, 甘肃 兰州 730070
2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China
可降水量(precipitable water vapor,PWV)对中小尺度灾害性天气预报具有指示意义,是降雨强度预报的重要参数之一。自20世纪80、90年代起,国外已经对GPS探测大气可降水量进行了大量研究[1-2]。国内最早由毛节泰引进并详细介绍了地基GPS反演大气可降水量的方法[3],近年来发展迅速并取得了一定的成果[4-10]。随着中国北斗卫星导航系统(BeiDou navigation satellite system,BDS)提供服务并不断地建设完善,其已经能够应用到气象学领域,可以获得大气可降水量。文献[11]利用河北省6个测站的数据分别估算GPS、BDS天顶总延迟量(zenith total delay,ZTD),两者之间的标准差为5~6mm。文献[12]利用亚太地区10个测站BDS数据采用精密单点定位方法进行大气可降水量反演,反演结果与GPS结果相比均方根误差为2mm左右。文献[13]采用精密单点定位方法,分别采用3种方案(BDS、GPS和BDS+GPS)来估算PWV,BDS精密单点定位可作为新的数据源,可独立提供高精度的ZTD与PWV产品且精度较高,同时BDS+GPS组合系统反演得到的可降水量精度更高。文献[14]利用上海市气象局建立的北斗气象站的观测数据及PANDA软件实现了基于北斗数据的大气可降水量反演,与探空数据计算结果及GPS数据反演结果之间的均方根误差约为3.5mm,相关系数均在0.95以上。
此外,GAMIT软件自10.5版本开始,就逐步加入对其他全球卫星导航系统(global navigation satellite system,GNSS)的支持。随着10.61版本的发布,软件已经可以支持北斗观测数据的解算,并且附带的共用表文件也包含了多个GNSS系统的信息。截至目前,GAMIT软件已更新到10.70版本。因此,本文首次利用GAMIT软件对利用北斗系统数据反演大气可降水量进行研究,并结合探空数据计算得到的PWV与GPS反演得到的PWV进行精度验证,以期增强北斗卫星导航系统在大气水汽监测中的研究和应用。
1 大气可降水量计算方法 1.1 无线电探空资料大气可降水量计算方法基于探空气球的大气可降水量是利用探空气球观测气象对流层中各高度上的比湿q(单位g/kg),然后对大气压力p(单位hPa)从地面到对流层上界进行垂直积分而得,即
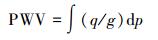 (1)
(1) 式中,PWV为可降水量,单位为mm;g为地球重力加速度。实际计算时,可以用各个标准等压面上的比湿值进行差分计算以代替积分,而且由于大气水汽几乎全部集中在气象学定义的对流层(0~12km),计算时采用分层叠加的办法进行。计算步骤如下:
(1) 根据各高度上的露点温度测值,算出各高度上的水汽压e(单位hPa),计算式为
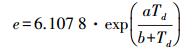 (2)
(2) 式中,Td为露点温度, 单位为℃。系数a、b的取值为:气温低于-40℃时,a=21.87,b=265.49;气温高于0℃时,a=17.26,b=237.29;若气温居于两者之间,a、b用线性内插算出。
(2) 根据各高度上的气压测值和式(2)算出的水汽压,可计算比湿q,即
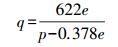 (3)
(3) (3) 计算大气可降水量PWV,计算式为
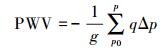 (4)
(4) 式中,p0为地面大气压力,单位为hPa。
1.2 地基GNSS反演可降水量基于地基GNSS的大气可降水量反演步骤为:①由高精度GNSS数据处理软件——GAMIT软件根据原始观测数据解算出各测站天顶总延迟量;②根据气象观测资料与天顶静力延迟模型计算出天顶静力学延迟量(zenith hydrostatic delay,ZHD);③用天顶总延迟量减去天顶静力延迟量获得天顶湿延迟量(zenith wet delay,ZWD),即ZWD=ZTD-ZHD;④结合下式,根据加权平均温度模型确定水汽转换系数Π,将天顶湿延迟转换为可降水量PWV。
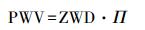 (5)
(5) 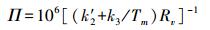 (6)
(6) 式中,Rv=461.495J/(kg·K), 为气体常数;k′2=22.13、k3=3.793×105,均为大气折射常数;Tm为加权平均温度,单位为K。
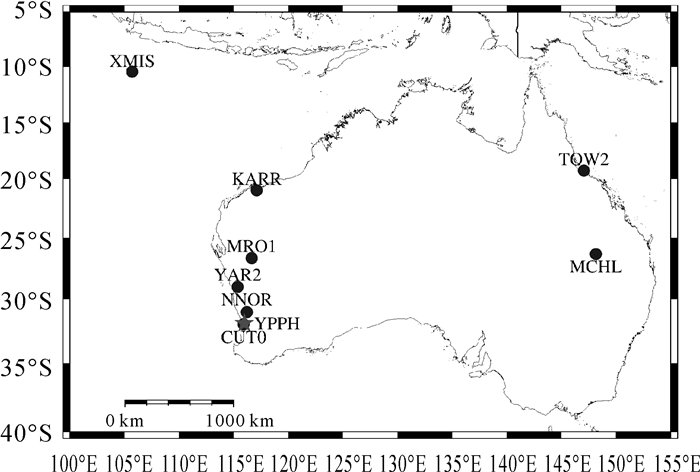
2 数据来源与处理方法 2.1 数据来源基于近年发展起来的多模GNSS试验跟踪网(multi-GNSS experiment,MGEX)数据,选取澳大利亚地区的8个MGEX站2018年1月1日至2018年1月15日的原始观测数据,均包括GPS、BDS、Galileo与GLONASS等数据,站点分布如图 1所示。图中,YPPH为探空站,站点编号为94610,与CUT0站相距不到10km。
|
| 图 1 站点分布 |
利用Matlab软件编写代码读取探空数据并计算相应的大气可降水量值,数据采样间隔为12h(分别为UTC 0时、12时)。采用GAMIT 10.70软件分别进行基于GPS、BDS数据的大气可降水量反演,GAMIT 10.70软件已经能够处理RINEX 3格式的文件输入,即在不进行格式转换的情况下,可以直接对RINEX 3的观测数据与卫星星历进行处理。但其不足之处在于目前暂不支持RINEX 3格式的文件名,因此在解算之前,应通过GAMIT自带的脚本sh_rename_rinex3将RINEX 3格式的文件重命名为RINEX 2格式的文件。GAMIT解算时主要采用的解算策略为:①卫星截止高度角设置为15°;②历元间隔为30s;③采用消除电离层后的组合观测值;④解算模式采用周跳自动修复技术;⑤采用CODE的电离层产品;⑥轨道解类型采用松弛解;⑦考虑大气负荷和海潮负荷,海潮模型采用otl_FES2004.grid;⑧采用“全球气压和温度”模型值作为某一测站的先验气压和温度;⑨加权平均温度模型采用Bevis经验公式;⑩对流层折射模型采用Saastamoinen模型估算天顶延迟参数,投影函数采用VMF1模型,引入全球大气映射函数模型文件map.grid,采用分段线性的方法估算折射量偏差参数,每两小时估计一个参数。
3 结果分析 3.1 基线解算结果评判GAMIT基线解算结果的精度指标较多,本文主要以标准化均方根误差(normalized root mean square,NRMS)和基线重复性作为判断标准。从年积日目录下Q文件中提取NRMS值,经统计发现,GPS数据基线解算后所对应的NRMS值均小于0.2,其平均值为0.1688;而BDS数据基线解算后所对应的NRMS值也均小于0.2,平均值为0.1763,略大于GPS数据所对应的NRMS平均值。统计基线重复性结果可得出,GPS数据、BDS数据所对应的基线解算的精度都在10-8量级以上,GPS基线重复性结果精度略高于BDS,均满足地壳形变要求的10-7量级。因此,较高的基线解算结果精度为大气可降水量反演的精度奠定了基础。
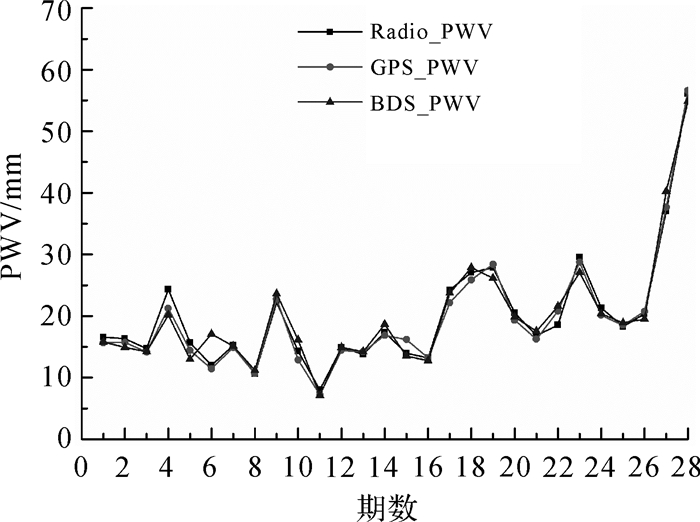
3.2 与探空数据计算结果的对比无线电探空仪是气象部门常用的大气数据探测方法,精度较高,常用作新方法的检验标准。CUT0站与探空站YPPH相距几千米,因此对两者进行对比。此外,由于探空站YPPH采样间隔为12h,而且在2018年1月10日UTC 12时、2018年1月15日UTC 12时没有观测数据,因此总共有28期结果可进行对比分析。对比结果如图 2、表 1所示。其中,探空资料计算得到的大气可降水量结果用Radio_PWV表示;通过GPS与BDS数据反演得到的大气可降水量分别用GPS_PWV与BDS_PWV表示。
|
| 图 2 反演结果与探空数据计算结果对比 |
| PWV精度对比情况 | 样本数 | 平均绝对误差/mm | 均方根误差/mm | 相关系数 |
| Radio_PWV与GPS_PWV | 28 | 0.9014 | 1.1526 | 0.9932 |
| Radio_PWV与BDS_PWV | 28 | 1.3929 | 1.8570 | 0.9800 |
从图 2和表 1可以看出,基于GPS、BDS反演得到的大气可降水量与无线电探空数据计算得到的大气可降水量变化趋势基本保持一致,经统计发现,反演结果相对应的平均绝对误差与均方根误差均小于2mm,相关系数均大于0.98。不难看出,BDS反演结果精度较GPS反演结果精度差一点,但是能满足气象观测需要,符合目前国际上要求的3~4mm的精度[15]。
3.3 与GPS反演结果对比由于篇幅有限,仅对CUT0、KARR、MCHL、MRO1这4站反演结果进行对比,分别绘制反演结果比较图,如图 3所示。可以看出,在4站中,GPS、BDS反演结果趋势基本一致。经统计分析,其精度对比见表 2。在4站中,BDS_PWV与GPS_PWV之间的平均绝对误差均小于3mm,最大为2.0458mm;在均方根误差方面,BDS_PWV与GPS_PWV之间的均方根误差均小于3mm,最大值为2.6915mm。在相关系数方面,明显可以看出,相关系数均大于0.96,基本满足气象观测需要,也符合目前国际上要求的3~4mm的精度。

|
| 图 3 GPS与BDS反演结果对比 |
| 站点 | 样本数 | 平均绝对误差/mm | 均方根误差/mm | 相关系数 |
| CUT0 | 195 | 1.3117 | 1.8237 | 0.9901 |
| KARR | 195 | 2.0458 | 2.6915 | 0.9658 |
| MCHL | 195 | 2.0235 | 2.6811 | 0.9643 |
| MRO1 | 195 | 1.6210 | 2.1354 | 0.9877 |
本文通过选取MGEX数据网站提供的2018年1月1日至2018年1月15日15天的混合星历的原始观测数据,包括RINEX格式的观测值文件与气象数据文件、精密星历文件及广播星历文件,进行了基于GAMIT软件的BDS大气可降水量反演研究,并与探空数据计算得到的大气可降水量及GPS反演得到的大气可降水量进行了对比,得出以下结论:
(1) BDS数据基线解算的NRMS值均小于0.2,精度在10-8量级,略低于GPS数据基线解算结果,总体而言基线解算结果精度较高,为大气可降水量反演精度奠定了基础。
(2) 通过GPS、BDS反演得到的可降水量与探空数据计算结果之间的均方根误差小于2mm,相关系数均大于0.98,GPS反演结果精度与探空数据计算结果更接近,均符合目前国际上要求的3~4mm的精度。
(3) BDS数据反演得到的大气可降水量与GPS反演结果之间的均方根误差小于3mm,相关系数均大于0.96,均能满足气象观测需要。
(4) 由于区域的差异性,本文所采用Bevis经验公式进行研究区域的大气可降水量反演时,可能产生局域模型系统误差。此外,对流层折射模型与映射函数等均会使反演得到的大气可降水量产生误差,因此得到的大气可降水量值并非最优值。
| [1] |
BEVIS M, BUSINGER S, HERRING T A, et al. GPS meteorology:remote sensing of atmospheric water vapor using the global positioning system[J]. Journal of Geophysical Research Atrnospheres, 1992, 97(D14): 15787-15801. DOI:10.1029/92JD01517 |
| [2] |
DUAN J, BEVIS M, FANG P, et al. GPS meteorology:direct estimation of the absolute value of precipitable water[J]. Journal of Applied Meteorology, 1996, 35(6): 830-838. DOI:10.1175/1520-0450(1996)035<0830:GMDEOT>2.0.CO;2 |
| [3] |
毛节泰. GPS的气象应用[J]. 气象科技, 1993, 21(4): 45-49. |
| [4] |
姚宜斌, 张顺, 孔建. GNSS空间环境学研究进展和展望[J]. 测绘学报, 2017, 46(10): 1408-1420. DOI:10.11947/j.AGCS.2017.20170333 |
| [5] |
徐韶光, 熊永良, 刘宁, 等. 利用地基GPS获取实时可降水量[J]. 武汉大学学报(信息科学版), 2011, 36(4): 407-411. |
| [6] |
郑加柱, 王亮. 江苏地区大气可降水量的时空分布[J]. 东南大学学报(自然科学版), 2013, 43(S2): 260-264. |
| [7] |
李森, 贾光军. GNSS技术下北京7·21暴雨水汽含量反演分析[J]. 测绘通报, 2018(6): 78-81. |
| [8] |
姚宜斌, 曹娜, 许超钤, 等. GPT2模型的精度检验与分析[J]. 测绘学报, 2015, 44(7): 726-733. |
| [9] |
毛鹏宇, 陈义, 孟鑫. 气象数据缺失时地基GPS反演可降水量方法研究[J]. 大地测量与地球动力学, 2017, 37(10): 1049-1052. |
| [10] |
陈于, 赵遐龄, 王开通, 等. GPS天顶对流层延迟与可降水量的相关性[J]. 测绘科学, 2016, 41(8): 59-62. |
| [11] |
XU A, XU Z, GE M, et al. Estimating zenith tropospheric delays from BeiDou navigation satellite system observations[J]. Sensor, 2013, 13(4): 4514-4526. DOI:10.3390/s130404514 |
| [12] |
LI M, LI W, SHI C, et al. Assessment of precipitable water vapor derived from ground-based BeiDou observation with precise point positioning approach[J]. Advances in Space Research, 2015, 55(1): 150-162. |
| [13] |
韩阳, 吕志伟, 徐剑, 等. 基于BDS/GPS观测量的大气可降水量反演精度分析[J]. 导航定位学报, 2017, 5(1): 39-45. |
| [14] |
郭巍, 尹球, 杜明斌, 等. 利用地基北斗站反演大气水汽总量的精度检验[J]. 应用气象学报, 2015, 26(3): 346-352. |
| [15] |
曹玉静.应用地基GPS技术反演加拿大新布伦瑞克地区大气可降水量[C]//《测绘通报》测绘科学前沿技术论坛摘要集.北京: 测绘出版社, 2008: 1-5.
|



