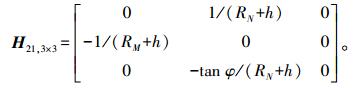2. 清华大学导航技术工程中心, 北京 100089
2. Engineering Research Center for Navigation Technology, Tsinghua University, Beijing 100089, China
天文导航(CNS)是一种利用光学探测设备测得恒星、近天体的信息来解算获得载体精确姿态的自主导航技术,具有测量精度高、无误差累积等优点,已成为船载高精度姿态测量的一种主要手段[1]。但是其容易受天气环境的影响,在多云或缺星环境下通常无法独立完成导航定姿的任务。因此, 将GNSS+INS组合导航系统与CNS结合起来,可提供无缝的高精度定位定姿结果,并有效保障天文导航在具备可观测天文条件下的搜星速度和实时输出星敏定姿结果,大大提高了航行过程中导航结果的精度和稳健性[2-4]。
目前,基于CNS+GNSS+INS的数据融合算法研究较多,但是大部分都是基于仿真试验数据进行的,没有进行实物验证[5-7],更没有考虑实际工程中存在以下难点:①INS长时间姿态误差累积导致其提供给CNS的粗姿态误差较大,影响星敏感器搜星快速性和天文导航精度[8-9];②系统硬件传输存在不可忽略的时间延迟。如IMU输出由于激光陀螺的去抖滤波等原因而带有毫秒级的延迟等,尤其在恶劣海况下载体处于较大机动时,这种延迟会导致天文丢星及无法搜星的情况,从而影响舰船长时间航行时导航定姿的精度和稳定性。本文针对以上实际工程问题,提出一种降低系统定姿延迟影响的CNS+GNSS+INS高精度实时导航框架和算法[10],并通过高精度转台测试,验证本文方法的精度和有效性。
1 CNS+GNSS+INS三组合滤波算法 1.1 CNS+GNSS+INS三组合状态方程由于系统对姿态精度要求较高,因此使用集中式卡尔曼融合滤波器进行处理,并将状态估计结果反馈至惯性导航系统内部。本文设计了状态量维数为21维的卡尔曼滤波器,其最优估计参数由IMU的误差状态构成[11],表示如下
 (1)
(1) 式中,δrn、δvn和ψ分别为惯性导航位置误差、速度误差和姿态旋转误差在导航坐标系下的投影;bg、sg分别表示陀螺零偏和比例因子;ba、sa分别表示加速度计零偏和比例因子。
采用Psi角模型[12]建立惯性导航误差模型如下
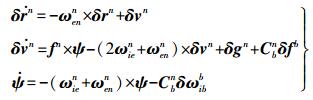 (2)
(2) 式中,n表示导航坐标系;i表示惯性坐标系;e表示地心地固坐标系;b系表示载体坐标系。
将高精度激光惯导的零偏和比例因子误差模型考虑为一阶高斯-马尔科夫过程[13]
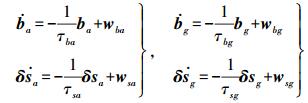 (3)
(3) 式中,wba和wsa分别表示加速度计零偏和比例因子的驱动白噪声;wbg和wsg分别表示陀螺的零偏和比例因子的驱动白噪声;τba和τsa分别表示加速度计零偏和比例因子误差的相关时间;τbg和τsg分别表示陀螺零偏和比例因子误差的相关时间。
通过上述式(2)和式(3),结合估计的误差状态量式(1),建立卡尔曼滤波的离散化状态方程如下
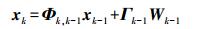 (4)
(4) 式中,Φk, k-1为k-1时刻到k时刻的状态转移矩阵,表达式可以参考文献[14];xk-1和xk分别为k-1到k时刻的状态估计向量;Γk-1为系统的噪声驱动阵;Wk-1为系统状态的噪声向量。
1.2 GNSS和CNS观测方程若GNSS数据可用时,以INS位置结果和GNSS位置结果之差δzr作为观测向量,er为位置观测噪声向量。当CNS数据可用时,有INS预测的姿态与CNS输出姿态结果之差δzΦ,eΦ为姿态观测噪声,得到基于Psi角模型的位置和姿态量测方程[15]
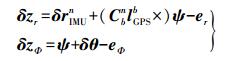 (5)
(5) 式中,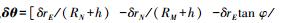
由式(5)可得其位置与姿态的观测模型为
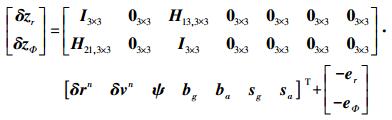 (6)
(6) 式中, H13, 3×3=Cbn(lGPSb×);
1.3 针对CNS解算中INS数据时间延迟的处理在船载基准系统运行过程中,天文系统搜星所需要的姿态是实时姿态估计,不应有延时。而由于系统设计实现的多种相关原因,提供给天文系统的姿态信息带有不可忽略的时间延迟,包括惯导的IMU输出由于激光陀螺的去抖滤波等原因而带有大约10ms的延迟、惯导数据的解算延迟等,实测总延迟约20.5ms。在海况较为恶劣时,假设船体的摇摆幅值为6°,周期15s,此时由时间延迟造成CNS接收到的惯组姿态误差最大可以达到3′,使星跟踪器接收到的用于隔离载体姿态运动的角度跟踪指令不能有效反映当前时刻载体的运动情况,无法实现有效的载体运动隔离,星跟踪器跟踪到位后,恒星无法稳定地出现在相机的视场范围内,造成天文系统无法搜星。
因此,在解算得到GNSS+INS组合姿态、位置结果时,对导航结果作外推处理后再发送给天文系统实现星敏相机对某个恒星的观测。以航向姿态φ为例,具体外推采用线性外推方案如下(等角速度外推)
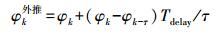 (7)
(7) 式中,φk外推为在当前k历元外推到无延迟的航向姿态;φk为当前k时刻的解算航向姿态;φk-τ为k-τ时刻历元的航向姿态;τ为设置外推到时间间隔;Tdelay为实际延迟时间。本文延迟时间为20.5ms,τ设置为15ms。
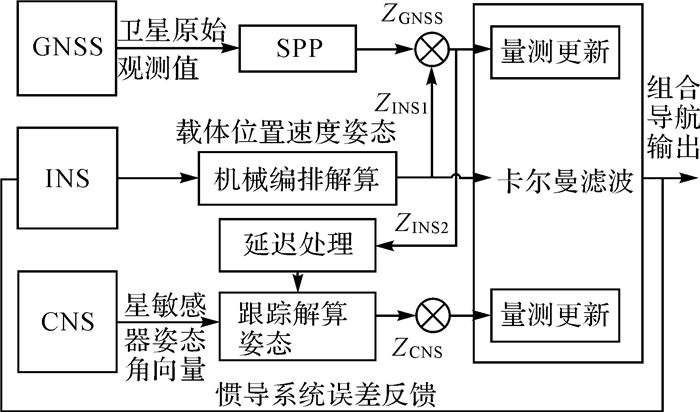
2 系统框架设计本文设计的CNS+GNSS+INS信息融合定姿框架如图 1所示。
|
| 图 1 CNS+GNSS+INS信息融合定姿框架 |
以INS作为核心,采用集中卡尔曼滤波器进行三组合导航测量。卫星、天文导航结果用于抑制惯性导航误差积累,同时实时修正惯导的误差,以提高系统的稳健性。当天文导航因观测条件限制而无法使用时,通过卫星和惯性组合的方式保障短时间段内航姿测量精度和方位测量精度,实现可持续性的定位测姿。另外,由于系统硬件(激光陀螺的去抖滤波)和传输处理所带来的延迟,GNSS+INS子滤波器输出给CNS的姿态有延时,本文对该姿态进行等角速度外推补偿后再发送给CNS使用,这样可以有效解决在舰船处于较大动态时CNS容易丢星不工作的情况,从而增加CNS系统的抗干扰能力。CNS实现高精度姿态测量后,在卡尔曼主滤波器中与INS数据进行融合,从而输出三组合的高精度姿态估计值。
3 试验结果与分析本文试验中采用的INS设备为高精度激光陀螺(性能参数参见表 1),采样率为1000Hz,输出载体的加速度和角速度信息;GNSS设备选用Trimble AG332 GPS接收机,采样率为1Hz,输出天文的位置信息;CNS设备由光学镜头、测星相机组件等组成(性能参数参见表 2),输出被测星体脱靶量数据及Camlink数字视频图像。
| 性能参数 | 数值 |
| 加速度零偏/(m·s-2) | 0.00003 |
| 速度随机游走/(m·s-1·h-1/2) | 0.00075 |
| 陀螺零偏/(°/h) | 0.002 |
| 角速度随机游走/(°·h-1/2) | 0.0005 |
为了验证该系统的实时定姿精度,实测试验需要将设备安装在姿态精度在角秒级别的高精度转台上进行,转台外环转动对应着设备的航向角变化,内环转动对应着设备的横滚角变化。测试现场如图 2所示。

|
| 图 2 测试现场 |
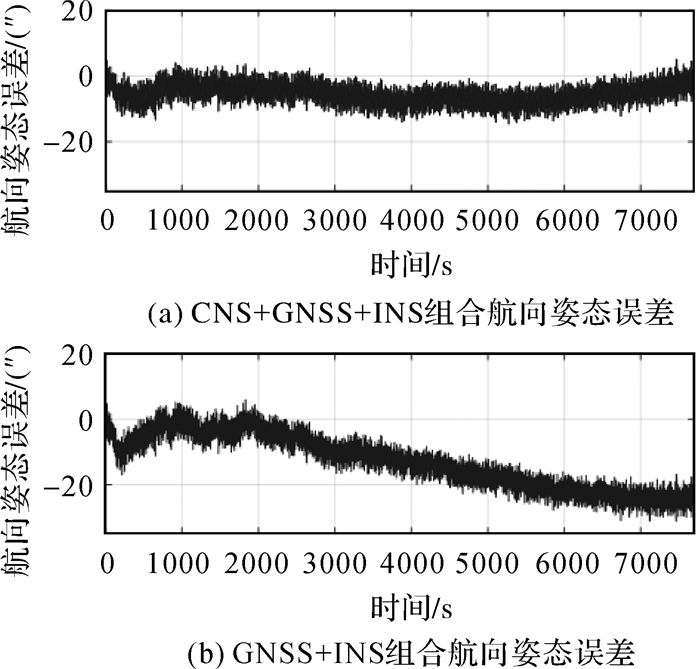
为验证CNS+GNSS+INS三组合算法的有效性,将设备安装到高精度转台上进行测试,试验测试时间为7700s,测试环境为开阔且晴朗的天空,在此期间GNSS和CNS均正常工作。设置摇摆台外环以幅值6°,周期15s。为保障试验环境的一致性,在组合导航解算程序中设置一个独立的进程来实时解算GNSS+INS组合的姿态结果,并以高精度转台的姿态输出作为参考真值,来评估三组合算法高精度实时定姿的性能。由于转台外环主要针对设备的Z轴进行旋转测试,测试过程中设备的横滚角与俯仰角动态变化过小,GNSS+INS组合与CNS+GNSS+INS组合解算结果差异不明显,因此本文试验主要对设备输出的航向姿态误差进行分析,两种组合方式得到的航向姿态误差如图 3所示。
|
| 图 3 CNS+GNSS+INS三组合与GNSS+INS两组合航向姿态误差对比 |
从图 3中可以看出,使用CNS+GNSS+INS组合方式的姿态误差曲线范围明显稳定在±10″以内,航向姿态没有漂移。使用GNSS+INS组合方式的姿态误差曲线有明显的漂移,在2h后约漂移30″。分析表 3中统计结果可知,三组合方式中CNS的加入有效抑制了航向发散,航向误差平均值为-0.619″,均方根为5.572″,明显优于GNSS+INS组合结果。
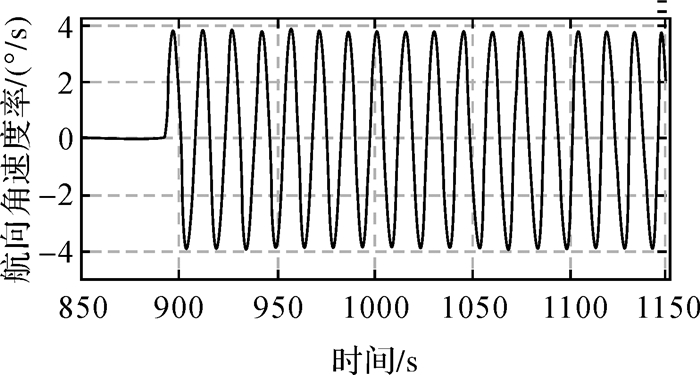
为验证INS延迟处理的效果,本文利用高精度转台进行了两次测试。第一次测试使用无INS延迟处理的程序(方案1),测试时间为16000s,测试环境为开阔且晴朗的天空,先静止设备约15min之后摇摆台外环一直以幅值6°,周期10s进行大角速率摇摆来模拟载体复杂机动环境。由于摇摆测试时间较长,截取测试开始后850~1150s的转台外环摇摆角度变化图,如图 4所示。第二次测试使用本文给出的改进INS延迟的程序(方案2),其余测试条件与第一次测试保持一致。两次测试试验各以每次试验高精度转台的姿态输出作为参考真值,来评估三组合算法进行INS延迟处理后实时定姿的性能,得到两者结果对比如图 5所示。图 5(a)为未进行延迟处理(方案1)的CNS+GNSS+INS航向姿态误差结果,(b)为进行延迟处理后(方案2)的CNS+GNSS+INS航向姿态误差结果,表 4为方案1与方案2的航向误差统计结果。
|
| 图 4 截取部分时段的转台外环摇摆角速度变化 |

|
| 图 5 有无延时处理的CNS+GNSS+INS航向姿态误差对比结果 |
分析以上图表可以看出:未进行延迟处理的三组合在开始转台静止的15min内航向误差稳定,转台外环转动后则出现了航向姿态发散,误差均值高达16.116″,均方根为19.488″。这是因为在大角速率摇摆下,惯导提供的姿态角延时不能忽略不计,此时星敏感器接收到的用于隔离载体姿态运动的角度跟踪指令不能有效反映当前时刻载体的运动情况,无法实现有效的载体运动隔离,导致恒星无法稳定地出现在相机的视场范围内,CNS无法稳定正常的工作。此时,无外推的三组合退化为GNSS+INS两组合结果,航向姿态误差逐渐积累。而在同样的摇摆条件下,加入延迟处理的三组合航向姿态误差得到了有效的控制,误差一直稳定在10″以内,均值为-4.762″,均方根为6.587″,满足高精度姿态测量需求。
4 结语本文在GNSS+INS组合导航基础上,加入CNS的星敏姿态信息对惯导进行姿态修正,设计和实现了一套CNS+GNSS+INS三组合定位定姿架构和算法,以满足船载测量任务对高精度姿态信息的需求。针对恶劣海况下CNS+GNSS+INS三组合系统中,因INS的硬件延迟、计算延迟等造成的CNS搜星和跟星不稳定问题,提出了一种对INS预测姿态进行等角速度外推的处理方法。最后利用高精度转台模拟载体复杂运动环境,对该系统进行了实测验证评估。试验结果表明:引入INS姿态外推方法能够有效维持星敏相机连续稳定工作,保障了三组合定位定姿系统的姿态精度和稳定性。
| [1] |
WU X, WANG X. A SINS/CNS deep integrated navigation method based on mathematical horizon reference[J]. Aircraft Engineering and Aerospace Technology, 2011, 83(1): 26-34. DOI:10.1108/00022661111119892 |
| [2] |
GREWAL M S, WEILL L R, ANDREWS A P. Global positioning systems, inertial navigation, and integration[M]. 2nd ed. New York: John Wiley & Sons, 2007.
|
| [3] |
BRITTING K R. Inertial navigation systems analysis[M]. New York: John Wiley & Sons, 1971.
|
| [4] |
TITTERTON D, WESTON J.捷联惯性导航技术[M].张天光, 王秀萍, 王丽霞, 等, 译. 2版.北京: 国防工业出版社, 2007: 18-20.
|
| [5] |
李艳华, 房建成, 贾志凯. INS/CNS/GPS组合导航系统仿真研究[J]. 中国惯性技术学报, 2002, 10(6): 6-11. DOI:10.3969/j.issn.1005-6734.2002.06.002 |
| [6] |
吴坤峰, 杨峰, 梁彦, 等. INS/GPS/CNS组合导航系统仿真[J]. 火力与指挥控制, 2010, 35(7): 13-15. DOI:10.3969/j.issn.1002-0640.2010.07.004 |
| [7] |
张科, 刘海鹏, 李恒年, 等. SINS/GPS/CNS组合导航联邦滤波算法[J]. 中国惯性技术学报, 2013, 21(2): 226-230. DOI:10.3969/j.issn.1005-6734.2013.02.019 |
| [8] |
BARBOUR N. Inertial navigation sensors[R]. Cambridge: Charles Stark Draper Laboratory, 2011.
|
| [9] |
张亚男, 张震, 赵桂玲, 等. 移动测量平台在线对准方法研究[J]. 测绘通报, 2015(8): 4-8. |
| [10] |
马宏阳, 程鹏飞, 黄华东. GPS/INS位置、速度和姿态全组合导航系统研究[J]. 测绘通报, 2016(3): 10-14. |
| [11] |
SHIN E.Estimation technique for low-cost inertial navigation[D]. Calgary: University of Calgary, 2005.
|
| [12] |
BENSON D O. A comparison of two approaches to pure-inertial and doppler-inertial error analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 1975, AE S-11(4): 447-455. |
| [13] |
PARK M. Error analysis and stochastic modeling of MEMS based inertial sensors for land vehicle navigation applications[D]. Calgary: University of Calgary, 2004.
|
| [14] |
牛小骥, 王强, 李由, 等. 利用伪观测取代精密转台的原地旋转调制寻北[J]. 中国惯性技术学报, 2015, 23(6): 707-713. |
| [15] |
DMITRIYEV S P, STEPANOV O A, SHEPEL S V. Non-linear filtering methods applications in INS alignment[J]. IEEE Transaction on Aerospace and Electronic Systems, 1997, 33(1): 260-272. DOI:10.1109/7.570762 |