2. 中国科学院空天信息研究院, 北京 100094
2. Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China
惯性导航系统是一种自主式的导航系统。其优点是可提供连续的导航信息,短期的定位精度和稳定性好,但是由于导航信息是由积分产生,定位误差随时间而增大,不能长期独立工作,而多源融合导航方法则可以有效弥补惯性导航系统的缺点。传统的方法是采用惯导+卫星组合导航方法[1-3]来修正惯导累积误差,但是在大型仓库、地下停车场、城市地下交通路网等室内、地下等卫星信号薄弱的场景中该方法就不再适用。而视觉导航方法在光源充足、纹理特征点丰富的条件下具有精度高、稳定性好、可靠性高等优点,并且在室内场景中效果同样很好[4]。但是视觉导航方法计算复杂度较高,有时不能保持连续性。利用惯导的短时连续性可以提高视觉导航方法中的匹配搜索效率,因此视觉与惯导组合定位[5]具有广阔的发展前景。
本文研究的INS+视觉组合的定位方法中,采用基于合作目标[6]的单目视觉定位方法,主要作用是修正惯性导航系统的姿态、位置积累误差,从而提高整个系统的导航精度。视觉定位系统首先获取含有编码标志的图像,提取其中的特征信息,由对应编码获得其在参考坐标系中的坐标,继而得到自身的位姿信息,最后采用基于卡尔曼滤波[7]的方法将惯导的导航信息与视觉的位姿信息进行融合处理,实现对惯导误差的修正。
对于惯导误差的修正方法,传统方法是采用直接位置校正方法[8-15],即检测到惯导系统的误差后,直接更改导航解算过程中的位姿数据,这种方法不能有效抑制位置误差曲线的增长。为了解决这一问题,本文利用视觉定位的位姿信息建立观测方程,进行卡尔曼滤波,并通过分析算法实际应用场景,选用合适的试验设备,进行实际试验对比验证了该算法对惯导系统误差的修正具有良好的效果,同时也具有一定的工程参考价值。
1 基于合作目标的单目视觉定位本文采用的视觉定位方法是基于合作目标的单目视觉定位方法,主要原理为:采用附有编码标志图片的人工标志物作为定位的合作目标。首先在室内场景(如走廊、地下车库)的墙顶、侧墙面等位置每隔一定距离布置并固定人工标志物,该标志物为人工编码且具有唯一编码的标志卡片,用单目相机对标志物进行连续拍照后完成该场景中人工标志物的建模,即获得每个人工标志物在该相对参考系中的坐标。之后在融合定位的过程中,每当单目相机收到信号进行拍照获得含有编码标志的图像,就提取其中的特征点信息,由对应编码获得其在参考坐标系中的坐标,继而计算得到相机自身的位姿信息。
这种基于合作目标的单目视觉定位方法输出的具体参数有相机自身的姿态角(横滚角、俯仰角、偏航角)以及三轴坐标位置(x, y, z)。视觉定位求解相机自身位姿信息的基本原理为摄影测量中的空间后方交会求解外方位元素,其基本解算步骤为:
(1) 确定平均摄影距离(大概航高)、内方位元素、编码标志的空间坐标及对应的像点坐标。
(2) 确定相机位置的初值及相机姿态的初值。
(3) 对每个编码标志点,依次计算出像点坐标的近似值。
(4) 求解相机姿态与位置未知量的误差,与对应的近似值相加,可得未知量的近似值。
(5) 当所求误差小于规定阈值时,停止迭代。
本文的惯导+视觉组合算法,即利用上述介绍的视觉定位方法来获取视觉定位结果,以对惯导进行修正。
另外,通过利用惯导的短时连续定位结果,可以优化视觉定位中搜索匹配算法的计算复杂度。具体来说,由前一时刻惯导定位的结果推算出当前时刻惯导的相对位置,进一步推导出编码标志在相片上像点坐标的大概位置,以这个位置为中心进行一定范围的窗口搜索,即可提高编码标志识别的搜索效率。
2 惯导+视觉组合算法本文的惯导+视觉组合算法采用卡尔曼滤波算法,利用视觉定位获得的姿态和位置信息对整个系统的误差进行估计,并修正惯导系统的位姿误差,降低姿态和位置误差的变化率,从而提高惯导定位精度。
为了描述惯导系统的运动参数,本文主要用到两个参考坐标系,分别为载体坐标系和导航坐标系。其中,载体坐标系采用右前上坐标系,导航坐标系采用东北天地理坐标系。
2.1 导航状态变量算法选取18维状态变量为
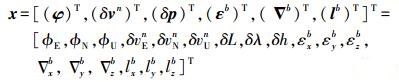 (1)
(1) 式中,ϕE、ϕN、ϕU为姿态角误差;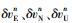
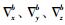
姿态的误差方程为
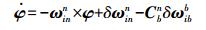 (2)
(2) 式中,ωinn=ωien+ωenn;Cbn为从载体坐标系到导航坐标系的方向余弦矩阵(DCM)。
2.2.2 速度误差方程速度的误差方程为
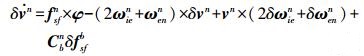 (3)
(3) 式中,fsfb为载体坐标系上的加速度计比力。
2.2.3 位置误差方程位置的误差方程为
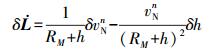 (4)
(4) 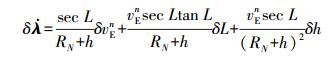 (5)
(5) 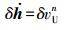 (6)
(6) 由以上误差方程可得,整个系统的状态方程为
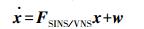 (7)
(7) 式中,FSINS/VNS为系统状态矩阵;w为预测噪声向量(均值为零,方差为Q的白噪声)。相应的预测噪声协方差矩阵Q为
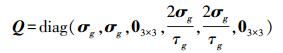 (8)
(8) 式中,σg、σa为陀螺仪、加速度计随机游走误差,σg=diag(σgx2, σgy2, σgz2),σa=diag(σax2, σay2, σaz2)。
系统状态矩阵FSINS/VNS按下式计算[16]
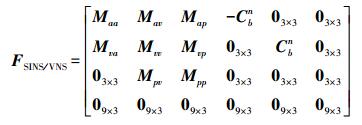 (9)
(9) 其中,每个子块按如下方式计算
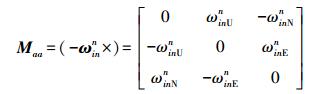 (10)
(10) 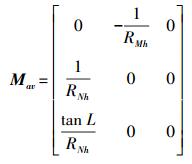 (11)
(11) 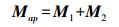 (12)
(12) 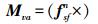 (13)
(13) 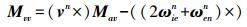 (14)
(14) 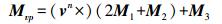 (15)
(15) 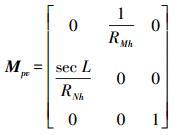 (16)
(16)  (17)
(17) 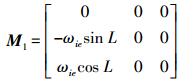 (18)
(18)  (19)
(19) 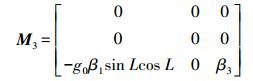 (20)
(20) 式中,ωie为地球角速率,ωie=7.2921151467×10-5rad/s;Re为地球半长轴,Re=6378137m;g0为赤道海平面的重力加速度,g0=9.7803267714m/s2;β1=5.27094×10-3;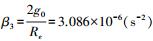
算法选取惯导系统与视觉系统的姿态、位置之差作为观测量z,即
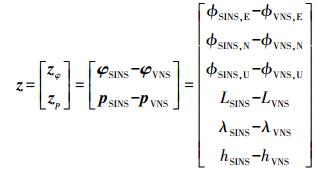 (21)
(21) 系统量测方程为
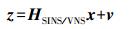 (22)
(22) 式中,HSINS/VNS为系统量测矩阵;v为观测噪声向量(均值为零,方差为R的白噪声),相应的观测噪声协方差矩阵为
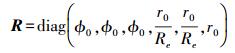 (23)
(23) 式中,ϕ0、r0为提前确定的姿态、位置观测噪声。系统量测矩阵HSINS/VNS按下式计算
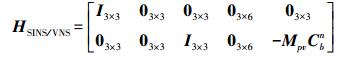 (24)
(24) 每次观测量的值更新后,得到当前误差估计的最优值,利用该值对惯导的当前位姿信息进行反馈修正。
3.1 姿态的修正采用的修正方程为
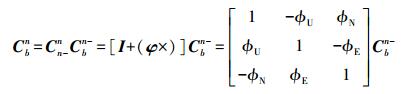 (25)
(25) 式中,Cbn-为惯导系统解算出的方向余弦矩阵;Cbn为修正后的更精确的方向余弦矩阵,由Cbn可以计算出更精确的姿态角。
3.2 速度、位置的修正采用的修正方程为
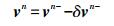 (26)
(26) 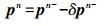 (27)
(27) 式中,vn-、pn-分别为惯导系统解算出的速度、位置向量;δvn-、δpn-分别为滤波器估计的速度、位置误差向量;vn、pn分别为修正后的更精确的速度、位置向量。
4 试验验证为了验证本文所提出的惯导位姿修正方法,在地下车库进行了试验验证。地下车库已经事先布置好编码标志并完成建模,对应地下车库中的一块方形区域,南北方向的两条通道布满了编码标志,而东西方向的两条通道则没有布置编码标志。每个编码标志对应唯一的编码序列,并且确定了每个编码标志在同一个参考坐标系下的三维坐标,可以直接进行基于合作目标的单目视觉定位。
该试验主要使用一台手推车作为载体放置试验设备,试验设备包括一台笔记本电脑,安装有时间同步软件、惯导记录软件、视觉定位软件及组合定位算法Matlab程序,一台MTI惯导和一台单目视觉相机分别与电脑连接以采集原始数据,100C与接收机连接作为轨迹基准。试验开始时,首先对惯导系统和相机进行对准,然后设定相机触发频率,在0.2Hz的条件下绕地下车库两周进行定位试验以检验惯导精度。
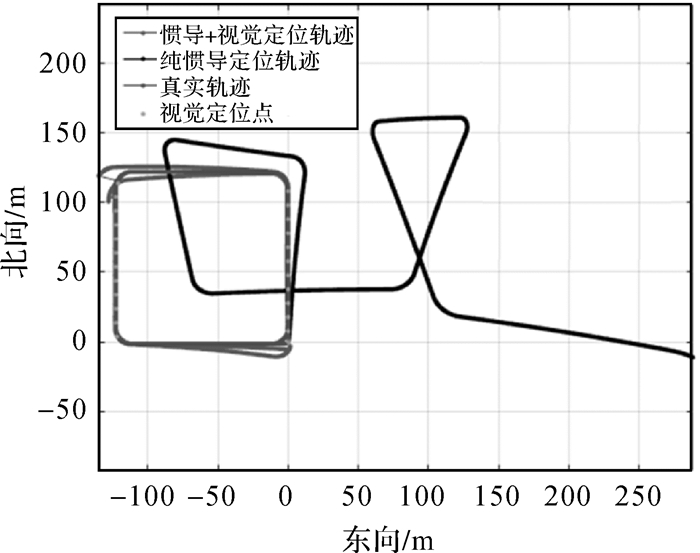
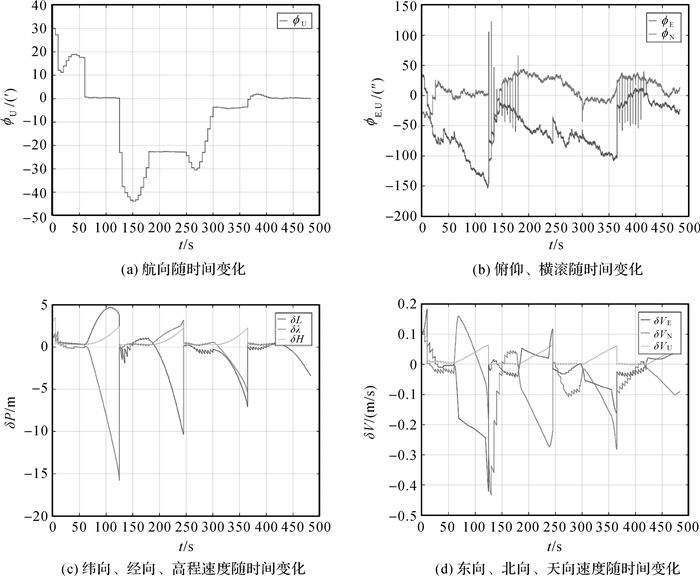
在地下车库中整个系统的运动轨迹如图 1所示,惯导+视觉组合算法的误差曲线如图 2所示。
|
| 图 1 系统运动轨迹及参数 |
|
| 图 2 惯导+视觉算法的误差曲线 |
由系统的误差曲线图 2可知,经过惯导+视觉组合算法对惯导系统的位姿修正后,整个系统的姿态、速度、位置误差都较小;横滚角、俯仰角误差最后稳定在2角分以内,偏航角误差最后稳定在10角分以内;东向、北向、天向速度最后都稳定在0.1m/s以内;纬度、经度误差最后稳定在2m以内,高度误差最后稳定在5m以内。同时,各误差曲线均逐渐呈收敛趋势,由于算法采用闭环反馈修正的形式,因此,误差曲线在一定的误差范围内呈现出振荡趋势,这也说明了该算法的优越性。
由图 1可知,纯惯导定位轨迹的累计误差会随时间而变得很大,纯视觉定位结果虽然精度较高,但却不能保持连续性,而相较之下惯导+视觉组合定位轨迹与真实轨迹呈逐渐贴合趋势,说明该导航结果能满足一般需求。
改变相机触发频率,分别在0.2Hz、0.1Hz、不触发的条件下进行试验,其他条件不变,仍然绕地下车库一周进行定位试验,在每种频率各进行3次试验,对比几次试验的结果见表 1。
| 试验次数 | 偏航角误差/(′) | 位置误差/m | ||||
| 触发频率/Hz | 0.2 | 0.1 | 不触发 | 0.2 | 0.1 | 不触发 |
| 1 | 3.6 | 11.4 | 27.3 | 1.0 | 3.3 | 198.7 |
| 2 | 6.9 | 16.2 | 26.4 | 2.2 | 3.2 | 334.4 |
| 3 | 10.1 | 21.3 | 28.1 | 1.3 | 4.1 | 257.5 |
由表 1可知,对于相同的一次试验,相机不同的触发频率会导致导航结果的误差不同,并且触发频率越高,导航结果的误差越小,因此在考虑计算成本与相机硬件限制的前提下,采用0.2Hz的触发频率效果最好;同时,有触发相机进行修正时的导航结果误差明显小于不触发相机进行修正时的误差,说明本算法对惯导误差的修正具有良好的效果。
5 结论本文针对在室内场景中卫星信号薄弱导致惯导+卫星组合导航方法不再适用的问题,提出了一种新的基于惯导+视觉组合的室内惯导位姿修正方法,主要工作可以总结为:①分析基于合作目标的单目视觉定位原理,并利用其定位结果建立惯导系统姿态误差、位置误差的量测方程对惯导系统的位姿进行修正;②在特定室内场景中选取符合相应应用场景的试验设备多次进行试验验证算法的有效性与优越性。试验结果表明,本文提出的修正算法能够有效解决室内场景中惯导位姿误差的修正问题,具有良好的效果且具有一定的工程参考价值。
| [1] |
HE X F. Application of interval Kalman filter to an integrated GPS/SINS system[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 1999, 16(1): 39-45. |
| [2] |
ZHANG J, XU X, WANG B. A system-level compensation method for inertial navigation system[J]. Lecture Notes in Electrical Engineering, 2012, 176(4): 229-233. |
| [3] |
郝雨时, 徐爱功, 隋心, 等. 噪声协方差自适应控制下的双天线GNSS/INS初始对准方法[J]. 测绘学报, 2018, 47(4): 473-479. |
| [4] |
王勇, 陈国良, 李晓园, 等. 一种相机标定辅助的单目视觉室内定位方法[J]. 测绘通报, 2018(2): 35-40. |
| [5] |
徐勇志, 宁晓琳. 一种巡视器惯性/视觉组合导航新方法[J]. 空间科学学报, 2015, 35(6): 721-729. |
| [6] |
倪立学, 徐贵力, 胡建华. 一种地面合作目标的研究与设计[J]. 光电工程, 2007, 34(7): 8-13. DOI:10.3969/j.issn.1003-501X.2007.07.002 |
| [7] |
BASS R W. Kalman filtering:theory and practice[J]. Proceedings of the IEEE, 1996, 84: 321-321. DOI:10.1109/JPROC.1996.482233 |
| [8] |
LI L Z, WANG X H, CAI S J. New recursion formula used in the matrix of the direction cosine in the strapdown inertial navigation and guidance system[J]. Journal of Astronautics, 2006, 27(3): 349-353. |
| [9] |
HENDY H, RUI X T, KHALIL M. An integrated GPS/INS navigation system for land vehicle[J]. Applied Mechanics and Materials, 2013, 336-338(1): 221-226. |
| [10] |
MUSOFF H, MURPHY J H. Study of strapdown navigation attitude algorithms[J]. Journal of Guidance Control Dynamics, 2012, 18(2): 287-290. |
| [11] |
SAVAGE P G. Strapdown inertial navigation integration algorithm design part 1:attitude algorithms[J]. Journal of Guidance Control & Dynamics, 1998, 21(1): 19-28. |
| [12] |
SAVAGE P G. Strapdown inertial navigation integration algorithm design part 2:velocity and position algorithms[J]. Journal of Guidance Control & Dynamics, 1998, 22(2): 384-384. |
| [13] |
ROGERS R M, ROGERS R, ROGERS C R. Applied mathematics in integrated navigation systems[J]. Reston American Institute of Aeronautics & Astronautics Inc., 2007(2): 78-88. |
| [14] |
TITTERTON D, WESTON J. Strapdown inertial navigation technology[J]. IEEE Aerospace & Electronic Systems Magazine, 2005, 20(7): 33-34. |
| [15] |
YU J C, CHEN J B, XU X Q. Multi-position observability analysis of strapdown inertial navigation system[J]. Journal of Beijing Institute of Technology, 2004, 24(2): 150-153. |
| [16] |
BORTZ J E. A new mathematical formulation for strapdown inertial navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1971, AES-7(1): 61-66. DOI:10.1109/TAES.1971.310252 |


