2. 中国测绘科学研究院, 北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China
随着社会经济的发展,用户对于大型商场、办公区域、机场、博物馆等室内环境的精确的基于位置的服务(location based service, LBS)需求越来越大[1],从而多种室内定位方法应运而生,如WiFi、射频识别(RFID)、超宽带(UWB)、蓝牙等无线定位技术[2],以及地磁、超声波、视觉、惯性导航等非无线定位技术[3]。现如今,无线定位技术已有许多应用案例,UWB可以实现厘米级的定位精度[4],基于WiFi信号接收强度(RSSI)的指纹定位精度可达到1~5m,蓝牙天线阵列和指纹识别定位分别可达到 < 1m和2~5m的精度[5]。其中,UWB和蓝牙天线阵列技术需要专属的设备,且价格昂贵,推广难度大[6];与前两者相比,蓝牙和WiFi基站的价格相对低廉,在推广应用上有巨大的优势。与WiFi相比,蓝牙基站有如下优势:内置电池(2~3年寿限),可以通过设置发射功率调节蓝牙信号覆盖范围(覆盖半径为10~100m),而且蓝牙技术已经广泛集成于移动设备中,更加易于推广使用。因此,蓝牙室内定位成为当前适用性最佳的技术之一[7]。
基于低成本设备的蓝牙定位中,其算法以基于RSSI的蓝牙指纹识别为主,最常见的有最近邻法、K最近邻法和贝叶斯算法[8]。其中,最近邻算法和K最近邻算法简单,易于实现,但是定位精度较低;贝叶斯算法的定位精度优于近邻算法[9]。然而,贝叶斯算法将每个参考点的先验概率视为等值[10],在动态定位过程中,前一定位结果会影响后续定位中参考点的先验概率[11],并且先验概率对定位有很强的约束性[12],因此贝叶斯算法的等值先验概率在动态定位中不适用。对于该问题,许多研究人员提出在参数学习中融入先验知识,即加入约束条件[13]。文献[14]采用动态位置先验概率,通过最短距离矩阵确定参考点的先验概率,该算法平均定位误差达到1.82m;文献[15]将确定性算法和概率性算法相融合,利用近邻算法筛选参考点,定位准确率比最近邻算法提高了4%;文献[16]将各区域建模以确定先验信息,在基站密度为30m2/个时,误差在2.6m的可信度为95%。
在动态定位中,距离参数和航向参数都是重要的先验条件,基于此,本文提出一种贝叶斯定位改进算法。该算法在贝叶斯指纹算法的基础上,引入陀螺仪的航向信息[17],并利用航向信息对高斯核函数模型[18]进行改进,以改进模型作为投票算法来确定先验概率;先验概率结合实时RSSI计算位于参考点上的后验概率,选取前n个概率最高的点,以概率为权重加权平均得到待测点坐标。
1 贝叶斯指纹算法离线采集阶段,在定位区域以一定间隔布设参考点,使用采集设备在每个参考点同时采集n个iBeacon的主机唯一识别码(universally unique identifier,UUID)、信号强度RSSI,并计算每个基站在对应参考点的信号强度均值μ、标准偏差σ。以上数据结合已知的参考点坐标构成位置指纹库L
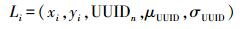 (1)
(1) 同一位置的RSSI分布可以近似用高斯概率分布来描述[19],因此,其概率密度函数可以近似表示为
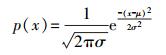 (2)
(2) 式中,x表示定位过程中接收到的信号强度值;μ表示信号强度的均值;σ表示信号强度的标准偏差。
在线定位阶段,贝叶斯估计根据贝叶斯和全概率公式,由先验概率计算后验概率。定位区域内有N个参考点,坐标分别为Zi=(xi, yi),RSSIi为参考点i的指纹数据。待测点实时信号强度为S(RSSI1,RSSI2,…,RSSIn)时,定位在参考点i的概率为
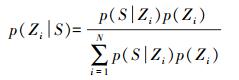 (3)
(3) 式中,p(Zi)为先验概率,贝叶斯算法将先验概率p(Zi)视为等值。利用参考点RSSI的均值和标准差通过式(3)计算信号指纹为S时定位在参考点i的概率,选取概率最高的n个参考点,计算待测点的最或然值。
2 改进的贝叶斯算法由于动态定位过程中,前一定位结果会影响到后续定位中参考点的先验概率,因此贝叶斯算法的等值先验概率不适用。本文借助高斯核函数模型(式(4))的概率约束性,以及利用陀螺仪获取的航向信息建立投票算法,计算参考点先验概率。
 (4)
(4) 陀螺仪是智能手机必备的传感器,可为用户提供方向信息。基于陀螺仪数据的常用航向获取方法有欧拉角法、方向余弦法和四元数法。相对比其他两个方法,四元数法具有计算量少、易于操作,并且能避免出现欧拉角法中“奇点”问题的优点,故本文选择四元数法来解算航向信息。利用四元数法获取陀螺仪航向信息的方法详见文献[17],主要过程如下:利用二阶龙格库塔法更新解算四元数q(q0,q1,q2,q3)
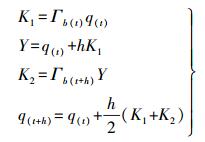 (5)
(5) 获取到实时的四元数信息后,即可推算出航向信息θ
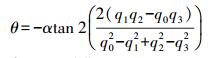 (6)
(6) 由式(6)得到运动航向θ,人为设定检索上限角度α,本文设定α为45°。根据这两个参数确定一个扇形区域作为参考点的检测区域,通过改进的高斯核函数(式(7))计算该区域内的参考点的投票概率g(x, y),作为参考点的先验概率。
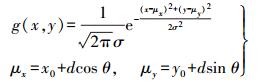 (7)
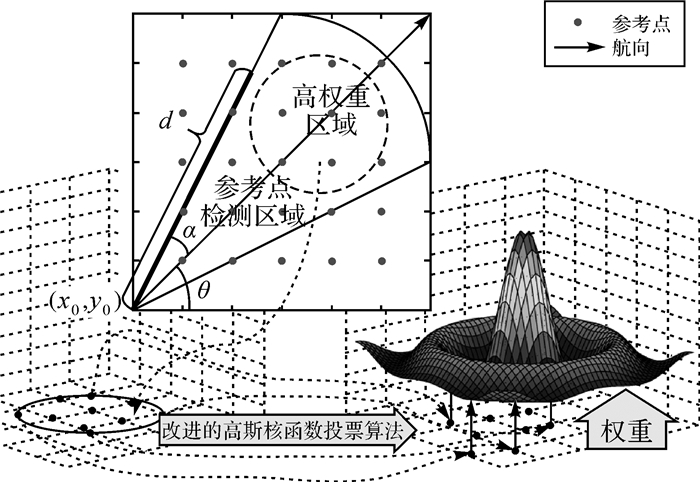
(7) 式中,(x0, y0)为前一点的坐标;d为单位时间的平均移动距离。本文d的初始值设定为0.9m,计算得到待测点位置后,实时对d进行更新。改进的高斯核函数为模型的投票算法如图 1所示。
|
| 图 1 投票算法说明 |
通过改进高斯核函数,放大了投票中心的参考点的先验概率,使待测点近邻区域的参考点拥有较大的先验概率。
2.3 待测点计算流程在线定位阶段,根据接收到的信号强度S(RSSI1,RSSI2,…,RSSIn)计算待测点定位在每个参考点的后验概率p(Zi|S),并将式(7)得到的先验概率g(Zi)代入式(3),得
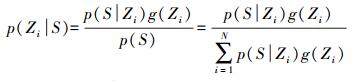 (8)
(8) 式中,Zi表示参考点的位置Z(xi, yi);g(Zi)则表示待测点在点Zi处的先验概率,可由式(7)积分求得;p(S|Zi)表示信号强度为S时,待测点在Zi处的概率。由于各个基站的信号强度相互独立[20],故p(S|Zi)可以用联合概率分布函数来描述
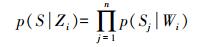 (9)
(9) 最后,取前m个概率最大的参考点(本文中设置m=4),以概率作为权重,加权平均求得待测点最或然值
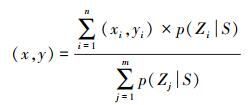 (10)
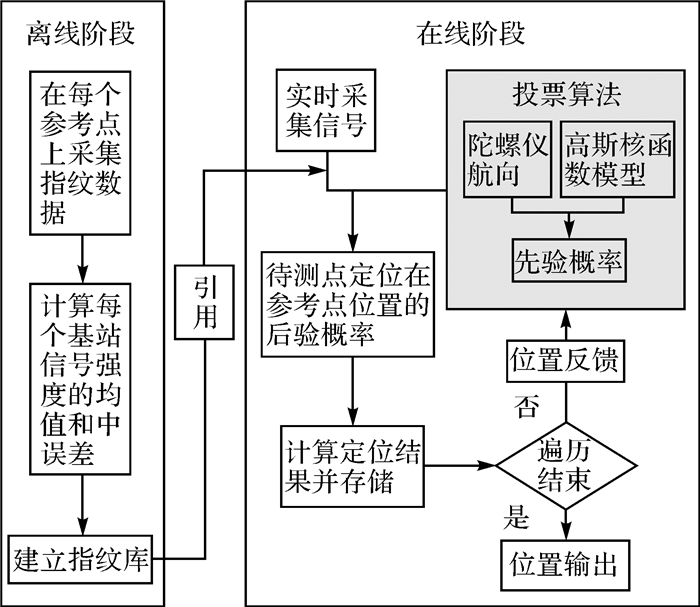
(10) 本文改进算法的核心是确定先验概率的投票算法。在离线阶段采集参考点指纹信息;在线阶段,由航向信息确定某一检索区域,再利用改进的高斯投票算法计算检索区域参考点的先验概率,根据实时信号强度计算参考点的后验概率;以概率定权,前m个概率最大的参考点坐标的加权平均作为定位结果。算法的具体流程如图 2所示。
|
| 图 2 算法流程 |
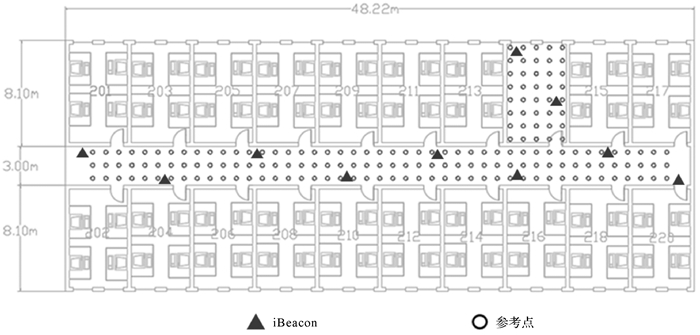
贝叶斯指纹定位算法需要在离线阶段建立指纹库,本文选用的iBeacon可持续发射信号强度为-100~-50dBm的信号。为完成指纹的采集工作,编写了能够采集信号强度、主机号、识别码的APP,采集界面如图 3所示。试验场地位于山东科技大学测绘科学与工程学院S2实验楼二楼走廊区域,圆点表示参考点(如图 4所示),其间隔为1m,总共175个参考点。试验者手持智能手机分别在每个参考点位置采集参考点指纹信息(每个基站的信号强度、iBeacon主机号、识别码),采集频率为1Hz,每个点持续采集60s,分别计算采集到的信号强度的均值和中误差。

|
| 图 3 数据采集界面 |
|
| 图 4 参考点及基站的分布 |
设置试验对改进算法的精度进行测试:在参考点布设区域设置长120m的闭合试验路线,试验者手持采集设备,按设计路线走,实时采集陀螺仪数据和蓝牙数据;分别用本文的改进算法和贝叶斯算法对该数据进行处理,对得到的两种结果进行比较。
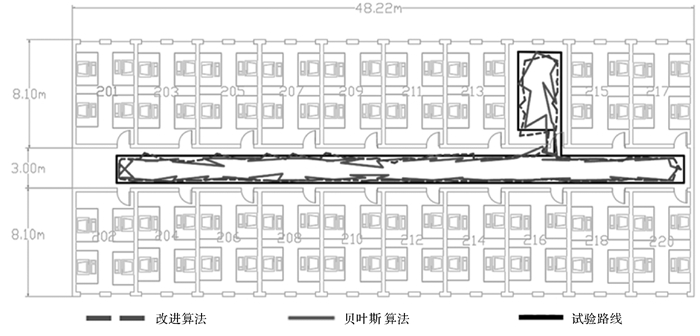
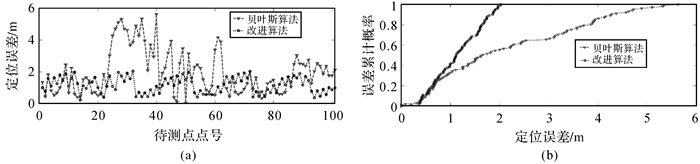
为了从整体上比较这两种算法,分别计算两种算法的定位路线(如图 5所示),定位误差(如图 6(a)所示)和误差概率累计函数(如图 6(b)所示),并将各类参数进行统计(见表 1)。本文将平均点位误差、最大定位误差和误差累计概率作为衡量精度的标准。
|
| 图 5 定位路线 |
|
| 图 6 点位误差及误差累计概率函数 |
| 算法 | 误差累计概率/(%) | 平均误差/m | 最大误差/m | |||
| 1m | 2m | 3m | 4m | |||
| 贝叶斯算法 | 30.3 | 50.8 | 61.1 | 76.2 | 2.17 | 5.83 |
| 改进算法 | 42.9 | 96.1 | 100 | 100 | 1.15 | 2.09 |
从图 5看出,与贝叶斯算法相比,本文算法明显改善了定位过程中位置跳变、“后退”的现象。由图 6及表 1的测试结果可得,在动态定位方面,本文算法明显优于原始算法。贝叶斯算法的平均定位误差为2.17m,误差在1m和2m内的可信度分别为30.3%和50.8%;而改进算法的平均定位误差为1.15m,定位误差在1m和2m内的可信度分别为42.9%和96.1%;改进算法最大定位误差为2.09m,原始算法最大误差高达5.83m。
3.2.2 试验2为了进一步对本文提出的算法进行测试,在走廊区域设置长50m的复杂变向路线(包括三角形、弧形线路),比较改进算法和原始算法的定位结果,以此来检验算法在复杂路径的适用性和稳健性,本试验将平均定位误差和定位标准差作为衡量标准;同时,提取试验路线的近邻点,每次提取4个距离最近的点及其后验概率P,分别计算两算法的近邻点与对应点的信息熵[21],信息熵越大,近邻点的概率离散程度越大。以信息熵为衡量标准验证投票算法的性能。信息熵计算方法如下
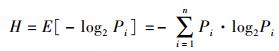 (11)
(11) 式中,Pi为第i个近邻点的后验概率。
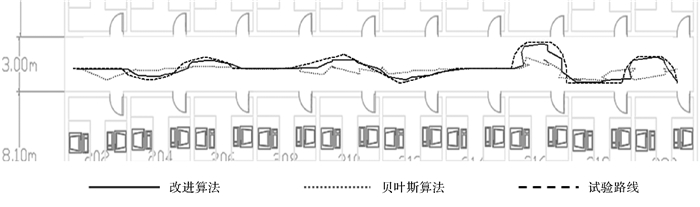
两算法的复杂路线定位路线如图 7所示,定位误差和累计概率如图 8所示,信息熵如图 9所示, 各项衡量参数见表 2。
|
| 图 7 定位路线效果 |
|
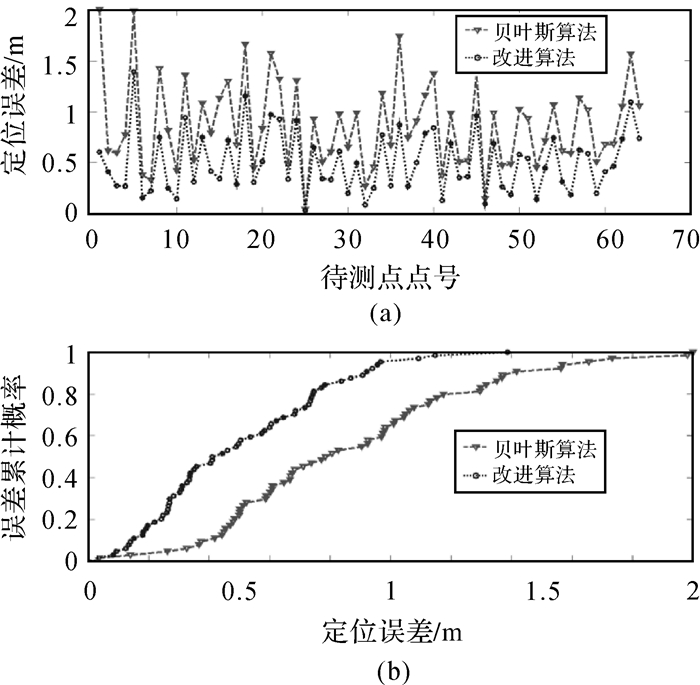
| 图 8 点位误差及误差累计概率 |
|
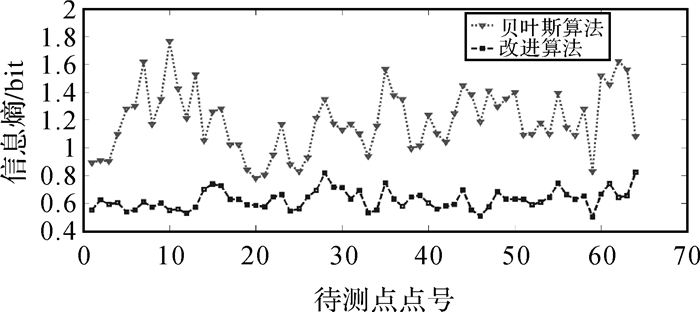
| 图 9 近邻点信息熵对比 |
| 算法 | 误差累计概率/(%) | 平均定位误差/m | 标准偏差/m | 平均信息熵/bit | ||
| 1m | 2m | 3m | ||||
| 贝叶斯算法 | 64.7 | 98.4 | 100 | 0.86 | 1.26 | 1.19 |
| 改进算法 | 94.8 | 100 | 100 | 0.50 | 0.42 | 0.63 |
从图 7可以看出,改进算法的定位路线的定位效果更佳;由图 8和表 2可得,复杂路径试验中,改进算法的平均定位误差为0.50m,点位误差的极差和标准偏差分别为1.30和0.24m,与贝叶斯算法相比,定位误差降低了41.9%,标准偏差减少了1.02m。因此,通过综合考虑定位精度、定位偏差及误差累计分布情况,改进算法优于原始算法并且具有较强的稳健性。从图 9可得,改进算法的整体信息熵小于原始算法对应的值,表 2中改进算法的平均信息熵比原始算法低0.56bit,故投票算法所得的先验概率对参考点有更好的约束性,且有利于定位。
4 结语本文提出了一种基于蓝牙的贝叶斯指纹改进算法,利用陀螺仪获取的航向信息和高斯核函数模型,建立先验概率投票算法,将先验概率权重集中在待测点近邻区域,提高了先验概率对定位范围的约束,提高了定位精度。与贝叶斯指纹算法相比,该定位算法的平均定位误差有明显的下降;在不规则路线定位中,本文算法展现了较好的精度和稳健性。后续工作为减少算法的运行时间,进一步提高算法的实时性。
| [1] |
PETROVA K, WANG B. Location-based services deployment and demand:a roadmap model[J]. Electronic Commerce Research, 2011, 11(1): 5-29. |
| [2] |
AOMUMPAI S, KONDEE K, PROMMAK C, et al. Optimal placement of reference nodes for wireless indoor positioning systems[C]//Proceedings of the 11th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology. Nakhon Ratchasima: IEEE, 2014: 1-6.
|
| [3] |
CHOW J C K, PETER M, SCAIONI M, et al. Indoor tracking, mapping, and navigation:algorithms, technologies, and applications[J]. Journal of Sensors, 2018(4): 1-3. |
| [4] |
YIN Z, JIANG X, YANG Z, et al. WUB-IP:a high-precision UWB positioning scheme for indoor multiuser applications[J]. IEEE Systems Journal, 2018. |
| [5] |
陈锐志, 陈亮. 基于智能手机的室内定位技术的发展现状和挑战[J]. 测绘学报, 2017, 46(10): 1316-1326. DOI:10.11947/j.AGCS.2017.20170383 |
| [6] |
席瑞, 李玉军, 侯孟书. 室内定位方法综述[J]. 计算机科学, 2016, 43(4): 1-6, 32. |
| [7] |
MA Z, POSLAD S, BIGHAM J, et al. A BLE RSSI ranking based indoor positioning system for generic smartphones[C]//Proceeding of 2017 Wireless Telecommunications Symposium. Chicago: IEEE, 2017: 1-8.
|
| [8] |
JANICKA J, RAPINSKI J. Application of RSSI based navigation in indoor positioning[C]//Proceedings of 2016 Baltic Geodetic Congress. Gdansk: IEEE, 2016.
|
| [9] |
DAVIDSON P, PICHÉ R. A survey of selected indoor positioning methods for smartphones[J]. IEEE Communications Surveys and Tutorials, 2017, 19(2): 1347-1370. DOI:10.1109/COMST.2016.2637663 |
| [10] |
曹鸿基, 汪云甲, 毕京学, 等. 一种顾及用户朝向的加权贝叶斯指纹定位方法[J]. 测绘科学, 2018, 43(9): 103-107, 114. |
| [11] |
游康勇, 杨立山, 刘玥良, 等. 基于稀疏贝叶斯学习的网格自适应多源定位[J]. 电子与信息学报, 2018, 40(9): 2150-2157. |
| [12] |
O'HAGAN A, LEONARD T. Bayes estimation subject to uncertainty about parameter constraints[J]. Biometrika, 1976, 63(1): 201-203. DOI:10.1093/biomet/63.1.201 |
| [13] |
FEELDERS A, GAAG L C. Learning Bayesian network parameters under order constraints[J]. International Journal of Approximate Reasoning, 2006, 42(1): 37-53. |
| [14] |
邵剑飞, 叶阿勇. 基于位置连续性的室内定位算法[J]. 福建师范大学学报(自然科学版), 2015, 31(3): 17-25. |
| [15] |
王忠民, 陈振, 潘春华. 一种改进的位置指纹智能手机室内定位算法[J]. 西安邮电大学学报, 2014, 19(1): 17-20. |
| [16] |
FARAGHER R, HARLE R. Location fingerprinting with bluetooth low energy beacons[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(11): 2418-2428. DOI:10.1109/JSAC.2015.2430281 |
| [17] |
郭英, 姬现磊, 刘清华, 等. 基于手机陀螺仪航向修正算法[J]. 中国惯性技术学报, 2017, 25(6): 719-724. |
| [18] |
王双成, 高瑞, 杜瑞杰. 基于高斯Copula的约束贝叶斯网络分类器研究[J]. 计算机学报, 2016, 39(8): 1612-1625. |
| [19] |
ZAFARI F, PAPAPANAGIOTOU I, HACKER T J. A novel Bayesian filtering based algorithm for RSSI-based indoor localization[C]//Proceedings of 2018 IEEE International Conference on Communications. Kansas City: IEEE, 2018.
|
| [20] |
CHEN Z, ZHU Q, SOH Y C. Smartphone inertial sensor-based indoor localization and tracking with iBeacon corrections[J]. IEEE Transactions on Industrial Informatics, 2016, 12(4): 1540-1549. DOI:10.1109/TII.2016.2579265 |
| [21] |
龙英, 何怡刚, 张镇, 等. 基于信息熵和Haar小波变换的开关电流电路故障诊断新方法[J]. 仪器仪表学报, 2015, 36(3): 701-711. |


