2. 甘肃省地理国情监测工程实验室, 甘肃 兰州 730070;
3. 中国测绘科学研究院, 北京 100830
2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China;
3. Chinese Academy of Surveying and Mapping, Beijing 100830, China
随着移动通信技术及定位技术的迅速发展,移动目标数据库(moving object database, MOD)已经成为数据库领域近几年来研究的热点问题[1]。MOD作为表示移动目标及其位置信息的数据库在民航管制、交通管理、军事指挥、基于位置的信息服务等众多领域有着广泛的应用,但同时如何对移动目标存储、检索和位置管理等技术成为建设数据库所面临的新挑战[2]。MOD的存储和管理空间数据必然离不开空间关系分析,而空间拓扑关系作为空间关系的一个重要内容,它的研究将直接影响MOD的建设。
在空间拓扑关系描述模型研究中,比较常用的是文献[3]提出的基于拓扑关系点集理论描述框架的4元组模型(4-intersection model, 4IM)和9交模型(9-intersection model, 9IM)。同时,国内外学者针对4IM和9IM描述空间拓扑关系的不足也作了很多研究,如文献[4]提出维数的概念,定义了不同相交情况对应不同维数,得到维数扩展模型DE-4IM和DE-9IM;文献[5]在9IM的基础上,通过嵌套矩阵的模式区分各种空间对象之间的拓扑关系;文献[6]利用空间对象之间、对象内部之间和对象边界之间的相互运算,提出新的4元组模型(4IDM);文献[7]利用空间对象Voronoi区域来替换它在9IM中的外部,提出了基于Voronoi图的9交模型。同时还有学者提出不同的模型,如文献[8]提出了空间代数模型来描述空间拓扑关系。
虽然以上模型对空间关系描述作了很多详细的研究,但是基本上都是对空间拓扑关系的形式化描述,忽略了空间目标的度量特性。从而没有足够的细节对空间关系进行重要区分,得到的空间关系为粗略的空间关系分类,使其拓扑关系容易受误差和不确定性的影响,并很难满足动态信息分析和提取的需要[9]。为此一些学者也进行了空间拓扑关系度量化描述[10-11]及动态目标拓扑关系描述[12-14]的研究,尽管取得一些成果,但都是对静态特定空间目标间的拓扑度量化描述和对动态目标间的拓扑形式化描述,并没有将二者结合在一起,导致动态目标缺少细节上度量描述。
因此,本文基于格网化的思想[15],通过引入内部分量、边界分量、外部分量等3种度量参数对移动目标空间拓扑关系进行度量描述。
1 9交模型9交模型是Egenhofer(1990)[3]以点集拓扑学为理论基础, 在4交模型区分线与线、线与面两类空间对象不足的情况下,提出的一种拓扑关系描述框架[16]。它将任何一个空间对象(A)划分成边界(∂A)、内部(A0)和外部(A-) 3个部分,并通过这3部分点集的交进行拓扑关系区分。这样对于任意的两个空间对象间的拓扑关系描述可表示成9种情况,每种情况的取值分为空(Φ)或非空(¬Φ)两种值,如下所示
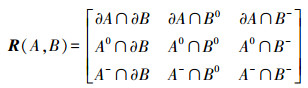 (1)
(1) 9交模型是对空间目标拓扑关系的形式化描述,因此它的分类为粗略的分类,它所描述的拓扑关系只是拓扑关系的类别。
2 目标格网化及确定拓扑关系对于传统空间目标的拓扑关系判定都是利用矢量数据,通过求解矢量点、线、面交的方式,其计算量大。因此本文通过格网化的思想进行求解,首先将对象划分为固定大小的格网阵列,然后利用9交模型判定各个格网相交情况对空间拓扑关系进行形式化描述。
2.1 目标对象的格网化为了更好地表达和计算空间关系,本文定义点目标为一个格网,线目标为一系列连续点目标构成的格网链,面目标为一条首尾相接的线目标构成的封闭区间格网面,如图 1所示。每个格网都由量化的横纵坐标表示其位置,并通过动态调整格网大小,保证目标边界格网唯一性,使边界对应的格网只能表示一个目标对象的边界。
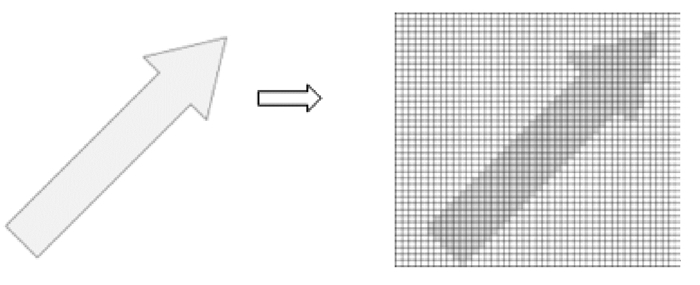
|
| 图 1 空间目标的格网化 |
目标内部、边界、外部对应格网位置的存储采用单向链表的方式进行存储,定义链表Boundary_List存储边界格网;链表Interior_List存储内部格网;链表Exterior_List存储外部格网。其中,点状目标的边界格网链表和内部格网链表相同,线状目标的边界格网链表为线目标两端点格网位置,以方便后面计算。
2.2 确定拓扑关系通过上面的格网化,点、线、面等空间对象均被描述为一个或多个格网阵列,然后借助9交模型的定性描述,判断边界格网链表、内部格网链表和外部格网链表等链表是否含有相同数据元素值来确定拓扑关系,即判断空间目标边界、内部、外部是否有交集。本文将拓扑关系形式化描述主要分为:相等关系(equal)、相离关系(disjoint)、相接关系(touch)、相交关系(overlap)和包含关系(contain)等5种关系。
3 目标空间拓扑关系度量描述9交模型中空间对象之间的拓扑关系通过内部、边界和外部的相互作用来描述。因此,对于内部、边界和外部交的度量是拓扑关系的度量描述的关键。本文引入内部分量、边界分量、外部分量对空间对象内部、边界和外部进行细化的度量描述。
3.1 内部分量空间对象内部有相交情况一般为拓扑包含、拓扑相交和拓扑相接等关系,而在连续变化的空间目标为拓扑相交时,9交模型就难以有效的形式化描述空间关系,如图 2所示,在t1、t2、t3、t4时刻,拓扑形式化描述都为相交关系,但是在空间对象A的内部相交面积在不断地发生变化。

|
| 图 2 连续变化的空间目标拓扑关系 |
因此,本文引入内部分量二元组(OA,OB)对空间目标内部情况进行度量描述,通过计算参考目标内部格网相交点数占参考目标内部所有格网数的比重和占对象目标所有格网的比重得到。OA和OB计算公式为
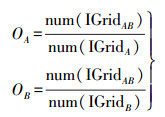 (2)
(2) 式中,num(IGridAB)表示参考目标A内部相交重叠的格网数,包括目标B边界与目标A内部相交的格网数和目标B内部与目标A内部相交的格网数;num(IGridA)和num(IGridB)分别表示目标A的内部所有格网数和目标B的所有格网数(包括边界格网数和内部格网数)。OA和OB的取值范围[0, 1],当拓扑关系为相离时两个值取值均为0;当拓扑关系为包含时OA的取值为(0, 1),OB的取值为1;当拓扑关系为相交时两个值取值均为(0, 1);当拓扑关系为相接时两个值取值均为[0, 1);当拓扑关系为相等时OA的取值为1,OB的取值为(0, 1)。
3.2 边界分量对于拓扑相接和相交关系,边界相交部分的大小及相交特征等的度量描述是区别于其他拓扑关系的一个重要因素。因此,本文引入边界分量二元组(TA, TB)对空间目标边界情况进行度量描述,通过计算参考目标边界格网相交点数占参考目标边界所有格网数的比重和占对象目标所有格网的比重得到。TA和TB计算公式为
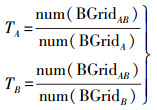 (3)
(3) 式中,num(IGridAB)表示参考目标A边界相交重叠的格网数,包括目标A和B边界相交格网数和目标B内部与目标A边界相交格网数;num(IGridA)和num(IGridB)分别表示目标A的边界所有格网数和目标B的所有格网数(包括边界格网数和内部格网数)。TA和TB的取值范围[0, 1],当拓扑关系为包含或相离时两个值取值均为0;当拓扑关系为相等时TA的取值为1,TB的取值为(0, 1);当拓扑关系为相接时两个值取值均为[0, 1];当拓扑关系为相交时取值为[0, 1)。
3.3 外部分量在9交模型中,空间对象的外部为除去空间对象自身以外的所有二维空间,其范围太大,直接对外部度量描述比较困难。因此,本文引入外部分量Dmin通过计算两目标边界格网间最小距离的格网数进行度量描述。Dmin的计算公式
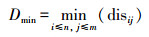 (4)
(4) 式中,n、m分别表示目标A、B边界格网数;i、j分别表示目标A、B边界中任意一个格网;disij表示目标A边界上第i个格网与目标B边界上第j个格网间的格网数。在计算含有线状目标外部分量时,由于线目标的边界为两端点,不能完全表达外部的内边界,因此,在计算过程中线状目标边界格网由自身的内部格网和边界格网构成。
3.4 移动目标拓扑关系度量表达移动目标是空间与时间耦合框架下的统一体,其位置或形状会随时间的变化而变化[18]。因此,移动目标拓扑的度量需要一个静止的目标对象作为参考目标;同时,在某一时间段内移动目标相对于参考目标的拓扑关系可以由时间段内连续时间点的拓扑关系组合描述。本文通过引入时间变量T并利用有序三元组Top(A, B, T)的形式来度量描述移动目标的拓扑关系,即
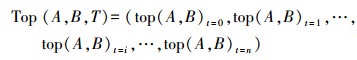 (5)
(5) 式中,A表示参考目标;B表示移动目标;Top(A, B, T)表示移动目标B相对于参考目标A在时间段T内的拓扑关系;top(A, B)t=i表示在t=i时刻移动目标相对于参考目标的拓扑度量描述,计算公式为
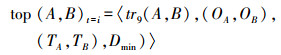 (6)
(6) 式中,tr9(A, B)表示目标A、B拓扑关系形式化描述,即基于9交模型的拓扑关系;(OA,OB)、(TA,TB)和Dmin分别表示目标A、B的内部分量、边界分量和外部分量。
4 试验与分析试验分为两组,分别是以线状目标和面状目标为参考目标,对点、线、面状移动目标进行拓扑度量分析。如图 3所示,图 3(a)—(c)组参考目标为线状目标,图 3(d)—(f)组为面状目标;图 3中(a)和(d)、(b)和(e)、(c)和(f)组分别表示移动点目标、线目标、面目标的拓扑关系描述。图中浅色表示目标边界,深色表示相交格网。表 1表示了图 3中每组移动目标在t1、t2、t3、t4、t5时刻拓扑度量描述;表 2表示了图 3中每组移动目标在时间段T=[t1, t5]内的拓扑度量描述。
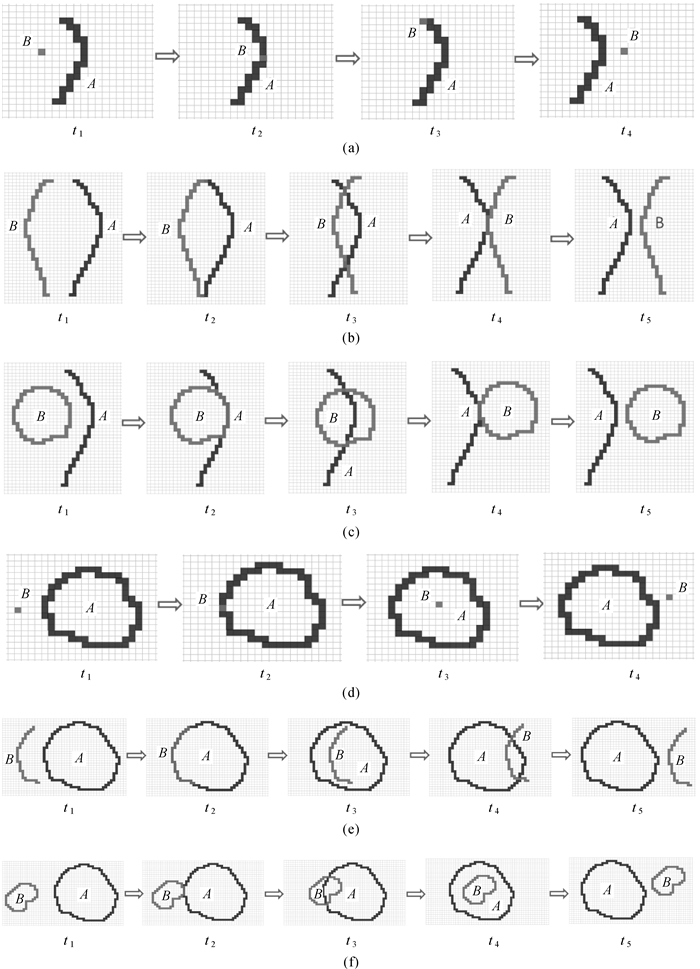
|
| 图 3 移动目标拓扑关系度量描述 |
| top(A, B)t=i | t1 | t2 | t3 | t4 | t5 |
| a | 〈disjoint,(0, 0),(0, 0),3〉 | 〈contain,(0.02, 1),(0, 0),0〉 | 〈touch,(0, 0),(0.5, 1),0〉 | 〈disjoint,(0, 0),(0, 0),4〉 | |
| b | 〈disjoint,(0, 0),(0, 0),5〉 | 〈touch,(0, 0),(1, 0.041),0〉 | 〈overlap,(0.102, 0.102),(0, 0),0〉 | 〈touch,(0.102, 0.102),(0, 0),0〉 | 〈disjoint,(0, 0),(0, 0),2〉 |
| c | 〈disjoint,(0, 0),(0, 0),4〉 | 〈touch,(0.408, 0.085 9),(0, 0),0〉 | 〈overlap,(0.489 8, 0.103),(0, 0),0〉 | 〈touch,(0.122 4, 0.026),(0, 0),0〉 | 〈disjoint,(0, 0),(0, 0),2〉 |
| d | 〈disjoint,(0, 0),(0, 0),3〉 | 〈touch,(0, 0),(0.019, 1),0〉 | 〈contain,(0.009, 1),(0, 0),0〉 | 〈disjoint,(0, 0),(0, 0),2〉 | |
| e | 〈disjoint,(0, 0),(0, 0),5〉 | 〈touch,(0, 0),(0.342, 1),0〉 | 〈contain,(0.073 4, 1),(0, 0),0〉 | 〈overlap,(0.041 4, 0.564),(0.035, 0.103),0〉 | 〈disjoint,(0, 0),(0, 0),3〉 |
| f | 〈disjoint,(0, 0),(0, 0),7〉 | 〈touch,(0, 0),(0.044, 0.03),0〉 | 〈overlap,(0.089, 0.435),(0.035, 0.287),0〉 | 〈contain,(0.309, 1),(0, 0),0〉 | 〈disjoint,(0, 0),(0, 0),3〉 |
时间点t1、t2、t3、t4、t5通常选择拓扑关系或度量参数发生变化的时刻。在表 1中a(t1)、a(t4)、b(t1)、b(t5)、c(t1)、c(t5)、d(t1)、d(t4)、e(t1)、e(t5)、f(t1)、f(t5)为拓扑相离时,内部分量和边界分量的取值均为(0, 0),边界分量取值为两目标边界间最小格网数,在其他拓扑关系中,边界分量取值均为0;在表 1中a(t3)、b(t2)、b(t4)、c(t2)、c(t4)、d(t2)、e(t2)、f(t2)为拓扑相接时,内部分量OA和OB的取值范围为[0, 1),边界分量TA和TB的取值范围为[0, 1];在表 1中b(t3)、c(t3)、e(t1)、e(t4)、f(t3)为拓扑相交时,内部分量OA和OB的取值范围为(0, 1),边界分量TA和TB的取值范围为[0, 1);在表 1中a(t2)、e(t3)、f(t4)为拓扑包含时,内部分量OA的取值为(0, 1),OB的取值为1,边界分量TA和TB的取值为0;这些取值范围不考虑两目标相互缠绕的情况。在表 1组别b的t2、t4时刻,拓扑关系形式化描述都为相接关系,通过内部变量和边界变量的计算,可以看到t2时刻是线、线对象边界相接,内部没有相交(OA, OB)=(0, 0),t4时刻是线、线对象内部相接,边界没有相交(TA, TB)=(0, 0);t3、t4时刻,线拓扑关系形式化描述分别为相交关系和相接关系,由于参考目标内部相交格网相同都为5,所有内部分量和边界分量相同。因此,利用拓扑形式化和度量化描述相结合的方法能够更加有效、准确地描述空间目标间拓扑关系。表 2中,将具有代表性时间点的拓扑度量描述有序的组合在一起描述移动目标相对于参考目标的拓扑变化,使得移动目标的拓扑关系描述更加直观和详细。
| 组别 | Top(A, B, T) |
| a | (〈disjoint,(0, 0),(0, 0),3〉,〈contain,(0.02, 1),(0, 0),0〉,〈touch,(0, 0),(0.5, 1),0〉,〈disjoint,(0, 0),(0, 0),4〉) |
| b | (〈disjoint,(0, 0),(0, 0),5〉,〈touch,(0, 0),(1, 0.041),0〉,〈overlap,(0.102, 0.102),(0, 0),0〉,〈touch,(0.102, 0.102),(0, 0),0〉,〈disjoint,(0, 0),(0, 0),2〉) |
| c | (〈disjoint,(0, 0),(0, 0),4〉,〈touch,(0.408, 0.085 9),(0, 0),0〉,〈overlap,(0.489 8, 0.103),(0, 0),0〉,〈touch,(0.122 4, 0.026),(0, 0),0〉,〈disjoint,(0, 0),(0, 0),2〉) |
| d | (〈disjoint,(0, 0),(0, 0),3〉,〈touch,(0, 0),(0.019, 1),0〉,〈contain,(0.009, 1),(0, 0),0〉,〈disjoint,(0, 0),(0, 0),2〉) |
| e | (disjoint,(0, 0),(0, 0),5〉,〈touch,(0, 0),(0.342, 1),0〉,〈contain,(0.073 4, 1),(0, 0),0〉,〈overlap,(0.041 4, 0.564),(0.035, 0.103),0〉,〈disjoint,(0, 0),(0, 0),3〉) |
| f | (〈disjoint,(0, 0),(0, 0),7〉,〈touch,(0, 0),(0.044, 0.03),0〉,〈overlap,(0.089, 0.435),(0.035, 0.287),0〉,〈contain,(0.309, 1),(0, 0),0〉,〈disjoint,(0, 0),(0, 0),3〉) |
本文基于格网化的思想,首先将对象目标和参考目标格网化,然后利用9交模型对空间目标的拓扑关系进行形式化描述,最后引入内部分量、边界分量、外部分量对拓扑关系进行细化度量描述,使得拓扑关系描述更加详细;在描述移动目标拓扑关系时通过引入时间变量,利用有序三元组Top(A, B, T)的形式来度量描述。通过试验分析,该方法计算简单、直观,能更加有效、详细地度量移动目标间的拓扑关系的。在接下来的工作中,将对复杂空间拓扑关系度量描述和不确定性空间对象拓扑度量描述进行研究。
| [1] |
WOLFSON O, XU B, CHAMBERLAIN S, et al. Moving objects databases: issues and solutions[C]//International Conference on Scientific and Statistical Database Management. Capri: IEEE Computer Society, 1998: 111-122. https://www.researchgate.net/publication/3758116_Moving_objects_databases_Issues_and_solutions
|
| [2] |
于秀兰, 陈滢, 丁晓诚, 等. 一种基于道路网络的移动目标数据库模型[J]. 软件学报, 2003, 14(9): 1600-1607. |
| [3] |
EGENHOFER M, FRANZOSA R. Point-set topological spatial relations[J]. International Journal of Geographical Information Systems, 1991, 5(2): 161-174. DOI:10.1080/02693799108927841 |
| [4] |
CLEMENTINI E, FELICE P D, OOSTEROM P V. A small set of formal topological relationships suitable for end-user interaction[C]//International Symposium on Advances in Spatial Databases. Singapore: Springer-Verlag, 1993: 277-295. https://link.springer.com/chapter/10.1007%2F3-540-56869-7_16?LI=true
|
| [5] |
KURATA Y. The 9+-intersection: a universal framework for modeling topological relations[C]//International Conference on Geographic Information Science. Berlin: Springer-Verlag, 2008: 181-198. https://link.springer.com/chapter/10.1007%2F978-3-540-87473-7_12
|
| [6] |
邓敏, 李志林, 李永礼, 等. GIS线目标间拓扑关系描述的4交差模型[J]. 武汉大学学报(信息科学版), 2006, 31(11): 945-948. |
| [7] |
CHEN Jun, LI Chengming, LI Zhilin, et al. A voronoi-based 9-intersection model for spatial relations[J]. International Journal of Geographical Information Systems, 2001, 15(3): 201-220. DOI:10.1080/13658810151072831 |
| [8] |
LI Zhilin, ZHAO R, CHEN J. A voronoi-based spatial algebra for spatial relations[J]. Progress in Natural Science:Materials International, 2002, 12(7): 50-58. |
| [9] |
邓敏, 李成名, 刘文宝. 利用拓扑和度量相结合的方法描述面目标间的空间关系[J]. 测绘学报, 2002, 31(2): 164-169. DOI:10.3321/j.issn:1001-1595.2002.02.014 |
| [10] |
王珂, 张周威. 矢栅一体化拓扑关系的度量描述研究[J]. 武汉大学学报(信息科学版), 2015, 40(5): 638-643. |
| [11] |
吴长彬, 闾国年. 线面拓扑和度量关系的细分描述和计算方法[J]. 计算机辅助设计与图形学学报, 2009, 21(11): 1551-1557. |
| [12] |
高勇, 刘瑜, 邬伦, 等. 移动点对象与参考地物空间拓扑关系[J]. 计算机工程, 2007, 33(22): 57-59. DOI:10.3969/j.issn.1000-3428.2007.22.020 |
| [13] |
张彩丽, 吴静, 邓敏. 移动点与参考地物时空关系的自然语言描述方法研究[J]. 地理与地理信息科学, 2015, 31(3): 12-16. DOI:10.3969/j.issn.1672-0504.2015.03.003 |
| [14] |
高勇, 张晶, 朱晓禧, 等. 移动对象时空拓扑关系模型[J]. 北京大学学报(自然科学版), 2007, 43(4): 468-473. DOI:10.3321/j.issn:0479-8023.2007.04.006 |
| [15] |
罗芳, 艾廷华, 王洪. 闭合坐标链多边形数据的拓扑关系快速构建[J]. 武汉大学学报(信息科学版), 2004, 29(6): 558-561. |
| [16] |
吴华意, 刘波, 李大军, 等. 空间对象拓扑关系研究综述[J]. 武汉大学学报(信息科学版), 2014, 39(11): 1269-1276. |



