2. 中国科学院大学, 北京 100049
2. University of the Chinese Academy of Science, Beijing 100049, China
在全球卫星导航系统(global navigation satellite system, GNSS)中,星载原子钟的钟差预报在优化导航电文中的钟差参数、满足实时动态精密单点定位的需求和提供卫星自主导航所需要的先验信息方面具有重要作用[1-4]。但是,由于星载原子钟处于失重环境中,极易受到外界和自身因素的影响而很难去掌握其内部复杂细致的变化规律。因此,如何建立精确的星载原子钟运行模型就变得非常困难,如何准确预报卫星钟差也变得极其困难[5-7]。
近年来,国内外众多学者对卫星钟差预报从各个方面进行了深入广泛的研究,提出了短期、中长期和长期的卫星钟差预报方法,主要有:二次多项式模型(quadratic polynomial model, QPM)、灰色预报模型(grey model, GM(1, 1))、卡尔曼滤波模型(Kalman filter, KF)、自回归模型(autoregressive, AR(p))、自回归滑动平均模型(auto-regressive moving average, ARMA)和支持向量机模型(support vector machines, SVM)等[8-13]。这些预报方法分别适用于不同情况下导航卫星星载原子钟钟差的短期、中长期和长期的预报,但是也均有各自的适用范围和局限性。灰色预报模型适合处理数据量少、样本小、信息不全的不确定性问题,具有计算简便和抗干扰能力强等优点[14]。在应用灰色预报模型进行卫星钟差预报时,首先要确定模型的参数,参数估计的好坏程度直接影响预报结果的精确程度。然而,在估计灰色预报模型参数时一般采用的是最小二乘法,而最小二乘法是基于误差平方和最小为原则进行寻优,很容易陷入局部最小。在卫星钟频率漂移较大的情况下,应用最小二乘法估计灰色模型参数,并预报卫星钟差得到的结果会产生较大的误差。
本文针对在卫星钟频率漂移较大的情况下,应用最小二乘法估计灰色模型参数对预报卫星钟差精度的不足,采用最小一乘法估计灰色模型参数的方法。该方法在进行模型参数求解时,应用线性规划的方法对目标函数进行寻优,从理论上和方法上克服了最小二乘法估计灰色模型参数的不足,同时,将该改进方法应用到当卫星钟差波动较大情况下的钟差预报,通过试验结果的对比分析,验证该改进方法的有效性和优越性。
1 灰色预报模型在灰色系统理论中,GM(1, 1)模型是最常用的一种灰色系统模型,它是由一个仅包含单变量的一阶微分方程所构成的预报模型,适合对自身数据的预报,而且具有只需要少量数据建模等优点[15]。
设有数据序列:X(0)= {x(0)(1), x(0)(2), …, x(0)(n)},通过一次累加生成新的序列为
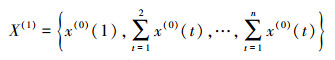 (1)
(1) 对累加序列X(1)建立一阶微分方程
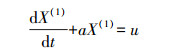 (2)
(2) 式中,a为发展系数;u为灰作用量。对式(2)离散化处理,可得矩阵方程
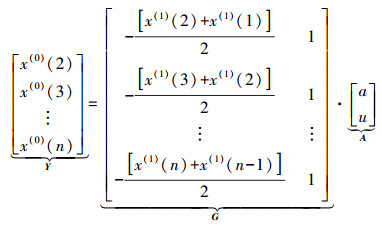 (3)
(3) 对模型参数a和u作最小二乘估计
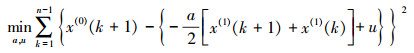 (4)
(4) 根据最小二乘法可得矩阵方程式(3)的最小二乘解为
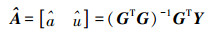 (5)
(5) 式中,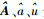
将式(5)代入式(2)得
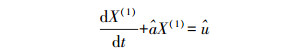 (6)
(6) 求解时间响应函数式(6)的解为
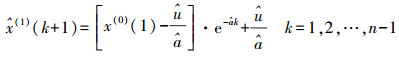 (7)
(7) 由于序列X(1)是序列X(0)的累加序列,因此原始序列X(0)的预报模型为
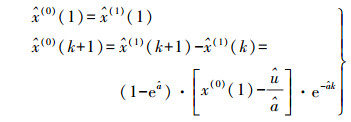 (8)
(8) 式中,k为参与预报的原始数据序列的个数。
一般形式为
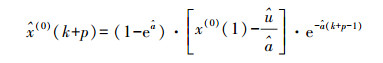 (9)
(9) 式中,p为预报点数。由以上预报模型即可对未来任意时刻的钟差数据序列进行预报。
2 基于最小一乘法改进的灰色模型的预报原理由式(4)可知,在传统灰色模型的模型参数估计中,利用的是最小二乘法,即使用的是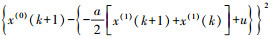
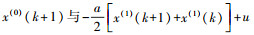
在卫星钟差预报中,部分星载原子钟由于老化频率漂移等原因,形成的卫星钟差波动也比较大。针对这种情况,在进行卫星钟差预报时,不宜使用最小二乘法去估计灰色模型的模型参数。最小一乘法利用的是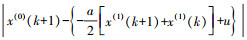
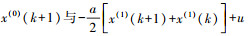
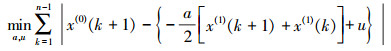 (10)
(10) 然后将利用最小一乘法估计出的模型参数代入式(9)中即可对未来任意时刻的钟差进行预报。由于优化问题式(10)的目标函数不可微,无法利用通常的方法。引入变换
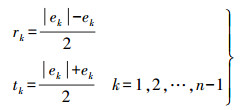 (11)
(11) 式中
从而式(10)可改写为
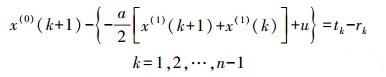 (12)
(12) 利用最小一乘法估计灰色模型的参数问题可以归结为如下的线性规划问题
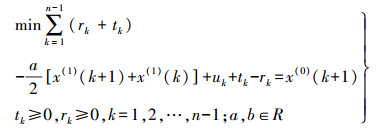 (13)
(13) 利用单纯形法[16-18]即可解上述的线性规划问题,从而可求出模型参数a和u的估计值,然后代入式(9)即可对未来任意时刻的钟差数据序列进行预报。
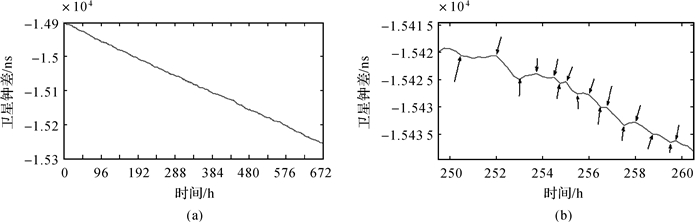
3 试验与分析 3.1 数据来源为了验证该改进方法的有效性和可行性,从IGS(International GNSS Service)服务器(ftp://cddis.gsfc.nasa.gov)上下载了2016年4月3日至9日共7 d的IGS事后精密卫星钟差产品进行预报试验,其采样间隔为15 min,即1 h记录4个历元的钟差数据。对这期间的32颗GPS卫星一周的钟差数据的波动情况进行了分析,发现PRN24(ⅡF-Cs)号卫星的钟差波动情况较大。为了说明本文改进方法对预报卫星钟差具有奇异点或钟差波动比较大时这种类型的卫星钟差预报的有效性,笔者选择了PRN24号卫星的钟差数据进行预报试验。图 1(a)为PRN24号卫星一周的钟差变化情况,图 1(b)为PRN24号卫星钟差局部放大图。
|
| 图 1 PRN24号卫星一周的钟差变化和局部放大图 |
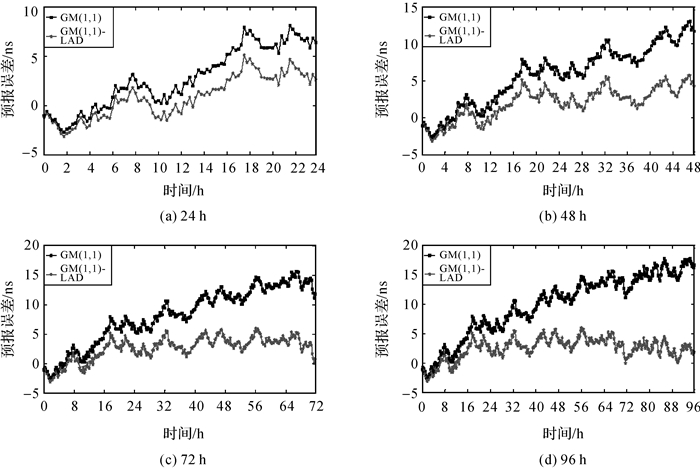
本试验采用2 h的钟差数据(2016年4月3日00:00—2016年4月3日2:00)共9个历元[14]建立灰色预报模型和基于最小一乘法改进的灰色预报模型,然后分别去预报未来10、12、14、16 h短期的钟差数据,即预报历元步长为41、49、57、65;预报未来24、48、72、96 h中长期的钟差数据,即预报历元步长为97、193、289、385,预报未来7、14、21、28 d长期的钟差数据,即预报历元步长为673、1345、2017、2689。将10、12、14、16 h的实际观测钟差数据,24、48、72、96 h的实际观测钟差数据和7、14、21、28 d的实际观测钟差数据与各模型预报的钟差数据相减即可得到预报误差。因为IGS服务器上公布的为事后钟差产品,因此钟差的自身误差小于0.1 ns,可以作为真值,使用均方根误差(RMS)(具体计算公式见式(14))作为衡量预报精度的标准,检验各模型所预报结果的好坏程度。图 2—图 4和表 1—表 3分别给出了传统灰色模型和基于最小一乘法改进的灰色模型的预报误差和预报误差的统计特性,其中MAX、MEAN分别代表最大误差和平均误差。
|
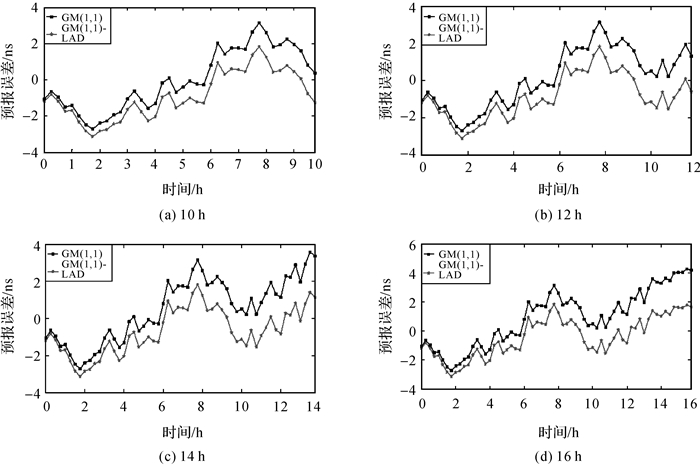
| 图 2 PRN24号卫星10、12、14、16 h短期的预报误差 |
|
| 图 3 PRN24号卫星24、48、72、96 h中长期的预报误差 |
|
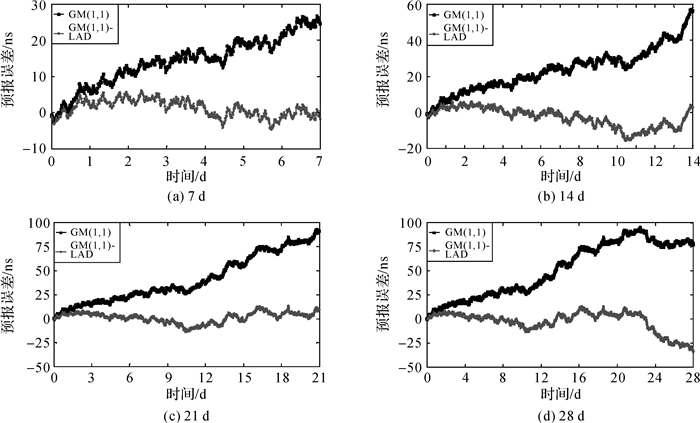
| 图 4 PRN24号卫星7、14、21、28 d长期的预报误差 |
| 步长/h | 预报方法 | MAX/ ns |
MEAN/ ns |
RMS/ ns |
| 10 | GM(1, 1) | 3.14 | 1.43 | 1.64 |
| GM(1, 1)-LAD | 3.12 | 1.35 | 1.56 | |
| 12 | GM(1, 1) | 3.14 | 1.35 | 1.57 |
| GM(1, 1)-LAD | 3.12 | 1.27 | 1.48 | |
| 14 | GM(1, 1) | 3.59 | 1.52 | 1.76 |
| GM(1, 1)-LAD | 3.12 | 1.19 | 1.41 | |
| 16 | GM(1, 1) | 4.27 | 1.81 | 2.15 |
| GM(1, 1)-LAD | 3.12 | 1.22 | 1.42 |
| 步长/h | 预报方法 | MAX/ ns |
MEAN/ ns |
RMS/ ns |
| 24 | GM(1, 1) | 8.08 | 3.37 | 4.16 |
| GM(1, 1)-LAD | 5.14 | 1.92 | 2.28 | |
| 48 | GM(1, 1) | 13.02 | 6.10 | 7.05 |
| GM(1, 1)-LAD | 5.72 | 2.58 | 2.94 | |
| 72 | GM(1, 1) | 15.59 | 8.37 | 9.45 |
| GM(1, 1)-LAD | 6.00 | 2.93 | 3.24 | |
| 96 | GM(1, 1) | 17.78 | 10.12 | 11.25 |
| GM(1, 1)-LAD | 6.00 | 2.80 | 3.09 |
| 步长/d | 预报方法 | MAX/ ns |
MEAN/ ns |
RMS/ ns |
| 7 | GM(1, 1) | 26.68 | 14.30 | 15.72 |
| GM(1, 1)-LAD | 6.00 | 2.13 | 2.56 | |
| 14 | GM(1, 1) | 56.88 | 23.49 | 26.28 |
| GM(1, 1)-LAD | 15.69 | 4.63 | 6.00 | |
| 21 | GM(1, 1) | 92.62 | 41.17 | 48.02 |
| GM(1, 1)-LAD | 13.52 | 4.62 | 5.53 | |
| 28 | GM(1, 1) | 95.01 | 51.54 | 58.70 |
| GM(1, 1)-LAD | 34.38 | 7.60 | 10.75 |
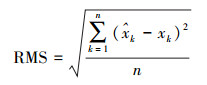 (14)
(14) 式中,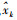
结合图 2—图 4和表 1—表 3可知:在卫星钟差波动较大的情况下,使用传统灰色模型对未来10、12、14、16 h的短期预报的均方根分别为1.64、1.57、1.76、2.15 ns,而基于最小一乘法改进的灰色模型预报的均方根分别为1.56、1.48、1.41、1.42 ns, 相比于传统灰色模型的预报精度分别提高了4.90%、5.70%、19.89%、33.95%;使用传统灰色模型对未来24、48、72、96 h的中长期预报的均方根分别为4.16、7.05、9.45、11.25 ns,而基于最小一乘法改进的灰色模型预报的均方根分别为2.28、2.94、3.24、3.09 ns, 相比于传统灰色模型的预报精度分别提高了45.19%、58.30%、65.71%、72.53%;使用传统灰色模型对未来7、14、21、28 d的长期预报的均方根分别为15.72、26.28、48.02、58.78 ns,而基于最小一乘法改进的灰色模型预报的均方根分别为2.56、6.00、5.53、10.75 ns, 相比于传统灰色模型的预报精度分别提高了83.72%、77.17%、88.48%、81.69%。
从以上预报试验的结果可以看出:在卫星钟差波动较大的情况下,本文改进的方法较传统灰色模型的预报效果有显著改善,并且可以对GPS卫星钟差进行高精度的短期、中长期和长期预报,尤其是对7、14、21、28 d长期预报的精度改善比较大。
4 结语最小二乘法具有良好的解析性并且容易求解,使得该方法在灰色预报模型中成为普遍使用的模型参数估计的方法。但是,由于最小二乘法容易陷入局部最小和稳健性较差的缺陷,使得在卫星钟差波动较大的情况下,预报卫星钟差时不能较好地拟合。本文提出的基于最小一乘法的灰色预报模型,克服了传统灰色预报模型的不足。经理论和预报试验分析,结果也表明了该改进方法的优越性和可行性,从而验证了基于最小一乘法的灰色预报模型算法思路的有效性,为卫星钟差预报研究在实际应用中提供了一定的参考与借鉴。
| [1] |
于烨, 张慧君, 李孝辉. 顾及钟差随机项的GPS卫星钟差预报[J]. 测绘通报, 2018(6): 1-6. |
| [2] |
HUANG G W, ZHANG Q, XU G C. Real-time clock offset prediction with an improved model[J]. GPS Solutions, 2014, 18(1): 95-104. DOI:10.1007/s10291-013-0313-0 |
| [3] |
于烨, 张慧君, 李孝辉. 组合模型在卫星钟差中长期预报中的应用和比较[J]. 电子测量技术, 2017, 40(11): 7-11. |
| [4] |
HUANG G W, ZHANG Q. Real-time estimation of satellite clock offset using adaptively robust Kalman filter with classified adaptive factors[J]. GPS Solutions, 2012, 16(4): 531-539. DOI:10.1007/s10291-012-0254-z |
| [5] |
于烨, 张慧君, 李孝辉. 基于一阶差分修正指数曲线法的GPS卫星钟差预报[J]. 探测与控制学报, 2018, 40(4): 94-98. |
| [6] |
LI M, QU L, ZHAO Q, et al. Precise point positioning with the BeiDou Navigation Satellite System[J]. Sensors, 2014, 14(1): 927-943. |
| [7] |
于烨, 张慧君, 李孝辉, 等. 基于GM(1, 1)和MECM组合模型的GPS卫星钟差中短期预报[J]. 天文学报, 2018, 59(3): 19-30. |
| [8] |
李晓宇, 杨洋, 胡晓粉, 等. 基于改进灰色ARMA模型的卫星钟差短期预报研究[J]. 大地测量与地球动力学, 2013, 33(1): 59-63. |
| [9] |
LIANG Y, REN C, YANG X, et al. A grey model based on first differences in the application of satellite clock bias prediction[J]. Chinese Astronomy and Astrophysics, 2016, 40(1): 79-93. |
| [10] |
YU Y, ZHANG H, LI X. Three kinds of algorithm and its performance analysis in the prediction of satellite clocks bias[C]//Proceedings of the 13th IEEE International Conference on Electronic Measurement and Instruments.[S.l.]: IEEE, 2017: 536-543.
|
| [11] |
梁月吉, 任超, 杨秀发, 等. 结合双树复小波和广义回归神经网络的钟差预报方法研究[J]. 测绘通报, 2016(1): 6-10. |
| [12] |
路晓峰, 杨志强, 贾小林, 等. 灰色系统理论的优化方法及其在卫星钟差预报中的应用[J]. 武汉大学学报(信息科学版), 2008, 33(5): 492-495. |
| [13] |
于烨.存在钟跳情况下的卫星钟差预报[C]//中国天文学会2017年学术年会摘要集.乌鲁木齐: 中国天文学会, 2017: 52-52. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGTW201708001110.htm
|
| [14] |
崔先强, 焦文海. 灰色模型在卫星钟差预报中的应用[J]. 武汉大学学报(信息科学版), 2005, 30(5): 447-450. |
| [15] |
于烨, 张慧君, 李孝辉, 等. 基于Vondrak滤波1阶差分的灰色模型的卫星钟差预报方法[J]. 天文学报, 2018, 59(2): 75-84. |
| [16] |
刘明. 最小一乘法与最小二乘法:基于例证的比较[J]. 统计与决策, 2012(20): 12-15. |
| [17] |
顾乐民. 曲线拟合的最小一乘法[J]. 同济大学学报(自然科学版), 2011, 39(9): 1377-1382. DOI:10.3969/j.issn.0253-374x.2011.09.023 |
| [18] |
谢开贵, 宋乾坤, 周家启. 最小一乘线性回归模型研究[J]. 系统仿真学报, 2002, 14(2): 189-192. DOI:10.3969/j.issn.1004-731X.2002.02.018 |



