GNSS伪距观测量受多路径效应及测量噪声影响明显,其在高精度场景的应用受到限制。相较于伪距,载波相位观测量具有更小的观测噪声,受多路径效应的影响也更小,但需要解决整周模糊度求解及固定问题[1-4],否则在很多实时场景下会导致其应用受限。载波相位平滑伪距滤波是一种有效的GNSS数据处理技术,在很多高精度实时定位场合得到了广泛的应用[5]。其本质上是将高精度的载波相位观测量与低精度的伪距观测量进行融合,一方面削弱了伪距噪声及多路径效应的影响;另一方面避免了载波相位整周模糊度求解问题,使得GNSS观测数据得到了充分利用。与此同时,采用伪距双差、多传感器辅助等方法也能提高伪距观测值的精度[6]。
一般的,按待估参数的类型可将载波相位平滑伪距滤波分为距离域和位置域两大类[7-8]。距离域载波相位平滑伪距是将卫星至接收机天线的距离(考虑接收机钟差及其他误差项,实际上是一种“伪距”)视为待估参数,接收机的最终位置参数可利用平滑后的伪距进一步估计,因此距离域滤波是一种分步最优的估计方法;而位置域载波相位平滑伪距直接估计接收机的位置参数,是一种整体最优的估计方法。最早提出并应用最广的距离域载波相位平滑伪距算法是Hatch滤波。文献[9]提出CCCF(carrier-connected-code filter)位置域载波相位平滑伪距滤波,不同于Hatch滤波的算术平均算法[10],CCCF利用递归最小二乘理论将伪距与相位时间差分观测量进行有效的组合。文献[11]提出了CACF(carrier-adjusted-code filter)位置域滤波,不同于文献[9]利用相位时间差分去除模糊度参数,CACF直接将整周模糊度视为待估参数,其浮点解在历元间传递以实现平滑效果。在递归最小二乘理论框架下,位置域相位平滑伪距滤波要优于距离域,不论是精度层面还是对可见星集合变化不敏感层面[7-9, 12]。
不难发现,载波相位时间差分观测量的观测噪声是时间(或历元间)相关的,换言之,这是一种有色噪声。对于有色噪声一般采用自回归(auto-regressive,AR)模型或Markov模型来表示,但该模型在这里将失效:载波相位时间差分观测量的有色噪声本质上是一种有限冲击响应(finite impulse response, FIR)过程,而AR模型则是一个无限冲激响应(infinite impulse response, IIR)过程,由数字信号处理理论可知,FIR过程无法由有限阶IIR过程严格表示(实际上反之亦然)。尽管有文献曾考虑了这种特殊的有色噪声的影响[7-8],但同时也有一些文献在建立随机模型时并没有对其进行正确描述甚至未被提及,因而在算法推导中也没有进行充分考虑。理论上,该有色噪声是否被充分考虑将会影响(至少在一定程度上)载波相位平滑伪距的效果,进而影响最终的定位精度。基于此,首先,将引入一种特定有色观测噪声条件下的递归最小二乘方法,采用符合实际的随机模型,即正确反映载波相位差分观测量的有色噪声特性,在此模型下采用严格的递归最小二乘方法,得出顾及有色噪声的距离域和位置域相位平滑伪距滤波,并分析忽略有色噪声特性对平滑效果的影响以及距离域与位置域平滑滤波的精度差异;其次,本文将特定有色噪声条件下的递归最小二乘方法推广到双频情形,一方面当前很多接收机可以提供双频观测,另一方面考虑GNSS的发展趋势,双频观测在民用领域也将逐渐普及,因而这种推广将具有显著意义;最后,采用一组实测的GPS数据验证本文算法的有效性。
1 载波相位平滑伪距算法 1.1 观测模型GNSS系统的多频伪距和载波相位的观测方程为
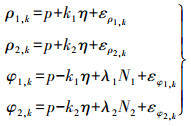 (1)
(1) 式中,ρ、φ分别表示伪距和载波相位观测量;p表示卫星至接收机的无色散距离(伪距),包含卫星钟差、接收机钟差、对流层误差及相对论效应的影响;N表示整周模糊度;η表示L1频率上电离层误差的影响;ε表示观测噪声;ki=f12/fi2, i=1、2;下标数字表示频率;k表示观测历元。
1.2 传统双频距离域无电离层Hatch滤波电离层对伪距和相位观测量影响的差异,导致在单频Hatch滤波算法中通常需设定固定的平滑时间因子来防止滤波发散[13]。一般的,单频用户可利用模型对电离层误差进行修正[14],双频用户则可利用观测量的无电离组合来消除电离层的影响[15]。在双频载波相位平滑伪距算法中可使用无电离组合的伪距和载波相位观测量来消除电离层差异对滤波的影响,双频Hatch滤波算法可总结为
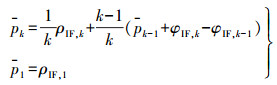 (2)
(2) 式中,p表示平滑后的伪距;ρIF、φIF分别表示伪距和相位的无电离组合。从式(2)可知,上个历元相位的观测噪声与平滑伪距是相关的,即观测量之间存在有色噪声,该有色噪声将在后续算法中充分考虑。需要指出的是,双频Hatch滤波虽然可以完全消除低阶电离层的影响,但是由于伪距的无电离组合会引进两个载波频率上的伪距噪声,因此双频无电离层Hatch的代价是放大了伪距噪声影响[10, 16]。
1.3 顾及有色噪声距离域双频相位平滑伪距滤波不同于双频无电离层Hatch滤波利用双频观测组合消除电离层的影响,新的距离域双频平滑伪距滤波在递归最小二乘理论框架下,将电离层误差和无色散距离(伪距)同时视为待估计量,利用多频观测的伪距及载波相位差分观测量对其进行直接估计,载波相位差分观测量的有色噪声也得到充分的考虑。根据式(1),顾及有色噪声影响的双频距离域相位平滑伪距滤波可总结为
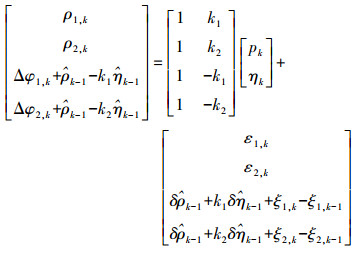 (3)
(3) 式(3)可以简写为
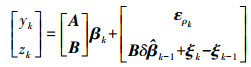 (4)
(4) 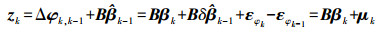 (5)
(5) 式中,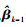
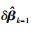
从式(5)可知,当前历元的参数估计与上个历元的观测量相关,根据误差传播定律有如下的方差关系
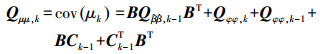 (6)
(6) 式中,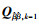
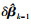
结合式(4)—式(6),递归最小二乘理论框架下有
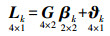 (7)
(7) 其中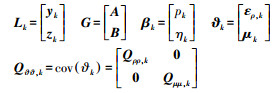
上式的最小二乘解为
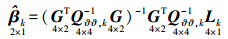 (8)
(8) 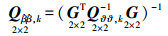 (9)
(9) 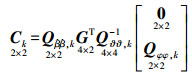 (10)
(10) 对于初始历元,由于只使用了伪距观测量,而没有涉及载波相位时间差分量,于是有Ck=0=0。另外需指出的是,由于距离域滤波结构的特点,每颗卫星的数据是分开单独进行滤波,得到每颗卫星的平滑伪距和对应的电离层估计。
1.4 顾及有色噪声位置域载波相位平滑伪距滤波式(8)给出了无色散距离(伪距)和电离层误差的最优估计,但在大多数应用场景下,直接感兴趣的是位置参数。尽管距离域滤波可以利用平滑后的伪距来进行位置参数的估计,不同于距离域滤波的分步最优估计,位置域滤波采用一步整体最优估计方法直接估计最终的位置参数。由于采用的是多通道数据同时处理,不同于距离域滤波的单通道处理策略,可以将每颗卫星对应的电离层误差进行单独估计,在位置域滤波考虑待估参数的数量及计算量,对电离层误差不进行估计,而是采用电离层模型来减小其影响或采用短基线差分模式。因此,位置域滤波的待估参数为三维坐标及接收机钟差,即θk=[xk yk zk δtk]T,此时假设电离层延迟、对流层延迟、卫星钟差均已经过模型改正,将式(1)的伪距和相位观测方程线性化有
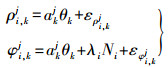 (11)
(11) 式中,i表示载波频率;j表示第j颗卫星;k表示观测历元;akj表示线性化后的系数。
在递归最小二乘理论框架下将式(11)改写成向量形式,即
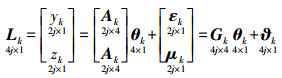 (12)
(12) 需要指出的是,式(12)中的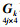
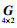
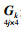
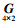
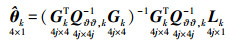 (13)
(13) 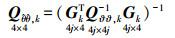 (14)
(14) 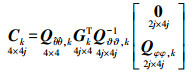 (15)
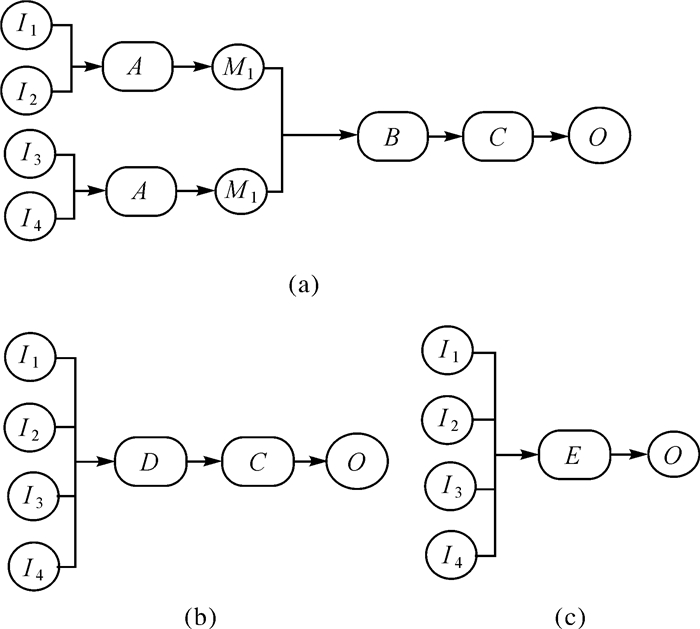
(15) 图 1为不同载波相位平滑伪距方法的流程。图 1(a)表示传统双频无电离Hatch滤波;图 1(b)表示双频距离域滤波;图 1(c)表示双频位置域滤波;I1~I4表示GNSS原始观测量;A表示无电离组合;M1表示中间变量;B表示Hatch滤波;C表示单点定位;O表示输出量;D表示距离域滤波;E表示位置域滤波。由图可知,双频无电离Hatch滤波与距离域滤波是一种分步最优的平滑方法,而位置域滤波是一步整体最优平滑。理论上,依据误差传播定律,3种平滑方法的精度从高到低依次为图 1(c)、(b)、(a)。
|
| 图 1 不同载波相位平滑伪距方法流程 |
综上,载波相位平滑伪距的实质是伪距与相位观测量的融合,不同于传统Hatch方法的低通滤波原则,本文则是利用递归最小二乘理论来实现GNSS观测数据的融合,从而达到平滑伪距的目的,并在最小二乘理论框架下充分考虑了有色噪声的影响。
2 实例分析为验证平滑伪距算法的应用效果及其有效性,本文进行了GPS静态数据的采集,其点位坐标精确已知,GPS数据采样间隔为1 s,卫星高度截止角为5°。采用3种平滑算法分别对伪距进行平滑,再利用单点定位算法进行接收机位置的解算。在单点定位算法中,卫星钟差、对流层误差均利用模型进行修正,且在位置域滤波中电离层误差利用Klobuchar模型进行改正。本文从以下几个方面进行了试验:
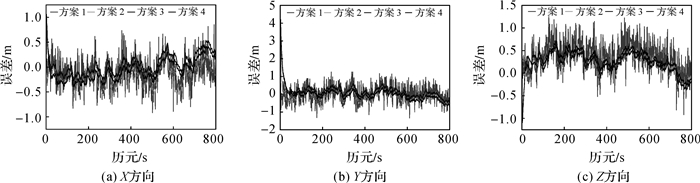
首先,为了对比算法的平滑效果,采用4种方案进行数据处理,即原始未平滑数据(方案1)、双频无电离Hatch滤波(方案2)、距离域滤波(方案3)、位置域滤波(方案4)。图 2为4种方案在X、Y、Z 3个方向的误差序列图。从误差序列图可以看出,采用了平滑算法的方案2、方案3、方案4的结果明显优于原始数据计算结果,说明载波相位平滑伪距算法能够有效减小伪距观测值的误差,提高伪距观测量的精度;方案3的结果优于方案2,说明最小二乘理论框架下的平滑算法要优于一般的数字低通滤波方法;方案4优于方案3,说明一步整体最优的位置域估计要优于分步最优的估计方法。
|
| 图 2 方向误差 |
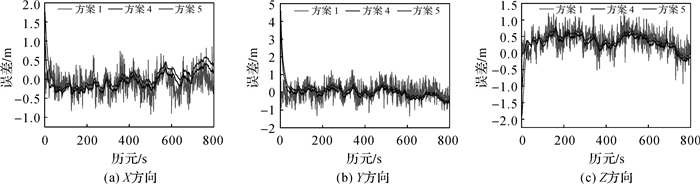
为了验证有色噪声对平滑算法的影响,在方案4的基础上,采用两种方案进行验证,即未考虑有色噪声的位置域滤波(方案5)及考虑有色噪声影响的位置域滤波(方案4)。图 3给出了两种方案在X、Y、Z 3个方向的误差序列图。由图可知,方案4的平滑效果要优于方案5,说明在相位平滑伪距算法中,载波相位时间差分量之间存在的相关性对平滑性能有一定的影响,因此在一些高精度的应用场景下这种有色噪声需要给予充分的考虑,才能不失算法的严谨性。
|
| 图 3 方向误差 |
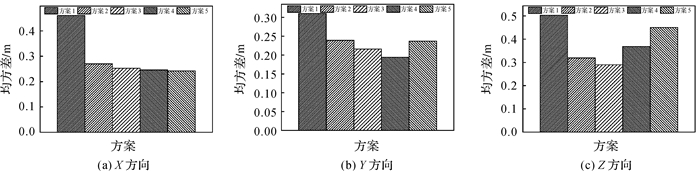
为更加精确地比较4种方案的平滑效果,对X、Y、Z 3个方向误差的均方差(RMS)进行统计(见表 1),并通过直方图的方式进行了对比(如图 4所示)。可以看出,4种方案的误差均方差大小依次为方案1、方案2、方案3、方案4,方案2、3、4在3个方向的均方差误差小于方案1。与方案1比较,方案2在X、Y、Z 3个方向上的误差分别降低了23%、41%、37%;与方案2相比,方案3在3个方向上的误差分别降低了10%、6%、6%;与方案3相比,方案4在X、Y方向上的误差分别降低了10%、3%。从图 4和表 1中方案4与方案5的数据比较可得有色噪声对相位平滑伪距算法的影响,在本试验中,若考虑了载波相位时间差分量的有色噪声,则平滑精度在X、Z方向上将能够提高18%左右。
|
| 图 4 方向误差均方差统计 |
| m | |||
| 方法 | 均方差 | ||
| X | Y | Z | |
| 方案1 | 0.310 | 0.461 | 0.503 |
| 方案2 | 0.239 | 0.270 | 0.319 |
| 方案3 | 0.216 | 0.253 | 0.290 |
| 方案4 | 0.194 | 0.246 | 0.369 |
| 方案5 | 0.237 | 0.242 | 0.450 |
本文在传统的单频载波相位平滑伪距的基础上,提出了在最小二乘理论框架下利用双频载波相位时间差分量进行距离域和位置域的伪距平滑算法,并充分考虑了载波相位时间差分量的有色噪声影响,建立了误差正确的随机模型。试验结果表明,相位平滑伪距算法能够有效减小伪距观测值的误差,提高伪距观测量的精度;距离域滤波和位置域滤波定位结果的稳定性要优于传统的伪距平滑算法;同时,载波相位时间差分量的有色噪声对平滑效果存在一定影响,若忽略这种有色噪声,滤波精度在一定程度上会受到损失。
| [1] |
TEUNISSEN P J G. The least-squares ambiguity decorrel-ation adjustment:a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. DOI:10.1007/BF00863419 |
| [2] |
TEUNISSEN P J G. Integer aperture GNSS ambiguity resolution[J]. Artificial Satellites, 2003, 38(3): 79-88. |
| [3] |
TEUNISSEN P J G, VERHAGEN S. The GNSS ambiguity ratio-test revisited:a better way of using it[J]. Survey Review, 2009, 41(312): 138-151. DOI:10.1179/003962609X390058 |
| [4] |
VERHAGEN S, TEUNISSEN P J G. The ratio test for future GNSS ambiguity resolution[J]. GPS Solutions, 2013, 17(4): 535-548. DOI:10.1007/s10291-012-0299-z |
| [5] |
郑南山, 李增科. 多普勒平滑伪距在GPS与INS紧耦合导航中的应用[J]. 武汉大学学报(信息科学版), 2014, 39(10): 1159-1162. |
| [6] |
孙红星, 闫利, 姜卫平. 高精度GPS差分载波相位多普勒/INS新型全组合解算机载TLS外方位元素[J]. 武汉大学学报(信息科学版), 2004, 29(7): 642-645. |
| [7] |
LEE H K, RIZOS C, JEE G I. Design of kinematic DGNSS filters with consistent error covariance information[J]. IEE Proceedings-Radar, Sonar and Navigation, 2004, 151(6): 382-388. DOI:10.1049/ip-rsn:20041026 |
| [8] |
LEE H K, RIZOS C, JEE G I. Position domain filtering and range domain filtering for carrier-smoothed-code DGNSS:an analytical comparison[J]. IEE Proceedings-Radar, Sonar and Navigation, 2005, 152(4): 271-276. DOI:10.1049/ip-rsn:20059008 |
| [9] |
BISNATH S B, LANGLEY R B. Precise rrbit determina-tion of low earth orbiters with GPS point positioning[J]. ION NTM, 2001, 122(1): 725-733. |
| [10] |
CHANG Z Q. Comparison between CNMC and hatch filter and its precision analysis for BDS precise relative positioning[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2015, 45(7): 124-130. |
| [11] |
TEUNISSEN P J G. The GPS phase-adjusted pseudo-range[J]. Proceedings of the 2nd International Workshop on High Precision Navigation, 1991, 100(2): 543-556. |
| [12] |
BISNATH S B, LANGLEY R B. High-precision, kinematic positioning with a single GPS receiver[J]. Navigation, 2002, 49(3): 161-169. DOI:10.1002/navi.2002.49.issue-3 |
| [13] |
HWANG P Y, MCGRAW G A, BADER J R. Enhanced differential GPS carrier-smoothed code processing using dual-frequency measurements[J]. Navigation, 1999, 46(2): 127-137. DOI:10.1002/navi.1999.46.issue-2 |
| [14] |
KLOBUCHAR J A. Ionospheric time-delay algorithm for single-frequency GPS users[J]. IEEE Transactions on Aerospace & Electronic Systems, 1987, AES-23(3): 325-331. |
| [15] |
LI Bofeng. Undifferenced cycle slip estimation of triple-frequency BeiDou signals with ionosphere prediction[J]. Marine Geodesy, 2016, 39(5): 348-365. DOI:10.1080/01490419.2016.1207729 |
| [16] |
MCGRAW G. Generalized divergence-free carrier smoothing with applications to dual frequency differential GPS[J]. Navigation-Journal of the Institute of Navigation, 2006, 56(2): 115-122. |
| [17] |
CHANG Guobing. On Kalman filter for linear system with colored measurement noise[J]. Journal of Geodesy, 2014, 88(12): 1163-1170. DOI:10.1007/s00190-014-0751-7 |


