2. 中国矿业大学环境与 测绘学院, 江苏 徐州 221116;
3. 武汉大学遥感信息工程学院, 湖北 武汉 430079
2. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China;
3. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
土壤全钾含量是植物生长的主要营养元素,同时也是土壤中影响农作物产量的三要素之一[1]。研究土壤钾含量的空间分布特征,不仅对均衡和扩展土壤有效养分库具有重要意义,还能为土地资源可持续利用和地区农业的健康发展提供理论依据[2]。近几年来,国外文献[3-4]对土壤空间变异规律进行了深层次的研究;国内文献[5]对土壤重金属、土壤有机质的空间变异进行研究,取得了大量的研究成果。青海湖流域作为典型的复杂地貌类型区,研究土壤全钾含量对改善地区施肥效果、提高土壤利用效率具有一定的现实意义[6]。
土壤属性的连续变化是土壤资源科学管理和使用的前提,土壤各类属性的空间插值是用来评估土壤性质连续变化的主要方法[7],同时也是“数字土壤”和“土壤计量学”的一个重要研究工具。空间插值精度取决于很多因素,一部分研究成果表明Kriging的模拟效果优于反距离加权法(inverse distance weighting method, IDW)和Spline, 而另一部分研究成果持相反观点[8]。如文献[9]通过比较3种插值方法评价土壤全氮含量的插值误差,得出径向基函数法插值模型优于普通克里金插值法(ordinary kriging, OK)和IDW。修思玉等通过3种插值方法评价黑龙江省2010年32格气象站点的年降雨量,采用平均误差、平均绝对误差、平均相对误差等指标进行优度检验,得出Spline法最优、IDW得到的降雨量的最大值与最小值与原始降雨量数据相差最大。文献[10]对比了土壤Cd污染插值模型,得出不同的插值方法对极大值都存在不同程度的平滑。综合以上研究发现,目前对空间属性曲面建模的研究主要集中在单一全局插值模型。因此研究基于空间属性的自适应曲面建模具有重要的意义。
此外,一系列研究论证了利用地学环境变量为补充信息能够有效提高插值精度。文献[11]以高程、坡度、土地利用等辅助变量预测土壤精度。文献[12]采用土壤电导率变量对不同尺度的土壤盐分开展了空间变异特征的随机模拟。文献[13]采用NDVI、高程和距河流距离为辅助变量研究黄河三角洲地区的盐渍化,指出结合地学环境变量的插值模拟效果更好。但是,结合地学环境变量的插值模型也存在一些不足,如很多研究使用单一、同类的地学环境变量解决不同地区的预测问题,然而不同地区受到不同因素影响,其考虑的环境变量是不同的。各个插值方法的适应性不同,不存在绝对最优的空间插值模型,若能根据不同的插值模型自身的适应性,分区进行多模型集成,理论上可以提高模拟精度。
1 研究区概况与采样方法 1.1 青海湖自然概况研究区(36°38′N-37°29′N, 99°52′E-100°50′E)地处青海湖流域东南部。由于地壳运动形成了复杂多样的地貌类型,地貌以冲击洪积扇平原为主,流域周围大小河流40余条,属于内陆封闭水系,是许多野生动物的栖息繁殖区域。青海湖流域属高原半干旱的温带大陆性气候,位于冻土地带,干旱少雨,多风,太阳辐射强,温差变化较大。研究区主要包括共和、刚察和海晏3个地区,除去青海湖,总面积约为2100 km2, 海拔高度为3043~4516 m,有大量不同的土壤、植被、地貌类型,属于典型的复杂地貌类型区。
1.2 样品采集研究通过空间分层组合的方式[14]进行土壤采样。在土壤采样的同时记录了采样点的经纬度、海拔、土地利用类型、土壤类型、植被类型及地质类型等与土壤属性密切相关的地学环境信息,每个样点在0~15 cm、15~30 cm依次采样两次。笔者于2013年9月,在青海省环境检测中心人员提供协助下,收集了青海湖典型地区土壤表层(0~30 cm)样点数据110个。采样结束后在实验室对样品进行风干、研磨、过2 mm筛等流程后,取两次土壤中全钾元素的含量平均值作为记录样本值。
2 研究方法 2.1 地学环境要素筛选已有研究表明,利用地学环境要素作为辅助变量能够有效提高土壤全钾含量插值精度和制图效果。土壤全钾空间变异性驱动因子主要包括:土地利用类型、土壤类型、植被类型、地质类型、坡度、施肥等[15-16]。根据已有的研究结论,结合本次主要针对自然景观类型区研究,排除施肥和土地管理措施2个驱动因子,选取土地利用类型、土壤类型、植被类型、地质类型4个地学环境要素作为辅助变量。其中土地利用类型有灌丛、耕地和草原等6种;土壤类型有栗钙土、流动和风沙土等5种;植被类型有水柏枝草场型、紫花针茅杂草草场型等30种;地质类型有沙丘、沙山和河谷平原等13种。使用SPSS计算辅助变量的土壤全钾含量统计特征。为了进一步筛选对土壤全钾空间分布具有显著影响的地学要素,利用SPSS软件对土壤全钾含量与上述4个地学要素进行方差分析,选取具有显著特征的地学要素作为辅助环境变量。表 1的方差结果分析表明:在本文研究区域内,植被类型的景观破碎度太高,很多区域内只有1个采样点,一些亚类型的草地只有1~2个采样点,模拟效果不理想,因此将植被类型排除在外。
| 地学要素 | 方差来源 | 自由度 | 方差之和 | 平均方差 | F值 | P值 |
| 土地利用类型 | 组间方差 | 106 | 4.631 | 0.116 0.044 |
2.645 | 0.038* |
| 组内方差 | 4 | 0.462 | ||||
| 总方差 | 110 | 5.093 | ||||
| 土壤类型 | 组间方差 | 106 | 4.371 | 0.181 0.041 |
4.378 | 0.003** |
| 组内方差 | 4 | 0.722 | ||||
| 总方差 | 110 | 5.093 | ||||
| 植被类型 | 组间方差 | 94 | 4.159 | 0.058 0.044 |
1.319 | 0.202 |
| 组内方差 | 16 | 0.934 | ||||
| 总方差 | 110 | 5.093 | ||||
| 地质类型 | 组间方差 | 101 | 4.060 | 0.115 0.04 |
2.856 | 0.005** |
| 组内方差 | 9 | 1.033 | ||||
| 总方差 | 110 | 5.093 | ||||
| 注:*0.05显著水平;**0.01显著水平。 | ||||||
本文中对土壤钾含量进行空间插值的4种方法均基于ArcGIS 10.2平台实现。传统的插值方法有OK、IDW、回归克里金(regression Kriging, RK)、贝叶斯克里金(Bayesian Kriging, BK)。OK在满足二阶平稳假设和内蕴条件的基础上,根据区域化变量的原始数据和变异函数(或协方差)的特点,确定待估点周围已知点参数对待估点的加权值大小,再对待估点做出最优估计的方法,其优点是顾及各样本点的空间相关性,在得到模拟结果的同时,得出估算精度的方差;IDW使用一组采样点的线性权重组合来确定输出的栅格值,权重与插值点和样本点之间的距离成反比,是一种加权移动平均的方法;RK综合考虑了影响钾空间变异的多种环境因子,但由于研究区环境要素分布比较破碎,导致没有足够多的采样点来估计相对准确的半方差函数。对全钾含量进行半变异分析,得到插值时的各参数值和拟合模型,其中块金值较小,表明自身随机性误差引起的变异性不大;S/N+S比值接近于1,N/S比值小于30%,表明全钾含量具有较强的空间相关性,拟合的最优模型为指数模型[15]。
2.2.2 融合地学环境要素的自适应曲面建模方法 2.2.2.1 融合地学环境要素的基插值模型根据变异和空间相关理论,任何变量的空间变化都可以用下述两个主要成分之和来表示:与局部变化有关的残差成分、与趋势有关的结构成分。相应的土壤全钾含量的空间分布模式可以表示为
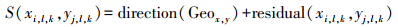 (1)
(1) 式中, S(xi, l, k, yj, l, k)为第l种地学要素的第k种类型的土壤全钾采样点模拟值,其中(xi, yj)为采样点坐标,i和j分别表示坐标的行和列;direction(Geox, y)是描述(xi, yj)处第l种地学要素的第k种类型S的趋势值,其中Geo(x, y)是描述(xi, yj)处与土壤全钾密切相关的地学环境信息;residual(xi, l, k, yj, l, k)是描述(xi, yj)处S的第l种地学要素的第k种类型中第i行、第j列栅格点土壤全钾的残差值。基于均值模型得到趋势函数,拟合描述结构成分的趋势面,实现趋势分离;并根据土壤厚度采样点的空间特征,比较选择最佳的空间相关插值算法对残差进一步处理。基于以上理论知识,具体试验方案如图 1所示。
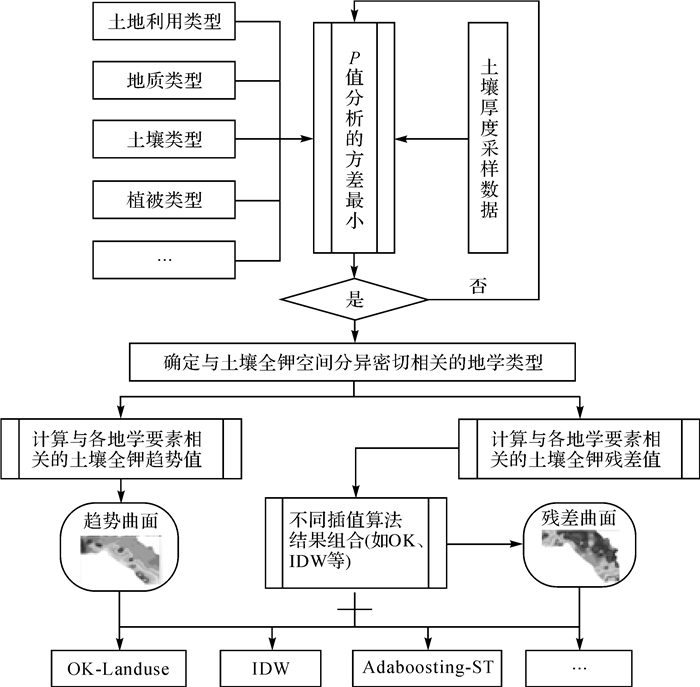
|
| 图 1 地学类型筛选与基插值曲面建模流程 |
根据上述建立的基插值模型Modeli对整个研究区进行模拟生成一系列土壤全钾插值曲面,使用采样点土壤全钾实测值减去预测值得到模拟误差,以扫面线算法(算法步骤如图 2所示)为集成学习的分类学习器,对插值曲面进行扫描,选择分类正确率较高且差异较大的扫描线进行集成,对各个插值曲面进行多种类的自适应分区,得到各个插值模型适用的空间范围。
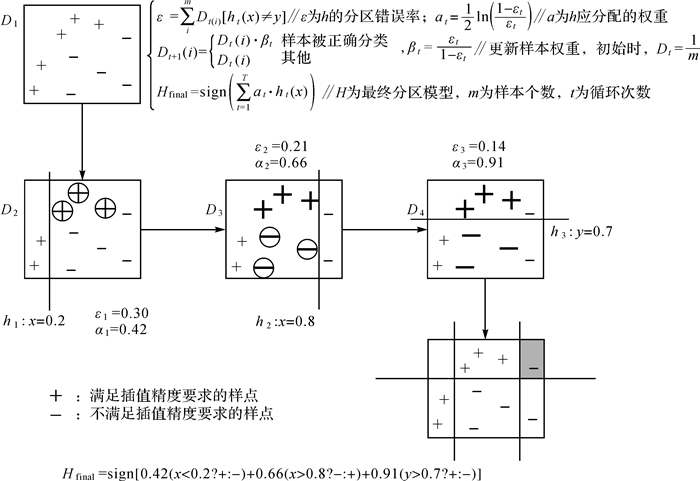
|
| 图 2 扫描线算法的分区过程 |
“+”和“-”分别表示满足插值精度要求的样点和不满足插值精度要求的样点。在这个过程中,使用水平和垂直的扫描线作为分类器,对土壤全钾插值曲面进行分区。
(1) 根据对插值曲面分区的正确率,得到一个新的样本分布(即样本中每个样本点的权重分布)D2、一个子分类器h1。其中画圈的样本表示被分错的,比较大的“+”表示对该样本作了加权。
(2) 根据分区的正确率,得到一个新的样本分布D3、一个子分类器h2。弱分类器h2中有3个“-”符号分类错误,得到分区错误率ε2=0.21,h2应分配的权重α2=0.66。
(3) 得到一个子分类器h3。弱分类器h3中有2个“+”符号和一个“-”符号分类错误,得到分区错误率ε3=0.14,h3应分配的权重α3=0.91。
(4) 整合所有子分类器,得到最终的Hfinal。经过以上三步即可抽取所有满足精度阈值的分区,每个区域属于哪个类别,由该区域所在分类器的权值综合决定。经过集成和NO Data区域的填充,得到土壤属性自适应曲面建模方法(adaptive surface modeling for soil properties, ASM-SP)模拟的空间分布图。
2.3 插值结果精度检验独立验证模型存在检验精度不够的问题,使用交叉验证能够更优评价插值方法的质量[17-19]。在交叉验证中,针对110个监测点中的每一个点位数据,假设其数据未知,基于其余109个点位的数据,使用不同插值方法计算出模拟值,再结合观测值求算误差。
交叉验证的评定指标有平均估计误差百分比(PAEE)、相对均方差(RMSE)、均方根预测误差(RMSPE)及残差分析等。本文采用最大误差(max error)、最小误差(min error)、平均误差(ME)、均方根误差(RMSE)。
3 模拟结果与分析 3.1 土壤全钾含量的统计特征从研究区110个表层土壤钾含量的统计结果分析(如图 3所示)可以看出,土壤钾含量的值介于1.406 5%~2.346 4%之间,平均值为1.958 8%,K-S检验结果表明钾含量总体上服从正态分布。土壤钾含量的变异系数为10.99%,表明研究区土壤钾含量的空间变异性处于中等水平[15]。
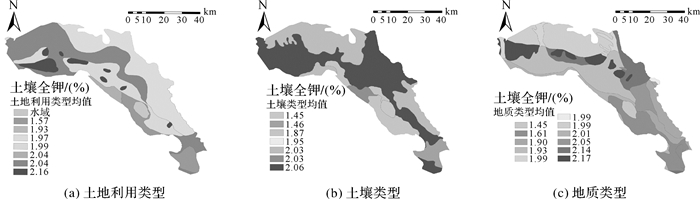
|
| 图 3 不同辅助变量的趋势曲面 |
ASM-SP由3个步骤组成:①建立一系列基插值模型,即OK-Landuse,OK-Soil,OK-Geology;②基插值曲面的自适应分割;③基插值优化组合。自适应分区方法详见2.2节。ASM-SP构建过程如下:
3.2.1 基插值模型建立(1) 计算每种地学要素的土壤全钾均值并得到趋势曲面direction(Geox, y),根据土壤全钾实测值,结合辅助变量,得到土壤全钾平均值(如图 3所示)。
(2) 用实测值减去土壤全钾含量均值,计算得到土壤全钾的模拟残差。对模拟残差进行OK插值得到残差曲面residual(xi, l, k, yj, l, k)(如图 4所示)。
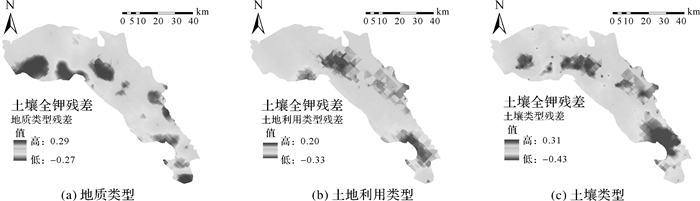
|
| 图 4 不同辅助变量的残差曲面 |
(3) 利用式(1)计算第l种地学要素的第k种类型的土壤全钾采样点模拟值S(xi, l, k, yj, l, k),即将上述的趋势曲面和残差曲面相加。这是基插值曲面的构造过程。
3.2.2 基于线性扫描算法的自适应曲面分割基于第2.2.2节所述的构造误差曲面的方法,获得不同插值模型的误差面(如图 5所示),并确定每个插值模型的适用范围。
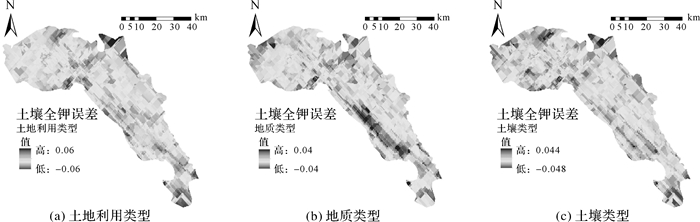
|
| 图 5 基插值模型的误差曲面 |
在栅格单元优化的基础上,选取具有最小误差的栅格单元的插值结果作为最佳栅格单元进行集成。图 6显示了与不同插值模型相对应的最优分区。
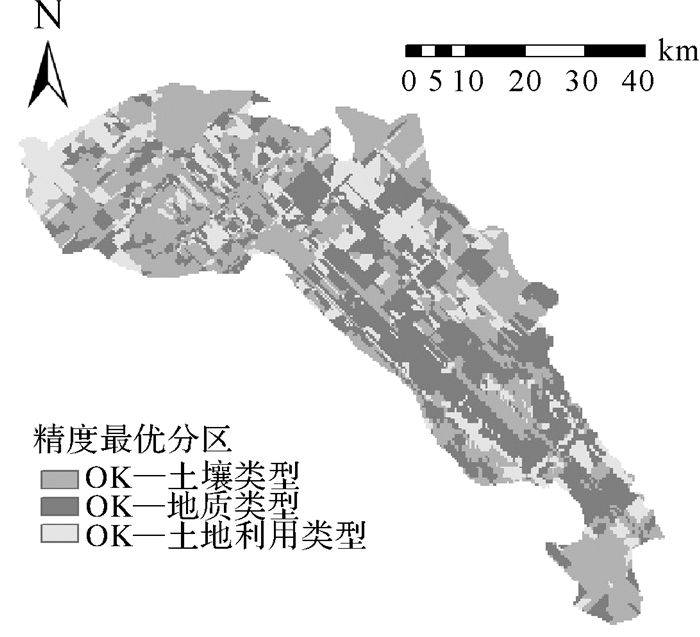
|
| 图 6 ASM-SP模型优化的区域分布 |
为了评价ASM-SP模拟土壤全钾含量空间分布的精度,本文比较了5种插值方法的精度,即RK、BK、IDW、OK+Landuse和ASM-SP。OK、BK结合辅助变量Landuse,与ASM-SP进行对比;RK方法结合Landuse拟合趋势项。逐点交叉验证的误差指标(见表 2), 对于最大误差值来说数值小精度高,对于最小误差值来说数值小精度高。表明ASM-SP预测误差范围最小,预测值的灵敏度和反映极值的情况优于其他4种方法。针对ME和RMSE这几个值而言,ASM-SP分别达到-0.002 1、0.281 1,相对其他结果较优,且精度AC值最优,因此ASM-SP显示出更好的性能,其ME值比传统插值方法(即OK和IDW)的ME值更接近于0。这意味着结合辅助变量的插值更加具有无偏性。并且ASM-SP的精度也充分表明其回归曲线可以更好模拟预测值与真实值的关系。综上所述ASM-SP的插值方法最优。
| 插值方法 | max error | min error | ME | RMSE | AC |
| RK | 5.141 2+E01 | 2.750 8-E02 | 0.007 3 | 0.321 3 | 0.927 3 |
| BK | 5.189 9+E01 | 2.345 5-E02 | -0.005 3 | 0.219 7 | 0.918 7 |
| IDW | 5.549 1+E01 | 3.450 7-E02 | 0.009 2 | 1.056 7 | 0.875 9 |
| OK+Landuse | 5.231 1+E01 | 1.231 9-E02 | 0.008 7 | 0.978 8 | 0.897 7 |
| ASM-SP | 5.123 1+E01 | 2.231 1-E02 | -0.002 1 | 0.281 1 | 0.931 5 |
总的来说,ASM-SP插值方法优于其他方法的主要原因有:①该方法结合了辅助变量,因此更准确地刻画土壤全钾随地学环境要素变化而突出的边界;②使用线性扫描算法将最优区分割出来,并按此方法将各个地学要素得到最优区域整合,在很大程度上提高了插值的精度。
3.4 不同预测方法效果对比本文对比了5种土壤全钾含量的插值效果(如图 7所示)。从图 7中可以看出,RK、BK和OK刻画的变异程度较真实值区间小,插值显示出不同程度的弱“牛眼”效应。IDW插值可以体现出土壤全钾分布的总体格局,但具有较强的“牛眼”效应,且插值精度较低。
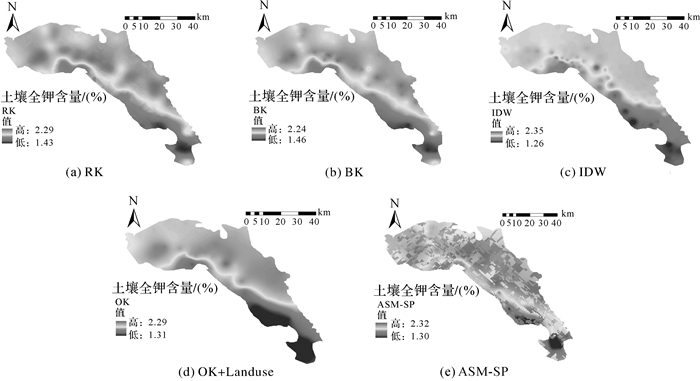
|
| 图 7 不同方法的土壤空间插值图对比 |
ASM-SP能够有效地刻画土壤全钾空间变异格局,生成一个适中的插值范围(1.30~2.32),且能体现土壤全钾空间分异较多的局部变化细节。BK、RK和OK插值得到的土壤全钾值和IDW插值无法描述土壤属性随地学环境变量变化导致的突变边界信息。ASM-SP方法对地形复杂地貌类型区土壤属性的空间插值具有较强的适应性,能更准确地描述研究区土壤属性的空间变异格局。
4 结语利用地学环境变量对插值结果进行修正,能够解决土壤属性空间分异突变的问题,尤其能够解决在丘陵沟壑等复杂地貌区和不同地学要素衔接区产生较大突变的问题。土壤属性的空间分异在较短水平距离内产生较大的变化,导致单一全局插值模型精度有限。因此本文提出了一种融合地学环境要素,将不同插值模型最优区进行自适应建模(ASM-SP)方法。在复杂地貌类型区,ASM-SP能够更准确地刻画土壤属性的空间变异,有效降低模拟误差。此外ASM-SP结合辅助变量,使其模拟结果更符合地学规律,便于物理解释土壤属性的空间变异特征。
对比未使用辅助变量的空间插值模型(IDW、OK),以及利用地形因子辅助插值的RK法的结果显示,ASM-SP刻画土壤全钾含量更加符合研究区土壤属性空间变异规律,地学要素边缘的细节信息表现得更加明显。ME和RMSE等精度评价指标也更小,分别达到-0.002 1和0.281 1,显示出比其他插值模型更高的模拟精度,尤其能准确刻画复杂地貌类型区土壤全钾空间变异随周围地学环境要素变化而突出的边界。ASM-SP是实现复杂地貌类型区土壤全钾含量的高精度模拟的一种新方法,为以后的土壤属性制图研究提供了新思路和有益借鉴。
| [1] |
陈鸽, 汤春纯, 李祖胜, 等. 不同施肥措施对洞庭湖平原区旱地肥力及作物产量的影响[J]. 中国生态农业学报, 2017, 25(5): 689-697. |
| [2] |
董洪芳, 于君宝, 孙志高, 等. 黄河口滨岸潮滩湿地植物-土壤系统有机碳空间分布特征[J]. 环境科学, 2010, 31(6): 1594-1599. |
| [3] |
OBALUM S E, OPPONG J, IGWE C A, et al. Spatial variability of uncultivated soils in derived savanna[J]. International Agrophysics, 2013, 27(1): 57-67. DOI:10.2478/v10247-012-0068-9 |
| [4] |
ROSEMARY F, VITHARANA U W A, INDRARATNE S P, et al. Exploring the spatial variability of soil properties in an Alfisol soil catena[J]. Catena, 2017, 150: 53-61. DOI:10.1016/j.catena.2016.10.017 |
| [5] |
赵明松, 张甘霖, 王德彩, 等. 徐淮黄泛平原土壤有机质空间变异特征及主控因素分析[J]. 土壤学报, 2013, 50(1): 1-11. |
| [6] |
龙军, 张黎明, 沈金泉, 等. 复杂地貌类型区耕地土壤有机质空间插值方法研究[J]. 土壤学报, 2014, 51(6): 1270-1281. |
| [7] |
史文娇, 岳天祥, 石晓丽, 等. 土壤连续属性空间插值方法及其精度的研究进展[J]. 自然资源学报, 2012, 27(1): 163-175. |
| [8] |
马成霞, 丁建丽, 王璐, 等. 绿洲土壤表层含盐量空间变异分析的插值方法研究[J]. 水土保持研究, 2014, 21(4): 317-320. |
| [9] |
赵巧丽, 郑国清, 冯晓, 等. 河南省安阳县三种土壤全氮含量空间插值方法的比较分析[J]. 土壤通报, 2012, 43(5): 1162-1166. |
| [10] |
谢云峰, 陈同斌, 雷梅, 等. 空间插值模型对土壤Cd污染评价结果的影响[J]. 环境科学学报, 2010, 30(4): 847-854. |
| [11] |
KURIAKOSE S L, DEVKOTA S, ROSSITER D G, et al. Prediction of soil depth using environmental variables in an anthropogenic landscape:a case study in the Western Ghats of Kerala, India[J]. Catena, 2009, 79(1): 27-38. DOI:10.1016/j.catena.2009.05.005 |
| [12] |
江贵荣.干旱区不同尺度土壤盐分空间变异特征及不确定性分析[D].北京: 中国地质大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10491-1012446541.htm
|
| [13] |
吴春生, 黄翀, 刘高焕, 等. 黄河三角洲土壤含盐量空间预测方法研究[J]. 资源科学, 2016, 38(4): 704-713. |
| [14] |
杨琳, 朱阿兴, 张淑杰, 等. 土壤制图中多等级代表性采样与分层随机采样的对比研究[J]. 土壤学报, 2015, 52(1): 28-37. |
| [15] |
王胜利, 刘伟, 张连蓬, 等. 地学环境变量支持的土壤全钾含量自适应曲面建模——以青海湖流域典型地区为例[J]. 水土保持研究, 2018, 25(1): 132-138. |
| [16] |
黄文忠.宜宾市土壤钾素的空间变异特征及影响因素研究[D].雅安: 四川农业大学, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1800620
|
| [17] |
徐爱萍, 圣文顺, 舒红. 时空积和模型的数据插值与交叉验证[J]. 武汉大学学报(信息科学版), 2012, 37(7): 766-769. |
| [18] |
李佳, 段平, 吕海洋, 等. 基于改进的逐点交叉验证的RBF形态参数优化方法及其空间插值实验[J]. 地理与地理信息科学, 2016, 32(3): 39-42. DOI:10.3969/j.issn.1672-0504.2016.03.008 |
| [19] |
顾春雷, 杨漾, 朱志春. 几种建立DEM模型插值方法精度的交叉验证[J]. 测绘与空间地理信息, 2011, 34(5): 99-102. DOI:10.3969/j.issn.1672-5867.2011.05.032 |



