2. 中国测绘科学研究院, 北京 100830;
3. 辽宁工程技术大学, 辽宁 阜新 123000
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. School of Geomatics, Liaoning Technical University, Fuxin 123000, China
地球质心(center of mass,CM)是整个地球的质量中心,地表物质变迁引起CM相对于地球参考框架原点的位移称作地心运动[1]。CM是地球参考系的原点,建立地心运动的观测模型用于参考框架原点的改正,将会进一步提高空间大地测量精度。同时地心运动蕴含了丰富的地球物理信息,在研究时变重力场等领域中也发挥着重要作用[2]。故测定分析地心运动成为一项必要的工作。
许多学者利用GPS和SLR等空间大地测量技术在测定地心运动方面作了大量相关研究。目前常用的地心运动反演方法有网平移法[3-4]、动力法[5-8]和一阶形变法[9-10]等。研究均发现了地心运动存在周年和近半年的周期分量。但不同方法求得的振幅存在一定差异,对于其他周期项的估计也不完全相同,信号混淆是造成这种差异的原因之一。由于相对较低频的周期信息会湮没在噪声中,影响对周期的分析及确定[6],因此也有学者在分析地心运动周期性变化之前,利用低通滤波器或小波变换剔除高频信息的影响,再利用“干净”的信号分析地心运动规律[5-6]。但这一类方法不具有较强的自适应性,会对地心运动的周期分析造成一定影响。
针对信号混淆问题,如果可以采用一种自适应的盲源信号分解方法,剔除地心运动时间序列中的高频信息,分析重构后的干净时序,则可能会有更好的效果。经验模态分解方法(empirical mode decomposition,EMD)以其较强的自适应性,目前已被广泛应用于时间序列的信号分离等领域,并取得了良好的效果。如文献[11]运用EMD方法对微震信号降噪,效果明显;文献[12]利用EMD方法从GPS时间序列中分离出降水因素导致的准两年周期地表垂直形变;文献[13]证明EMD方法能有效分离出GPS信号中混杂的噪声信号,从而削弱噪声对结果的影响;文献[14]运用EMD和WD联合算法,分析了GPS水汽时间序列,并探测到各个GPS站均存在周年、半周年的周期震荡。
地心运动时序与GPS时间序列等类似,均混有高频信息的干扰,因此也可以利用EMD方法对地心运动时序进行预处理,对相对“干净”的时序进行分析。本文在现有研究的基础上,将EMD方法应用于地心运动时间序列分析领域;采用网平移法对IGS提供的GNSS周解进行解算得到2007-2017年间地心运动时间序列,对其进行分解重构,剔除高频项,并验证该方法的有效性;最后,利用重构后的时间序列对地心运动的周期和振幅作进一步的分析探讨。
1 地心运动的确定 1.1 网平移法利用IGS提供的2007-2017年GNSS周解数据,采用网平移法计算其与ITRF2014框架原点的平移量,得到地心运动时间序列。本文所使用的是Helmert七参数转换法,计算公式如下[7]
 (1)
(1) 式中,(x,y,z)为测站在ITRF2014框架下的坐标;(X,Y,Z)为测站坐标的GNSS周解;εx、εy、εz为旋转参数;s为尺度参数;Tx、Ty、Tz为平移参数,即地心位移量[15]。为提高计算精度,本文尽可能均匀地选取核心测站数据进行地心运动反演,并对粗差进行修复,对于时间序列中的缺失部分,采用三次样条插值方法补全。
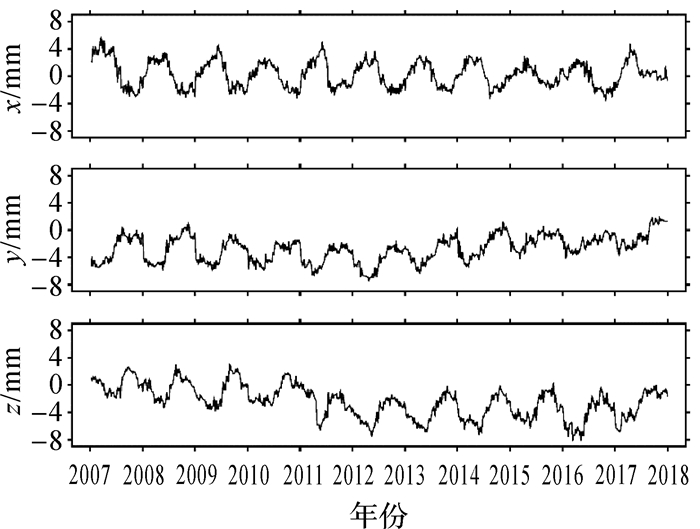
1.2 地心运动解算结果精度分析本文求解的地心运动时间序列如图 1所示。对所得地心运动结果的精度评价主要包括两方面:一方面Tx、Ty和Tz的标准偏差可作为其内符合精度[16];另一方面美国得克萨斯大学空间研究中心(CSR)提供的利用SLR数据(跟踪lageos1/2两颗卫星)进行动力法解算的地心运动序列是国际公认的最佳结果,可以参考此时间序列评定计算结果的外符合精度。表 1给出了地心运动时序主要信息,以及内、外符合精度统计。
|
| 图 1 地心运动时间序列 |
| mm | |||||
| 参数 | 最大值 | 最小值 | 平均值 | 内符合精度 | 外符合精度 |
| Tx | 5.81 | -3.60 | 0.27 | 1.94 | 3.06 |
| Ty | 1.83 | -7.55 | -2.75 | 1.95 | 3.31 |
| Tz | 3.05 | -8.28 | -2.39 | 2.39 | 4.78 |
从表 1中可以看出,地心运动的量级在3个方向均为毫米级,平均值分别为0.27、-2.75和-2.39 mm,内符合精度在2.5 mm之内,外符合精度在5 mm之内,精度较好,并且Tx、Ty方向的内、外符合精度均优于Tz方向。本文所计算的地心运动平均值和内外符合精度与CGS(centro de geodasia spaziale)采用几何法和动力法的计算结果[17]及文献[6-7]给出的统计结果相比较具有很好的一致性。
2 EMD方法重构地心运动时序高频信息会影响地心运动周期的分析及确定,在分析地心运动之前,应抑制噪声(即高频部分)的影响[6]。EMD方法是一种处理非线性非平稳信号的时频分析方法[18],它基于信号本身自适应地从高频到低频逐次分解,不需要任何的先验值,即可获得一组固有模态函数(intrinsic mode function,IMF)分量,这些模态函数能够很好地反映信号在任何时间局部的频率特征。EMD的基本思路是把时间序列x(t)根据原序列自身特征分解成若干个模态分量IMF和一个趋势项,表达式为
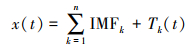 (2)
(2) 式中,Tk(t)为趋势项;IMFk为模态分量。
为了得到相对“干净”的时间序列,本文利用EMD方法按如下步骤对时序进行分解和重构[11, 13]:
(1) 将原始时序分解为k个IMF分量,并计算各IMF分量与原始序列的相关系数。
(2) 利用相关系数局部最小值原则确定高频项分界值,即一组相关系数中第一个取得局部最小值对应的IMF,记为IMFn。
(3) IMFn及IMFn之前的分量为高频项,将剩下的低频项(即周期项和趋势项之和)通过重构方法获得一组“干净”的时间序列。
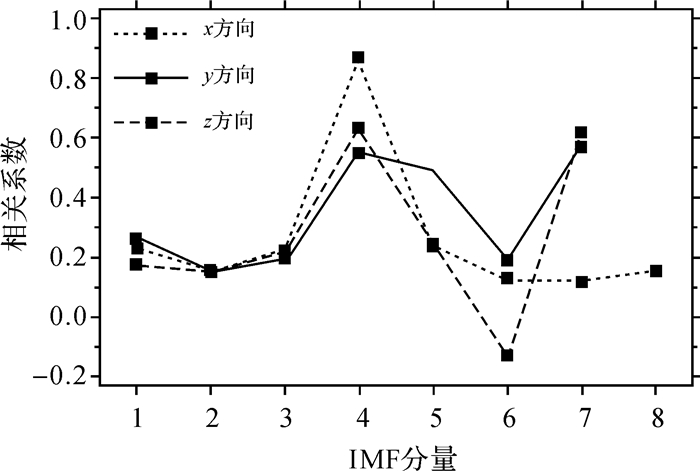
这种序列重构方法无需设定经验值判定高频项的分界值,避免了人为因素造成的误差,具有自适应性。各个方向对应各IMF分量与原始序列的相关系数如图 2所示,从图中可以看出Tx、Ty和Tz方向的分界层均集中在第2个IMF分量。Tx方向上与原序列一致性较好的是第4个IMF分量,相关系数接近0.9,Ty和Tz方向上与原序列一致性较好的是第4、7个IMF分量,相关系数在0.6以上。同时,每一个方向上的IMF分量的个数不同,Ty和Tz方向的IMF分量个数为7,而Tx方向有8个IMF分量,这说明EMD方法是根据原始序列的自身特征进行分解。
|
| 图 2 3个方向各个IMF分量相关系数 |
根据分界层及分界层之前的IMF为高频项的原则,对IMF3及之后的分量进行重构。Tx、Ty和Tz 3个方向重构序列分别如图 3(a)-(c)所示,其中图Ⅰ为重构前的时间序列和重构的低频项,图Ⅱ为分离出的高频项。

|
| 图 3 3个方向重构的时间序列 |
由图 3可知,原始序列与低频项具有良好的一致性,其包含的周期信息更为明显,这会使得周期振幅的分析结果更加可靠。去除高频项后Tx、Ty和Tz方向的振幅范围分别为:-4~4 mm、-7~1 mm、-8~2 mm。分离出的高频项(即IMF1和IMF2分量之和)均在0附近随机波动,周期性特征并不明显。
为了验证EMD方法抑制噪声的效果,可以通过计算重构时间序列占原序列的能量百分比[13],以及两者之间的相关系数这两个参数作为评价利用EMD方法重构地心运动时间序列效果的标准。表 2给出了3个方向EMD重构时间序列对应的相关系数和剩余能量百分比统计结果。
由表 2可以看出,重构时序与原序列的相关系数在95%左右,说明两者的符合度较好,保留了序列中较多的有效信息。重构后时间序列的剩余能量百分比均在90%以上,说明被剔除掉的基本上是能量较低的高频信息。综上所述,在利用基于EMD方法重构得到的时间序列进行地心运动结果分析时,可以在一定程度上减小高频信息的混入对结果的影响。
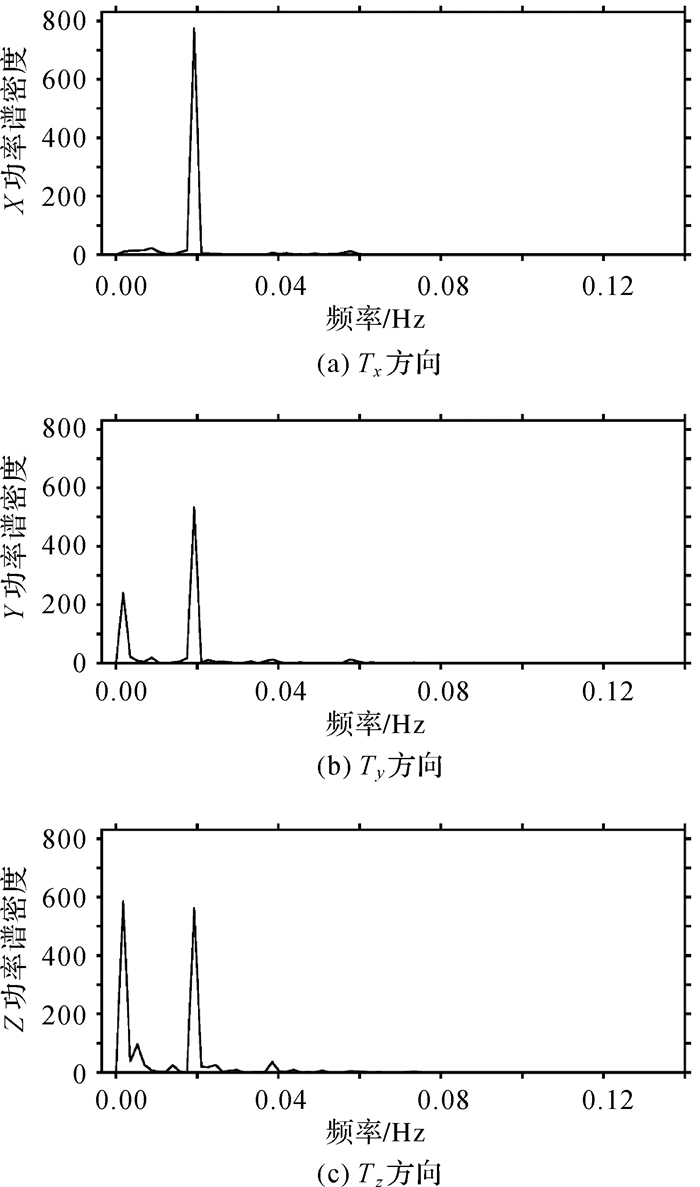
3 地心运动时间序列分析对重构的2007-2017年地心运动时序进行快速傅里叶变换,计算功率谱密度,由此识别周期,并计算每个周期的贡献率大小。图 4给出了Tx、Ty和Tz 3个方向的功率谱密度图(采样频率为7 d)。表 3给出了使用EMD方法重构地心运动变化时间序列前后各个周期的贡献率统计结果。
|
| 图 4 EMD重构时序在Tx、Ty和Tz方向功率谱密度 |
| Tx | 周期/d | 364 | 800 | 400 | 1334 | 121 |
| EMD后贡献率/(%) | 77.70 | 2.35 | 1.52 | 1.48 | 1.38 | |
| EMD前贡献率/(%) | 71.20 | 2.13 | 1.31 | 1.28 | 1.25 | |
| Ty | 周期/d | 364 | 4004 | 800 | 121 | 182 |
| EMD后贡献率/(%) | 54.03 | 24.50 | 2.38 | 1.83 | 1.37 | |
| EMD前贡献率/(%) | 49.96 | 23.29 | 1.76 | 1.62 | 1.12 | |
| Tz | 周期/d | 4004 | 364 | 1334 | 182 | 286 |
| EMD后贡献率/(%) | 37.99 | 36.40 | 6.18 | 2.31 | 1.66 | |
| EMD前贡献率/(%) | 35.37 | 35.21 | 5.95 | 2.05 | 1.59 |
从图 4中可以看到,3个方向上在0.019 Hz上(对应一年的周期)均有较高的能量出现,说明3个方向存在明显的周年变化;Ty和Tz方向在低频部分也有较大的能量,这说明Ty和Tz还存在较明显的长期变化项,并且Tz方向更为明显。从表 3可以看出,在利用EMD方法重构时间序列后,各主要周期的贡献率均有所提高,使得周期性特征的识别更加明显准确。经计算,Tx、Ty和Tz方向分别提高了12.3%、16.7%、6.3%。另外,Tz方向上的长周期变化趋势较Tx、Ty方向更为明显,其趋势项的贡献率在各周期贡献率中最高。
为了得到各个周期对应振幅和相位,结合最小二乘方法对重构后的时间序列进行拟合[5]
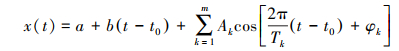 (3)
(3) 式中,x(t)为t时刻的地心运动;a为常数项;b为趋势项;t0为初始时间;A为振幅;φ为相位;m为周期个数;T为周期;A和φ为调和系数。地心运动周期性变化振幅和相位的拟合结果见表 4。
| Tx | 周期/d | 364 | 800 | 400 | 1334 | 121 |
| 振幅/mm | 2.32 | 0.40 | 0.32 | 0.31 | 0.30 | |
| 相位/(°) | -19.16 | 77.37 | 22.61 | 79.24 | -42.83 | |
| Ty | 周期/d | 364 | 4004 | 800 | 121 | 182 |
| 振幅/mm | 1.89 | 1.09 | 0.28 | 0.26 | 0.28 | |
| 相位/(°) | -6.02 | -74.58 | -37.35 | -19.18 | -43.08 | |
| Tz | 周期/d | 4004 | 364 | 1334 | 182 | 286 |
| 振幅/mm | 1.28 | 2.07 | 0.71 | 0.46 | 0.36 | |
| 相位/(°) | 48.73 | -11.78 | 79.50 | -50.94 | 9.94 |
现有研究表明,地心运动存在明显的周年项和相对较弱的半年项[9],这种变化主要与大气、海洋等质量再分布有关[1]。从表 4中可以看出,周年项与半周年项对应的振幅均为毫米级,并且周年项的振幅大于半年振幅,这与已有研究成果基本一致[2, 3, 6, 19]。Tx、Ty和Tz方向的周年项振幅均为各周期对应振幅的最大值,分别为2.32、1.89和2.07 mm。但Tz方向中周期贡献率最大的是4004 d,接近于本文的研究时间跨度,这说明了Tz方向的趋势项较明显,但Tz方向的周年变化贡献率与长期趋势的贡献率仅相差1.5%左右,因此,可以认为在Tz方向上也存在比较明显的周年变化。另外,从表 3中可以看出,3个方向的半年项均较弱,其中Tx和Ty方向上还存在4~6个月的震荡。研究表明,半年项周期具有时变性[6],这一特性的存在可能导致半年项的能量分布较为离散,从而导致这种周期震荡。
表 5列出了本文及相关学者求得的地心运动长期变化。相比于周期性运动,长期运动速度较小,Tx、Ty和Tz方向分别为-0.02、0.13和-0.27 mm/a。本文结果与现有研究基本一致,3个方向上的趋势性变化基本都在1 mm/a之内。另外,趋势项的绝对值在Tz方向上最大。
| (mm/a) | ||||
| 方案 | 时间跨度 | Tx | Ty | Tz |
| SLR[5] | 1993-2006 | -0.26±0.02 | 0.43±0.02 | 0.50±0.02 |
| CHAMP[6] | 2001-2006 | 0.495 | -0.004 | 1.309 |
| SLR直接法[7] | 1996-2000 | 0.14±0.25 | -0.39±0.31 | 0.79±0.75 |
| SLR动力法[7] | 1996-2000 | -0.09±0.19 | -0.07±0.24 | -0.01±0.91 |
| GPS[20] | 1996-2000 | 0.68±0.61 | -0.19±0.60 | -5.56±2.61 |
| 地球物理[21] | - | 0.13 | -0.33 | 0.81 |
| 本文方法 | 2007-2017 | -0.02 | 0.13 | -0.27 |
表 6为学者根据不同研究方法得出的振幅和相位与本文所得结果的比较。需要说明的一点是,由于Tx和Ty方向上的半年项都具有时变性,因此在统计这两个方向上的半年项时,本文根据表 4选取4~8个月长度的周期中振幅最大的一项,作为半年项的统计结果,即Tx方向为121 d,Ty方向为182 d。
| 方案 | Tx | Ty | Tz | ||||||
| 振幅/mm | 相位/(°) | 振幅/mm | 相位/(°) | 振幅/mm | 相位/(°) | ||||
| 周年项 | GPS, OBP, GRACE[2] | 2.1 | 242 | 3.4 | 144 | 2.6 | 207 | ||
| SLR[3] | 2.6 | 225 | 3.1 | 137 | 5.5 | 205 | |||
| SLR[5] | 2.3±0.2 | 290.7±5.7 | 1.0±0.3 | 135±19 | 0.8±0.2 | 235±10 | |||
| CHAMP[6] | 2.1 | - | 3.2 | - | 3.1 | - | |||
| GPS[9] | 1.93±0.2 | 269±6 | 2.49±0.1 | 324±3 | 1.98±0.3 | 114±8 | |||
| 本文方法 | 2.32 | -19.16 | 1.89 | -6.02 | 2.07 | -11.78 | |||
| 半年项 | GPS, OBP, GRACE[2] | 0.6 | 70 | 3.4 | 31 | 2.6 | 50 | ||
| SLR[5] | 0.8±0.2 | 317±13 | 0.6±0.1 | 170±19 | 0.6±0.2 | 28.9±13 | |||
| CHAMP[6] | 0.6 | - | 0.7 | - | 0.9 | - | |||
| SLR/CSR[19] | 0.8±0.5 | 192±13 | 0.3±0.5 | 174±19 | 1.2±0.6 | 197±12 | |||
| 本文方法 | 0.30 | -42.83 | 0.28 | -43.08 | 0.46 | -50.94 | |||
除了周年项和半周年项的变化,以及长期的运动趋势外,本文还探测到了其他的周期信息。Tx和Ty方向有800 d的周期,但Tz方向不存在;Tx和Tz方向存在1334 d的周期性变化,而Ty方向则不明显。这类周期变化被称为年际变化[6],其可能与地表水、大气、海平面和地幔对流等的不规则变化有关。
4 结语本文针对IGS提供的GNSS周解数据,采用Helmert七参数法计算了2007-2017年的地心运动时间序列,其内外符合精度均优于5 mm,与已有研究具有良好的一致性。采用EMD方法对时间序列进行分解重构,发现重构时序的高频信息得到有效抑制,周期贡献率有所提高。利用该序列求得的地心运动在Tx、Ty和Tz 3个方向的周年振幅分别为2.32、1.89和2.07 mm;半年项较小,且在Tx和Ty方向上具有时变性;此外探测发现还存在一些其他年际变化及小于1 mm/a的长期运动趋势。
| [1] |
VERNIER M, BAIL K L, BERIO P, et al. Geocentre motion measured with DORIS and SLR, and predicted by geophysical models[J]. Journal of Geodesy, 2006, 80(8-11): 637-648. DOI:10.1007/s00190-006-0079-z |
| [2] |
RIETBROEK R, FRITSCHE M, BRUNNABEND S E, et al. Global surface mass from a new combination of GRACE, modelled OBP and reprocessed GPS data[J]. Journal of Geodynamics, 2012, 59-60(5): 64-71. |
| [3] |
ALTAMIMI Z, COLLILIEUX X, MÉTIVIER L. ITRF2008:an improved solution of the international terrestrial reference frame[J]. Journal of Geodesy, 2011, 85(8): 457-473. DOI:10.1007/s00190-011-0444-4 |
| [4] |
杜彬, 杨强, 章传银, 等. GPS网平移法反演地心运动研究[J]. 导航定位学报, 2013, 1(2): 38-41. DOI:10.3969/j.issn.2095-4999.2013.02.009 |
| [5] |
郭金运. 由SLR观测的地心周期性运动1993-2006[J]. 测绘学报, 2009, 38(4): 311-317. DOI:10.3321/j.issn:1001-1595.2009.04.005 |
| [6] |
郭金运, 韩延本, 黄金维. 由CHAMP卫星监测的地球质心运动分析[J]. 中国科学(G辑), 2008(10): 1404-1413. |
| [7] |
秦显平, 杨元喜. 用SLR数据导出的地心运动结果[J]. 测绘学报, 2003, 32(2): 120-124. DOI:10.3321/j.issn:1001-1595.2003.02.005 |
| [8] |
杨强, 杜彬, 党亚民, 等. 利用SLR反演地心运动[J]. 导航定位学报, 2013, 1(2): 45-48. |
| [9] |
魏娜, 施闯, 刘经南. 利用GPS数据反演地心运动[J]. 武汉大学学报(信息科学版), 2011, 36(4): 441-445. |
| [10] |
LAVALLÉE D A, DAM T V, BLEWITT G, et al. Geocenter motions from GPS:an unified observation model[J]. Journal of Geophysical Research Solid Earth, 2006, 111: B05405. |
| [11] |
贾瑞生, 赵同彬, 孙红梅, 等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报, 2015, 58(3): 1013-1023. |
| [12] |
PAN Y, SHEN W B, DING H, et al. The quasi-biennial vertical oscillations at global GPS stations:identification by ensemble empirical mode decomposition[J]. Sensors, 2015, 15(10): 26096-26114. DOI:10.3390/s151026096 |
| [13] |
张双成, 何月帆, 李振宇, 等. EMD用于GPS时间序列降噪分析[J]. 大地测量与地球动力学, 2017, 37(12): 1248-1252. |
| [14] |
王笑蕾, 张勤, 张双成. 基于EMD和WD联合算法的GPS水汽时间序列的周期性振荡分析[J]. 武汉大学学报(信息科学版), 2018, 43(4): 620-628. |
| [15] |
魏娜, 施闯, 耿长江, 等. 参考框架的HELMERT转换[J]. 大地测量与地球动力学, 2010, 30(4): 109-112. |
| [16] |
吴斌, 彭碧波, 许厚泽. 地心变化的测定[J]. 科学通报, 1999, 44(10): 1106-1108. DOI:10.3321/j.issn:0023-074X.1999.10.020 |
| [17] |
DEVOTI R, FERMI M, SCIARRETTA C, et al. CGS geocenter time series from SLR and GPS data[J]. Iers Technical Note, 1999, 25: 41-46. |
| [18] |
HUANG E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time seris[M]. [S.l.]: The Royal Society, 1998.
|
| [19] |
赵德军, 李潭欣, 李婧, 等. DORIS、GPS和SLR空间大地测量技术导出的地心运动规律[J]. 测绘工程, 2015, 24(12): 21-24. DOI:10.3969/j.issn.1006-7949.2015.12.005 |
| [20] |
郭海荣, 杨元喜, 焦文海. 地心运动时间序列的抗差谱分析[J]. 测绘学报, 2003, 32(4): 308-312. DOI:10.3321/j.issn:1001-1595.2003.04.005 |
| [21] |
MÉTIVIER L, LEFFTZ M G, ALTAMIMI Z. On secular geocenter motion:the impact of climate changes[J]. Earth & Planetary Science Letters, 2010, 296(3): 360-366. |


