交通流量分配是路网交通规划的重要组成部分。灾后路网遭到部分损毁,原有的交通分配方案已不再适用,为开展灾后疏散与救援工作,保证灾区的正常交通运输,灾后管理已成为国内外的研究热点[1-4]。
灾后救援与交通流量再分配需考虑路径规划问题。文献[5]提出的蚁群算法是一种解决组合优化问题的启发式搜索算法,蚂蚁通过信息素进行交流,在不同的节点中选择性转移,从而得到最优路径。蚁群算法在路径规划、车辆调度[6]、集成电路设计[7]等问题中都取得了不错的结果,在交通分配方面同样得到广泛应用[8]。文献[9]量化路段薄弱性和重要性,计算路段关键度,并实现路网交通流量的重分配。文献[10]通过分析车流经过交叉口的延误时间改进蚁群算法,并应用于交通分配中。文献[11]将蚁群系统与可变邻域搜索相结合,应用改进的蚁群算法解决车辆路径规划问题。
路网的通行能力是制约交通流量的关键,当前研究多以定性为主,缺乏定量化与体系化的研究,交通分配评估通行能力时缺乏综合性指标分析,用于灾后交通路网部分损坏情况的流量分配研究较少。因此,本文提出一种基于改进蚁群算法的交通流量分配方法,以长株潭地区为例,在基本算法的基础上引入道路质量评价体系,以评价结果作为启发式因子;同时利用路段交通流量改进信息素的更新机制,加入扰动节点,以避免陷入局部最优解。最后以长株潭地区交通流量分配进行试验,结果表明改进算法能较好地模拟交通流量分配情况。
1 道路质量评价体系影响路网通行能力的因素主要包括路网结构和路网容量两方面。路网结构又分为功能结构、等级结构和布局结构[12],路网容量由各等级道路交通量决定。因灾后路网受损的特殊情况,车辆行驶路径应保证等级结构合理性、功能结构稳定性和高可达性,因此本文提出道路质量评价体系,利用变异系数法为路段基础数据如路段等级、设计时速等指标分配权重,综合评价路段通行能力,评价结果即为路段质量。
道路质量评价体系中各项指标意义不同,先将原始指标无量纲化处理,取不同指标的变异系数用于衡量各项指标的差异程度,最后得到各指标Zi的权重ωi,并计算不同路段质量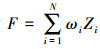
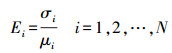 (1)
(1) 式中,Ei表示指标Zi的变异系数;σi为规范化处理后指标Zi的标准差;μi为规范化处理后指标Zi的平均值。
对于权重ωi[13],有
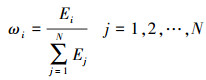 (2)
(2) 变异系数法是一种完全客观的赋权方法,用于评价指标模糊且缺少专家经验的情况。不同路段的质量评价结果差异明显,路段质量将作为启发式因子用于改进算法,实现路网的交通流量分配。
2 改进的蚁群算法针对基本蚁群算法运行慢、早熟收敛、易陷入局部最优解的问题[14],同时考虑灾后城市间交通流量的实际情况,为提高算法的有效性,本文对基本算法进行了相应改进。
2.1 考虑道路质量的启发式因子改进基本蚁群算法中蚂蚁根据信息素和启发因子选择下一个城市,转移概率公式[5]为
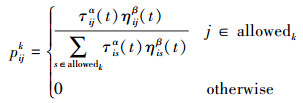 (3)
(3) 式中,k表示当前蚂蚁编号;τij(t)表示t时刻路段ij的信息素;α表示信息素影响程度;ηij(t)表示t时刻路段ij的启发式因子;β表示启发式因子影响程度;allowedk表示第k只蚂蚁可选择节点的集合。
启发式因子ηij反映蚂蚁从节点i转移到节点j的启发程度,一般情况下为该路段长度的倒数。本文引入道路质量评价体系,其结果F有ηij=F,反映路段通行能力,由路段行政等级、设计时速、车道数量、年平均日交通量4个指标衡量。路径为起终点间被选择路段的有序集合,路径质量即为路段质量之和,路径质量越好,通行能力越强,该条路径越易被选择。
2.2 避免陷入局部最优解蚁群算法中信息素τij反映走过的路段长度,n时刻后更新[5]如下
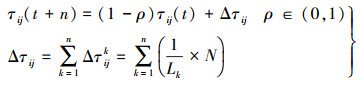 (4)
(4) 式中,ρ表示信息素蒸发参数;Δτij表示路段ij的信息素增量;Lk表示蚂蚁k走过的路段长度;N为常数。
针对基本蚁群算法易陷入局部最优解的问题,设置监控阈值num,当路段ij被选择次数超过num时,引入随机节点c,同时改进原路段ij信息素更新机制。在保证信息素的影响下将搜索范围扩至全局,这样的扰动增强了算法的随机搜索,在一定程度上避免了局部发生停滞的问题。
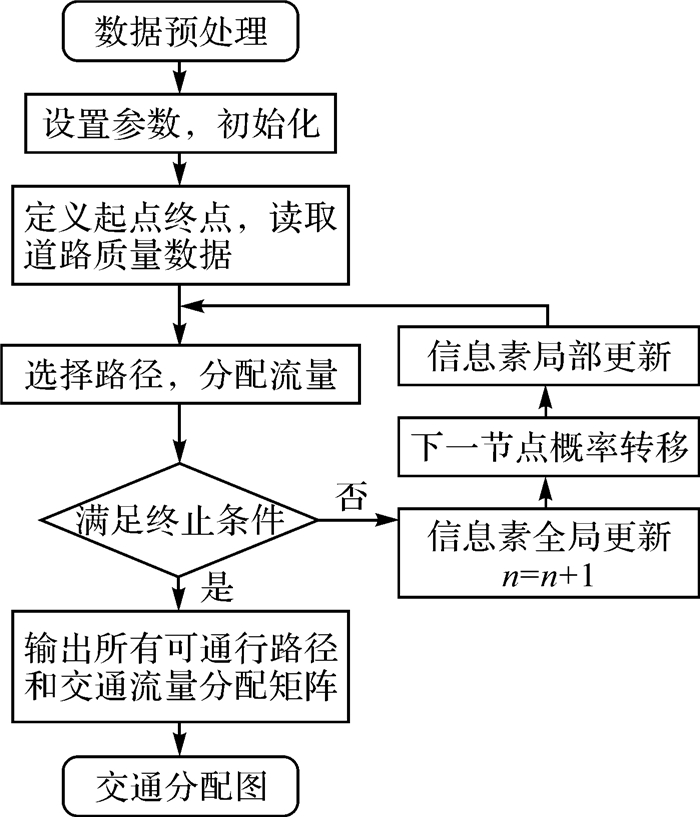
3 改进的蚁群算法用于交通流量分配基于改进蚁群算法的交通流量分配方法流程如图 1所示。
|
| 图 1 基于改进蚁群算法的交通流量分配方法流程 |
(1) 数据预处理:以市县区为单位划分节点,确定节点数目N,根据道路质量评价体系求得路段质量F。
(2) 设置参数:由交通需求总量确定蚂蚁数目M、循环次数C,使交通总量等于M×C,确定转移公式中的α、β、ρ;信息素τij初始为路段ij长度的倒数;起点区域为FIRST,终点区域FINAL。
(3) 选择路径:令n=1,M只蚂蚁从FIRST出发,根据式(4)选择下一节点。引入参数q0,q0决定了蚂蚁转移时选择已有经验还是选择探索新路径。选择下一个节点时,产生随机数q,q≤q0时选择allowedk中转移概率最大的节点;q>q0时采用轮盘赌法,计算不同路段的概率累积量,转移的方向即为q所在概率区间的节点
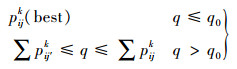 (5)
(5) 判断路段ij被选择次数是否达到监控阈值num,未超过则按式(4)更新该路段的信息素τij;若超过num则开发新路段,引入随机节点c,此时转移概率为
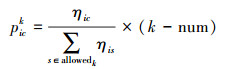 (6)
(6) 新路段ic信息素按式(4)更新,原路段ij信息素更新为
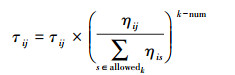 (7)
(7) (4) 分配流量:迭代处理时保证每只蚂蚁都能找到FINAL,使交通量完全分配到路网中,记录所有可通行路径和路径被选择的重复次数。
(5) 判断n是否与C相等,不等则n=n+1。更新每次循环中最优路径的信息素,信息素的全局更新公式为
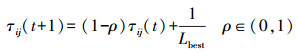 (8)
(8) 式中,Lbest表示本次循环全局最优路径的长度。全局更新方法扩大了最优解与普通解间的信息素差异,加快了算法收敛。随后将M只蚂蚁重置于FIRST,重复步骤(3)—(5),直至满足终止条件。
(6) 完成交通总量的全部分配,输出所有可通行路径、路径重复次数和路段的交通流量,得到路网交通流量分配图。
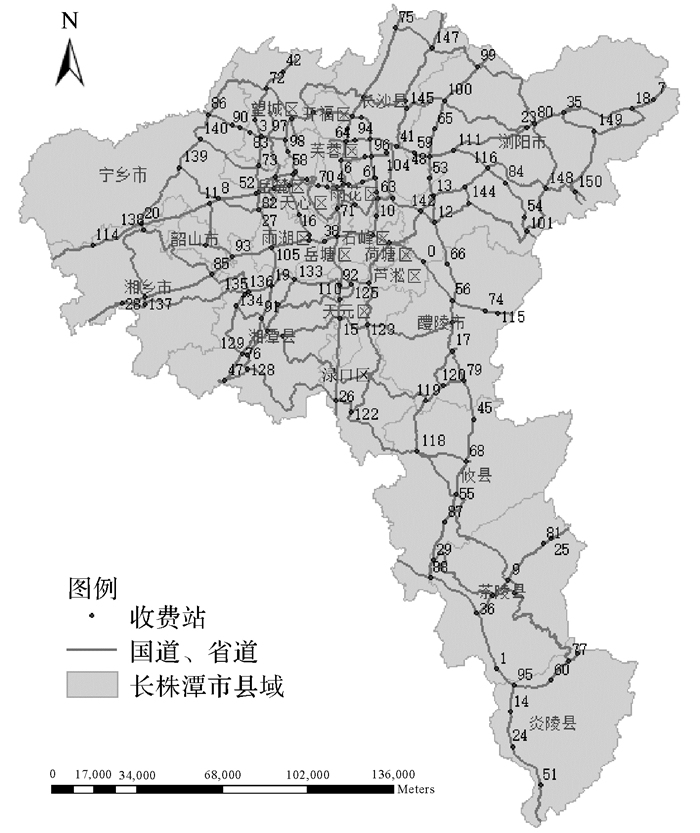
4 试验结果与分析本文以长株潭地区23个市县区为例,路网分布如图 2所示。将151个收费站按地理位置所属市县区进行划分,建立收费站与路段的关联关系。
|
| 图 2 长株潭地区公路交通分布 |
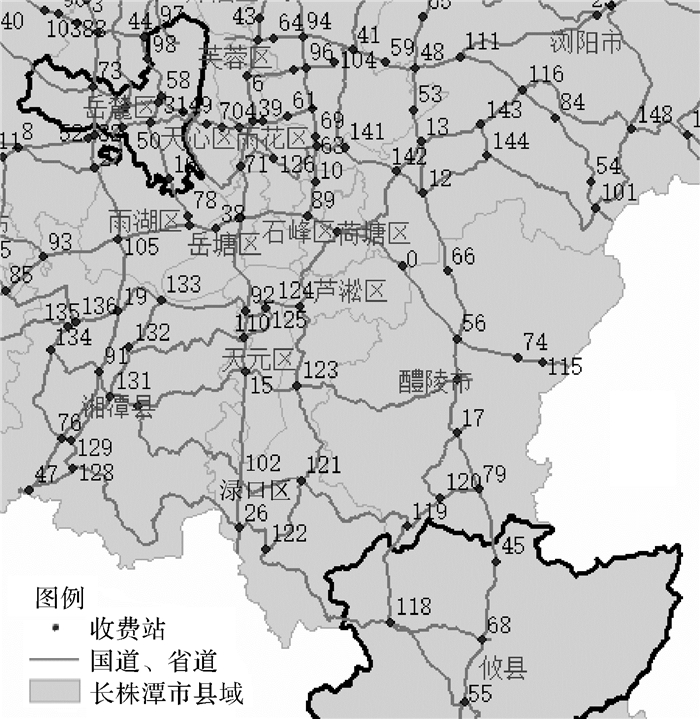
参数初始化:N=151,M=151,C=20,α=1,β=1,ρ=0.1,本文1只蚂蚁记为1个交通量。输入路段长度和路段质量,起点区域为攸县,终点区域为岳麓区,如图 3所示。
|
| 图 3 起始区域为攸县、终点区域为岳麓区 |
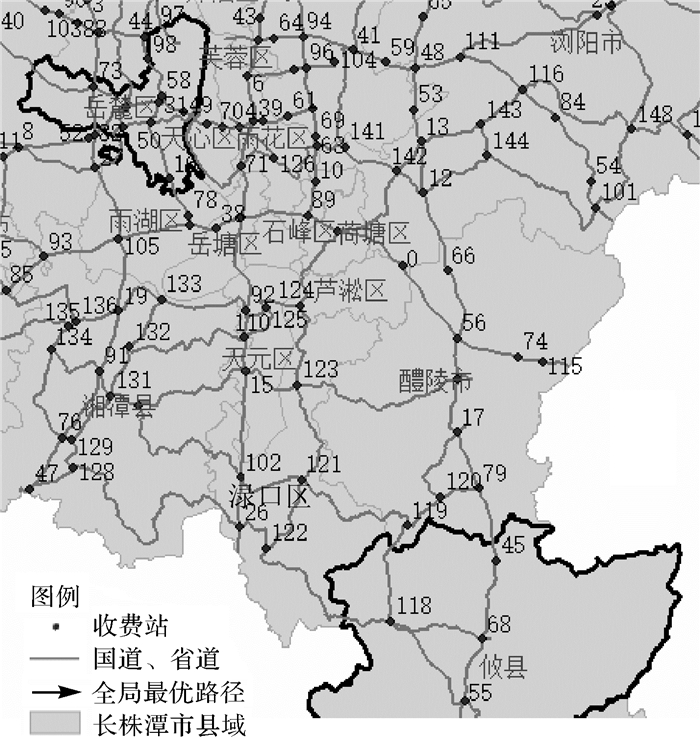
运行算法,得到起点终点区域间所有可通行路径、全局最优路径和各路段的流量,全局最优路径如图 4箭头所示。
|
| 图 4 全局最优路径 |
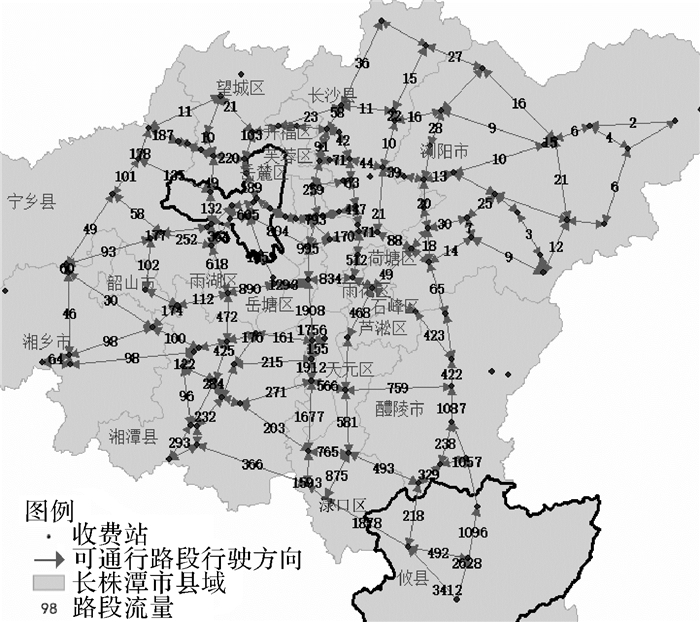
由于货车、客车等各种机动车所占空间不同,运输能力相差悬殊,路网能容纳的交通量随机动车种类不同而变化,因此需要将不同车型交通量统一为标准车型交通量。《城市道路工程设计规范》(CJJ 37—2012)明确了不同车型在以小客车为标准车型时的换算系数[15]。将各种车型交通量换算成小客车当量从而确定交通需求总量,算法结束后各路段分配的交通量可通过换算系数得到不同车型流量。各路段交通流量分配如图 5所示,箭头方向表示车辆行驶方向,路段上的数字即为该路段分配得到的交通量。
|
| 图 5 各路段交通流量分配 |
结果包含两区域间所有可通行路径和每条路径的重复次数,重复次数反映了不同路径被选择的概率。重复次数最大的路径通行能力最好,可以成为灾后救援的首选路径。
起点区域为攸县,终点区域为岳麓区时,不同蚁群算法选择出的全局最优路径及各自重复次数、路径流量见表 1。
| 算法 | 全局最优路径 | 重复次数 | 路径流量 |
| 基本蚁群算法 | 55—68—45—79—17—109—56—0—2—89—30—38—33—78—16—50 | 61 | 22435 |
| 改进算法 | 55—118—122—26—102—15—110—92—30—38—33—78—16—50 | 233 | 30531 |
| 精英蚁群算法 | 55—118—122—26—102—15—110—92—30—38—33—78—16—50 | 415 | 59238 |
根据路段质量得知,基本算法的全局最优路径质量为22.738,改进算法的全局最优路径质量为31.879,说明后者的通行能力更好,能承载更大的交通流量。表中“重复次数”和“路径流量”的数据也验证了改进算法的路径优于改进前。精英蚁群算法也是对基本算法的改进,算法效率有较大提高。但从表中可知,精英算法选出的全局最优路径和改进算法一致,但路径流量太大,早熟收敛,不符合流量分配要求。因此本文改进算法在路径选择上更合理。
改进算法提高了结果的有效性。所有可通行路径中最优与次优路径见表 2。两条路径的前9个节点相同,第10个节点发生分歧。路段30—38与路段30—71质量相近,但路段30—38长度远小于30—71。更多的蚂蚁综合考虑路段质量和路段长度两方面因素,因此第10个节点选择了38为后继节点。通过计算得到最优路径的质量大于次优路径,表 2路径流量对比也证实了最优路径的可靠性,因此算法选择的最优路径可以成为灾后救援的首选。分析表明,改进算法通过质量差异有效区分了不同的可通行路径,路径质量不同承载的流量也不同。
| 路径 | 重复次数 | 路径流量 | |
| 最优路径 | 55—118—122—26—102—15—110—92—30—38—33—78—16—50 | 233 | 30531 |
| 次优路径 | 55—118—122—26—102—15—110—92—30—71—50 | 134 | 25002 |
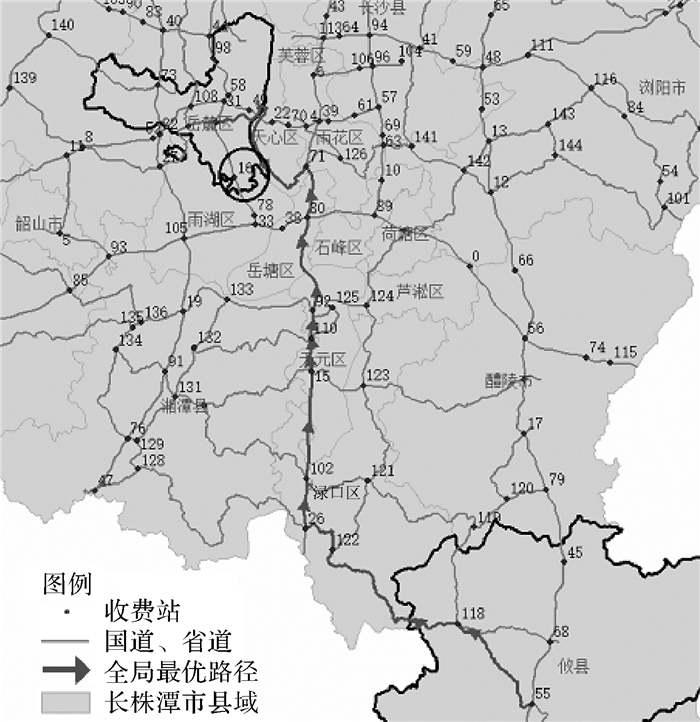
改进算法能较好地应对灾后路网损毁的情况。假设图 6中圆圈部分灾后损毁,可通行路径数目减少,受灾前两区域间共111条可通行路径,受灾后有88条可通行路径,灾后的全局最优路径变为灾前选择出的次优路径,如图 6箭头所示路径。包含节点16的路径受灾后不能通行,这些路径的流量按概率转移到其他路径上,灾后流量分配如图 7所示。
|
| 图 6 受灾后的全局最优路径 |
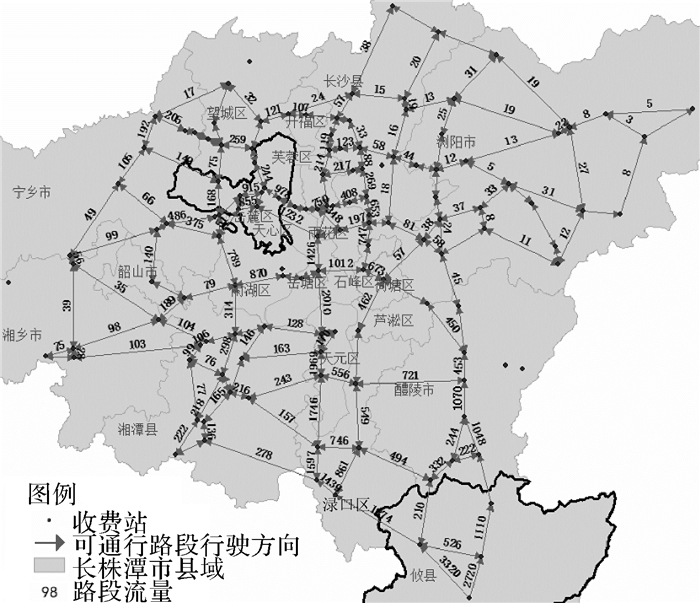
|
| 图 7 受灾后各路段交通流量分配 |
路段16—50和路段16—78灾后不能通行,两条路段位于岳麓区和雨湖区,部分相关路段灾前灾后交通流量变化见表 3。分析得到,改进算法考虑路段通行能力,将不能通行路段的流量分配到其他路段上,通行能力较强的路段承担流量较多,体现了算法处理灾后流量分配问题的适用性和合理性。
| 所属区域 | (部分)路段 | 灾前流量 | 灾后流量 | 路段质量 |
| 岳麓区 | 71—50 | 804 | 1232 | 42.377 |
| 31—50 | 605 | 855 | 32.962 | |
| 雨湖区 | 38—78 | 1293 | 1426 | 39.181 |
| 105—27 | 618 | 789 | 32.495 |
本文通过对路网通行能力的分析,提出了一种基于改进蚁群算法的交通流量分配方法,利用路段行政等级、车道数量、设计时速、路段年平均日交通量4个指标建立了道路质量评价体系,改进了启发式因子和信息素更新机制,提高了算法的有效性,算法结果能为救援工作和灾后路网交通运输分配决策提供建议和支持。但本文未考虑随时间推移流量增加对路网的影响,同时由于增加了“道路质量”这一因素,算法效率有待提高,后续会进一步研究时间因素对交通分配的影响及算法效率提高的问题。
| [1] |
BRACHMAN M L, DRAGICEVIC S. A spatially explicit network science model for emergency evacuations in an urban context[J]. Computers Environment & Urban Systems, 2014, 44(24): 15-26. |
| [2] |
HAMZA-LUP G L, HUA K A, PENG R, et al. A maximum-flow approach to dynamic handling of multiple incidents in traffic evacuation management[C]//Proceedings of IEEE Intelligent Transportation Systems. Vienna: IEEE, 2005: 1147-1152.
|
| [3] |
蒲国利, 苏秦, 王修来. 满足救灾需求的灾后救援供应链网络设计[J]. 工业工程与管理, 2015, 20(6): 161-166. DOI:10.3969/j.issn.1007-5429.2015.06.023 |
| [4] |
俞武扬. 基于交通阻断情景的应急资源布局问题研究[J]. 自然灾害学报, 2013, 22(3): 99-103. |
| [5] |
DORIGO M, MANIEZZO V, COLORNI A. Ant system:optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems Man & Cybernetics-Part B:Cybernetics, 1996, 26(1): 29-41. |
| [6] |
SAIDI-MEHRABAD M, DEHNAVI-ARANI S, EVAZABADIAN F, et al. An ant colony algorithm (ACA) for solving the new integrated model of job shop scheduling and conflict-free routing of AGVs[J]. Computers & Industrial Engineering, 2015, 86(C): 2-13. |
| [7] |
AKBARI M, SHOKOUHIFAR M, HASHEMIPOUR O, et al. Systematic design of analog integrated circuits using ant colony algorithm based on noise optimization[J]. Analog Integrated Circuits and Signal Processing, 2016, 86(2): 327-339. DOI:10.1007/s10470-015-0682-0 |
| [8] |
SANTOS L, COUTINHO-RODRIGUES J, CURRENT J R. An improved ant colony optimization based algorithm for the capacitated arc routing problem[J]. Transportation Research Part B Methodological, 2010, 44(2): 246-266. DOI:10.1016/j.trb.2009.07.004 |
| [9] |
张建旭, 蒋燕. 基于局部路网交通流重分配的路段关键度计算[J]. 交通运输系统工程与信息, 2016, 16(1): 105-110. DOI:10.3969/j.issn.1009-6744.2016.01.017 |
| [10] |
常玉林, 汪小渟, 张鹏. 改进蚁群算法在交通分配模型中的应用[J]. 郑州大学学报(工学版), 2017, 38(2): 41-44. |
| [11] |
ZHAI L L, ATHER I M, WANG Z J, et al. Improved ant system algorithm and its application for vehicle routing problem[C]//Proceedings of the 2nd Workshop on Advanced Research and Technology in Industry Applications (WARTIA-16). [S.l.]: Atlantis Press, 2016.
|
| [12] |
程生平, 曹苏陇, 张巍. 城市路网结构体系分析与应用[J]. 城市道桥与防洪, 2017(5): 1-4. |
| [13] |
ZHAO W, LIN J, WANG S F, et al. Influence of human activities on groundwater environment based on coefficient variation method[J]. Environmental Science, 2013, 34(4): 1277-1283. |
| [14] |
付梦家, 游晓明. 多机器人系统及其路径规划方法综述[J]. 软件导刊, 2017, 16(1): 177-179. |
| [15] |
中华人民共和国住房和城乡建设部.城市道路工程设计规范: CJJ 37—2012[S].北京: 中国建筑工业出版社, 2016: 9-13.
|


