差分层析SAR(differential TomoSAR,D-Tomo SAR)成像技术[1]是层析SAR技术的扩展,由F.Lombardini在2005年提出。层析SAR可以获取目标的空间三维(方位-距离-高度)信息,实现了三维成像能力,但是同一个方位向-距离向分辨单元内不同散射元的高度变化信息被视为相位误差而补偿掉了,因此无法获取形变信息。差分干涉技术[2](differential InSAR, D-InSAR)虽然可以获取目标的形变信息,但是该技术是在InSAR技术[3]基础上发展而来的,故而没有摆脱InSAR中高度向分辨能力缺失的问题。相比较层析SAR成像技术和差分干涉技术,差分层析SAR成像技术对同一目标进行不同空间、时间位置的多次观测,在保持传统SAR方位-距离向合成孔径的同时,在斜距垂向(normal-slant-range, NSR)-形变速率平面内形成二维合成孔径,获得高程向和形变速率向的分辨能力,实现了对目标方位-距离-高度-时间四维成像。该技术的特点对实现城市基础设施动态形变监测、古建筑的风险评估、森林监测预评估、重要工程安全监测等应用[4-8]具有重要的实际意义和应用价值。
本文从差分层析SAR技术的成像原理、数据处理、成像算法等几个方面,对差分层析SAR技术的发展现状进行综合分析,并对其在城市形变监测预警、提取森林垂直结构信息、地下水位季节性变化监测、考古学、冰川运动等领域的应用潜力进行研究与阐述,对差分层析SAR技术目前存在的问题及发展趋势进行分析。
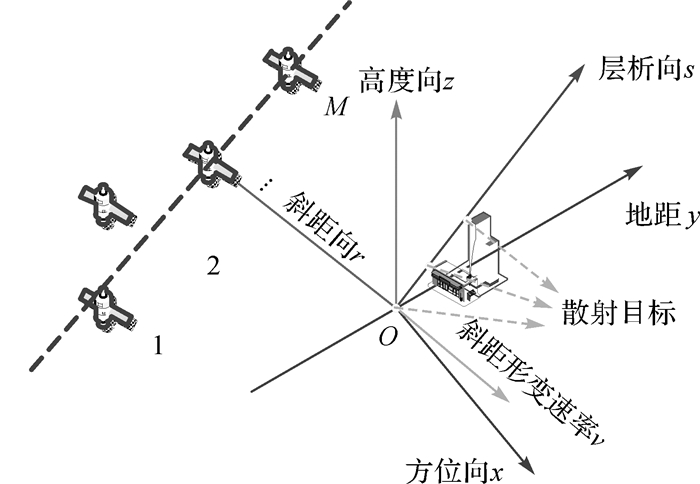
1 差分层析SAR成像原理差分层析SAR成像示意图如图 1所示,x为方位向,y为距离向,s为层析向,垂直于方位向-斜距向平面,v为形变速率向。假设在不同位置、时间对同一成像区域进行M次观测,经过方位向-距离向的二维压缩得到M幅SAR单视复(single light complex, SLC)图像, 从中选取一幅图像作为主图像,其他图像以主图像为标准进行配准、去斜后,得到图像方位向-距离向分辨单元的复序列,可表示为[9]
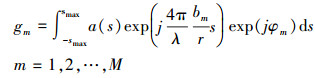 (1)
(1)
|
| 图 1 差分层析SAR成像 |
式中, [-smax, smax]为斜距垂向跨度;a(s)为目标的雷达散射特性函数;λ为波长;r为主图像斜距;bm为航过影像与主图像的垂直基线;φm为层析向采样点处斜距形变速率向的相位项。
在线性形变模型下,相位项φm表示为
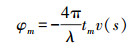 (2)
(2) 式中,tm为航过影像与主图像的时间基线;v(s)为线性斜距形变速率。将式(2)代入式(1)中,有
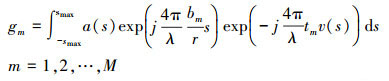 (3)
(3) 若令
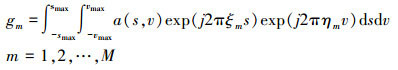 (4)
(4) 式中,[v-max, vmax]为形变速率的跨度;
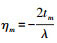
根据式(4)可知,差分层析SAR的观测数据为雷达散射特性函数在高度向—形变速率向的二维联合谱,通过成像算法反演求出目标信号的散射函数值,根据函数值的位置确定散射点在层析向的位置及形变速率向的大小,实现差分层析SAR的四维成像。
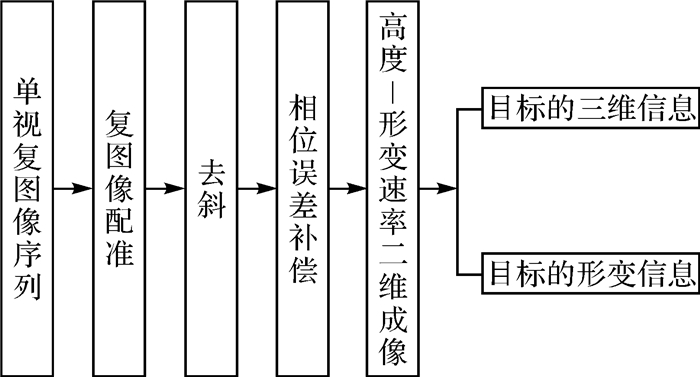
为获得差分层析SAR成像结果,首先获取序列二维SAR影像,通过对时序SAR影像进行复图像配准、去斜、相位误差补偿等处理,利用成像算法(如谱估计算法、压缩感知算法等)进行聚焦处理,从而得到层析向聚焦结果,获取高度及形变速率二维成像结果,最终得到观测目标的三维结构信息和形变信息。差分层析SAR成像流程如图 2所示。
|
| 图 2 差分层析SAR成像处理流程 |
获取SAR图像时由于观测几何的差异,导致相邻图像间存在一定的变形,为了将对应的同名地物在二维图像像素序列中对齐,需要对图像进行配准处理。图像配准是SAR数据处理过程中最关键的一步,直接影响到后续的产品质量,因此图像配准这一步骤显得尤为重要。已有的配准方法主要有3类,相关函数法[11]、波动函数法[12]、最大频谱法[13],另外还有一些混合改进算法即基于图像特征的配准算法[14]。但是这3类算法主要是针对某一类型的图像进行配准,对其他数据不具有普适性和稳健性。后来王青松、瞿继双等提出了联合实、复相关函数的图像配准方法[15],可以稳健、高效地适应于各类实测数据的处理。
1.2 去斜去除中心斜距引起的相位项的操作过程称为去斜。观测和待估参数间的频谱关系基于主图像中心斜距相位去除建立,因此去斜操作在差分层析处理中起着至关重要的作用。最为直接的去斜方法是利用雷达记录的电磁波传输延迟[16-17]进行去斜,但是该方法受大气扰动影响,会引入额外的大气相位误差。目前通过实测数据验证,基于模拟干涉相位的去斜方法[18]可以得到较为理想的去斜效果,该方法避免了额外相位误差的引入, 并且使用低精度的地形数据即可获得高精度的去斜效果,提高了成像精度。
1.3 相位误差补偿在差分层析中,相位误差主要是由大气扰动及地表形变等因素引起的,同时相位误差具有较强的随机性,对成像性能有严重影响。针对这一问题进行研究,研究者提出了多时相差分干涉技术(multitemporal differential interferometric SAR,MT-DInSAR)[19],它是地表形变检测的一种手段,可以得到大气相位的估计,因此通常作为一种相位误差补偿方法,但是处理方法繁琐。文献[20]在永久散射体干涉测量(permanent scatterer InSAR, PS-InSAR)技术基础上,基于相位误差的空间相关性,提出PS-InSAR中间输出量的相位误差补偿方法,成像结果有所改善,但受去斜方法的限制,适应性差,无法进行高精度补偿; 基于这一问题,文献[21]又提出一种PGA(phase gradient autofocus)相位误差补偿方法,算法简单,计算效率高,不受去斜方法的限制,具有良好的适应性。
1.4 高度-形变速率二维成像目前,差分层析SAR的观测数据通常由SAR系统的重轨飞行任务获得。在设计之初并未考虑差分层析的应用需求,获取的观测数据为空间-时间二维孔径的稀疏采样。在稀疏采样数据下,基于傅里叶变换方法得到的成像效果很不理想,不仅旁瓣高,而且分辨率低。文献[21]中孙希龙提出一种基于时空相关系数的二维稀疏孔径性能的评价准则,以求获得较优的系统性能,但是不能从实际上改善成像效果的缺失,因此利用稀疏分布的采样数据实现高度-形变速率向的二维成像是差分层析的难点问题。
2 差分层析SAR成像算法研究本文主要介绍目前差分层析SAR技术中常用的3种成像方法:传统的傅里叶变换算法、空间谱估计算法、压缩感知算法。对于目前的四维SAR成像系统,获取得到的观测数据在基线-时间平面内是稀疏且不均匀的,因此,用传统的傅里叶变换算法得到的成像结果受到高旁瓣影响,分辨率低,容易受到噪声影响,成像效果差。频谱估计算法成像效果优于傅里叶变换算法,分辨率得到了提升,但是成像处理过程中会进行大量矩阵运算,同时需要处理矩阵的病态问题,计算量大,过程烦琐。而压缩感知成像算法的提出,改善了成像效果,在低采样数据的情况下,将稀疏信号进行重构,在保持方位向-距离向分辨率的同时实现高度向-形变速率向的高分辨率成像。
2.1 傅里叶变换算法2000年,文献[22]首次成功地采用傅里叶变换的算法,实现了极化机载合成孔径雷达层析成像,对德国Oberpfaffenhofen地区进行成像试验,获得高度向为2.9 m的分辨率。随后,研究者将傅里叶变化算法应用到差分层析中,但是没有获得较高分辨率的成像效果。文献[23]对观测数据进行二维傅里叶变换来恢复散射体高度-速率维成像,因强副瓣存在,衰减情况不理想,成像效果很差。文献[21]基于傅里叶变换的成像方法,采用Envisat数据对意大利Naples地区和对美国Anaheim地区进行仿真成像处理,随着散射元数目的增多、观测数的减少,旁瓣变高,不能实现高分辨率成像。2014年,文献[6]利用28张超分辨率CSK数据,对意大利的Naples圣保罗体育场进行形变监测,时间跨度1年(形变速率分辨率为15 mm/a),瑞利高度分辨率为6 m。
在基线和时间均匀采样的条件下,二维傅里叶变换可获得满意的结果。然而实际条件下,傅里叶变换受到基线和时间数目较少、采样不均匀的影响,同时需要满足奈奎斯特采样定理[24],导致傅里叶变换效果差,旁瓣高,无法实现高分辨率成像。
2.2 空间谱估计算法2005年,文献[1]最早提出了差分层析成像概念,并采用Capon谱估计法成像,该方法具有高度-形变速率向的高分辨率,但是处理过程中需要使用多视数据估计观测协方差矩阵,降低了方位向-距离向的分辨率且旁瓣高,适用性差。基于奇异值分解(singular value decomposition, SVD)的成像方法[25]计算量大,同时需要处理奇异值矩阵的病态问题。2010年,提出基于Wiener型的正则化奇异值分解法[26],并且扩展到四维成像方法上。随后,任笑真提出一种基于逆问题的Backus-Gilbert成像算法[23],并利用Tikhonov正则化获得逆问题的正则解。奇异值分解法和逆问题求解成像算法虽都保持了方位向-距离向分辨率,但高程向-形变速率向分辨率依然较低。为改善高程向-形变速率向分辨率较低的问题,2012年,文献[27]提出基于RELAX算法的差分层析成像算法,该算法是在CLEAN算法基础上发展起来的一种基于非线性最小方差(nonlinear least squares, NLS)准则的高分辨谱估计算法,RELAX算法对噪声不作任何限定性假设,具有较强的适应性和稳健性,可以在保持方位向-距离向分辨率的同时实现高度向-形变速率向的高分辨率成像。
空间谱估计算法的提出,改善了基于传统傅里叶变换聚焦算法的成像效果,实现了超分辨率[28-29],但是这种成像方法也存在局限性,需要使用多视数据估计观测的协方差矩阵,而多视处理会降低方位向-距离向分辨率。
2.3 压缩感知算法压缩感知(compressive sensing, CS)理论[30-31]由数学家Donoho、Candes和Tao等提出, 根据CS理论,其核心内容为:在满足一定条件时,即使观测样本有限,稀疏信号也可以通过解一个非线性最优化问题而实现准确或近似重构。
2011年,朱小香将压缩感知理论应用到差分层析SAR成像技术中,采用TerraSAR-X影像对Las Vegas会议中心区进行四维成像处理,试验采用两种方法:CS算法和基于Wiener型的奇异值分解方法[32],通过分析得出CS算法可以分辨出间隔距离较近的散射体,高度向上的分辨率达到2 m,从而验证了CS算法的性能。2012年,孙希龙采用基于压缩感知的方法进行差分层析成像,得出在实际采样和典型噪声水平情况下,相比SVD、RELAX方法,压缩感知方法的分辨能力有较大的提升,验证了基于压缩感知的差分层析成像方法的有效性[33]。同年,任笑真提出一种新的四维成像方法——加权压缩感知(weighted compressive sensing),该方法的基本原理是考虑高频雷达应用中实际目标空间的稀疏结构,利用雷达方位角的稀疏分布和方位角距离压缩后的信号形式构造基阵和测量矩阵。并将加权矩阵引入到优化问题中,以减少噪声的影响,模拟数据的结果证实了成像方法的有效性[34]。文献[35]提出基于贝叶斯压缩感知的成像方法,随着噪声的增加,该方法的性能可以得到保持,有效避免了虚假目标的增加及散射中心的丢失,即使在低信噪比情况下也能获得良好的聚焦图像。文献[36]中朱小香将运动模型函数映射成线性,获得在谱域中达到的一个峰值,基于差分层析反演本身提出一个二维压缩感知(CS)为基础的方法——“SL1MMER”, 该方法在保持方位-距离向分辨率的同时获得高程-形变速率向的超分辨率,有良好的稳健性,不受旁瓣干扰的影响。
2016年,任笑真提出了一种基于幅度和相位迭代重建的四维合成孔径雷达成像方法[37],将四维合成孔径雷达高度-速率成像问题转化为目标复散射系数的幅度和相位联合重建问题,通过在成像过程中引入相位信息来改善成像质量,并验证了算法的有效性。2017年,王爱春、向茂生等考虑目标的稀疏特性和结构特性这两种特性,提出一种联合Khatri-Rao子空间与块稀疏压缩感知[38-40](khatri-rao subspace and block compressive sensing, KRS-BCS)的差分层析成像方法[41],并通过模拟仿真数据和Envisat卫星ASAR实测数据进行验证,结果得出KRS-BCS差分层析成像方法不仅保持了高分辨率,而且实现了结构稀疏信号目标的四维空间信息估计。
相比传统的傅里叶变换算法和空间谱估计算法,压缩感知算法可以在远小于奈奎斯特采样定理的条件下,用随机采样获取信号的离散样本,通过非线性重建算法完成信号重建,改善了成像效果。同时,国内外研究学者在压缩感知理论基础上,根据观测目标本身的结构特性提出改进方法,更好地实现了具有稀疏信号目标的四维空间信息估计。
3 差分层析SAR主要应用及发展趋势 3.1 城市动态形变监测城市建筑的形变监测是差分层析的重要应用领域之一,在城市中,高度向可以造成相位的差异,同时建筑物的沉降及热胀冷缩也能造成相位信息的变化,仅高度维成像不足以表达相位信息,需要获取高度-形变速率维的高度和形变信息。文献[42]在2009年首次将ERS实测数据应用于差分层析成像中,对1992—2001年间意大利Naple市进行形变监测,2010年,文献[43]利用ERS系统自1995—2000年间的43轨数据,对罗马市区的城市建筑进行了形变监测。文献[44]利用Envisat卫星ASAR数据集对日本千叶茂原区进行地表形变监测,并利用一等水准点和实时测量的GPS站点数据进行精度验证,两种试验方法保持了良好的一致性,而且形变速率整体偏差较小。2016年,文献[45]采用TerraSAR-X影像数据对香港建筑区进行形变监测。同年,文献[46]利用单视SAR成像的应用案例,对巴塞罗那城市地区50幅条带式TerraSAR-X图像提取形变信息。
近年来,我国城市化进程不断加快,社会经济高速发展,出现了越来越多的高层建筑及大型综合设施,密集建筑群的出现,导致城市地质环境的改变,增加了安全隐患,而差分层析SAR可以对城区进行长期持续形变监测,为城市沉降的监测和安全事故预警方面提供重要的决策依据,对国民经济建设和公共安全具有十分重要的意义。
3.2 森林覆盖研究森林地区的动态监测和森林结构信息提取也是差分层析的一个重要应用领域。2008年,文献[47]使用E-SAR系统P波段的机载数据对瑞典Remningstorp的森林地区进行了差分层析试验,由于观测数据少,成像结果不理想,却验证了差分层析在森林地区成像的能力。2011年,文献[48]利用E-SAR的多基线P波段数据,反演获取了Remningstorp森林高度,同时,利用半参数化差分层析处理器来区别冠层和地面散射体,通过对干扰地面散射的体散射进行去耦合,估算冠层下地面的沉降速度。2012年,文献[49]将层析在森林高度、生物量估计的应用扩展到差分层析中,基于非离散频谱的自适应匹配模型,将冠层与地面点的高度进行分离,尽管有少量稀疏离散值,但是获得的森林高度图与地面LiDAR方式获取的非常相近,并且相比层析方法分辨率得到了提高。
由于森林体散射机制对极化方式具有强依赖性,可以利用不同极化信道[50]获得SAR数据,提高成像散射体垂直位置估计的精度,因此将极化信息与差分层析技术结合,对获取森林高度信息、冠层地面下的沉降信息、提取森林结构信息、生物量估计等方面具有重要意义。
3.3 地下水位季节性变化监测2017年,文献[51]采用2011—2013年间的45幅条带模式获取的TerraSAR/TanDEM-X影像数据,对Angkor遗址表层土壤毫米级形变变化与结构失稳信息进行提取,通过分析得出地下水位和石头热膨胀的季节性波动变化,导致结构不稳定和腐烂加重,增加了古迹倒塌的风险。
差分层析结合温度信息获得地下水位季节性变化信息,可以有效预防地下水位变化对地面建筑结构稳定性造成的危害,规避坍塌危险的发生。
3.4 考古学应用如今,文化遗产的可持续性面临着来自自然界的挑战,例如,地质灾害和水土流失及人类活动(如城市化、资源开发和旅游),由此产生一些不可恢复的破坏。为了避免和预防这些现象,SAR遥感在文化遗产应用中起到了至关重要的作用。
2017年,文献[52]提出了层析SAR在干旱沙漠景观的地下成像应用,通过协同分析SAR数据的振幅和相位通道信息,验证了层析SAR用于探测浅埋考古遗迹的潜力,这一应用需要考虑掩埋考古遗迹的深度及层析SAR垂直向分辨率的能力,波长为L波段的通常可以探测到0~1.5 m,P波段可以进行更深度的地下成像。为了更好地进行风险监测与预防评估,文献[53]提出扩展的D-TomoSAR方法,结合TomoSAR的三维成像特点和PS-InSAR技术的长时间形变监测特点,利用2013年5月至2015年2月的26幅TerraSAR-X/TanDEM-X条带式观测数据,对南京市的古城墙(明朝时期)进行地面形变监测及结构稳定性监测,显示靠近玄武门附近的古城墙有抬升趋势。
微波SAR信号通过穿透植被和干细粒砂表面,可以检测出树冠层或沙面掩盖的考古遗迹,在景观考古学和文化遗产破坏程度的风险评估方面具有很大的潜力。
3.5 冰川应用2014年,文献[6]通过对高度形变速率域中连续散射体的重构,实现了地面表层的非刚性运动体散射速度剖面的反演,并通过试验模拟了冰川运动情况。
目前,差分层析SAR在冰川运动方向的应用尚处在起步阶段,这方面的研究较少,但是近年来全球气候变暖,导致冰川发生溶解和滑移,会对整个生态系统、农业生产乃至人类生活造成重大影响,积极开展冰川方向的研究,具有很大的应用潜力。
4 差分层析SAR技术展望差分层析SAR成像技术实现了四维信息的获取,但是实际应用中数据获取、成像算法等方面仍然存在大量的问题需要研究。以下给出了目前差分层析成像技术中的问题,并对其发展趋势进行了展望。
4.1 大气效应影响SAR数据是一系列时间序列的影像集,由SAR系统的卫星重访方式获得,获取过程中不可避免地受到大气变化或时间失相关因素带来的误差影响。为避免大气影响引入的误差,可以加入气象数据或采用永久散射体技术(permanent scatterer,PS)[54-55],PS技术建立在相干性很高的永久散射体上,可以很好地估计并去除大气效应。
4.2 高分辨率的成像算法差分层析四维成像是在层析SAR基础上,通过高度-速率二维聚焦成像。如何保持方位-距离向分辨率的同时保持高度-形变速率的高分辨率,是差分层析成像的一个难点问题。目前,差分层析成像技术的主要成像算法有:傅里叶变换算法、空间谱分析算法、压缩感知算法。其中压缩感知算法不受奈奎斯特定理的约束,可以实现较高分辨率的成像效果,是目前差分层析成像技术中最为有效的成像算法。由于实际目标在空间上的稀疏分布,因此针对目标本身特性,研究提出高分辨率成像算法是目前亟待解决的问题。
4.3 非线性形变问题在差分层析成像中,由于散射体的运动不均是线性,可能是热胀冷缩效应导致的非线性形变或其他形变,因此四维SAR层析成像不一定适用于所有情况。为避免目标非线性形变产生的误差,可以将四维模型扩展为多维模型。2011年,研究人员将四维SAR层析成像拓展到更多维,提出了一种3+M维SAR层析成像模型,通过重新排列采集的SAR数据,将任何非线性多分量运动转化为线性分量运动,通过将时间基线投影到人造时间基线,为“时间隧道”方法[56]提供了聚焦所需参数的可能性,使得差分层析扩展到(M+1)维[57]变形监测成为可能,具备非线性形变检测能力,可使其对在城市多维动态监测、预防地下水位变化等应用领域具有巨大发展潜力。
4.4 极化信息的应用多通道、全极化是未来SAR系统的发展趋势,多通道可以提供更加密集的数据,在抑制噪声提高成像能力方面具有优势,极化SAR对散射体的形状和方向具有敏感特性,将极化、多通道信息与差分层析结合,能够更全面地提取目标信息,对于监测冰川移动、森林垂直结构及冠层下森林地表沉降演变具有重大意义。
5 结语本文介绍了差分层析SAR成像的基本原理和处理流程,重点对差分层析成像的重构算法、国内外最新研究成果进行了综述,并总结了其在城市动态形变监测、地下水位季节性变化检测、考古学、冰川移动等领域的应用潜力;最后,指出了差分层析SAR成像技术的研究热点,对其未来的发展趋势进行了展望。随着多平台(卫星、飞机、地面)、SAR数据的批量获取,差分层析作为一个较新的四维信息获取方式,在地球环境因子定量反演过程中将会受到更多的关注。
| [1] | LOMBARDINI F. Differential tomography:a new frame-work for SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(1): 37–44. DOI:10.1109/TGRS.2004.838371 |
| [2] | ZHOU X, CHANG N B, LI S. Applications of SAR inter-ferometry in earth and environmental science research[J]. Sensors, 2009, 9(3): 1876–912. DOI:10.3390/s90301876 |
| [3] | ROSEN P A, HENSLEY S, JOUGHIN I R, et al. Synthetic aperture radar interferometry[J]. Proceedings of the IEEE, 2002, 88(3): 333–382. |
| [4] | VIVIANI F, PULELLA A, LOMBARDINI F. Multidi-mensional tomography with new generation VHR SAR data for urban monitoring[C]//Proceedings of 2013 IEEE International Geoscience and Remote Sensing Symposium. Melbourne, VIC: IEEE, 2014: 81-84. |
| [5] | LOMBARDINI F, VIVIANI F. New developments of 4D+differential SAR tomography to probe complex dynamic scenes[C]//Proceedings of 2014 IEEE Geoscience and Remote Sensing Symposium. Quebec City: IEEE, 2014: 3362-3365. |
| [6] | LOMBARDINI F, VIVIANI F. Multidimensional SAR tomography: advances for urban and prospects for forest/ice applications[C]//Proceeding of the 11th European Radar Conference.Rome: IEEE, 2014: 225-228. |
| [7] | LOMBARDINI F, TEBALDINI S. Multidimensional SAR tomography: methods and applications[C]//Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium. Fort Worth, TX: IEEE, 2017: 2460-2463. |
| [8] | LOMBARDINI F, VIVIANI F. Differential tomography applications to volumetric scatterers: simulated and real analyses for ice and forest scenarios[C]//Proceeding of the 10th European Conference on Synthetic Aperture Radar. Berlin: VDE, 2014: 1-4. |
| [9] | FORNARO G, LOMBARDINI F, SERASINO F. Multidi-mensional imaging with ERS data[C]//Proceedings of Fringe Workshop. Frascati: [s.n.], 2006. |
| [10] | 徐玲玲, 赵永芳, 井孝功. 狄拉克δ函数[J]. 大学物理, 2010, 29(8): 16–17. DOI:10.3969/j.issn.1000-0712.2010.08.003 |
| [11] | 曾琪明, 解学通. 基于谱运算的复相关函数法在干涉复图像配准中的应用[J]. 测绘学报, 2004, 33(2): 127–131. DOI:10.3321/j.issn:1001-1595.2004.02.007 |
| [12] | LIN Q, VESECKY J F, ZEBKER H A. New approaches in interferometric SAR data processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(3): 560–567. DOI:10.1109/36.142934 |
| [13] | 赵志伟, 杨汝良, 祁海明. 一种改进的星载干涉SAR复图像最大频谱配准算法[J]. 测绘学报, 2008, 37(1): 64–69. DOI:10.3321/j.issn:1001-1595.2008.01.012 |
| [14] | SERAFINO F. SAR image coregistration based on isolated point scatterers[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 354–358. DOI:10.1109/LGRS.2006.872399 |
| [15] | 王青松, 瞿继双, 黄海风, 等. 联合实、复相关函数的干涉SAR图像配准方法[J]. 测绘学报, 2012, 41(4): 563–569. |
| [16] | FORNARO G, LOMBARDINI F, SERAFINO F. Three-dimensional multipass SAR focusing:experiments with long-term spaceborne data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 702–714. DOI:10.1109/TGRS.2005.843567 |
| [17] | FORNARO G, SERAFINO F. Imaging of single and double scatterers in urban areas via SAR tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(12): 3497–3505. DOI:10.1109/TGRS.2006.881748 |
| [18] | 孙希龙, 余安喜, 杜海东, 等. 基于模拟干涉相位去斜的SAR层析处理方法[J]. 国防科技大学学报, 2011, 33(3): 105–110. DOI:10.3969/j.issn.1001-2486.2011.03.021 |
| [19] | COSTANTINI M, MINATIi F, PIETRANERA L. A curvature based method for combining multi-temporal SAR differential interferometric measurements[C]//Proceeding of Fringe Workshop. Frascati: [s.n.], 2004: 550. |
| [20] | ZHU X X, BAMLER R. Tomographic SAR inversion by L1-norm regularization:the compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839–3846. DOI:10.1109/TGRS.2010.2048117 |
| [21] | 孙希龙. SAR层析与差分层析成像技术研究[D].长沙: 国防科学技术大学, 2012. |
| [22] | REIGBER A, MOREIRA A. First demonstration of airborne SAR tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142–2152. DOI:10.1109/36.868873 |
| [23] | REN X Z, YANG R L. An inverse problem based approach for differential SAR tomography imaging[J]. Journal of Electronics and Information Technology, 2010, 32(3): 582–586. DOI:10.3724/SP.J.1146.2009.00259 |
| [24] | MISHALI M, ELDAR Y C. From theory to practice:sub-nyquist sampling of sparse wideband analog signals[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 4(2): 375–391. |
| [25] | SERAFINO F, SOLDOVIERI F, LOMBARDINI F, et al. Singular value decomposition applied to 4D SAR imaging[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium.[S. l.]: IEEE, 2005: 2701-2704. |
| [26] | ZHU X X, BAMLER R. Very high resolution spaceborne SAR tomography in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4296–4308. DOI:10.1109/TGRS.2010.2050487 |
| [27] | 孙希龙, 余安喜, 董臻, 等. 一种差分SAR层析高分辨成像方法[J]. 电子与信息学报, 2012, 34(2): 273–278. |
| [28] | DICKEY F M, DOERRY A W. Superresolution and synthetic aperture radar[J]. Office of Scientific and Technical Information Technical Reports, 2001. DOI:10.2172/782711 |
| [29] | WANG B, WANG Y, HONG W, et al. Simulation research of parametric methods for multi-baseline SAR tomography[C]//Proceedings of the 1st Asian and Pacific Conference on Synthetic Aperture Radar. Huangshan: IEEE, 2007: 203-206. |
| [30] | DONOHO D L. Compressed sensing[J]. IEEE Trans-actions on Information Theory, 2006, 52(4): 1289–1306. DOI:10.1109/TIT.2006.871582 |
| [31] | CANDES E J, TAO T. Near-optimal signal recovery from random projections:universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406–5425. DOI:10.1109/TIT.2006.885507 |
| [32] | ZHU X, BAMLER R, BAMLER R. Super-resolution for 4D SAR tomography via compressive sensing[C]//Proceedings of the 8th European Conference on Synthetic Aperture Radar. Aachen: VDE, 2011: 1-4. |
| [33] | 孙希龙, 余安喜, 董臻, 等. 基于压缩感知的星载SAR差分层析高分辨成像[J]. 信号处理, 2012, 28(5): 659–666. DOI:10.3969/j.issn.1003-0530.2012.05.007 |
| [34] | REN X Z, LI Y F, YANG R. Four-dimensional SAR imaging scheme based on compressive sensing[J]. Progress in Electromagnetics Research B, 2012, 39(39): 225–239. |
| [35] | REN X Z, CHEN L N. Four-dimensional SAR imaging algorithm using bayesian compressive sensing[J]. Journal of Electromagnetic Waves and Applications, 2014, 28(13): 1661–1676. DOI:10.1080/09205071.2014.938174 |
| [36] | ZHU X X, Bamler R. Compressive sensing for high resolution differential SAR tomography-the SL1MMER algorithm[C]//Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium. Honolulu, HI: IEEE, 2010: 17-20. |
| [37] | 任笑真, 杨汝良. 一种基于幅度和相位迭代重建的四维合成孔径雷达成像方法[J]. 雷达学报, 2016, 5(1): 65–71. |
| [38] | ELADR Y C, KUPPINGER P, BOLCSKEI H. Block-sparse signals:uncertainty relations and efficient recovery[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3042–3054. DOI:10.1109/TSP.2010.2044837 |
| [39] | SHERVASHIDZE N, BACH F. Learning the structure for structured sparsity[J]. IEEE Transactions on Signal Processing, 2015, 63(18): 4894–4902. DOI:10.1109/TSP.2015.2446432 |
| [40] | TERADA T, NISHIMURA T, OGAWA Y, et al. DOA estimation for multi-band signal sources using compressed sensing techniques with Khatri-rao processing[J]. Ieice Transactions on Communications, 2014, E97.B(10): 2110–2117. DOI:10.1587/transcom.E97.B.2110 |
| [41] | 王爱春, 向茂生, 汪丙南. 一种联合Khatri-Rao子空间与块稀疏压缩感知的差分SAR层析成像方法[J]. 电子与信息学报, 2017, 39(1): 95–102. |
| [42] | FORNARO G, SERAFINO F, Reale D. 4-D SAR imaging:the case study of rome[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(2): 236–240. DOI:10.1109/LGRS.2009.2032133 |
| [43] | FORNARO G, REALE D, SERAFINO F. Four-dimen-sional SAR imaging for height estimation and monitoring of single and double scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 224–237. DOI:10.1109/TGRS.2008.2000837 |
| [44] | 王爱春, 向茂生, 汪丙南. 城区地表形变差分TomoSAR监测方法[J]. 测绘学报, 2016, 45(12): 1413–1422. DOI:10.11947/j.AGCS.2016.20160113 |
| [45] | MA P, LIN H. Robust detection of single and double persistent scatterers in urban built environments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(4): 2124–2139. DOI:10.1109/TGRS.2015.2496193 |
| [46] | SIDDIQUE M A, WEGMULLER U, HAJNSEK I, et al. Single-look SAR tomography as an add-on to PSI for improved deformation analysis in urban areas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 6119–6137. DOI:10.1109/TGRS.2016.2581261 |
| [47] | LOMBARDINI F, FORNARO G, PARDINI M, et al. SAR tomography for scene elevation and deformation reconstruction: algorithms and potentialities[C]//Proceedings of 2008 IEEE Radar Conference. Rome: IEEE, 2008: 1-7. |
| [48] | CAI F, LOMBARDINI F, PASCULLI D, et al. Tomo and diff-tomo SAR methodologies: Recent advances for urban and forest applications[C]//Proceedings of the 3rd International Asia-Pacific Conference on Synthetic Aperture Radar. Seoul: IEEE, 2011: 1-3. |
| [49] | LOMBARDINI F, CAI F, VIVIANI F. Forest "dynamic" tomography: height-varying temporal coherence separation[C]//Proceedings of 2012 Tyrrhenian Workshop on Advances in Radar and Remote Sensing. Naples: IEEE, 2012: 94-99. |
| [50] | FREEMAN A, DURDEN S L. A Three-component scattering model for polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963–973. DOI:10.1109/36.673687 |
| [51] | CHEN F, GUO H, MA P, et al. Radar interferometry offers new insights into threats to the angkor site[J]. Science Advances, 2017, 3(3): e1601284. DOI:10.1126/sciadv.1601284 |
| [52] | CHEN F, YOU J, TANG P, et al. Unique performance of spaceborne SAR remote sensing in cultural heritage applications:overviews and perspectives[J]. Archaeological Prospection, 2018, 25(1): 71–79. DOI:10.1002/arp.1591 |
| [53] | CHEN F, WU Y, ZHANG Y, et al. Surface motion and structural instability monitoring of ming dynasty city walls by two-step tomo-PSInSAR approach in Nanjing city, China[J]. Remote Sensing, 2017, 9(4): 371. DOI:10.3390/rs9040371 |
| [54] | HILLEY G E, BÃ1/4RGMANN R, FERRETTI A, et al. Dynamics of slow-moving landslides from permanent scatterer analysis[J]. Science, 2004, 304(5679): 1952–1955. DOI:10.1126/science.1098821 |
| [55] | WANG S, GONG H, ZHAOFENG D U, et al. Optimal selection of master image in permanent scatterer InSAR technique[J]. Acta Geodaetica et Cartographica Sinica, 2013, 1: 87–93. |
| [56] | ZHU X X, BAMBER R. Let's do the time warp:multicomponent nonlinear motion estimation in differential SAR tomography[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 735–739. DOI:10.1109/LGRS.2010.2103298 |
| [57] | FORNARO G, REALE D, VERDE S. Bridge thermal dilation monitoring with millimeter sensitivity via multidimensional SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 10(4): 677–681. |



