2. 贵州大学矿业学院, 贵州 贵阳 550025
2. College of Mining, Guizhou University, Guiyang 550025, China
影像匹配的用途极为广泛,目前的研究热点主要集中在多视角倾斜航空影像的三维建模[1]、目标检测与跟踪[2]等方向。针对无人机遥感影像的匹配和拼接,部分学者开展了一定的研究,考虑AKAZE(accelerated KAZE)算法在构建非线性尺度空间时,能较为完整地保存影像纹理结构和局部信息[3-4],文献[5]提出把AKAZE算法和相位相关法结合在一起对纹理缺乏的地区影像进行匹配。该匹配方法初步解决了纹理缺乏地区的影像匹配问题。文献[6]提出一种快速有效的SIFT(scale invariant feature transform,SIFT)特征提取算法,该算法提取特征点的数量显著降低,较大程度提升了算法效率,但耗时情况还有待改善。文献[7]提出一种改进BRISK(binary robust invariant scalable key points,BRISK)特征的快速图像配准算法,该配准算法在保持速度的基础上达到亚像素级配准精度,并具有优越的场景适应性能。文献[8]针对小型无人机航拍图像视点离散、视角变化有一定运动规律的特点,结合Harris特征点和SIFT特征向量的优势,对SIFT算法进行了改进,试验证明了该改进算法在准确度和配准耗时等方面得到了较大的提高。由于SIFT算法的实时性较差,文献[9]首先提出了一种特征点检测算法(oriented fast and rotated BRIEF),该算法用FAST[10](features from accelerated segment test)来对影像提取特征点,其特征采用BRIEF[11](binary robust independent elementary features)来描述,该算法较大程度上降低了提取特征点的总耗时。文献[12]结合SIFT和RANSAC(RANdom sample consensus, RANSAC)[13-14]算法对InSAR影像配准,该方法可得到稳定、可靠的匹配点对,但运算速度还有待进一步提升。文献[15]基于SURF算法和极线约束条件对无人机影像进行匹配,试验证明了极线约束条件下的无人机影像匹配在误匹配减少的前提下能获得更多准确的特征匹配集。在分析上述算法优、缺点基础上,本文提出一种基于特征组合和RANSAC算法的无人机遥感影像匹配方法。AKAZE特征检测算法是KAZE[16]算法的改进算法,SIFT算法具有良好的尺度与旋转不变性[17],本文首先采用AKAZE提取影像特征点,然后利用SIFT算法描述特征向量和获得主方向,最后基于单映射变换矩阵的RANSAC算法进行精准匹配。针对无人机遥感影像匹配中提取特征点的时长、匹配正确率等指标,对基于特征组合、AKAZE、SIFT和BRISK这4种算法的无人机遥感影像匹配进行试验对比分析,验证基于特征组合与RANSAC算法的匹配方法在无人机遥感影像匹配上的可行性。
1 特征组合检测算法本文的特征组合检测算法提取特征点步骤如下:
(1) 利用AOS算法和可变传导函数建立非线性尺度空间,然后进行尺度归一化,得到AKAZE特征点。
(2) 利用SIFT算法描述特征向量,获得特征点的主方向。
1.1 AKAZE特征点检测 1.1.1 非线性扩散滤波非线性扩散滤波:在不同尺度上变化的影像亮度记为L,将其表达为某一关系的流动函数的散度,数学表达式如下
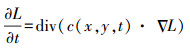 (1)
(1) 选取的传导函数c(x, y, t)如果合适,则可得到扩散自适应于图像的局部结构。t为尺度参数,影像的表达形式复杂程度随着t值的增大而减小。传导函数的数学表达式为
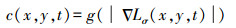 (2)
(2) 式中,ΔLσ为高斯平滑后图像的梯度。其中g()的函数在文献[3]中有详细描述,本文不再细述。
1.1.2 AOS算法因为非线性偏微分方程无直接解,本文采用隐式差分来进行求解。本文隐式差分利用的数学形式为
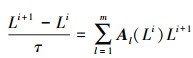 (3)
(3) 式中,Al为影像在各维度(l)上传导性矩阵。此方程的数学形式解为
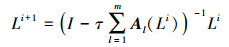 (4)
(4) 式中,Al为对角占优的三对角矩阵;步长(τ)可以任意取值,并利用Thomas算法加速求解。
1.1.3 非线性尺度空间的构造非线性尺度空间构造方法为:尺度级别成对数递增,存在M组octaves,各个octave又存在P个sub-level。AKAZE每一个层级利用的分辨率和最初的图像一致。M组octave与P个sub-level在本文中分别记作m和p,尺度参数σ通过下式与m和p互匹配
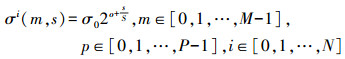 (5)
(5) 式中,σ0为给定的初始值;N为尺度空间的影像总数,N=M×P。式(6)将σi(单位为像素)转变为ti(进化时间)
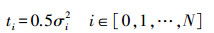 (6)
(6) 影像处理过程中,用高斯滤波预处理AKAZE特征检测算法,然后获得处理影像的梯度直方图,进而可得到对比度参数。采用AOS算法,并依据一组进化时间,来完成非线性尺度空间的构建,其数学表达式为
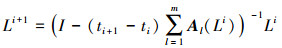 (7)
(7) 采用搜索不同尺度归一化后获得的Hessian局部极大值点。Hessian矩阵可由下式得到
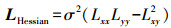 (8)
(8) 式中,将尺度参数σi取整得到σ。为了获得极值点,将所有像素点与它周围的全部相邻像素点相比,将中心像素点和周围26个相邻点比较。确定特征点所在位置后,继续进行亚像素精准定位,该方法的泰勒展开表达式为
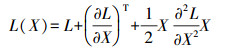 (9)
(9) 特征点的亚像素坐标的解为
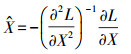 (10)
(10) (1) 当特征点的位置确定后,在特征点所在的尺度获取邻域,把该邻域均分为36个方向计算直方图,获得的直方图中最大值对应的方向就是特征点的主方向。
(2) 对计算所得直方图峰值而言,与最大直方图峰值相比,如该峰值所占比例达到最大直方图峰值的80%以上,则把此方向视作辅方向。约有1/5的特征点会存在一个甚至更多的辅方向,并且这些特征点在匹配中起到非常重要的作用,辅方向极容易影响匹配过程的稳定性。
1.2.2 计算特征点描述子要想获得具有较强独立性的描述子,确保组合特征检测算法的匹配正确率,需满足以下几个条件:①还需校正已得到的主方向;②利用校正后的主方向生成描述子,进而得到128维的特征向量;③需对特征向量进行归一化处理,减弱光照对匹配率的影像。
2 单映射变换矩阵的RANSAC精匹配随机抽样一致性算法是在一组存在“外点”的数据集里面,寻找一个符合该模型最佳的单映射变换矩阵H(8个未知参数,至少存在4组匹配点对),采用寻找到的最优矩阵来满足特征点数量最多。
文中基于单映射变换矩阵的RANSAC算法进行精匹配的具体步骤如下:
(1) 从特征组合算法提取的特征匹配点对中任意取出4个样本,并保证这4个样本之间不共线,利用RANSAC算法,计算出H矩阵,记为模型Q。
(2) 将模型Q应用于全部数据集,计算符合该模型的点数和投影误差,若误差小于阈值ε,则对应的代价函数最小,此匹配点加入内点集,计算公式如下
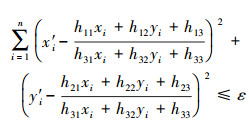 (11)
(11) 式中,(x′, y′)为原影像角点坐标。
(3) 任意取4组匹配点对,不断地进行步骤(1)、(2)的重复计算。
(4) 若通过以上步骤所得的内点集元素个数多于最优内点集,则把目前元素集视为最优内点集。当迭代次数不小于k时,可得到目标影像和待匹配影像之间的透视变换模型,把不满足此模型的点对删除,进而提高影像的匹配正确率。
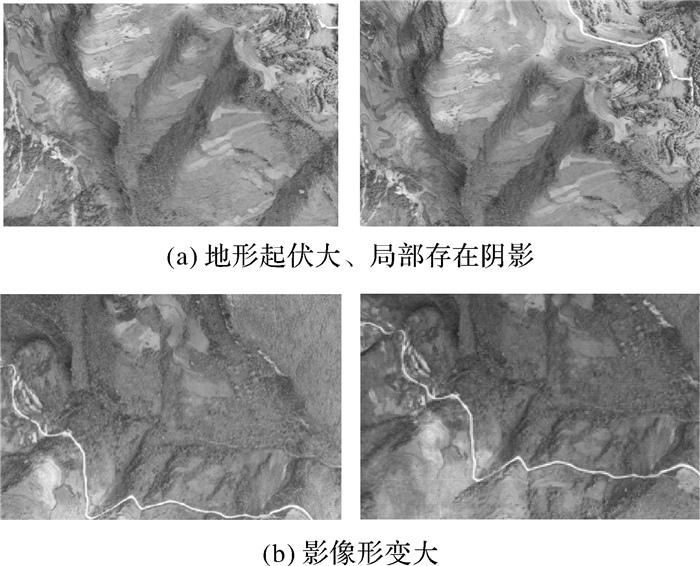
3 试验结果及分析为了验证本文方法在无人机遥感影像的匹配正确率及速度上的优势,试验利用4种算法对分辨率为580×387像素、640×426像素的两组遥感影像数据进行试验及对比分析,分析试验耗时情况及匹配精度。本次试验运行环境为:运行内存8 GB,AMD FX(tm)-8300 Eight-Core Processor 3.30 GHz的工作站,基于VS2015的Open-CV3.4.0计算机视觉库,Win10系统作为开发平台。试验所用的无人机遥感影像如图 1所示,分别为影像对(a)、(b),影像对(a)地形起伏大、局部存在阴影,影像对(b)影像变形大。
|
| 图 1 试验影像 |
试验结果对比分析如下:
(1) 表 1为特征组合、AKAZE、SIFT、BRISK这4种算法分别对(a)、(b)影像对的特征点提取数及耗时时长的试验结果。
| (特征点数/ms) | |||||
| 影像对 | 特征组合 | AKAZE | SIFT | BRISK | |
| (a) | 左 | 366/1 657.0 | 366/970.1 | 1593/2 153.2 | 2960/247.9 |
| 右 | 521/2 359.0 | 521/1 380.1 | 1778/2 404.1 | 3608/302.1 | |
| (b) | 左 | 342/1 899.7 | 342/1 137.9 | 1806/2 545.6 | 4370/320.6 |
| 右 | 390/2 166.3 | 390/1 525.1 | 1755/2 473.4 | 4355/318.1 | |
由表 1可看出,对于影像对(a)而言,AKAZE算法提取的特征点数约为SIFT算法提取的特征点数的25%,为BRISK算法提取的特征点数的12%,AKAZE+SIFT的特征组合算法提取的特征点数和AKAZE算法的提取数量相等。从耗时情况来看,特征组合算法的提取耗时高于AKAZE算法,低于SIFT算法,但仍然高于BRISK算法。对于影像对(b)而言,AKAZE算法提取的特征点数约为SIFT算法提取的特征点数的20%,约为BRISK算法提取的特征点数的8%,AKAZE+SIFT的特征组合算法提取的特征点数和AKAZE算法的提取数量相等,特征点提取耗时介于AKAZE算法和SIFT算法之间,仍高于BRISK算法。究其原因,是由于AKAZE算法在构建非线性尺度空间时耗时较多造成的。
(2) 本研究分别对影像对(a)、(b)采用特征组合检测算法、AKAZE、SURF和BRISK算法进行特征点检测试验,并利用基于单映射变换矩阵的RANSAC算法删除误匹配点对。由于篇幅限制,本文只列出特征组合+RANSAC算法的匹配效果图。

|
| 图 2 特征组合处理影像对(a)精匹配效果 |

|
| 图 3 特征组合处理影像对(b)精匹配效果 |
| 影像 | 特征组合 | AKAZE | SIFT | BRISK | |||||||
| (共匹配点对/时间)/(个/ms) | 匹配正确率/(%) | (共匹配点对/时间)/(个/ms) | 匹配正确率/(%) | (共匹配点对/时间)/(个/ms) | 匹配正确率/(%) | (共匹配点对/时间)/(个/ms) | 匹配正确率/(%) | ||||
| (a) | 156/4368 | 95 | 128/3520 | 84 | 160/6155 | 80 | 120/15 842 | 81 | |||
| (b) | 142/4331 | 88 | 117/3442 | 92 | 159/6516 | 82 | 150/21 637 | 84 | |||
(1) 对于地形起伏大、局部存在阴影的影像对(a),就匹配总耗时而言,特征组合的总耗时高于AKAZE算法,低于SIFT算法且远低于BRISK算法的总耗时,约为BRISK算法耗时的30%,说明特征组合检测算法在匹配速度上较好地继承了AKAZE算法的快速匹配性能。就匹配正确率而言,特征组合的匹配正确率为95%,均高于另外3种算法。特征组合、AKAZE、SIFT和BRISK这4种算法的正确匹配点对分别是156、128、160和120,可以看出特征组合后的正确匹配点对高于AKAZE算法和BRISK算法,接近于SIFT算法。
(2) 对于影像变形大的影像对(b),就匹配总耗时而言,特征组合的总耗时情况仍然介于AKAZE和SIFT算法之间,远低于BRISK算法的总耗时,约为BRISK算法的19%。就匹配正确率而言,特征组合、AKAZE、SIFT和BRISK这4种算法分别为88%、92%、82%和84%,可以看出特征组合检测算法的匹配正确率略低于AKAZE算法,高于另外两种算法。就正确匹配点对而言,特征组合的正确匹配点对多于AKAZE算法,略低于SIFT和BRISK算法。综合分析试验结果,基于特征组合与RANSAC算法的无人机遥感影像匹配方法在满足匹配正确率与正确匹配点对的前提下,其匹配耗时更短。考虑到后续工作是对多张无人机遥感影像进行匹配,当需匹配的无人机遥感影像数量众多时,该匹配方法更有利于无人机遥感影像的匹配。
4 结语无人机遥感影像匹配是无人机遥感影像拼接和三维重建的核心工作。从本文基于特征组合与RANSAC算法的无人机遥感影像匹配方法的试验结果可以看出:特征组合算法具有匹配速度快和冗余计算量少的优点。对于无人机遥感影像的匹配效果而言,本文提出的匹配方法从整体上优于AKAZE算法、SIFT算法和BRISK算法。与常用匹配方法相比,本文的匹配方法更加有效和快速,更适合于无人机遥感影像匹配。
| [1] | 关丽, 丁燕杰, 张辉, 等. 面向数字城市建设的三维建模关键技术研究与应用[J]. 测绘通报, 2017(2): 90–94. |
| [2] | 焦金龙, 卢小平. 顾及道路约束条件的动态目标检测与跟踪方法[J]. 测绘通报, 2017(5): 47–50. |
| [3] | 李鹏, 武文波, 王宗伟. 基于非线性尺度空间的多源遥感影像匹配[J]. 测绘科学, 2015, 40(7): 41–44. |
| [4] | 覃兵, 田军, 查宇飞, 等. 利用二值描述符的实时目标跟踪算法[J]. 西安电子科技大学学报, 2015, 42(5): 168–174. DOI:10.3969/j.issn.1001-2400.2015.05.028 |
| [5] | 王瑞瑞, 冯伍法, 张艳, 等. 一种结合相位相关法和AKAZE算法的纹理缺乏地区影像匹配技术[J]. 测绘通报, 2017(4): 49–52. |
| [6] | 牛俊伟, 郝向阳, 刘松林. 一种改进的SIFT特征提取算法[J]. 测绘科学技术学报, 2014, 31(2): 173–176. DOI:10.3969/j.issn.1673-6338.2014.02.015 |
| [7] | 何林阳, 刘晶红, 李刚, 等. 改进BRISK特征的快速图像配准算法[J]. 红外与激光工程, 2014, 43(8): 2722–2727. DOI:10.3969/j.issn.1007-2276.2014.08.055 |
| [8] | 熊自明, 万刚, 闫鹤, 等. 改进SIFT算法的小型无人机航拍图像自动配准[J]. 测绘科学技术学报, 2012, 29(2): 153–156. DOI:10.3969/j.issn.1673-6338.2012.02.018 |
| [9] | RUBLEE E, RABAUD V, KONOLIGE K, et al.ORB: an efficient alternative to SIFT or SURF[C]//Proceedings of the 2001 International Conference on Computer Vision.Barcelona: IEEE, 2011. |
| [10] | ROSTEN E, PORTER R, DRUMMOND T. Faster and better:a machine learning approach to corner detection[J]. IEEE Transactions on Pattern Analysis Machine Intelligence, 2010, 32(1): 105–119. DOI:10.1109/TPAMI.2008.275 |
| [11] | CALONDER M, LEPETIT V, FUA P.Brief: Binary robust independent elementary features[C]//Computer Vision ECCV 2010. Berlin: Springer, 2010: 778-792. |
| [12] | 陈华, 邓喀中, 张以文, 等. 结合SIFT和RANSAC算法的InSAR影像配准[J]. 测绘通报, 2015(12): 30–33. |
| [13] | 卜范秋, 宋伟东, 王伟玺. 一种针对近景影像的匹配算法[J]. 测绘科学, 2013, 38(6): 143–146. |
| [14] | 程德强, 厉航, 黄晓丽, 等. 基于改进随机抽样一致算法的视频拼接算法[J]. 工矿自动化, 2017, 43(8): 50–55. |
| [15] | 邓仕雄, 王晓红, 刘继庚, 等. 基于SURF算法和极限约束的无人机影像匹配研究[J]. 贵州大学学报(自然科学版), 2018, 35(1): 35–39. |
| [16] | 任克强, 胡梦云, 喻玲娟. 基于KAZE的自适应模糊图像配准算法[J]. 电子测量与仪器学报, 2017, 31(4): 559–565. |
| [17] | 贾丰蔓, 康志忠, 于鹏. 影像同名点匹配的SIFT算法与贝叶斯抽样一致性检验[J]. 测绘学报, 2013, 42(6): 877–883. |


